局部均值分解和排列熵在行星齒輪箱故障診斷中的應用

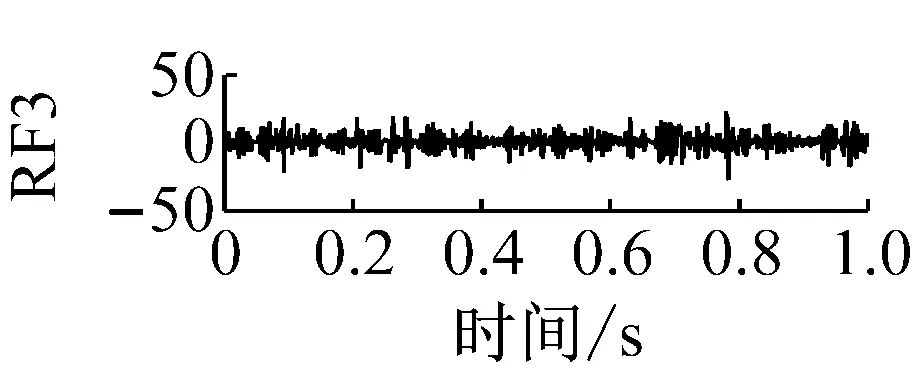
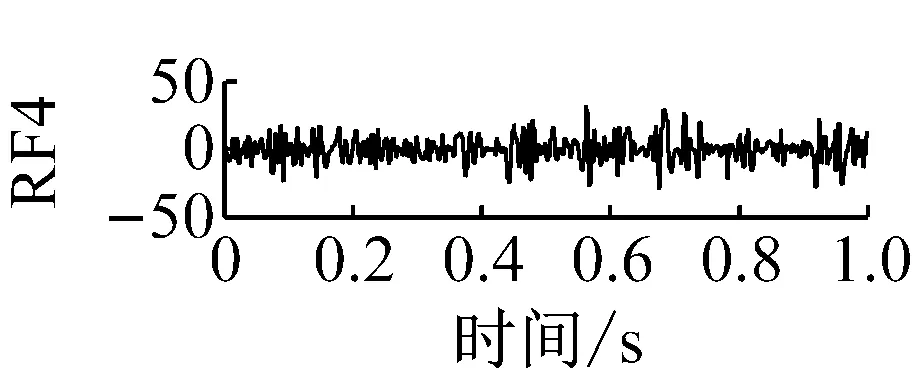
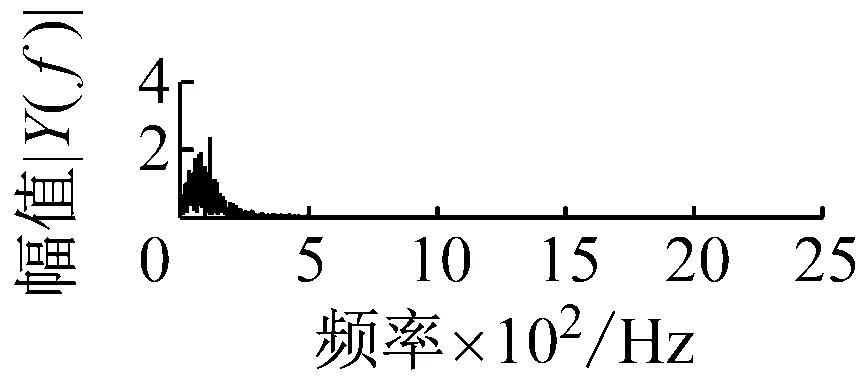
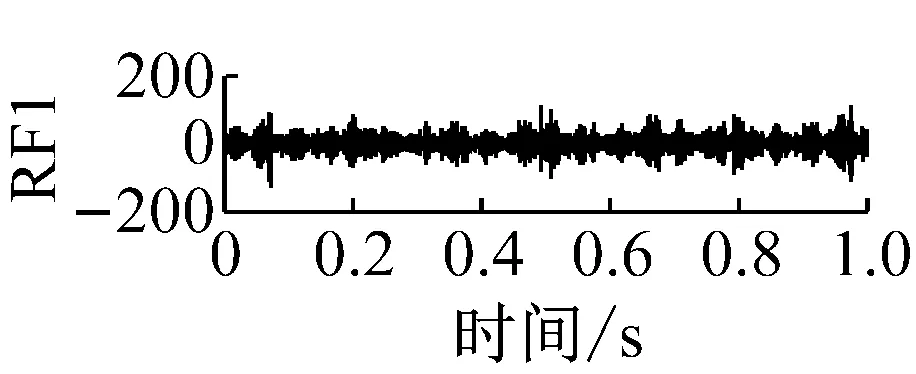
丁 闖, 張兵志, 馮輔周, 江鵬程

(裝甲兵工程學院 機械工程系，北京 100072)

局部均值分解和排列熵在行星齒輪箱故障診斷中的應用

丁 闖, 張兵志, 馮輔周, 江鵬程

(裝甲兵工程學院 機械工程系，北京 100072)

目前行星齒輪箱已經在軍用和民用裝備中廣泛應用，研究行星齒輪箱的故障診斷方法意義重大。針對行星齒輪箱在運行時產生的非線性非平穩振動，且故障特征信號微弱等問題，提出一種結合局部均值分解和排列熵的行星齒輪箱故障診斷方法。利用局部均值分解方法將不同狀態下的振動信號分解為多個乘積函數分量，針對包含有故障信息的分量進行排列熵計算，以此判斷故障類型。最后通過采集行星齒輪箱故障模擬試驗臺三種狀態(齒輪正常、太陽輪裂紋故障及行星輪裂紋故障)的振動信號，對其進行局部均值分解和排列熵計算，驗證了此方法的有效性。

行星齒輪箱；LMD；排列熵；故障診斷

由于行星傳動具有重量輕、體積小、傳動比大、承載能力強、傳動效率高等諸多優點，因此已被廣泛應用于作戰飛機、艦船、裝甲車輛、自行火炮及風力發電和工程機械等軍用裝備和民用裝備中[1]。由于行星齒輪箱結構復雜，不僅承受重載負荷，且運行工況復雜多變，在實際使用過程中，齒輪箱中的太陽輪、行星輪和齒圈、行星架等關鍵部件容易出現故障[2]。例如，我國某型主戰坦克使用的多檔位行星變速箱，共有三個行星排，結構非常復雜，使用條件異常惡劣，變速箱在使用過程中經常出現齒輪嚴重磨損、裂紋、斷齒等機械故障，如果故障不能及時被發現并排除，將嚴重影響主戰坦克的機動性能，導致戰斗力下降，并造成變速箱的二次損傷，使維修費用大幅提高。

目前，國內外學者對定軸齒輪箱故障診斷進行了深入的研究，提出了一系列卓有成效的診斷方法，取得了豐碩的成果。然而行星齒輪箱的結構不同于定軸齒輪箱，一般由太陽輪、多個行星輪、齒圈、行星架等組成，通常齒圈固定，太陽輪繞中心軸旋轉，而行星輪不僅繞各自中心軸自轉，同時繞太陽輪中心軸公轉，行星排結構如圖1所示，行星齒輪箱的復雜結構決定了其振動響應比定軸齒輪箱更加復雜，并存在明顯的非線性、非平穩性，且故障響應微弱。目前對于行星齒輪箱的故障診斷研究較少，應用尚不成熟。

近年來，排列熵算法的發展為行星齒輪箱的故障診斷提供了思路。行星齒輪箱在不同狀態運行時，其振動規律將發生變化，而排列熵算法可準確計算這一變化。為了定量描述行星齒輪箱不同運行狀態時振動規律的變化并識別其故障，本文提出一種結合局部均值分解(Local Mean Decomposition，LMD)和排列熵(Permutation Entropy，PE)的行星齒輪箱故障診斷方法。首先利用LMD方法分解行星齒輪箱的振動信號得到多個乘積函數分量(Product Function，PF)，并通過傅里葉變換求出每個PF分量包含的頻率成分，找出含有故障信息的PF分量，然后計算此分量的排列熵，通過得到的排列熵值判斷行星齒輪箱的工作狀態和故障類型[3-4]，基于LMD和排列熵的行星齒輪箱故障診斷流程如圖2所示。本文通過對齒輪正常、太陽輪裂紋及行星輪裂紋三種狀態的振動信號進行分析說明了此方法的有效性。

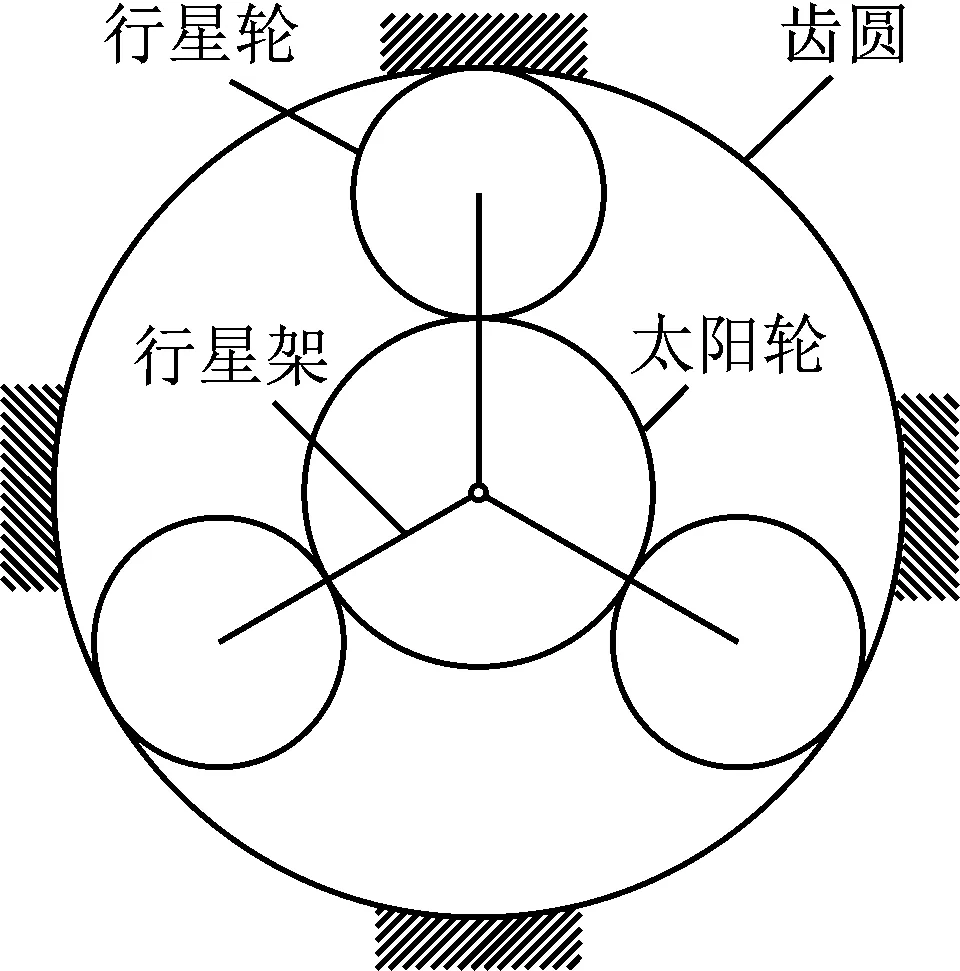
圖1 行星排結構

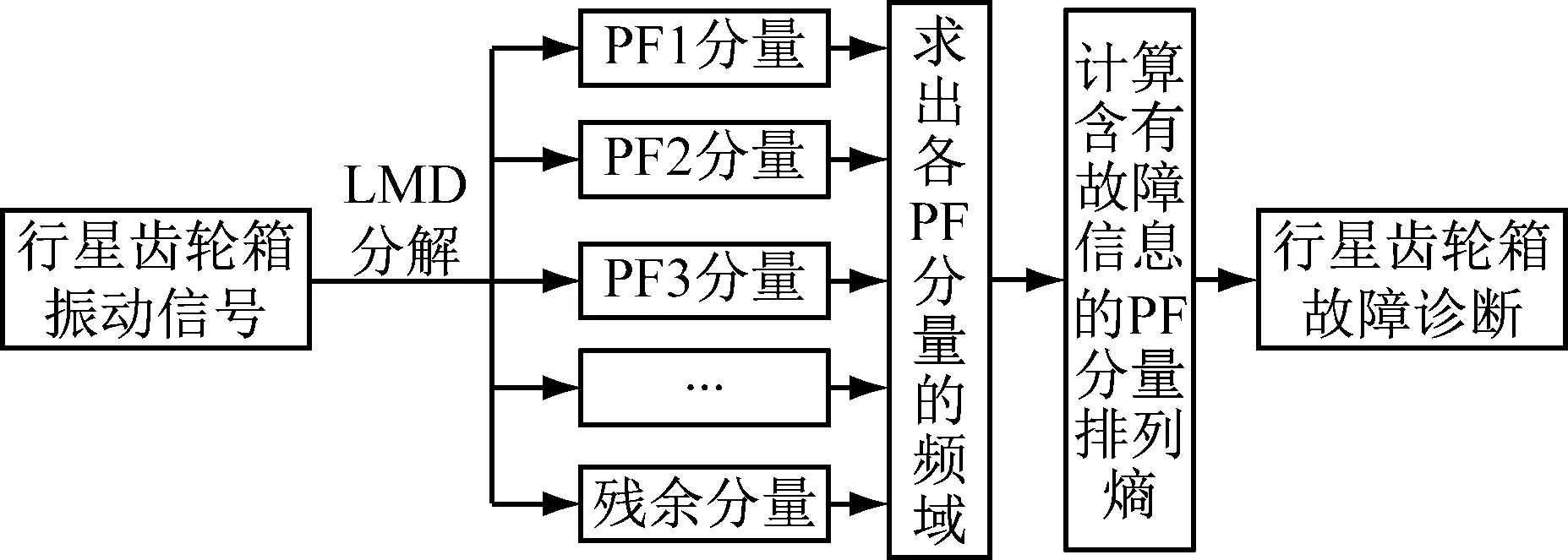
圖2 LMD和排列熵故障診斷流程圖

1 LMD原理

局部均值分解能自適應地將一個復雜信號分解成若干個瞬時頻率具有物理意義的PF分量之和，且非常適合非線性和非平穩信號[5]。LMD方法能夠克服小波分析及EMD存在的不足，且計算過程簡單，迭代次數少。而小波分析因小波基有限存在能量泄漏，EMD存在模式混淆、端點效應等問題，這些問題的存在都將造成的分析結果不準確。

LMD得到的每一個分量由一個包絡信號和一個純調頻信號相乘得到，包絡信號即為該PF分量的瞬時幅值，而該PF分量的瞬時頻率可由純調頻信號直接求出，LMD方法的計算流程如圖3所示，詳細分解過程見參考文獻[6]。

2 排列熵算法

“熵”的概念最早被Shannon用于描述信息論中信息的不確定性，同時給出了信息熵的數學表達式，定義一個不確定的概率分布的信息熵為

(1)

式(1)中k為常數，信息熵的大小可定量描述概率系統的平均不確定程度。根據這一理論，最不確定的概率分布具有最大的熵值，即反映了信息其概率分布的均勻性。

根據信息熵理論的定義，Bandt等[7-9]提出了排列熵的概念，排列熵是用于衡量一維時間序列復雜度的平均熵參數，其對信號變化具有很高的敏感性，能夠有效放大系統的微變信號，同時可以很好地檢測出復雜系統的動力學突變，且該方法具有計算過程簡單、抗噪聲能力強等特點，因此排列熵對于非線性、非平穩性的振動信號具有很好的檢測效果。由于排列熵自身的諸多優點使其在氣象預測、醫學等領域取得了廣泛的應用，也逐漸擴展至了機械故障診斷方面[10-11]。

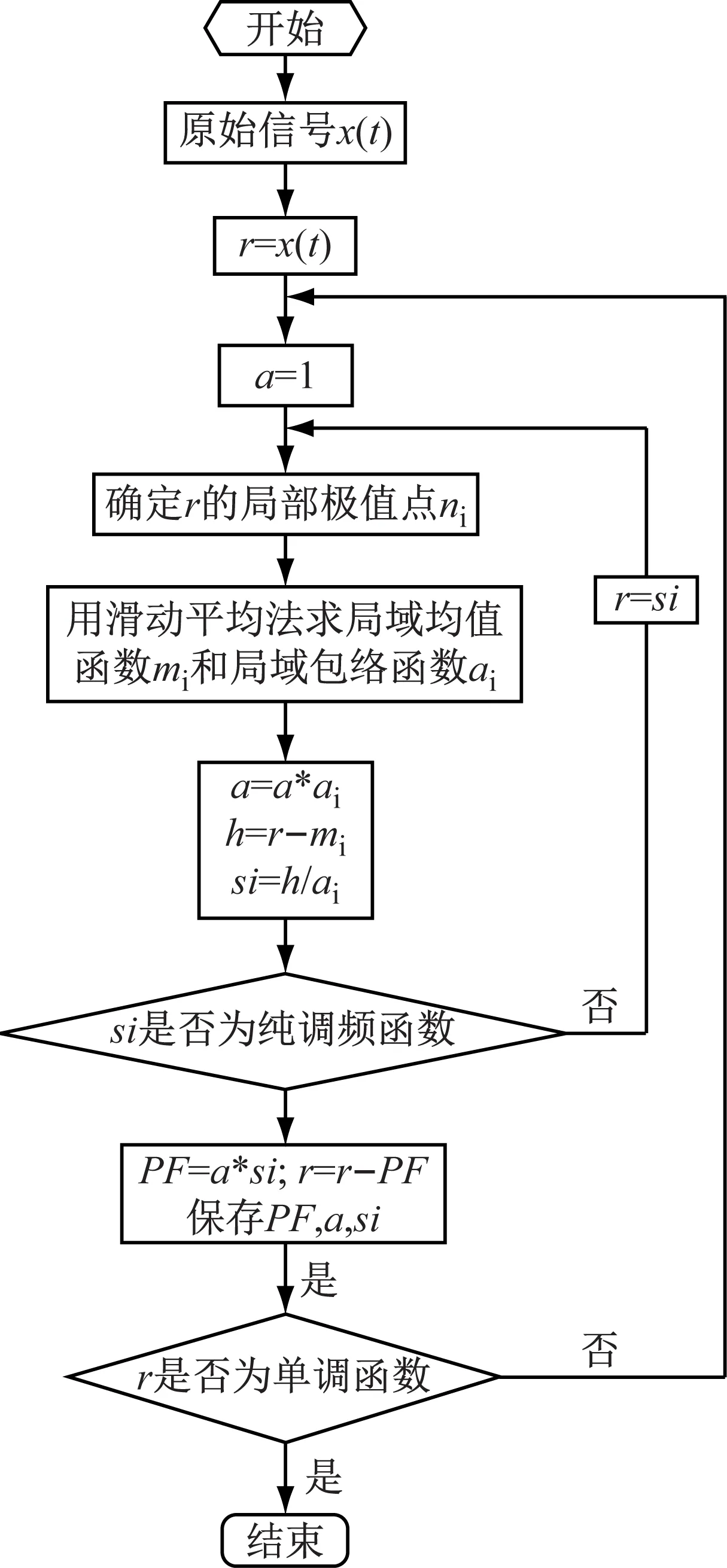
圖3 LMD方法的計算流程

排列熵的基本原理如下：

(1)相空間重構

假設有一時間序列X={x(i),i=1,2,3,…,n}，對此序列進行相空間重構，得到重構矩陣Y：

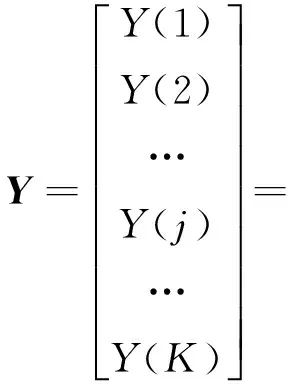
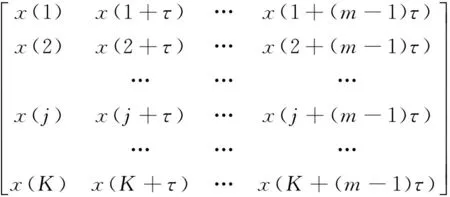
(2)

式中：j=1,2,3,…,K,m為嵌入維數，τ為延遲時間，K+(m-1)τ=n。重構矩陣中的每一行Y(j)為一個重構分量，重構矩陣中共有K個重構分量。

(2)升序排列

將重構矩陣Y中的第j個重構分量Y(j)={x(j)x(j+τ) …x(j+(m-1)τ)}按照升序重新排列，i1i2…im表示重構分量中各個元素所在列的位置索引，即:

x(j+(i1-1)τ)≤x(j+(i2-1)τ)≤…≤

x(j+(im-1)τ)

(3)

若重構分量中存在相等的值，即

x(j-(ip-1)τ)=x(j-(iq-1)τ)

(4)

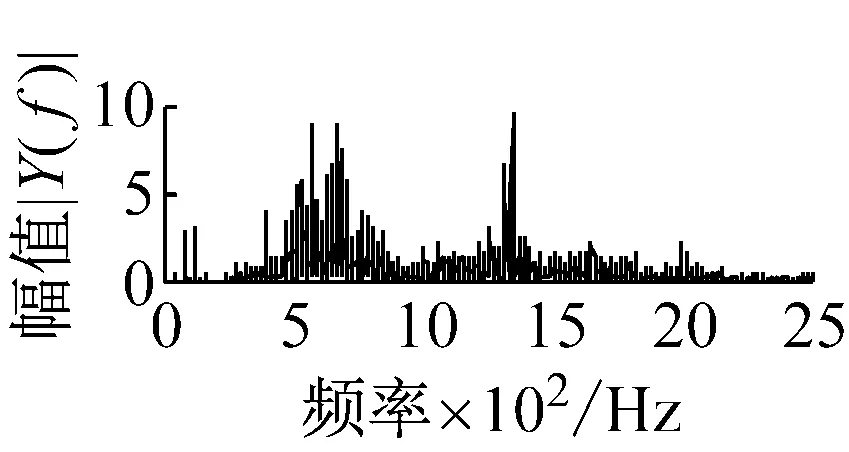
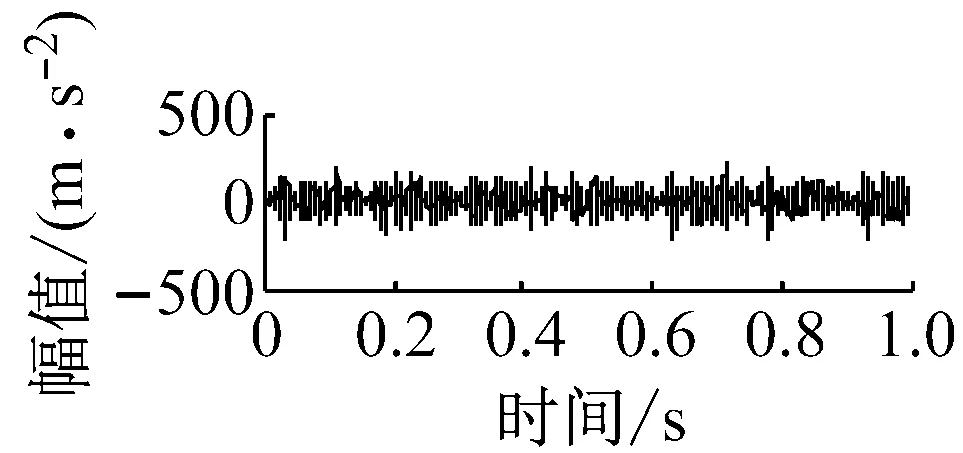
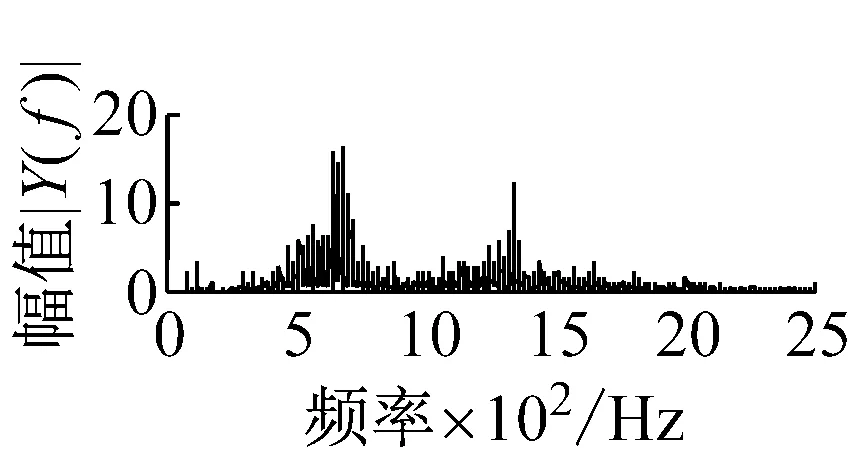
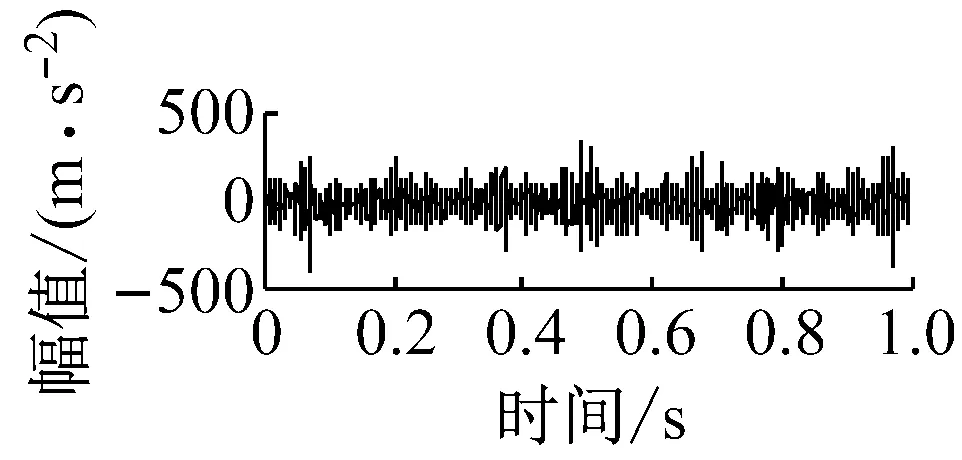
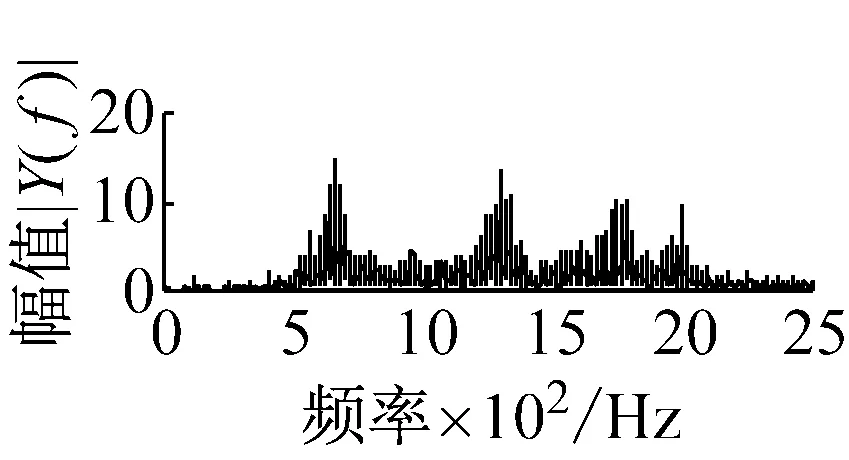
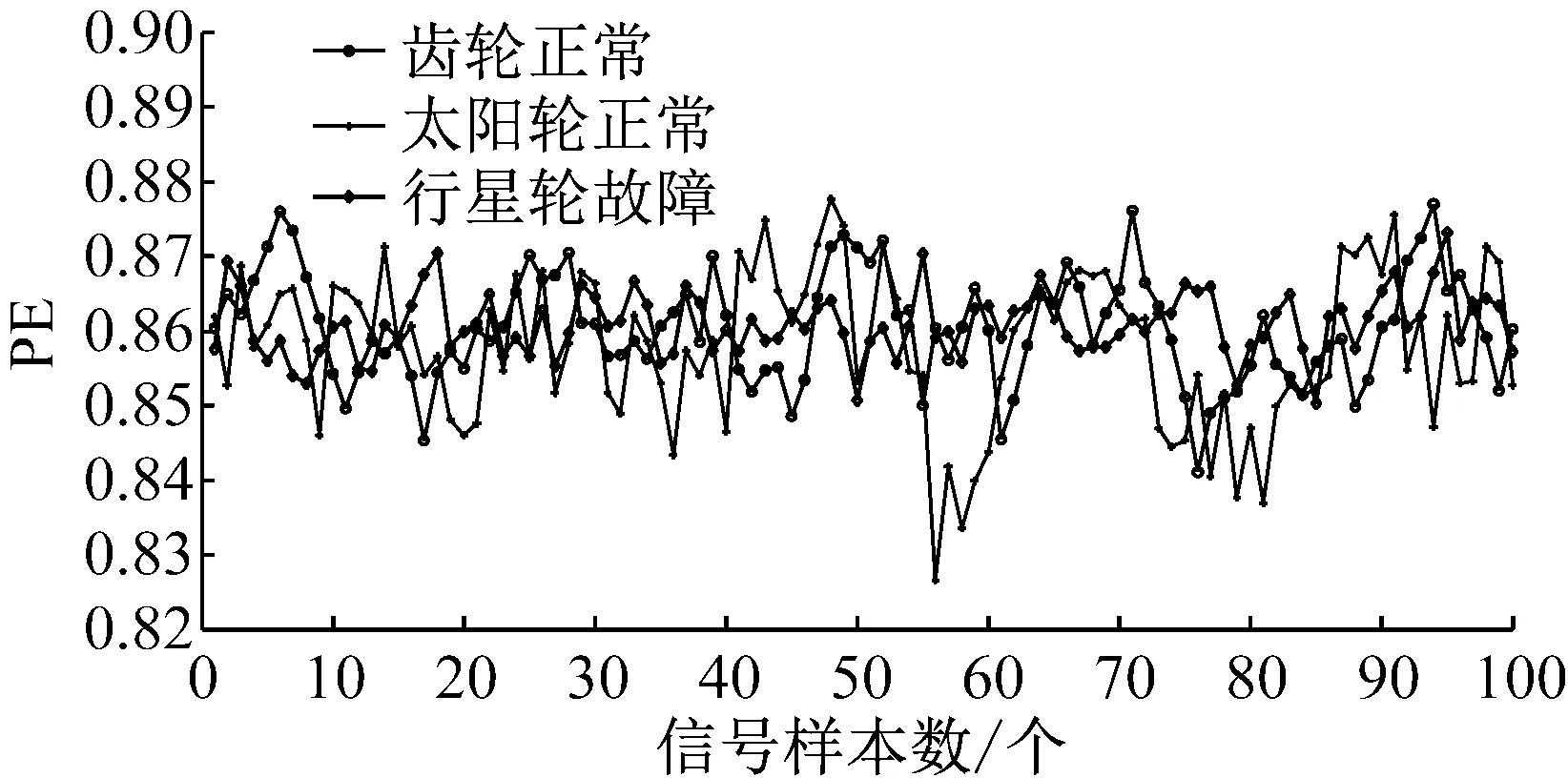
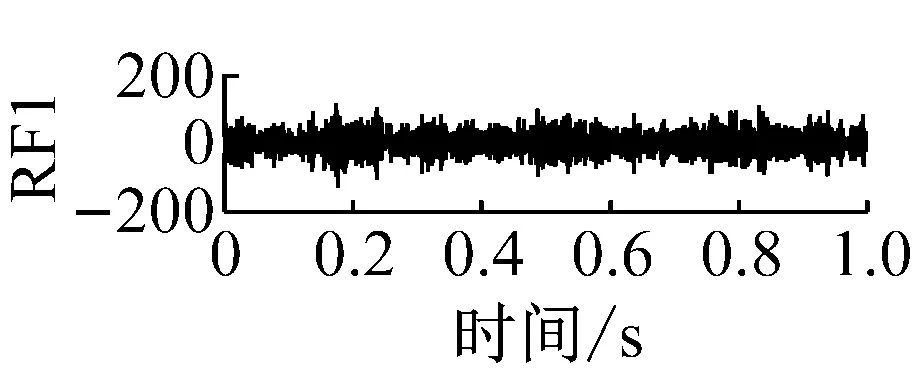
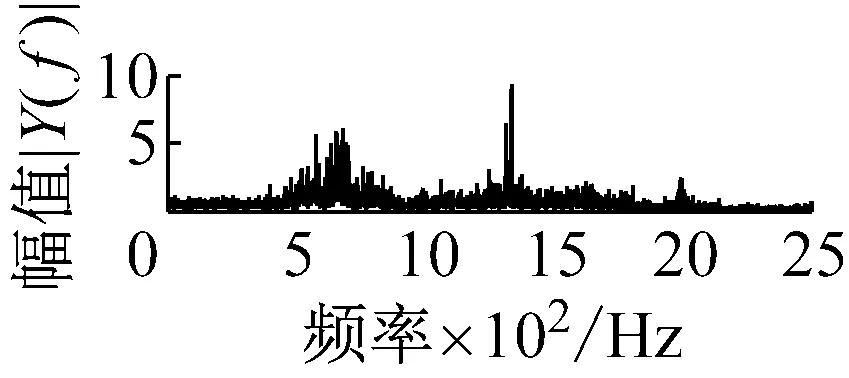
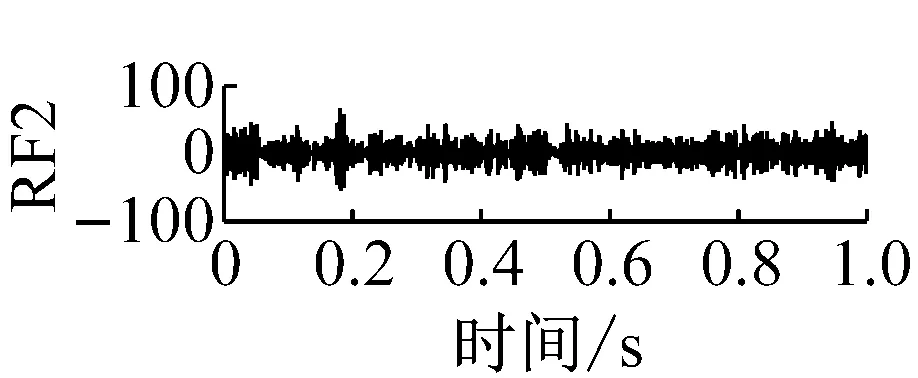
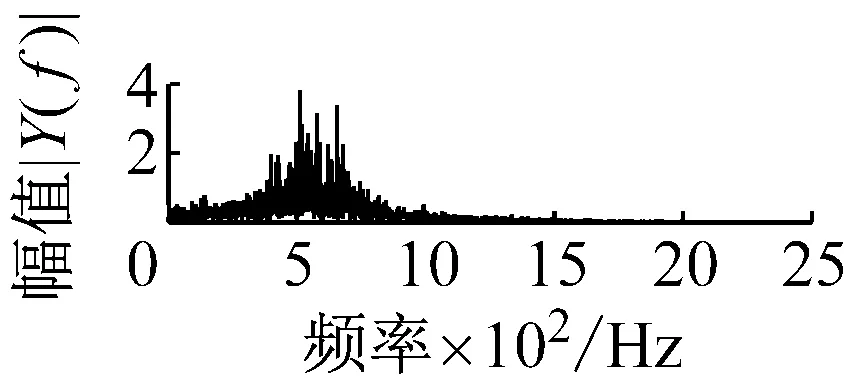
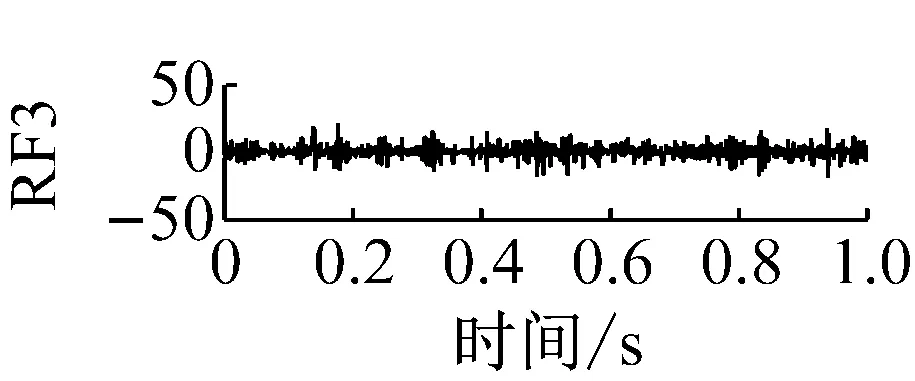
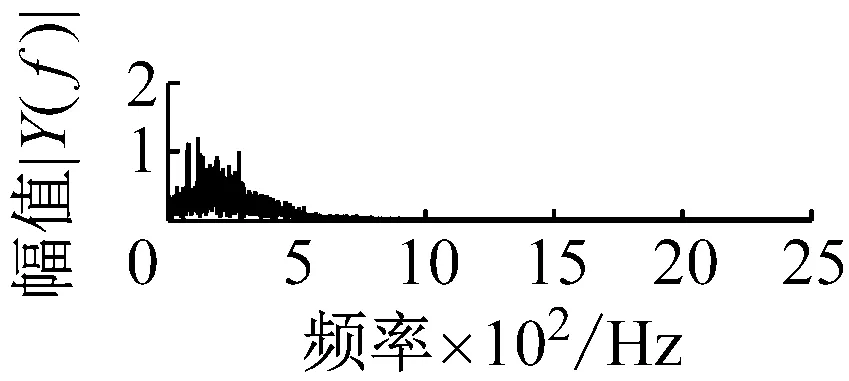
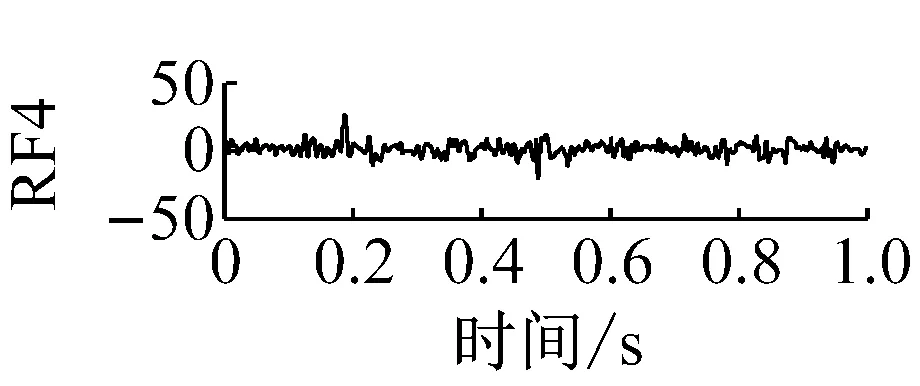
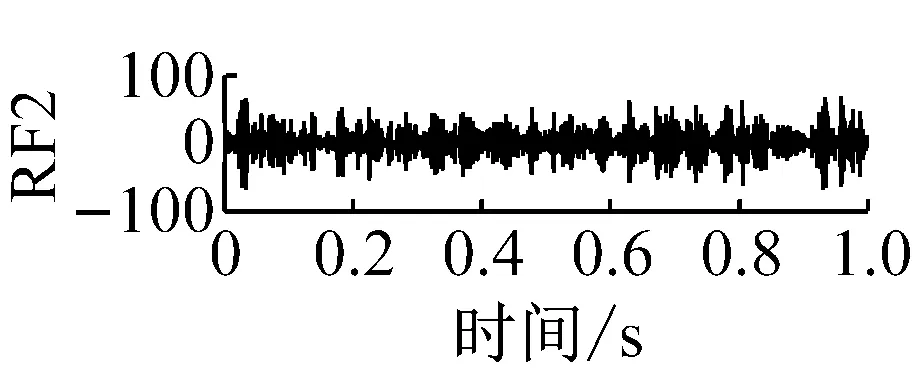
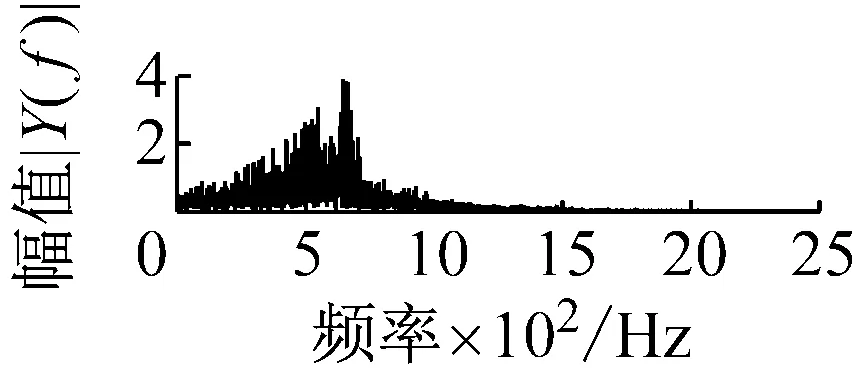
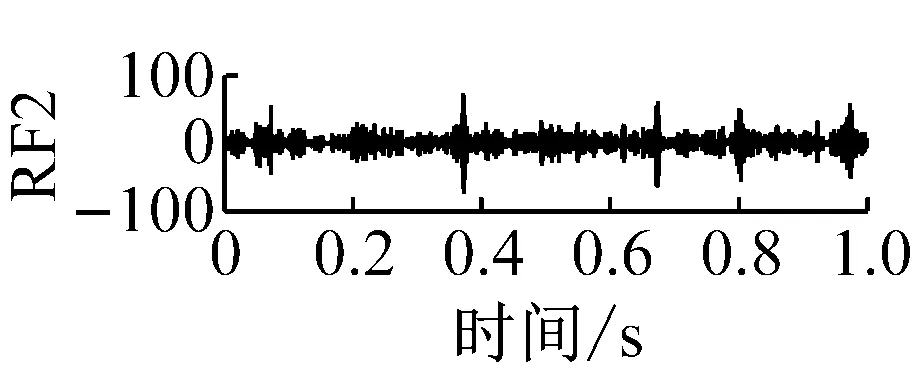
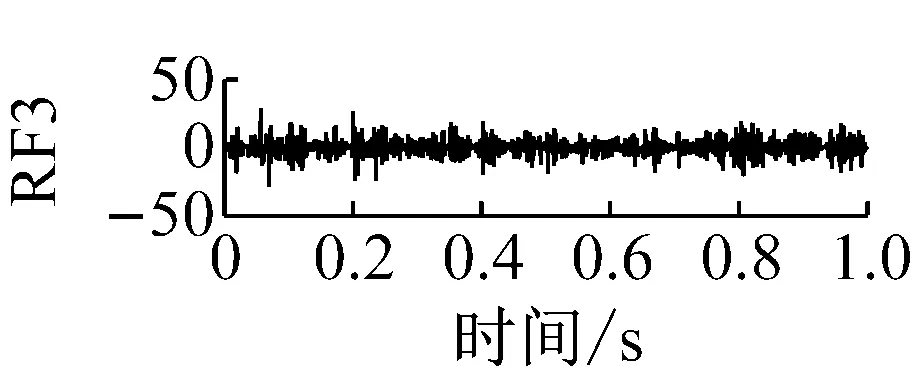
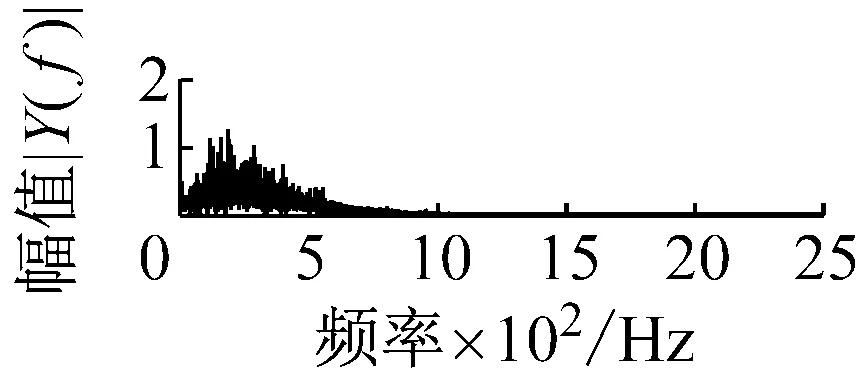
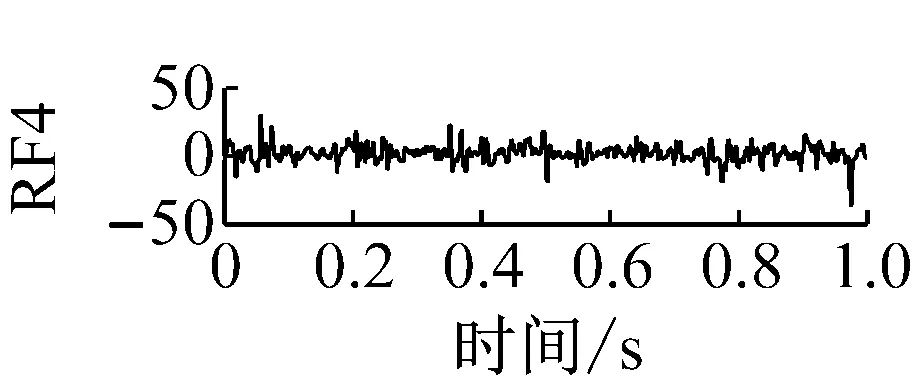
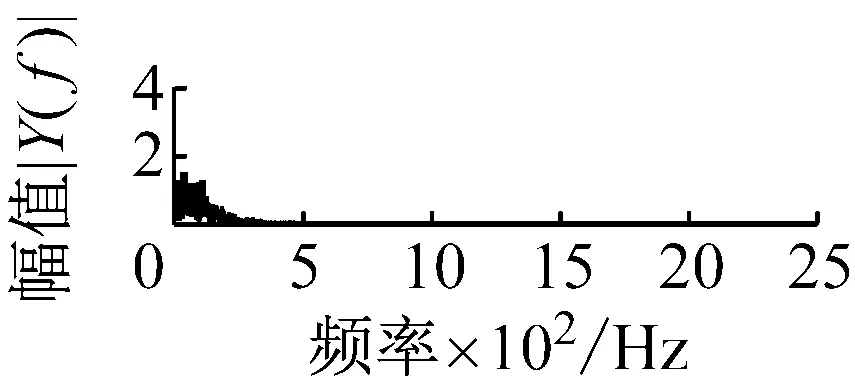
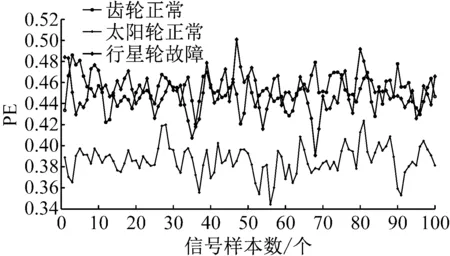
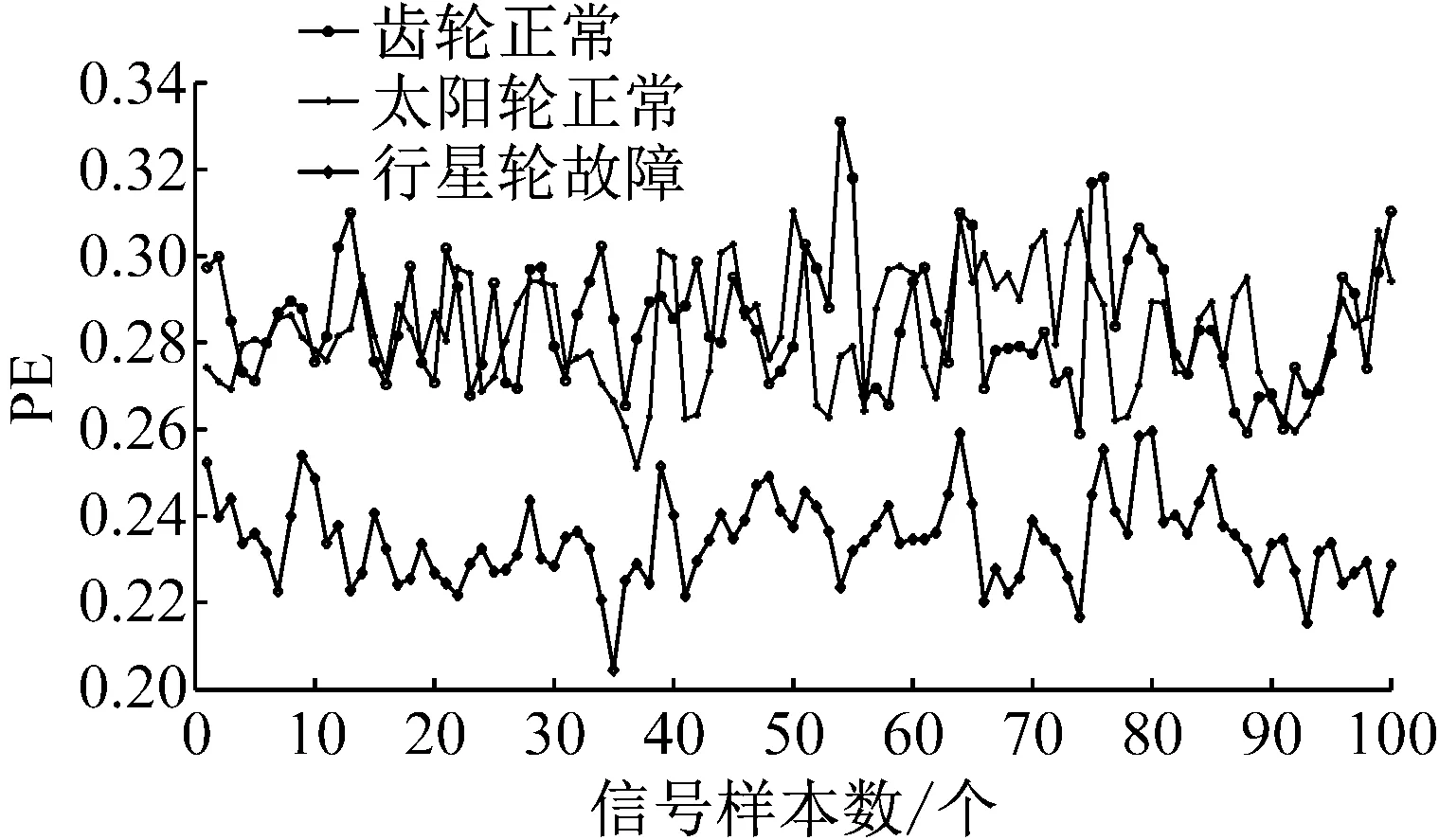
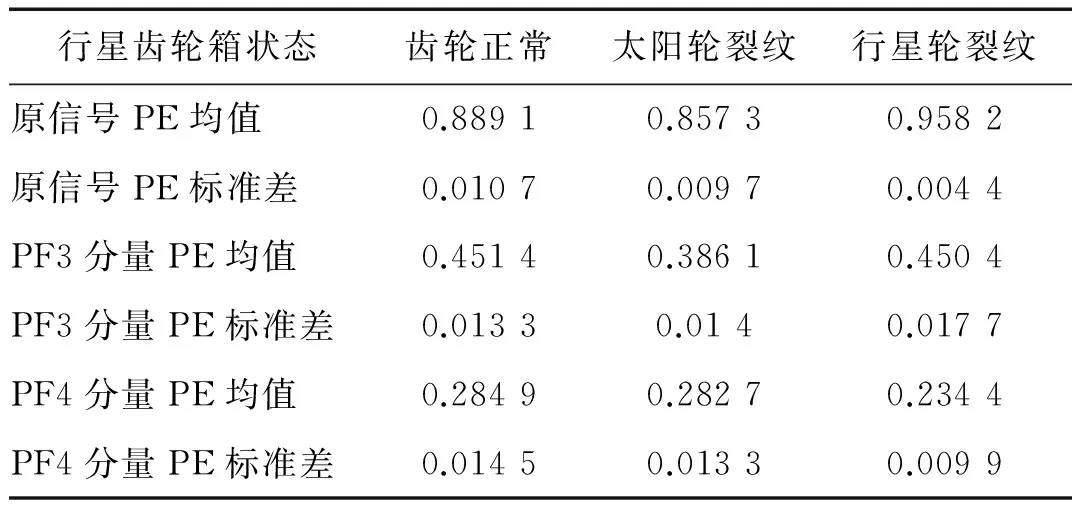
則根據ip和iq的大小排序，即當ip

x(j-(ip-1)τ)≤x(j-(iq-1)τ)

(5)

因此，對于重構矩陣Y的任一重構分量Y(j)都將得到一組位置索引序列

S(j)=(i1,i2,…,im)j=1,2,3,…,k

(6)

由于m維相空間映射不同的位置索引序列共有m!種，而各重構分量中升序排列序列可能存在相同，因此，k≤m!，其中S(j)為符號序列中的一種序列。

(3)計算熵值

計算每一種位置索引序列出現的概率p1,p2,…,pk，此時，時間序列X={x(i),i=1,2,3,…,n}的k種不同位置索引序列的排列熵(PE)可以根據信息熵的形式定義為

(7)

當pi=1/m!時，Hp(m)就達到最大值lnm!。

(4)歸一化

為了方便各運行狀態下的排列熵比較，通常用lnm!將Hp(m)進行歸一化處理，即

Hp=Hp(m)/lnm!

(8)

式中，0≤Hp≤1。

Hp值的大小反映時間序列X的不確定程度:Hp的值越小，說明時間序列越確定，反之，則時間序列不確定性越大。Hp的變化反映了時間序列的微小細節變化。

在計算過程中，延遲時間τ和嵌入維度m的選取對于排列熵的計算結果將產生一定的影響，對于延遲時間τ和嵌入維度m的選取，裝甲兵工程學院的馮輔周、司愛威和饒國強等人進行了深入的研究，使用以重構時間序列最佳相空間的方法確定模型參數，比較了不同確定方法對故障診斷結果的影響，最后得出參數模型獨立確定方法優于聯合確定方法，克服了排列熵參數人為主觀或憑經驗選擇的不確定性[12]。

3 試驗驗證

為了檢驗上述基于LMD和排列熵算法在行星齒輪箱振動信號分析中的應用效果，使用試驗驗證其實用性。在行星齒輪箱故障診斷中，齒輪裂紋是一種常見的故障，若不及時發現將擴展成斷齒，進而產生嚴重的后果，而齒輪裂紋故障信號微弱，對于齒輪裂紋的故障識別一直是一個難點，因此進行齒輪裂紋故障識別意義重大。本文分別對行星齒輪箱齒輪正常、太陽輪輪齒裂紋及行星輪輪齒裂紋三種狀態進行故障模擬試驗[13]，試驗臺示意圖如圖4所示，其中行星齒輪箱含有單一行星排，太陽輪為輸入，行星架為輸出。

圖4 行星齒輪箱試驗臺

試驗中，振動傳感器粘貼在行星齒輪箱的箱體上，齒輪箱輸入軸轉速即太陽輪轉速2 400 r/min，采集齒輪在正常、太陽輪裂紋及行星輪裂紋的行星齒輪箱振動信號數據，測試均在相同負載情況下完成，行星齒輪箱參數及各特征頻率如表1所示，太陽輪嚙合頻率、太陽輪故障特征頻率及行星輪故障頻率的詳細求解方法參照文獻[14]，表1中的故障特征頻率表示當太陽輪和行星輪出現裂紋故障時，實測信號在包含100 Hz和33.3 Hz的分量中存有故障信息。

采樣頻率設定為5 120 Hz，采樣時間為1 s，齒輪正常、太陽輪裂紋及行星輪裂紋故障的時域和頻域波形如圖5所示。由此三種狀態的頻域波形可得，邊頻帶集中在嚙合頻率和其倍頻附近，故障信息并不明顯，因此僅根據此時頻域分析并不能判斷行星齒輪箱是否存在故障。

表1 行星齒輪箱齒輪參數及頻率

(a) 齒輪正常

(b) 太陽輪裂紋故障

(c) 行星輪裂紋故障

Fig.5 Time and frequency domain waveforms of normal and fault planetary gearboxes

文獻[15]驗證了基于EMD和排列熵在旋轉機械中損傷檢測具有較好的結果，圖6為結合EMD和排列熵在行星齒輪箱振動分析中的檢測結果，由圖6可知，齒輪正常、太陽輪裂紋和行星輪裂紋排列熵值曲線出現多處交叉，均值無顯著差異，因此無法判斷各齒輪的故障情況，分析出現這一情況的原因可能是因為EMD對非線性非平穩信號適用性導致。

圖6 三種狀態下振動信號的EMD高頻部分排列熵

Fig.6 PE of EMD high-frequency part of three conditions vibration signal

采用本文提出的方法，首先使用LMD方法對上述三種運行狀態的振動信號進行分解，通過LMD分解可以將振動信號分解為包含不同頻段的多個PF分量信號，而行星齒輪箱的故障信息有可能包含在某個PF分量中，然后通過排列熵算法對包含有故障信息的PF分量進行計算，從而檢測出故障。為了確定包含故障信息的PF分量，對每個PF分量進行FFT變換，求其包含的頻率成分。正常狀態、太陽輪裂紋及行星輪裂紋的振動信號的分解結果及各個PF分量的頻域波形分別如圖7、圖8和圖9所示。

圖7 齒輪正常狀態下的LMD結果及頻域波形

Fig.7 LMD result and frequency domain waveforms of vibration signal of normal gear

圖8 太陽輪輪齒裂紋故障時的LMD結果及頻域波形

Fig.8 LMD result and frequency domain waveforms of vibration signal of fault sun gear

由圖7、圖8和圖9可知，包含行星齒輪箱嚙合頻率fm=667 Hz的高頻振動信號及其倍頻信號主要分布在PF1和PF2分量中，而包含頻率100 Hz的振動信號主要分布在PF3分量中，包含頻率33.3 Hz的低頻振動信號主要分布在PF4分量中，當太陽輪或行星輪出現局部故障時，包含此兩個頻率點的主要分量中存在故障信息。因此，為了診斷太陽輪和行星輪是否發生局部故障，只需分別計算PF3和PF4分量的排列熵，根據排列熵的結果即可判斷行星齒輪箱中太陽輪和行星輪的運行狀態。

圖9 行星輪輪齒裂紋故障時的LMD結果及頻域波形

Fig.9 LMD result and frequency domain waveforms of vibration signal of fault planetary gear

在三種狀態實測振動信號中，每種狀態采集100個樣本，選取每個樣本的數據長度為L=1 024，使用LMD方法分別將此三種狀態的100個樣本自適應分解成多個PF分量，對各狀態的PF3分量和PF4分量求取排列熵，根據參數模型獨立確定方法確定嵌入維度m=5，延遲時間t=1，得出的排列熵值如圖10和圖11所示。

圖10 三種狀態下振動信號的PF3分量的排列熵

圖11 三種狀態下振動信號的PF4分量的排列熵

根據排列熵的概念，排列熵反映了一維時間序列的復雜度，此處反映齒輪振動信號的復雜度。在轉速、負載相同的情況下，齒輪振動信號的排列熵越大，振動規律越隨機；反之，排列熵越小，振動規律越確定。當齒輪出現故障時，信號將出現沖擊，此時振動規律更確定，排列熵更小，因此如果某信號的排列熵小于正常信號的排列熵，則說明此信號為含有故障的信號。由圖10可知，其中一種狀態的PF3分量排列熵明顯小于其他兩種狀態PF3分量的排列熵，說明了此PF3分量為含有故障的信號，而此分量的主要頻率成分在100 Hz左右，由于太陽輪的故障特征頻率為100 Hz，故判斷此種狀態太陽輪發生了故障，結果與實際吻合。由圖11可知，其中一個狀態的PF4分量排列熵明顯小于其他兩種狀態PF4分量的排列熵，說明了此PF分量為含有故障的信號，而此分量的主要頻率成分在33.3 Hz左右，由于行星輪的故障特征頻率為33.3 Hz，故判斷為行星輪出現了故障，結果與實際吻合。

為了更精準的比較這三種狀態排列熵的差別，進一步證明結合LMD和排列熵方法的有效性，本文計算了未分解的原始信號、分解后的PF3分量和PF4分量的排列熵值均值以及其標準差值，計算結果，如表2所示。

表2 排列熵均值及標準差

由表2可知：

(1) 未經過LMD分解的原始信號的排列熵，行星齒輪裂紋故障的排列熵最大，太陽輪裂紋故障的排列熵最小，此結果并不能區分正常齒輪信號和故障齒輪信號，故不能作為判斷行星齒輪箱的狀態的依據。

(2) 在經過LMD分解后，PF3分量的排列熵中，太陽輪裂紋故障的排列熵明顯小于齒輪正常和行星輪裂紋故障的振動信號排列熵，而在PF4分量中，行星輪裂紋故障的排列熵明顯小于齒輪正常和太陽輪裂紋故障的排列熵，以此可作為判斷行星齒輪箱運行狀態的依據。

分析出現上述情況的原因可概括為，由于原始信號頻率成分復雜，規律性較差，排列熵也沒有規律，故而不能直接使用原始信號的排列熵作為判斷行星齒輪箱的運行狀態的依據。而在圖10中，含有100 Hz的PF3分量中，齒輪正常和行星輪裂紋故障時，各齒輪嚙合產生的沖擊信號在PF3分量中沒有明顯的沖擊，信號的差別是隨機的，主要由齒面加工誤差產生的表面不平度、波動度和齒形誤差造成，故而能量分布的隨機性強，不確定程度大，排列熵值高。而在太陽輪齒輪某個輪齒出現裂紋時，此輪齒剛度降低，齒輪在此輪齒嚙合時將產生與其他輪齒嚙合不同的沖擊，且此嚙合信號產生的沖擊更具有確定性，沖擊的頻率為100 Hz，故在其含有此頻率的PF3分量的排列熵更小，從而可判斷太陽輪出現了故障。而在圖11中，含有33.3 Hz的PF4分量中行星齒輪由于存在裂紋故障出現同樣的狀況，以此可診斷行星輪出現了故障，也進一步說明了基于LMD和排列熵的有效性。

4 結 論

本文提出一種行星齒輪箱故障診斷的新方法-基于LMD和排列熵的故障診斷方法，并運用這一算法對行星齒輪箱的振動信號數據進行處理，并得出以下結論：

(1)LMD作為一種近年來發展起來的自適應分解方法，能夠有效的將非線性、非平穩信號自適應的分解為多個分頻段的信號。排列熵作為一種新的數據處理方法，對于振動信號非常敏感，信號狀態的微小變化都能夠引起排列熵值的變化，且具有概念簡單、計算簡捷等特點。

(2)使用本文提出的基于LMD和排列熵的方法分解不同狀態的振動信號，并對含有故障信息的PF分量求其排列熵可有效診斷行星齒輪箱的故障，判斷其運行狀態。

(3)由于基于LMD和排列熵的方法可將診斷結果定位到各頻段，故而可用于行星齒輪箱的齒輪故障的診斷和識別，至于對除裂紋以外的其他故障的診斷，將做進一步的研究。

[1] 馮輔周，安鋼，劉建敏．軍用車輛故障診斷學[M]. 北京：國防工業出版社，2007：477-484．

[2] 雷亞國, 何正嘉, 林京, 等. 行星齒輪箱故障診斷技術的研究進展[J]. 機械工程學報, 2011, 47(19): 59-67.

LEI Yaguo, HE Zhengjia, LIN Jing, et al. Research advances of fault diagnosis technique for planetary gearboxes[J]. Journal of Mechanical Engineering, 2011, 47(19): 59-67.

[3] 孟宗, 李姍姍, 王亞超. 基于LMD和局域時頻熵的旋轉機械故障診斷方法[J]. 計量學報, 2015, 36(1):77-81.

MENG Zong, LI Shanshan, WANG Yachao. Method of rotating machinery fault diagnosis based on LMD and Local Time-frequency entropy[J]. Acta Metrological Sinica, 2015, 36(1):77-81.

[4] 于德介, 張嵬, 程軍圣, 等. 基于EMD的時頻熵在齒輪故障診斷中的應用[J]. 振動與沖擊, 2015, 36(1):26-29.

YU Dejie, ZHANG Wei, CHENG Junsheng. Application of EMD and time-frequency entropy in gear fault diagnosis[J]. Journal of Vibration and Shock, 2015, 36(1):26-29.

[5] 楊斌, 程軍圣. 基于LMD和主分量分析的齒輪損傷識別方法[J]. 振動、測試診斷, 2013, 33(5): 809-813.

YANG Bin, CHENG Junsheng. Method of gear damage identification based on LMD and principal component analysis[J]. Journal of Vibration, Measurement and Diagnosis, 2013, 33(5): 809-813.

[6] 程軍圣, 楊宇, 于德介. 局部均值分解方法及其在齒輪故障診斷中的應用[J]. 振動工程學報, 2009, 22(1): 76-84.

CHENG Junsheng, YANG Yu, YU Dejie. LMD method and its application in gear fault diagnosis[J]. Journal of Vibration Engineering, 2009, 22(1): 76-84.

[7] BANDT C, POMPE B. Permutation entropy: A natural complexity measure for time series[J]. Phys. Rev. Lett., 2002, 88(174102): 1-4.

[8] CAO Y, TUNG W, GAO J B, et al. Detecting dynamical changes in time series using the permutation entropy[J]. Phys. Rev. E, 2004, 4(7): 1-7.

[9] 劉永斌,龍潛，馮志華，等.一種非平穩、非線性振動信號檢測方法的研究[J].振動與沖擊 2007，26(12)：131-134.

LIU Yongbin, LONG Qian, FENG Zhihua, et al. Detection method of nonlinear and non-stationary signals[J]. Journal of Vibration and Shock, 2007, 26(12): 131-134.

[10] 馮輔周,饒國強,司愛威,等. 排列熵算法研究及其在振動信號突變檢測中的應用[J].振動工程學報.2012，25(2)：221-224.

FENG Fuzhou, RAO Guoqiang, SI Aiwei. Research and application of the arithmetic of PE in testing the sudden change of vibration signal[J]. Journal of Vibration Engineering, 2012，25(2)：221-224.

[11] 馮輔周，司愛威，饒國強，等．基于小波相關排列熵的軸承早期故障診斷技術[J] 機械工程學報，2012，29(3)：73-79．

FENG Fuzhou, SI Aiwei, RAO Guoqiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Journal of Mechanical Engineering, 2012，29(3)：73-79．

[12] 饒國強, 馮輔周, 司愛威, 等.排列熵算法參數的優化確定方法[J].振動與沖擊，2014,33(1):188-193.

RAO Guoqiang, FENG Fuzhou, SI Aiwei, et al. Method for optimal determination of parameters in permutation entropy algorithm[J]. Journal of Vibration and Shock, 2014,33(1):188-193.

[13] LEI Yaguo, HAN Dong, LIN Jing, et al. Planetary gearboxes fault diagnosis using an adaptive stochastic resonance method[J].Mechanical Systems and Signal Processing, 2013, 38(1):113-124.

[14] 馮志鵬, 趙鐳鐳, 褚福磊. 行星齒輪箱齒輪局部故障振動頻譜特征[J]. 中國電機工程學報, 2013, 33(5): 119-127.

FENG Zhipeng, ZHAO Leilei, CHU Fulei. Vibration spectral characteristics of localized gear fault of planetary gearboxes[J]. Proceedings of the CSEE, 2013, 33(5): 119-127.

[15] 馮輔周, 饒國強, 張麗霞, 等. 基于EMD和排列熵的軸承異常檢測方法研究[J].軸承，2013(2):53-56.

FENG Fuzhou, RAO Guoqiang, ZHANG Lixia. Research on abnormality detection method for bearings based on EMD and permutation entropy[J]. Bearing, 2013(2):53-56.

Applicationoflocalmeandecompositionandpermutationentropyinfaultdiagnosisofplanetarygearboxes

DIND Chuang, ZHANG Bingzhi, FENG Fuzhou, JIANG Pengcheng

(Department of Mechanical Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

Nowadays planetary gearboxes are widely used in military and civilian equipment, so studying fault diagnosis of planetary gearboxes is very significant. Aiming at the nonlinearity and nonstationarity of planetary gearboxes’ vibrations, and the weakness of fault feature signals during their operation, a fault diagnosis method for planetary gearboxes was proposed based on the local mean decomposition (LMD) and the permutation entropy. The vibration signals under different conditions were adaptively decomposed into several product functions (PFs) with LMD. The corresponding permutation entropies of the PFs containing fault information were computed, they were used to identify fault types. Finally, three kinds of vibration signals for a planetary gearbox fault analog test platform were collected, they were the vibration signals in the gear normal state, those for the sun gear with a cracked tooth and those for the planet gear with a cracked tooth. These vibration signals were decomposed with LMD and the corresponding permutation entropies were computed, the effectiveness of the proposed method was verified.

planetary gearbox; local mean decomposition (LMD); permutation entropy; fault diagnosis

國家自然科學基金(51205407)

2016-04-01 修改稿收到日期：2016-06-26

丁闖 男，博士生，1989年5月生

馮輔周 男，博士，教授，1971年3月生

TH212；TH213

： A

10.13465/j.cnki.jvs.2017.17.009