基于改進灰色關聯度的彈藥航空適運性評價指標體系構建

頡正陽，安紅，陳思楊

?

基于改進灰色關聯度的彈藥航空適運性評價指標體系構建

頡正陽a，安紅b，陳思楊c

（空軍勤務學院 a.學員一大隊；b.基礎部；c.航空軍交運輸指揮系，江蘇 徐州 221000）

針對彈藥航空運輸適運性評價的問題，首先分析彈藥航空運輸的特點和航空適運性影響因素，建立初始評價指標體系；然后，采用改進灰色關聯度模型對彈藥航空適運性初始評價指標體系進行優化，經過灰色關聯分析，剔除與適運性評價目標關聯不強的指標，采用德爾菲法對指標優劣排序進行調整，并利用相關性分析法去掉相關性較強的指標。得到優化的彈藥航空適運性評價指標體系，兼顧了指標的主觀性和客觀性。最后，通過實例驗證了模型的有效性和實用性。

彈藥；航空適運性；評價指標體系；改進灰色關聯度

以往彈藥大多數通過公路、鐵路方式進行運輸，運輸時間比較長，不能滿足越來越多的部隊應急機動作戰要求。隨著大型運輸機的部隊列裝，我軍空中投送能力將會得到極大的提升，通過航空方式運送彈藥，既快捷、又高效，已經逐漸成為中長距離彈藥運輸的重要方式之一。目前我軍彈藥航空軍事運輸尚處在起步階段，彈藥的航空適運性不清楚，能否使用軍用運輸機運輸彈藥成為首先要解決的難題。因此，有必要建立彈藥航空適運性評價指標體系。

航空適運性[1]，又稱航空運輸性，是指裝備適應航空運輸的固有能力，包括適應航空基礎設施、航空載運工具和航空運輸環境等。我國在適運性研究方面尚處在起步探索階段，關于適運性評價指標體系的研究有限。吳剛等人[2]運用灰色關聯度法和層次分析法建立了運輸性評價模型。王傳義等[3]對鐵路運輸中軍事裝備運輸性的影響因素進行系統分析，建立了運輸性評價指標體系，并運用灰色關聯分析建立了運輸性評價的數學模型。王會云[4]構建了加權灰色關聯決策分析模型，對備選后方儲備中心進行選擇。綜合來看，大部分文獻是對評價對象進行評價，而構建指標體系的文獻相對較少。彈藥航空適運性指標既有定性指標又有定量指標，并且指標間沒有確定的數量關系，是一種灰色系統。

文中針對灰色關聯度法在建立指標體系時只注重數據而不結合實際的缺點，提出一種基于改進灰色關聯度的彈藥航空適運性評價指標體系構建方法，將定性與定量分析相結合，建立更加符合實際的指標體系，指導人們解決彈藥航空適運性分析的問題。

1 初始評價指標體系建立

1.1 彈藥航空運輸特點

彈藥采用航空運輸，可實現直達供應、快速支援，具有速度快、保密性強、受外界干擾小等特點，具有公路、鐵路等運輸方式不具有的便捷性。

彈藥是指裝有火炸藥及其他裝填物，能對目標起毀傷作用或實現其他用途的裝備，包括槍彈、炮彈、火箭彈、手榴彈、槍榴彈、地雷、航空彈藥和艦艇彈藥等。從定義中就能看出，不同于航空運輸的其他貨物，彈藥在航空運輸中具有意外起火、噴射、爆炸等潛在危險性，能夠威脅到機組生命安全、飛機安全，造成重大人員傷亡和財產損失。不單單在運輸途中，在彈藥裝卸飛機的過程中，若不注意也會造成危險，是需要特殊對待的一類空運裝備。

1.2 影響因素分析

1）內部影響因素：內部影響因素主要指彈藥自身的物理、化學性質和包裝。物理性質主要是指彈藥的質量、重心、尺寸等的影響，比如某些彈藥過于集重而超過機艙地板承重限制；化學性質主要指彈藥在化學變化中表現出來的性質，比如可燃、放熱、爆炸等；包裝對于彈藥的安全運輸具有重要的作用，包裝的材質、構造均能夠影響彈藥的安全，一個滿足要求的包裝能夠更好地保護彈藥，降低發生危險的概率，也就是提高了其航空適運性。

2）外部影響因素：外部影響因素主要包括載運工具、運輸環境和裝卸要求。載運工具因素主要指運輸機自身的布局尺寸要求、貨艙地板（集裝板）的載荷限制（包括軸負荷、接地比壓等）、貨艙地板的固定與系留要求（包括系留的位置、數量、強度以及限動過載要求）；運輸環境主要指彈藥在航空運輸過程中所遇到的機械、氣候環境影響，其中機械環境包括振動、沖擊、穩態加速度和靜負載等因素，氣候環境包括貨艙溫度（高溫、低溫和溫度變化）、濕度、低氣壓等，彈藥可能因其影響而造成失效、起火、爆炸等危險；裝卸要求主要指待裝貨物適應不同裝卸方式的要求，根據貨物的尺寸質量，裝卸方式主要有滾裝滾卸（裝備貨物自行裝卸）、吊裝吊卸（采用機上吊具）、升降裝卸（采用升降裝卸平臺）、牽引裝卸（以電動絞車或牽引車為動力）。

1.3 建立彈藥航空適運性初始評價指標體系

根據彈藥航空運輸特點和彈藥航空適運性影響因素，以及相關文獻、部隊實踐的總結和專家指導意見，遵循全面性、實用性、代表性、科學性和可靠性的原則，建立了彈藥航空適運性初始評價指標體系，如圖1所示。

圖1 彈藥航空適運性初始評價指標體系

2 初始評價指標體系優化

建立的初始評價指標體系較為全面，但存在某些指標所含信息相似、指標的重要性無法區分、某些指標不適用于彈藥的問題，需要對所建立的初始評價指標體系進行優化。

2.1 初始指標值的獲取和標準化

彈藥航空適運性初始評價指標體系中既有定性指標，又有定量指標。對于定性指標，比如“滾裝滾卸適應性”等，可采用德爾菲法[5-6]確定其指標值；對于定量指標，比如“穩態加速度”等，根據具體實際獲取指標值。

為消除不同指標的量綱不同的影響，需要對獲取的指標值進行標準化處理。對于正向指標來說，比如“尺寸適應性”，要求越大越好；對于負向指標來說，比如“接地比壓”，要求越小越好。正向指標和負向指標的標準化式分別為：

(2)

式中：x為第個評價對象第個評價指標的實測數值；，分別為個評價對象中指標實測數值的相對最優值。

2.2 改進灰色關聯度模型的建立

為彌補灰色關聯度模型在指標體系建立過程中只分析數據不考慮實際的缺點，采用基于德爾菲法和相關性分析法的改進灰色關聯度模型，進一步得到篩選完善的評價指標體系。

2.2.1 灰色關聯度模型的建立

對于一個系統來說，如果能夠看清其內部的信息，稱這個系統為“白色系統”；如果無法了解其內部的信息，則稱其為“黑色系統”[7]。“灰色系統”正是介于這兩個系統之間，也就是只了解這個系統中的一部分信息。

灰色關聯度表示系統中指標之間的關聯程度，注重挖掘系統內部的聯系。灰色關聯度模型的基本思想[8]就是根據標準指標序列和實際指標序列曲線幾何形狀的相似程度來判斷指標與評價目標的聯系是否緊密，以此為依據判斷指標的取舍。灰色關聯度模型的建立步驟[9-10]如下：

1）確定參考數列和比較數列。分別為：

式中：0()為第個評價指標的最優數值，x為第個評價對象第個評價指標的實測數值。

2）求指標關聯系數。首先求得各指標實測值0()與最優值x()的差值，得到差值矩陣：

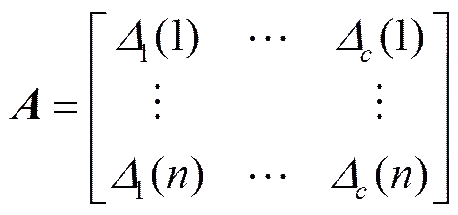
式中：Δ()表示第個評價對象第個指標與相應最優值的差值。

找出中的最大值和最小值分別記為max和min，由關聯系數式：

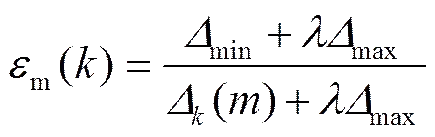
式中：為分辨系數，影響ε()的大小和分辨率，一般取值為0.5，可得到關聯系數矩陣：

3）求指標關聯度。根據關聯度的大小可得到指標的優劣順序，計算關聯度為：

最終可得到指標的關聯度矩陣：

2.2.2 德爾菲法調整指標排序

德爾菲法又稱專家調查法，通過對多名專家的問卷調查與反饋得到對某一問題的主觀認識[11]，是預測問題中一種有效的研究方法。德爾菲法調整指標排序的步驟如下[5-6]：

1）選取專家。選取名專家，專家應在本研究領域內具有一定學術水平，能夠準確反映指標的重要程度。

2）專家對評價指標進行評分。按照0～100的分值區間進行評分，評分過程要客觀公正，必要時可對指標評分加以說明。最后將結果進行標準化處理，得到專家評分矩陣：

3）計算名專家對每個指標的評分均值：

(5)

4）結合關聯度r，計算τ：

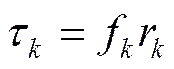
將計算結果進行排序，得到指標排序矩陣=[(1)，…，()]。

2.2.3 相關性分析剔除重復指標

經過德菲爾法的分析后，指標體系得到了調整，但是經過灰色關聯度分析和德爾菲法調整后得到的指標排序只是各指標與評價目標之間的關聯性的排序，沒有考慮指標之間的相關性，導致兩個相關性大的指標都保留，造成包含信息重復的問題。

相關性分析[12]是對兩個變量之間的關系程度進行分析，它以相關系數作為這兩個變量之間相關強弱程度的度量。相關系數有三種，分別為Pearson積距相關系數（指標是定距數據、正態分布和線性關系）、Spearman秩相關系數和Kendall相關系數（分類指標為有序變量）。文中指標數值的分布未知，且為無序指標，故采用Spearman秩相關系數確定指標之間的相關性。兩個指標之間的相關系數為：

式中：r是第個評價對象關于指標的秩；s是第個評價對象關于指標的秩；為評價對象的個數，，分別為r，s的平均值。

相關系數的取值范圍[13]為[－1,1]，=0表示指標間不存在相關關系；||>0.8表示指標間存在較強的相關關系；||<0.3表示指標間相關關系較弱。

3 實例分析

為構建完善的彈藥航空適運性評價指標體系，現選取四種不同種類彈藥（分別用A，B，C，D來代表）的各項指標數據，采用改進的灰色關聯度模型對初始評價指標體系進行篩選優化。

3.1 指標值的獲取

根據四種彈藥航空適運性評價各指標相關數據以及專家的打分情況，得到各指標的原始值，再由式（1），（2）進行指標標準化，得到四種彈藥各指標的標準化數值，見表1。

表1 彈藥航空適運性評價指標標準化值

3.2 指標灰色關聯度分析

確定四種彈藥各指標的參考數列：0={1,1,…,1}；以及比較數列：1，2，3，4，數列中的指標值由表1給出。然后計算參考數列和比較數列相對應指標的差值，得到差值矩陣：

中最大值為0.997，最小值為0.026，由式（3）得到關聯系數矩陣：

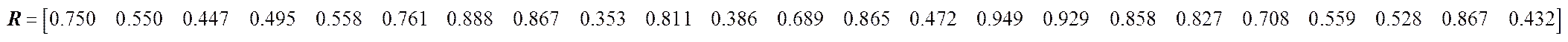
可得指標的相關度由大到小排序為：15，16，7，8，22，13，17，18，10，6，1，19，12，20，5，2，21，4，14，3，23，11，9。根據各指標關聯度的大小，可以將以下與適運性評價目標關聯度比較小的指標剔除：9，11，23。

3.3 指標的篩選優化

選取彈藥航空運輸領域內的5名專家對剩余指標進行評分，得到專家評分矩陣：

按照式（5）,（6）進行計算，得到最終專家評分矩陣′：

將評分結果排序，再和灰色關聯度排序結果進行對比，得到優化的評價指標排序結果為：20，19，21，7，8，22，2，3，15，16，17，18，10，6，1，12，5，4，14。利用Spss數據分析軟件[14]對20個指標進行相關性分析，采用雙側檢驗得到各指標之間的相關性系數。以“物理適應性”和“振動適應性”為例進行介紹，得到兩個指標的Spearman秩相關系數，見表2。雖然兩個指標之間的相關性系數為0.800，但是顯著性水平為0.200，大于0.05，可知指標“物理適應性”和“振動適應性”之間顯著不相關。依次可得到各指標之間的相關性系數，相關性分析結果顯示，“物理適應性”和“尺寸適應性”、“重心”、“質量”、“接地比壓”之間顯著相關，故將“物理適應性”指標剔除。

表2 指標相關性分析結果

3.4 最終評價指標體系的確定

根據灰色關聯度分析、德爾菲法和指標相關性分析的優化，最終得到彈藥航空適運性評價指標體系，如圖2所示。

圖2 彈藥航空適運性最終評價指標體系

4 結語

通過改進灰色關聯度模型對初始評價指標體系進行優化，最終構建的彈藥航空適運性評價指標體系兼顧了客觀性、主觀性與實用性，而且指標的重要程度排序一目了然，為部隊進行彈藥航空適運性評價提供了較為可信的指標體系。但也存在以下問題，實例分析中選取的指標數據較少，導致指標的相關性分析精確度偏低，這是下一步需要改進的地方。

[1] MIL-STD-1366D, Interface standard for Transportability criteria[S].

[2] 吳剛, 劉將. 基于灰色關聯度法的運輸性評價模型[J]. 裝備指揮技術學院學報 2008, 19(4): 38-42.

[3] 王傳義, 高立軍, 段志浩. 鐵路運輸中軍事裝備運輸性評價研究[J]. 國防交通工程與技術, 2013(5): 38-43.

[4] 王會云. 基于熵權灰色關聯分析的儲備中心庫選擇[J]. 后勤工程學院學報, 2016, 32(1): 64-68.

[5] 劉偉濤, 顧鴻, 李春洪. 基于德爾菲法的專家評估法在海戰效能評估中的應用[J]. 海軍學術研究, 2011(5): 31-33.

[6] SCHMIDT R, LYYTINEN K, KEIL M, et al. Identifying Software Project Risks: An International Delphi Study[J]. Journal of Management Information Systems, 2001,17(4): 5-36.

[7] 鄧聚龍. 灰色系統理論與教程[M]. 武漢: 華中理工大學出版社, 1990: 21-30.

[8] 劉思峰, 黨耀國, 方志耕. 灰色系統理論及其應用(第三版)[M]. 北京: 科學出版社, 2004: 15-22.

[9] 雷蕾, 譚躍進. 招標方法的適用性研究[J]. 空軍工程大學學報(自然科學版), 2003, 4(3): 87-91.

[10] 王琦. 我國國有石油公司天然氣業務國際競爭力研究—基于AHP-灰色關聯度模型[J]. 甘肅科學學報, 2015, 27(2): 134-137.

[11] 秦麟征. 預測科學——未來研究學[M]. 北京: 方志出版社, 2007: 142-167.

[12] JOHN A R. Mathematical Statistics and Data Analysis [M]. Duxbury Press,1994 :421-427.

[13] 馮杰, 羅云, 曾珠, 等. 特種設備安全績效與安全監管能力相關性研究[J]. 中國安全科學學報, 2012, 22(2): 170-175.

[14] 李洪成. SPSS18數據分析基礎與實踐[M]. 北京: 電子工業出版社, 2011: 35-53.

Construction of Evaluation Index System about Ammunition Air Transportation Fitness Based on Improved Grey Relational Degree

JIE Zheng-yanga, AN Hongb, CHEN Si-yangc

(Air Force Logistics College a.Cadet Brigade 1; b.Department of Basic; c.Department of Airway Military Transportation Command System, Xuzhou 221000, China)

The paper aims to evaluation the ammunition air transportation fitness. Firstly, the ammunition air transportation characteristics and the influencing factors of air transportation fitness were analyzed, and an initial evaluation index system was built. Secondly, the evaluation index system for ammunition air transportation fitness was optimized based on the model of the improved grey relational degree. After the grey correlation analysis, the indexes without strong correlation with the evaluation goal were removed. The order of indexes was adjusted with Delphi method, and the indexes with strong correlation were removed by correlation analysis. An optimized evaluation index system about ammunition air transportation fitness was got. It gave consideration to the subjectivity and objectivity of indexes. Finally, the validity and practicality of the model were tested and verified in a case study.

ammunition; air transportation fitness; evaluation index system; improved grey relational degree

10.7643/ issn.1672-9242.2017.09.004

TJ01；E234

A

1672-9242(2017)09-0016-06

2017-05-11；

2017-06-08

頡正陽（1993—），男，碩士研究生，主要研究方向為運輸機運用工程。