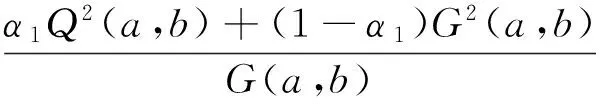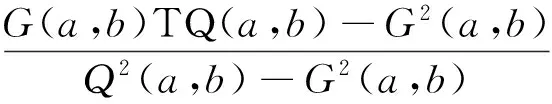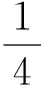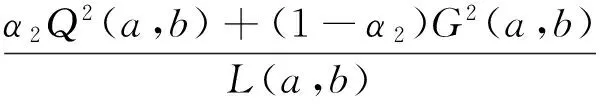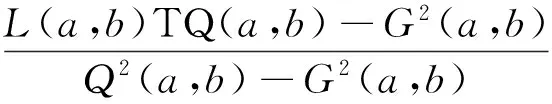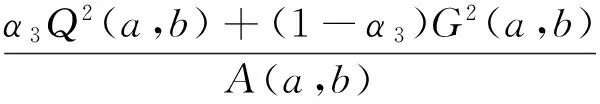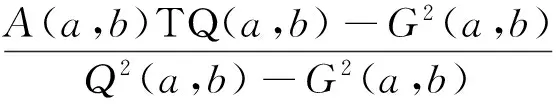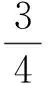Toader-Qi平均與其他二元平均的幾個確界
徐會作, 錢偉茂
(1.溫州廣播電視大學 經管學院, 浙江 溫州 325000; 2.湖州廣播電視大學 遠程教育學院, 浙江 湖州 313000)
Toader-Qi平均與其他二元平均的幾個確界
徐會作1, 錢偉茂2
(1.溫州廣播電視大學 經管學院, 浙江 溫州 325000; 2.湖州廣播電視大學 遠程教育學院, 浙江 湖州 313000)
研究了Toader-Qi平均TQ(a,b)關于幾何平均G(a,b)、對數平均L(a,b)、算術平均A(a,b)和二次平均Q(a,b)若干特殊組合的序關系.運用實分析方法以及第1類Bessel函數的乘積公式,建立若干重要引理,導出了4個關于Toader-Qi平均TQ(a,b)的精確不等式,并獲得了特殊情形的結果.
Toader-Qi平均;幾何平均;對數平均;算術平均;二次平均.
0 引 言
設a,b>0和a≠b,則幾何平均G(a,b)、指數平均I(a,b)、對數平均L(a,b)、算術平均A(a,b)、 二次平均Q(a,b)和Toader-Qi平均TQ(a,b)[1-3]分別為
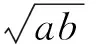
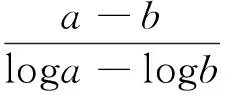
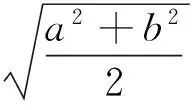
(1)
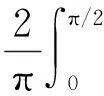
(2)
近年來,關于若干經典平均與Toader-Qi平均的比較受到了關注,得到了一定的研究,有關Toader-Qi平均的重要不等式可參閱文獻[2-7].QI等[2]證明了
(3)
和不等式
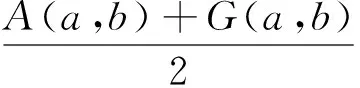
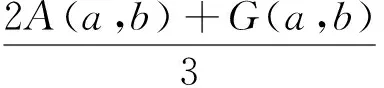
對所有a,b>0和a≠b成立, 并且
(4)
是第1類改進Bessel函數[8].
YANG等[4]證明了
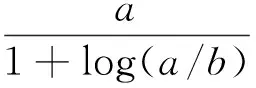
對所有a>b>0成立, 并且
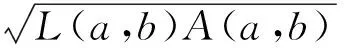
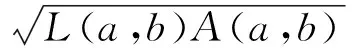
Lα2(a,b)A1-α2(a,b) β2L(a,b)+(1-β2)A(a,b) 由文獻[6],推得精確不等式 TQ(a,b)>L3/2(a,b) 設a>b>0,t=(loga-logb)/2>0,則由式(1)可推得 (5) 由式(2)和(3)可推得 (6) 本文的主要目的是給出以下幾個關于Toader-Qi平均與幾何平均G(a,b)、對數平均L(a,b)、算術平均A(a,b)和二次平均Q(a,b)特殊組合的精確不等式: 對所有a,b>0和a≠b成立. 為了證明主要結果, 本節給出一些經典Gamma函數、第1類Bessel函數的基本知識和相關引理. Γ(n+1)=nΓ(n)=n!, 對所有正整數n成立. 設v>-1,第1類修正Bessel函數Iv(t)定義(見文獻[10],p77)為 (7) 注意到在特殊情形下有: (8) (9) 引理2(見文獻[3],引理2.8) 設I0(t)定義為式(4).則等式 對所有t∈R成立. 引理3等式 (A) 與 (B) 對所有t∈R成立. 證明(A)由式(8)和Cauchy乘積公式(見文獻[12],(3.5)) 對所有t∈R,有 (B) 由式(9)和Cauchy乘積公式(見文獻[12], (3.5)) 對所有t∈R,有 證明由式(4)得 (10) 其中, (11) 經簡單計算得到 (12) 證明由引理3(B)得到 (13) 其中, (14) (15) (16) 其中, (17) (18) 證明由引理2得到 (19) 其中, (20) 經簡單計算得到 (21) 定理1雙向不等式 (22) 對所有a,b>0和a≠b成立當且僅當α1≤0且β1≥1/8. 證明不等式(22)可寫成如下形式: (23) 因G(a,b),Q(a,b)和TQ(a,b)是對稱和一階齊次的, 不失一般性, 假設a>b>0,t=(loga-logb)/2>0, 則由式(5)和(6),不等式(23)變成 α1 (24) 其中函數f(t)的定義見引理4. 注意到 (25) 由不等式(23)(24)和等式(25)協同引理4,則不等式(22)對所有a,b>0和a≠b成立當且僅當α1≤0且β1≥1/8. 定理2雙向不等式 (26) 對所有a,b>0和a≠b成立當且僅當α2≤0且β2≥5/24. 證明不等式(26)可改寫成 (27) 因G(a,b),L(a,b),Q(a,b)和TQ(a,b)是對稱和一階齊次的, 不失一般性, 假設a>b>0,t=(loga-logb)/2>0, 則由式(5)和(6),不等式(27)變成 α2 (28) 其中函數g(t)的定義見引理5. 注意到 (29) 由不等式(27)(28)和等式(29)協同引理5,則不等式(26)對所有a,b>0和a≠b成立當且僅當α2≤0且β2≥5/24. 推論2雙向不等式 對所有t∈(0,+∞)成立. 定理3雙向不等式 (30) 對所有a,b>0和a≠b成立當且僅當α3≤0且β3≥3/8. 證明不等式(30)可改寫為 (31) 因G(a,b),A(a,b),Q(a,b)和TQ(a,b)是對稱和一階齊次的,不失一般性, 假設a>b>0,t=(loga-logb)/2>0, 則由式(5)和(6),不等式(31)變成 α3 (32) 其中函數h(t)的定義見引理6. 注意到 (33) 由不等式(31)(32)和等式(33)協同引理6,則不等式(30)對所有a,b>0和a≠b成立當且僅當α3≤0且β3≥3/8. 推論3雙向不等式 對所有t∈(0,+∞)成立. 定理4雙向不等式 (34) 對所有a,b>0和a≠b成立當且僅當α4≤0且β4≥1/4. 證明不等式(30)可改寫為 (35) 不失一般性, 假設a>b>0,t=(loga-logb)/2>0, 則由式(5)和(6),不等式(34)變成 α4 (36) 其中函數k(t)的定義見引理7. 注意到 (37) 由不等式(35)(36)和式(37)協同引理7,則不等式(34)對所有a,b>0和a≠b成立當且僅當α4≤0且β4≥1/4. [1]TOADERG.Somemeanvaluesrelatedtothearithmetic-geometricmean[J].JournalofMathematicalAnalysisandApplications,1998,218(2):358-368. [2] QI F, SHI X T, LIU F F, et al. A double inequality for an integral mean in terms of the exponential and logarithmic means[J].PeriodicaMathematicaHungarica,2016.Doi:10.1007/s10998-016-0181-9. [3] YANG Z H. Some sharp inequalities for the Toader-Qi mean[J]. arXiv:1507.05430. [4] YANG Z H, CHU Y M. On approximating the modified Bessel function of the first kind and Toader-Qi mean[J].JournalofInequalitiesandApplications,2016,2016(1):40. [5] YANG Z H, CHU Y M, SONG Y Q. Sharp bounds for Toader-Qi mean in terms of logarithmic and identic means[J].MathInequalAppl,2016,19(2):721-730. [6] YANG Z H, CHU Y M. A sharp lower bound for Toader-Qi mean with applications[J].JournalofFunctionSpaces, 2016: Article ID 4165601. file:///D:/Users/Administrator/Downloads/4165601.pdf. [7] GUO B N, QI F. Some inequalities and absolute monotonicity for modified Bessel functions of the first kind[J].CommunKoreanMathSoc,2016,31(2):355-363. [8] ABRAMOWITZ M, STEGUN I A.HandbookofMathematicalFunctions:WithFormulas,Graphs,andMathematicalTables[M]. New York: Dover Publications,1965. [9] ANDERSON G D, VAMANAMURTHY M K, VUORINEN M. Conformal Invariants, Quasiconformal Maps, and Special Functions[C]//QuasiconformalSpaceMappings. Heidelberg: Springer,1992:1-19. [10] WATSON G N.ATreatiseontheTheoryofBesselFunctions[M]. Cambridge: Cambridge University Press,1995. [12] THIRUVENKATACHAR V R, NANJUNDIAH T S. Inequalities concerning Bessel functions and orthogonal polynomials[J].ProceedingsMathematicalSciences,1951,33(6):373-384. XU Huizuo1, QIAN Weimao2 (1. School of Economics and Management, Wenzhou Broadcast and TV University, Wenzhou 325000, Zhejiang Province, China; 2. School of Distance Education, Huzhou Broadcast and TV University, Huzhou 313000, Zhejiang Province, China) This paper study the order relation of some special combinations of geometric meanG(a,b), logarithmic meanL(a,b), arithmetic meanA(a,b) and quadratic meanQ(a,b) for Toader-Qi mean TQ(a,b). By using the method of real analysis in mathematics and the product formula of the first kind Bessel function, several important lemma are established, and four optimal inequalities for Toader-Qi mean TQ(a,b) are found. The results of particular cases are also presented. Toader-Qi mean;geometric mean;logarithmic mean;arithmetic mean;quadratic mean O 174.6 :A :1008-9497(2017)05-526-05 2016-11-02. 浙江廣播電視大學科研課題(XKT-15G17). 徐會作(1978-),http://orcid.org/0000-0002-9989-2672,男,講師,碩士,主要從事平均值不等式研究,E-mail:21888878@qq.com. 10.3785/j.issn.1008-9497.2017.05.005 SomesharpboundsforToader-Qimeanofotherbivariatemeans. Journal of Zhejiang University(Science Edition), 2017,44(5):526-530


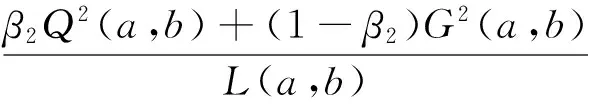
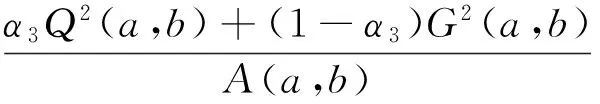
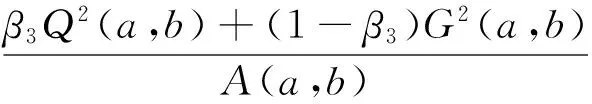
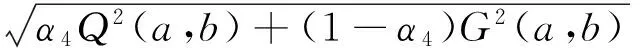
1 預備知識和引理

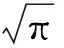
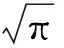
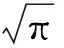


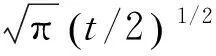

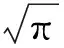
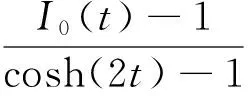
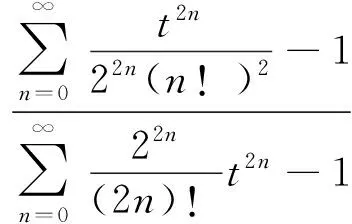
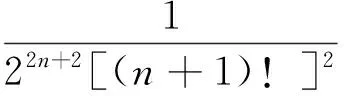
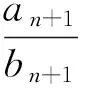
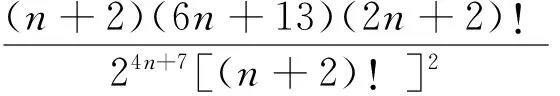
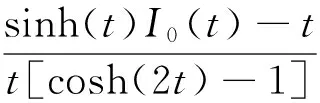
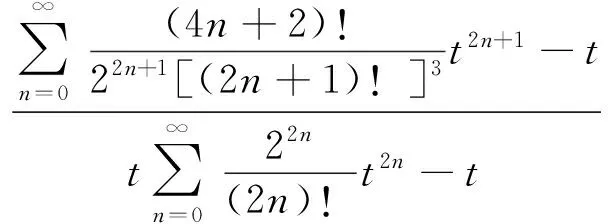
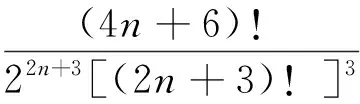
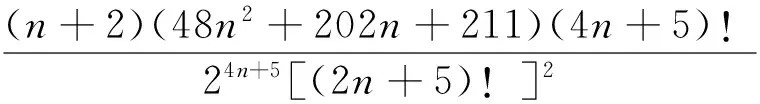
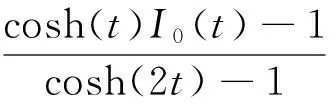
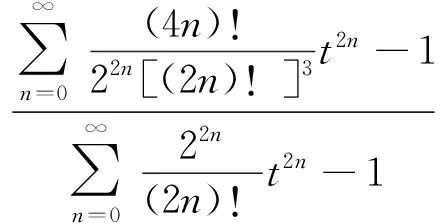
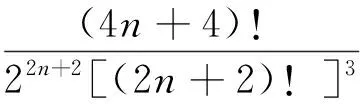
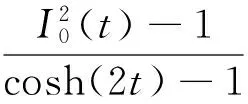

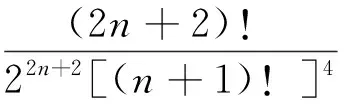
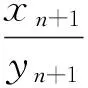
2 主要結果及證明