OGS軟件在地質災害監測預警系統中的應用

丁靖洋

（北京市地質工程勘察院，北京 100048）

OGS軟件在地質災害監測預警系統中的應用

丁靖洋

（北京市地質工程勘察院，北京 100048）

地質災害對交通網絡線性工程的安全性構成重大威脅。本文依托于“京張鐵路（居庸關隧道進口段）地質安全監測示范工程”項目，以一處堆渣體為研究對象，基于有效應力原理、Mohr-Coulomb屈服準則、Richard-flow非飽和滲流方程，采用OGS軟件對降雨入滲條件下的流固耦合過程進行數值模擬。研究結果表明，隨著降雨強度的不斷增加，堆渣體上部土體的有效飽和度逐漸增大，地災發生區域開始出現并相互貫通，這將為地質安全預警提供依據。

地質災害預警；降雨入滲；流固耦合；OGS數值模擬

0 前言

北京地區以中低山地貌為主，其中山區面積約占全市面積的62%，且溝谷分布廣泛，地形相對高差較大，巖體較為破碎，地質構造復雜，新構造活動強烈；北京降水多集中在7—8月，且時常有暴雨、大暴雨發生；加之隨著經濟社會的發展，人類活動對地質體環境的影響日趨明顯。因此北京山區內的地質災害，尤其泥石流、滑坡、崩塌、采空塌陷等較為嚴重。據統計，北京地區包含泥石流591條、滑坡15個、崩滑塌34550個、采空塌陷162個（董桂芝等，1997）。

作為“京津冀一體化”交通網絡建設的重要組成部分，京張城際鐵路的地質安全性尤其引人注意。由于交通網絡線性工程的特點，地質災害的發生將對其造成巨大損失。其中京張城際鐵路（北京段）穿越軍都山，沿途存在多種不良地質災害，為了確保京張城際鐵路在建設、運行中的安全，對沿線周邊不良地質災害體進行實時監測并及時預警具有重要意義。

京張鐵路（居庸關隧道進口段）地質安全監測示范工程，是京津冀協同發展交通網絡地質安全監測預警系統建設中的試驗研究項目。本文在該示范工程試驗區選址的基礎上，以一處堆渣體為分析對象，通過對三維地質數據的處理建立了有限元計算模型，基于有效應力原理、非飽和滲透原理和Mohr-Coulomb塑性理論，對堆渣體位移與降雨量關系、滲流-應力耦合過程和潛在危險區域進行了研究。

1 工程背景

試驗區位于北京市昌平區姚店一處采石場，面積約0.5km2，地面高程約285m，山體自然坡度一般為25°～59°，區內整體地形呈兩側高，中間低，地形起伏，橫向“V”型沖溝發育，均匯入中部低洼處的縱向河谷中，局部成陡崖巖墻狀。

通過野外調查發現，試驗區內發育有一條泥石流溝，溝谷長度較長，規模較大，為V型溝。溝內主要物源為采石場開采過程中產生的廢石、廢渣和大量松散坡積物，稱之為“堆渣體”。

為了便于地質災害的現場監測預警，試驗區內布設有GNSS、靜力水準、SAA、測斜儀、土壓力計、地下水動態自動監測儀等設備，24小時自動記錄數據，監測內容包括降雨量、水平/垂直位移、土壓力、土壤含水率和地下水滲透率等。

2 三維建模工作

2.1 三維地質體展示模型

借助于Creater建模軟件平臺，在對堆渣體鉆孔數據進行篩選及處理的基礎上，開展三維地質體展示模型的構建工作。堆渣體建模分為3個地層、10個剖面，其中從上到下地層分別為坡積物層、坡積碎石及碎石層和基巖層。

2.2 三維地質體模型網格剖分

建模分析工作以OpenGeoSys (OGS) 數值計算軟件為平臺：OpenGeoSys是針對孔隙介質中熱-水-力-化學（THMC）多場耦合過程的國際著名開放性數值模擬平臺，其提供地質和水力方面的多場耦合有限元計算框架平臺，軟件程序允許C++語言進行嵌入編程。

基于三維展示模型獲得的堆渣體高程數據，導出了數據散點形式的不規則三角形文件(TINs)格式。通過自行編寫的C++語言程序，讀取TINs格式文件數據，從而建立了GMSH網格文件（.Geo）。為了減少數值計算工作量，模型減少了底層基巖的厚度。

通過GMSH軟件自動劃分了四面體網格，基于Frontal算法，有限單元網格劃分如圖1所示，數值計算單元共24498個。

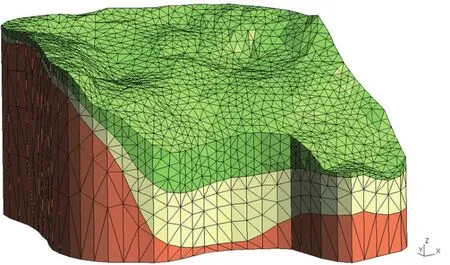
圖1 數值模擬有限單元網格模型Fig.1 Finite Element Mesh of the model

3 非飽和滲流-應力耦合理論

3.1 有效應力原理

降雨誘發地質災害的過程本質上為非飽和孔隙介質入滲的過程，即滲流—應力耦合過程。在描述非飽和孔隙介質入滲過程的應力分量理論中，最為廣泛應用的理論為有效應力原理（Terzaghi，1923）。

在降雨誘發地質災害的過程中，堆渣體中的孔隙壓力隨降雨入滲而不斷變化。Bolzon 等（1996）通過熱力學理論對非飽和土中的能量方程進行了驗證，從而得到了非飽和有效應力公式為：

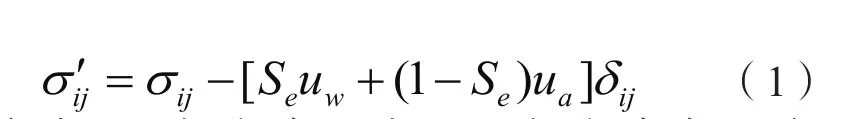
式中：S為孔隙吸力，uw為孔隙水壓力，uα為孔隙氣壓力，Se為有效飽和度，δij為克羅內克（Kroenker delta）符號。

本次研究工作中，堆渣體坡積物以碎石土為主，孔隙率較大，故忽略孔隙氣壓力uα，只考慮孔隙水壓力uw對滲流-應力耦合過程的影響。因此，有效應力公式為

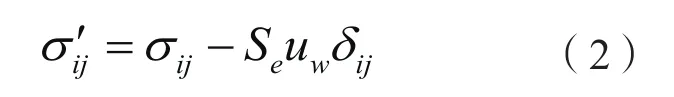
需要說明的是，Bolzon推導的有效應力公式引入了有效飽和度Se這一參數，表征了降雨入滲對非飽和孔隙介質的影響。當飽和度為1時，Bolzon有效應力公式可退化為太沙基公式。

孔隙介質中的應力應變理論基于Hook定律。在OpenGeoSys中，采用返回映射算法計算彈塑性應力應變增量。

3.2 考慮入滲影響的Mohr-Coulomb理論

Mohr-coulomb屈服準則廣泛應用于描述巖土體的塑性力學行為，其表達式為

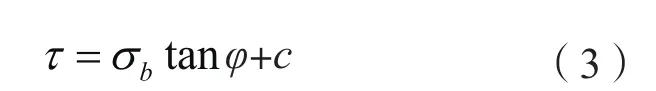
式中：τ為剪切應力，σb為主應力，φ和c分別為內摩擦角和粘聚力。

若考慮降雨入滲對巖土體屈服準則的影響，則引入有效應力作為Mohr-Coulomb準則的主應力，將式（2）代入式（3），可得

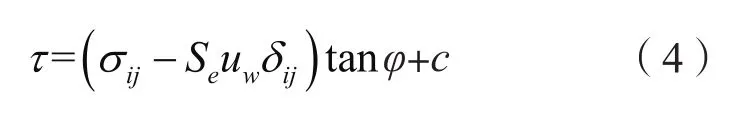
3.3 非飽和滲流理論

若忽略物質溶解，則孔隙介質中的流體流動應遵循質量守恒定律。以達西尺度的代表性體積單元（RVE）為例，RVE內流體質量的變化量與通過RVE邊界的流體質量應相等。對不可變形孔隙介質，在無源、無匯的情況下，流體質量守恒關系表達式為

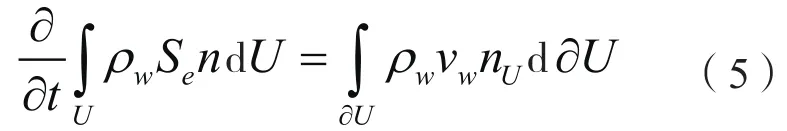
式中：下標w代表孔隙介質中的某流體相，ρw為孔隙介質中流體的密度，Se表示孔隙介質中流體相的有效飽和度，n為孔隙介質孔隙度，vw為流體流過RVE的流速，nu為在RVE邊界上沿流動方向的單位向量，?U為RVE的邊界。

Richard方程（Richards，1931）是描述非飽和孔隙介質流動的經典方程。對式（5）進行積分，由鏈式微分法則，引入達西方程，考慮孔隙介質形變對流體質量平衡的影響，則Richard滲流本構方程為：

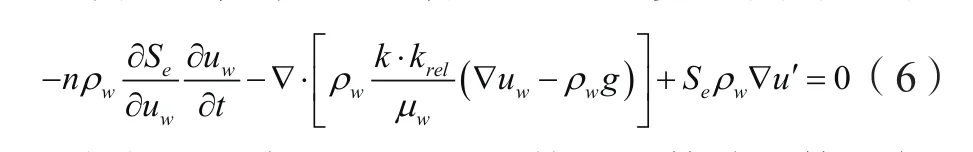
式中：孔隙吸力 用毛細管壓力等效，等于負孔隙水壓力，即uw=-S，k為孔隙介質固有滲透率，krel為非飽和到飽和過程中的相對滲透率，μw為流體粘性系數。毛細管壓力與有效飽和度的關系（通常稱為土水特征曲線，Water Retention Curve, WRC）將通過Van Genuchten模型確定（Genuchten，1980），即

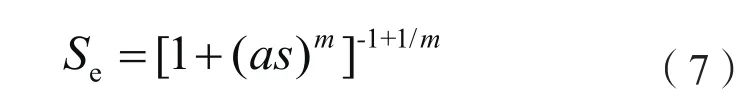
式中：a和m為相關力學參數。

相對滲透率公式采用冪函數形式如：

4 數值模擬參數

4.1 力學參數

堆渣體自上而下分別為坡積物層、坡積碎石及碎石層和基巖層，根據現場勘察資料、室內土工試驗及參考《工程地質手冊》，并借助于國內外學者的相關研究成果（王新剛等，2013；胡凱衡等，2014；黃龍波等，2016；陳善雄等，2001；徐晗等，2005），確定數值模擬所需的力學參數（表1）。

4.2 滲流參數

對于滲流參數，堆渣體非飽和到飽和過程中的相對滲透率采用公式（8）計算。數值模擬中的滲流參數見表2。

本次研究工作中的土水特征曲線（WRC）引用了文獻（Cho，2016）中的數據，通過提取數據，得到了土水特征曲線如圖2(a)，相對滲透率計算結果如圖2(b)所示。

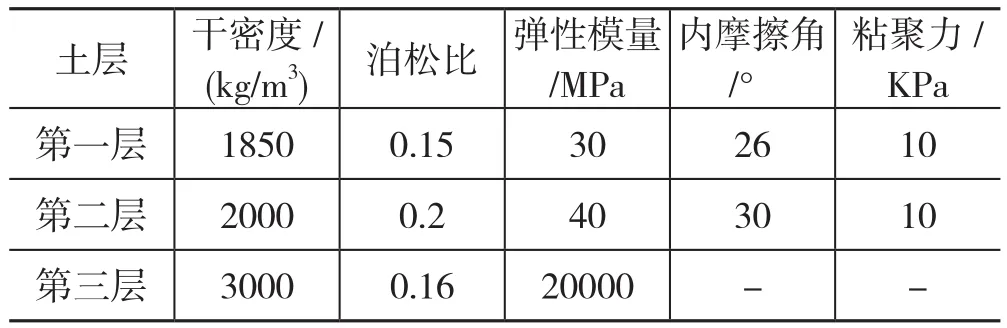
表1 數值模擬力學參數Tab.1 Mechanics parameters for the numerical modeling

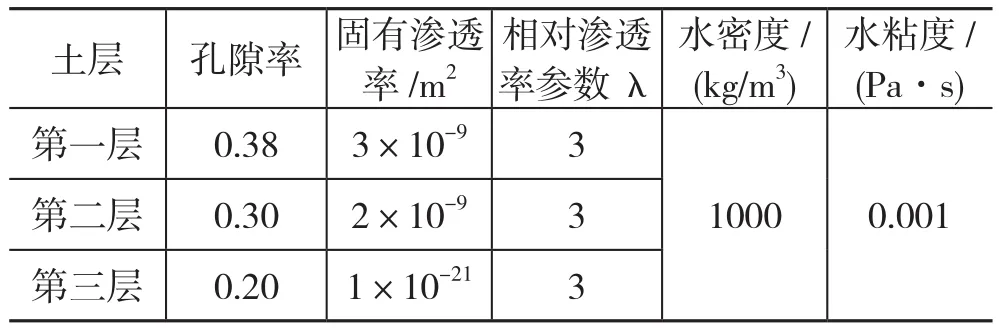
表2 數值模擬滲流參數Tab.2 Seepage parameters for the numerical modeling

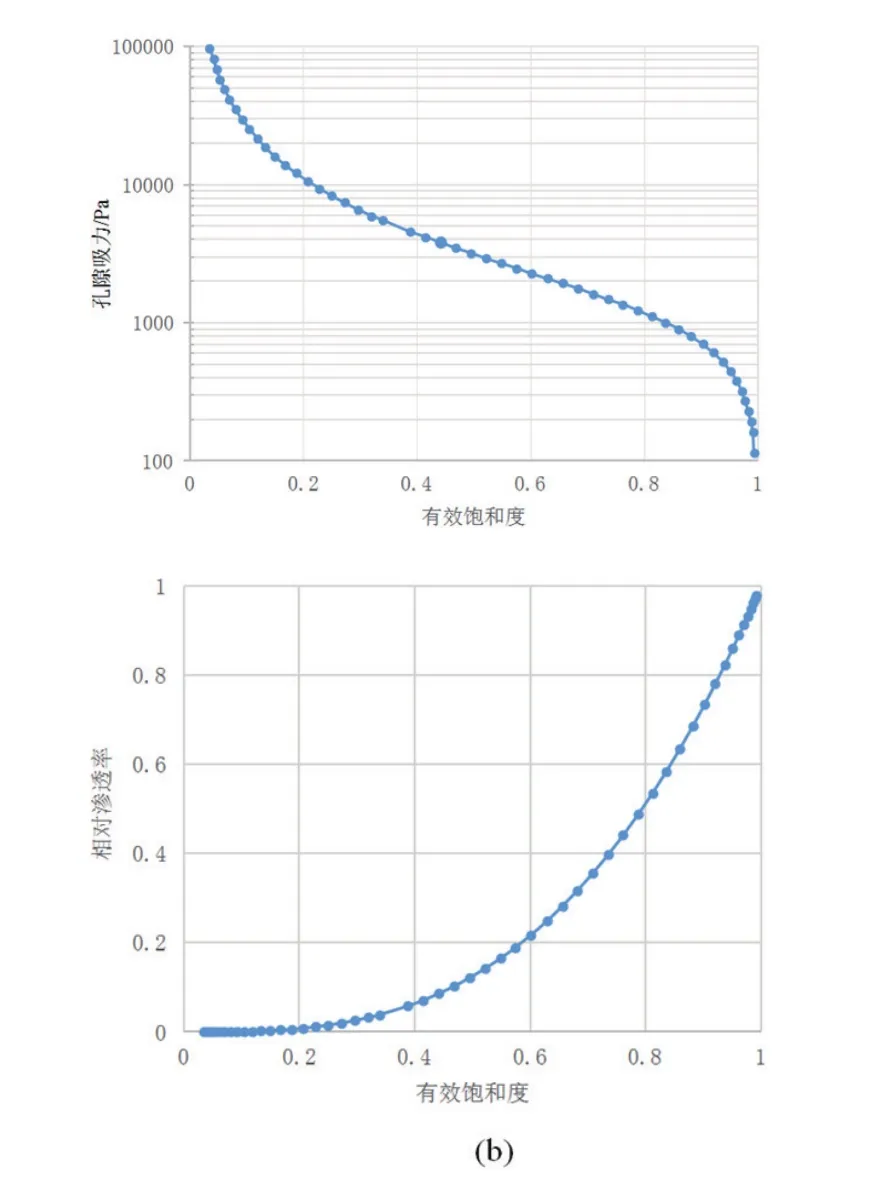
圖2 數值模擬中（a）土水特征曲線；（b）相對滲透率曲線Fig.2 (a)water retention curve; (b)relative permeability curve for the numerical modeling

5 降雨誘發地質災害的數值模擬研究

5.1 初值及邊界條件

參考相關研究成果（王新剛等，2013；胡凱衡等，2014；黃龍波等，2016；陳善雄等，2001；徐晗等，2005；Cho，2016），本次數值模擬中，對三層土分別賦予初值，第一層初始孔隙吸力為48000Pa, 表明第一層土的初始有效飽和度約為0.09；第二層初始孔隙吸力為9000Pa，表明第二層土的初始有效飽和度為0.23；第三層初始孔隙吸力為110000Pa，代表基巖層初始有效飽和度為0.01。

設置環繞模型的曲面在X和Y方向不可移動，即固定曲面在X和Y方向的位移。

為研究降雨強度與堆渣體位移的關系，將降雨強度轉化為模型中的透水量，并假設第一層土的上表面持續降雨入滲，以此為關系變量進行數值模擬計算。

5.2 數值計算結果分析

本研究工作基于單元體積積分計算模型中的透水量，通過定義計算時間步長，得到模型表層的入滲流速。通過GMESH軟件得到模型表層面積為3722.32m2，進一步計算得到降雨強度（mm）。

5.2.1 降雨過程中的流固耦合

降雨入滲過程中的滲流云圖如3所示，圖3(a)為降雨強度達到100mm時的有效飽和度分布云圖。在降雨入滲過程中，堆渣體左右和上方邊界處的有效飽和度逐漸增大，山體中部的有效飽和度增量較小。圖3(b)顯示了第二層土的孔隙水壓力分布云圖和第一層土中的流速分布云圖。由圖3(b)可知，在降雨277mm時，第一層土中山體左右和上方邊界處的流速較大，且由四周匯向中部。

由圖3中可知，由于堆渣體左右和上部區域土層較薄，中部區域土層較厚，由滲透壓力梯度可知，土層厚度越薄，滲透壓力梯度越大，由圖3(b)中可知，降雨277 mm 時周邊區域的滲透驅動力為孔隙水重力。在較大的滲透壓力作用下，孔隙水逐漸流向中部。

綜上可知，在孔隙水壓力的作用下，堆渣體左右和上部邊界區域將發生較大位移。

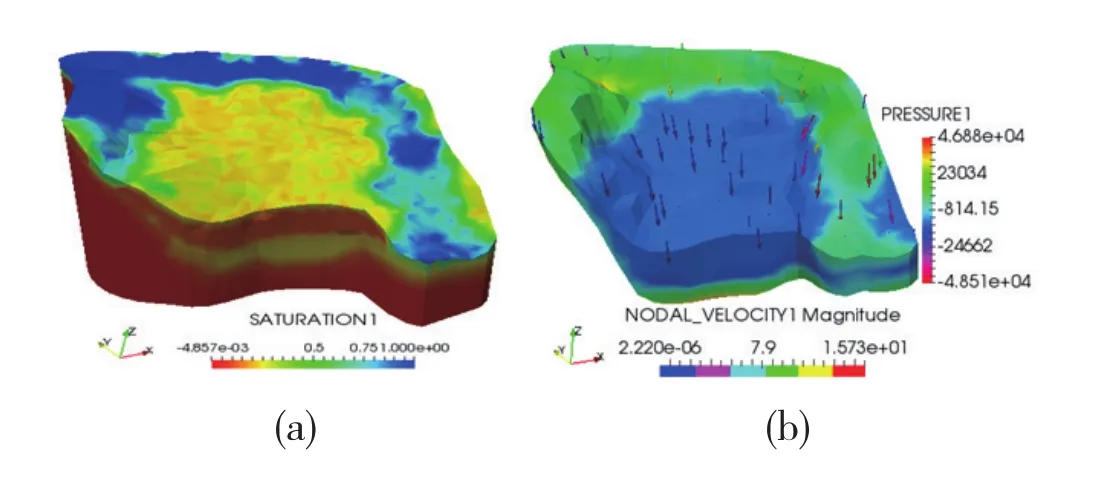
圖3 降雨入滲過程中的滲流云圖(a)降雨100mm時有效飽和度云圖 (b)降雨277mm時流速云圖Fig.3 Seepage diagrams during rainfall inf i ltration(a) Diagram of the effective saturation when rainfall is 100mm(b) Diagram of the fl ow rate when rainfall is 277mm

5.2.2 降雨過程中的應變

降雨入滲過程中堆渣體的應變云圖如4所示。圖4(a)為降雨100mm時堆渣體應變云圖，第一層土的左右和上部坡腳處體應變最大。當降雨達到277 mm時，如圖4(b)所示，山體左右和上部坡面的應變增大。

綜上所述，隨著降雨強度的增大，堆渣體左右坡腳和上部坡面處的體應變不斷增加，并逐漸相互貫通匯成一個較大的滑動帶，且圖3、圖4相互印證，表明降雨的持續入滲是導致堆渣體產生滑移的最重要原因，這有助于為地質災害預警提供依據。

5.2.3 降雨過程中的危險區域判別

根據文獻（黃龍波等，2016；Cho，2016），基于最大剪應力準則，計算堆渣體的剪切強度：

式中：ccritical、φcritical和fcritical分別為與極限剪應力強度相關的粘聚力、內摩擦角和安全系數，τcritical和σs為剪切強度和壓縮強度。取安全系數為1.3，根據表2計算得到第一層土的剪切強度為8.3kPa，第二層土的剪切強度為30.4kPa。

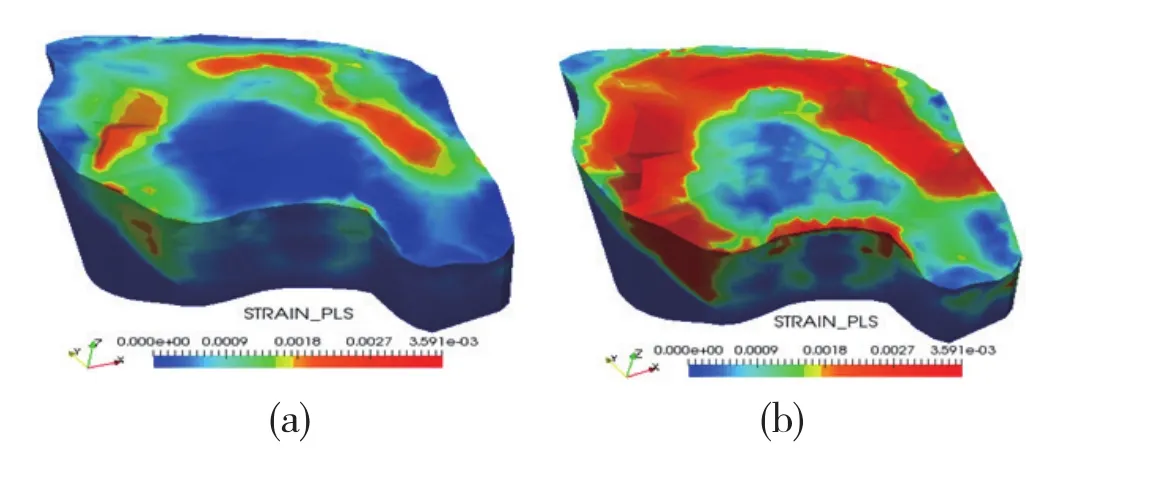
圖4 降雨入滲過程中的應變云圖(a)降雨100mm時的應變云圖 (b)降雨277mm時的應變云圖Fig.4 Strain diagrams during rainfall inf i ltration(a) Strain diagram when rainfall is 100mm (b) Strain diagram when rainfall is 277mm

圖5(a)-(c)顯示了降雨強度在137mm、189mm和277 mm 時的地質災害區域分布圖。圖5(a)中顯示，在降雨累積137mm時堆渣體出現了初始災害，隨著累積降雨量的增加，災害區域開始擴展并逐漸匯集成片，見圖5(b)和(c)。地質災害區域主要發生于陡坡區域，從坡腳向坡面延伸。

本文的數值模擬研究中，不僅考慮了土體孔隙壓力變化導致的有效應力變化，還考慮了堆渣體自重影響下的有效應力變化，圖5的模擬結果表明，基于Mohr-Coulomb屈服準則來判定地質災害危險區域具有可行性和合理性。

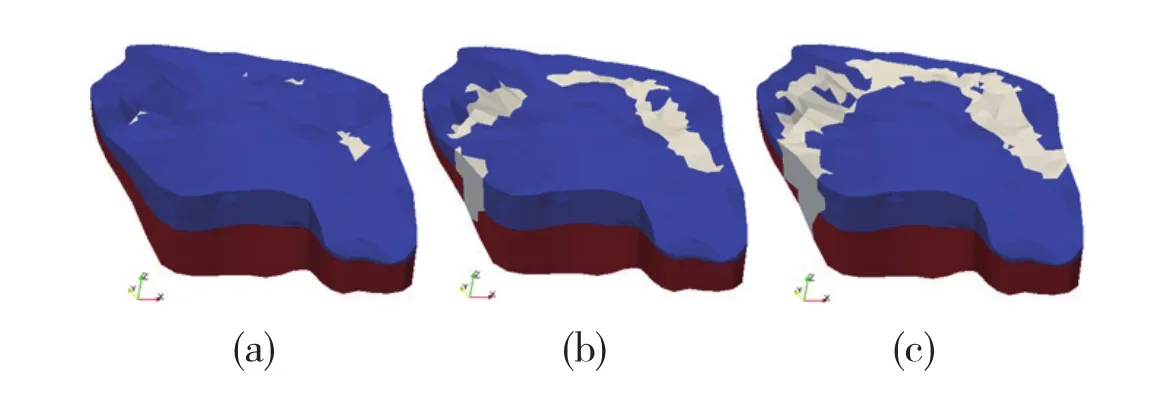
圖5 降雨入滲過程中的災害分布區域(a)降雨137mm時的災害區域 (b)降雨189mm時的災害區域(c)降雨277mm時的災害區域Fig.5 Geology disaster area during rainfall inf i ltration(a) Geology disaster area when rainfall is 137mm (b) Geology disaster area when rainfall is 189mm(c) Geology disaster area when rainfall is 277mm

6 結論

本文在三維地質體展示模型的基礎上進行了有限元網格剖分，并借助于OGS多物理場數值計算平臺，基于有效應力原理、Mohr-Coulomb屈服準則、Richard-flow非飽和滲流方程，對堆渣體在降雨入滲過程中的滲流-應力耦合過程進行了數值模擬研究。研究結果表明：堆渣體左右及上部土層較薄的區域在較大的滲透壓力梯度作用下易產生較大變形，且該處坡面較陡，雨水入滲過程中最易誘發地質災害，其中的主要驅動力有滲透壓力、孔隙水自重和堆渣體土層自重。隨著降雨量增大，有效飽和度增加，受孔隙壓力變化的影響，潛在危險區域逐漸貫通并將發生較大規模的地質災害。

需要說明的是，本文數值模擬中的參數多借助于工程經驗、國內外學者的研究成果等，下一步的工作重點是，在現場實際監測數據的基礎上，合理反演各種力學、滲流參數，以獲得符合北京山區地質特征的流固耦合參數，并進一步預測潛在的危險區域。

Bolzon G, Schrefler B, Zienkiewicz O, 1996. Elastoplastic soil constitutive laws generalized to partially saturated states [J].Géotechnique, 46(2): 279-289.

Cho S E, 2016. Stability analysis of unsaturated soil slopes considering water-air flow caused by rainfall infiltration[J].Engineering Geology, 211: 184-197.

Genuchten M T V, 1980. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of Americal Journal, 44(44):892-898.

Richards L A, 1931. Capillary conduction of liquids through porous mediums [J]. Journal of Applied Physics, 1(5): 318-333.

Terzaghi K V, 1923. Die berechnung der durchlassigkeitsziffer des tones aus dem verlauf der hydrodynamischen spannungserscheinungen [J]. Sitzungsberichte der Akademie der Wissenschaften in Wien, Mathematisch-Naturwissenschaftliche Klasse, Abteilung IIa, 132: 125-138.

陳善雄，陳守義，2001. 考慮降雨的非飽和土邊坡穩定性分析方法[J]. 巖土力學，22(4)：447-450.

董桂芝，紀玉杰，單青生，1997. 北京市地質災害現狀分析[J].北京地質，(1)：30-33.

胡凱衡，馬超，2014. 泥石流啟動臨界土體含水量及其預警應用[J]. 地球科學與環境學報，(2)：73-80.

黃龍波，汪洪星，談云志，等，2016. 降雨對巖土邊坡穩定影響的實例分析[J]. 三峽大學學報（自然科學版），38(4)：40-45.

王新剛，胡斌，劉強，等，2013. 碎石土大型直剪研究與邊坡穩定性分析[J]. 長江科學院院報，30(6)：63-67.

徐晗，朱以文，蔡元奇，等，2005. 降雨入滲條件下非飽和土邊坡穩定分析[J]. 巖土力學，26(12)：1957-1962.

The Application of OpenGeoSys Software in the Geological Disaster Monitoring and Forecast System

DING Jingyang

(Beijing Institute of Geological and Prospecting Engineering, Beijing 100048, China)

Geological disaster is of great treat for the linear project of transportation network. Based on the demonstration project of “Geological Safety Monitoring of Beijing-Zhangjiakou Railway (entrance of Juyong Pass tunnel )”, the fl uid-solid coupling process of a slag heap under the condition of rainfall inf i ltration is researched with the help of OpenGeoSys software, also the theories of effective stress, yield criterion of Mohr-Coulomb and Richard-f l ow equations. The results show that, for the slag heap, the effective saturation of the upper soil increases with the increase of rainfall intensity, also the area of geological disaster is appeared and joined. It provides a basis for the geological safety forecast.

Geological disaster forecast; Rainfall inf i ltration; Fluid-solid coupling; OGS numerical simulation

A

1007-1903（2017）03-0081-06

10.3969/j.issn.1007-1903.2017.03.0016

北京市優秀人才資助項目（2016400617931G171）

丁靖洋（1985- ），男，博士，工程師，主要從事巖土工程研究。E-mail：ak47djy@sina.com