EGM-BP網絡模型在單變量時間序列預測中的應用
——以四川省GDP為例

劉 攀，馮長煥

（西華師范大學，四川 南充 637002）

EGM-BP網絡模型在單變量時間序列預測中的應用
——以四川省GDP為例

劉 攀，馮長煥

（西華師范大學，四川 南充 637002）

利用GM(1,1)模型需要的數據少，而BP網絡模擬精度高且適合非線性系統的特點，基于GM(1,1)模型的均值形式，以1980—2016年四川省GDP值作為原始序列，其累加序列、均值序列和前一歷史序列作為輸入向量，原始序列作為輸出向量，進行BP網絡訓練，建立EGM-BP網絡模型，提出了一種灰色神經網絡的新方法。利用2014—2016年的GDP數據進行驗證，發現EGM-BP模型對于單變量時間序列預測的精度比傳統單一模型預測精度更高。

GM（1,1）模型；BP神經網絡；單變量時間序列；GDP預測

0 引言

GDP（Gross Domestic Product）是指一個國家或地區所有常駐單位在一定時期內生產活動的最終市場價值。它反映了一個國家或地區一定時期內的經濟實力和市場規模狀況，是國民經濟核算體系的核心指標。精準地預測GDP不僅能加強國家宏觀調控，而且能促進企業經營管理，使得經濟決策科學化。國內學者對GDP數據預測的研究成果頗多，建立的數學模型主要有回歸模型、指數平滑模型、灰色GM（1，1）模型、ARIMA 模型、神經網絡模型以及它們的組合模型[1-4]。

神經網絡近年來在數學、物理、工程等領域的應用十分廣泛，并涌現了大量的成果。BP網絡是使用最廣泛的一種神經網絡，它通過建立從輸入到輸出的映射關系，在自動學習之后，能在一定條件下以任意精度實現任意的非線性映射。BP網絡需要一定數量的訓練樣本才能作較好的預測。灰色GM（1，1）模型對數據的要求較少，但不能直接用于非齊次指數序列和振蕩序列的建模。筆者把GM（1，1）模型和BP網絡結合，建立EGM-BP網絡模型，該模型同時具有GM（1，1）和BP網絡的特點，能在較少信息量的情況下對未來時間序列作出較好的預測。

本文把1978—2016年四川省GDP值作為原始序列，利用灰色GM（1，1）模型中累加生成和均值生成的思想，生成與原始序列相關的3組序列，以此作為輸入向量。把原始GDP值作為輸出向量，構建了結構為3-6-12-1的BP網絡。利用2014—2016年的GDP數據進行模型精度的比較，結果表明EGMBP網絡模型比傳統單一模型誤差更小，精度更高。

1 模型的原理和方法

1.1 EGM（1，1）模型

灰色系統理論由鄧聚龍教授在1982年創立，目前已被廣泛應用于自然科學、社會科學、工程技術等各個領域。GM（1，1）模型是灰色系統理論的核心部分，它有4種基本形式：均值形式（EGM）、原始差分形式（ODGM）、均值差分形式（EDGM）和離散形式（DGM）。人們提到的 GM（1，1）模型通常是指EGM（1，1）[5]。EGM（1，1）通過建立關于原始序列的特殊差分方程和微分方程，在一定程度上模擬單變量時間序列，能對未來時間序列做出預測。

EGM（1，1）的建模步驟如下：

設原始序列 X ( 0) = (x (1),x (2),???,x (n ))，x（0）（k）≥0，k=1，2，…，n。記 X（0）的累加序列為 X（1）=（x（1（）1），x（1）（2），…，x（1）（n）），記X（1）的緊鄰均值序列為Z（1）=（z（1）（1），z（1）（2），…，

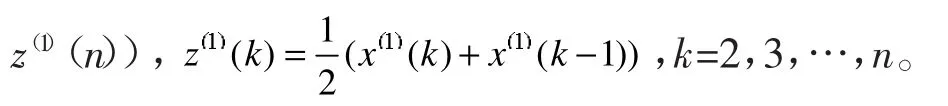
（1）建立白化微分方程：

其中a，b滿足差分方程：

稱 a 為發展系數，b 為灰色作用量，z（1）（k）為灰色背景值。

（2）利用最小二乘法求參數向量 a^ = [a, b]=（BTB）-1BTY，其中 BT，Y 分別為：

得到白化微分方程的解（也叫EGM（1，1）模型的時間響應式）：

（3）求累減還原式，得到原始序列的模擬表達式：

1.2 BP網絡模型

BP網絡(Back-Propagation Network)，即反向傳播網絡，由Rumelhart等人在1986提出，是目前使用最廣泛的神經網絡模型[6]。BP網絡在函數逼近、模式識別、數據的壓縮與分類等方面得到了大量的應用。

其模型的思想為：建立一個三層或三層以上的神經網絡（輸入層、隱層和輸出層），使數據從輸入層向隱層傳輸，隱層向輸出層傳輸。層與層之間由激勵函數和權值連接，在數據傳輸的過程中，通過誤差的反饋，不斷地反向調整各層之間的連接權值，直至達到指定的精度或運算次數。

MATLAB軟件構建BP網絡的步驟[6，7]：

（1）網絡結構的設置

BP網絡結構由輸入層、隱層和輸出層構成，隱層至少為一層。根據Kolmogorov定理，一個三層的前饋神經網絡能以任意精度逼近任意連續的函數[7]。隨著網絡層數的增加，誤差進一步降低。但這也會增加網絡的復雜性和學習時間。所以，一般不增加網絡的層數，而是通過增加隱層神經元的個數來嘗試降低誤差，提高精度。

（2）輸入層和輸出層的設置

輸入向量為影響待預測序列的主要因素序列，輸入層節點為主要因素的個數。輸出向量為需要預測的序列，其節點數為待預測序列的個數。為了消除量綱的影響以及提高網絡學習的收斂性，通常需要對數據作歸一化處理，把數據規范在[-1,1]或[0,1]區間內。

（3）隱層節點的設置

目前，關于隱層節點的設置還沒有一個具體的公式來確定，一般使用試湊法及以下經驗公式[6]來確定：

3） N = l ogn ，其中n為輸入層節點數。

（4）網絡參數的設置

在MATLAB中，使用newff函數創建一個BP網絡。層與層之間的激勵函數主要有S型對數函數(logsig)、S型正切函數(tansig)和純線性函數(purelin)等。BP網絡訓練函數默認為L-M算法訓練函數(trainlm)。期望誤差的學習目標默認為0，可以根據需要設置學習目標的精度。迭代次數一般不超過50000次。學習效率在0到1之間，并不是越大或越小越好，太大使系統不穩定，太小會使訓練時間過長。

（5）網絡訓練與檢驗

（6）預測與誤差分析

1.3 EGM-BP網絡模型

（一）EGM-BP網絡模型的原理

（二）EGM-BP網絡模型主要步驟

（1）設原始序列 X（0）=（x（0）（1），x（0）（2），…，x（0）（n））,X（0）（k）≥0，k=1，2，…，n；

（2）計算X（0）的前一歷史序列X'（0）、累加序列 X（1）、以及 X（1）的緊鄰均值序列為 Z（1）；

（3）把X'（0）、X（1）、Z（1）作為輸入向量，X（0）作為輸出向量，構建BP網絡；

（4）網絡訓練與檢驗；

（5）預測與誤差分析。

2 實證分析

2.1 數據的選取

本文選取1978—2016年四川省GDP數據為研究對象（單位為億元），數據來源于四川統計局。以2014—2016年的數據作為檢驗數據。

記1980—2016年的原始GDP值為輸出向量T0=［t（1），t（2），…，t（37）］。分別記T0的累加序列、累加序列的均值序列、前一歷史序列為pi（i=1，2，3），記輸入向量 p0=［p1；p2；p3］。

2.2 EGM-BP網絡模型步驟

（1）網絡結構、輸入層和輸出層的設置

本文選擇建立四層BP網絡，由T0和P0知，輸入和輸出層節點分別為3和1。由于S型激勵函數的輸出值只能無限接近0或者1，而不能達到0或者1，為了增強網絡的泛化能力，本文把數據規范在[0.1,0.9]區間內。歸一化的方法是其中M和m分別為該序列的最大值和最小值。

（2）隱層節點的設置

本文采用試湊法，得出適合的兩個隱層節點數分別為6和12，相應的BP網絡結構為3-6-12-1。

（3）網絡參數的設置

通過反復試驗，得到適合的網絡參數見表1。其他參數選擇MATLAB默認設置。

表1 EGM-BP網絡模型參數設置

（4）網絡訓練

（5）網絡的檢驗與預測

利用2014—2016年四川省GDP數據對模型進行精度檢驗，結果見表2。結果顯示，預測值與實際值的相對誤差的絕對值都在0.3%以內，誤差較小。

2017年四川省GDP的前一歷史值為32680.5億元，累積值為284519.71億元，累加值的均值生成為268179.46億元。把這三個值作為輸入向量，得到2017年四川省GDP的預測值為35008.87億元。相對2016年的增速約為7.12%，與四川省2017年1季度GDP實際增長接近。

表2 EGM-BP網絡模型檢驗結果

3 其他模型結果的對比

3.1 基于時間的曲線擬合模型

記1980—2013年四川省GDP值為y，時間t=1，2，…，34。分別對y關于t作一次曲線、二次曲線、三次曲線擬合，結果顯示三次曲線的擬合度最高，為0.991。擬合曲線為：

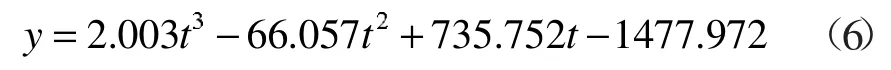
由于1980—2013年四川省GDP呈近指數增長，分別對y關于t作S型曲線、生長曲線擬合，生長曲線的擬合度最高為0.995。擬合曲線為：

3.2 GM（1,1）模型

由于舊信息歷史久遠，與新信息的相關程度可能不高，新信息顯得更重要，因此建立灰色新陳代謝模型。分別建立4至10階GM（1，1）模型，結果表明，4階GM（1，1）模型的誤差最小，其結果見表3和表4。

3.3 BP網絡模型

針對1980—2013年四川省GDP數據，把年份作為輸入向量，原始GDP作為輸出向量，建立BP網絡，結果見表3和表4。

表3 傳統單一模型預測結果

表4 傳統單一模型預測相對誤差

4 結語

四川省作為西部人口大省，科學地預測其GDP總量對于政府制定經濟政策和企業規劃有重要的意義和價值。預測結果表明2017年四川省GDP總量將持續增加，增長率將在7.12%左右。基于GM（1，1）模型的累加生成和均值生成的思想，結合BP網絡，本文建立了EGM-BP網絡模型，實驗結果表明，EGM-BP模型比傳統單一模型效果更好，精度更高。本文提出的EGM-BP模型還可用于其他單變量時間序列的預測。另外，人工神經網絡中其他網絡也具有良好的預測功能，如RBF網絡、Elman網絡、小波神經網絡等，后續研究可考慮將累加生成和均值生成的思想與這些網絡結合進行科學預測。

［1］龍會典，嚴廣樂.基于 SARIMA、GM（1，1）和 BP 神經網絡集成模型的GDP時間序列預測研究［J］.數理統計與管理，2013，32（5）:814-822.

［2］許金煒.基于虛擬變量回歸與SARIMA組合模型的GDP預測［J］.統計與決策，2016，（24）:38-41.

［3］薛倩,牟鳳云,涂植鳳.組合預測方法在重慶市 GDP預測中的應用 ［J］.重慶工商大學學報 （自然科學版），2017，34（1）:56-63.

［4］龍會典,嚴廣樂.基于改進的 GM（1，1）-Markov鏈組合模型廣東省單位GDP能耗預測［J］.數理統計與管理，2017，36（2）:200-207.

［5］劉思峰，謝乃明，等.灰色系統理論及其應用（第六版）［M］.北京：科學出版社，2013:97-121.

［6］飛思科技產品研發中心.神經網絡理論與MATLAB7實現［M］.北京：電子工業出版社，2005:99-107.

［7］施彥，韓力群，廉小親.神經網絡設計方法與實例分析［M］.北京：北京郵電大學出版社，2009:23-36.

EGM-BP Network Model in the Application of Single Variable Time Series Prediction——Taking Sichuan GDP as Example

LIU Pan,FENG Chang-huan
（China West Normal University，Nanchong 637002,China）

GM(1,1)model requires less data and BP network modeling is of high accuracy and suitable for the nonlinear systems.Thus，based on EGM(1,1)model，the GDP value of Sichuan Province from 1980 to 2016 was set as the original series,then its cumulative series，average series and the series of previous historical period was set as input vector，and the original series was set as the output vector to conduct the BP network training.EGM-BP network model was set up，proposed a new method for gray neural network.In the 2014-2016 GDP data verification，the results showed that EGM-BP model for single variable time series had higher precision than traditional single model.

GM(1,1)；BP neural network；single variable time series；GDP forecast

F224

A

1674-3229（2017）03-0008-04

2017-06-03

西華師范大學基本科研項目(14C004)；南充市社科規劃一般規劃項目（NC2013B027)

劉攀(1995-)，男，西華師范大學碩士研究生，研究方向：應用數理統計；馮長煥（1972-），女，碩士，西華師范大學數學與信息學院教授，研究方向：應用數理統計。