某客車動力總成懸置系統優化設計

曾發林，潘 偉，李建康，阮 洋

(江蘇大學 a.汽車工程研究院; b.汽車與交通工程學院， 江蘇 鎮江 212013)

某客車動力總成懸置系統優化設計

曾發林a，潘 偉b，李建康a，阮 洋b

(江蘇大學 a.汽車工程研究院; b.汽車與交通工程學院， 江蘇 鎮江 212013)

根據某款6902型客車懸置系統測量的各項參數，建立動力總成懸置系統6自由度的動力學模型。運用能量解耦法及NAGA-II優化算法，先基于正交試驗方法對動力總成懸置系統剛度參數進行靈敏度分析，然后以動力總成懸置系統的6個方向耦合度為設計目標、6個懸置元件的三向主剛度參數為設計變量，對動力總成懸置系統進行優化設計。結果表明：經過優化后的懸置系統有效地提高了各向解耦率，實現了固有頻率的合理配置，改善了懸置系統的隔振性能，提高了汽車乘坐舒適性。

懸置系統；能量解耦；靈敏度分析；隔振

Abstract: According to the parameters of a 6902 type passenger car suspension system measurement, we establish dynamic model of the powertrain mounting system of 6 degrees of freedom. By using the energy decoupling method and NAGA-II optimization algorithm, first based on orthogonal test method, we has the sensitivity analysis of system stiffness parameters for powertrain mounting, and taking the 6 directions of coupling of powertrain mount system as the design goal, taking three main stiffness parameters of 6 directions as design variables, the powertrain mounting system was optimized.The experimental results show that after optimization, the suspension system can effectively improve the anisotropy of the decoupling rate and achieve the reasonable allocation, the natural frequency, which improves the isolation performance of the mounting system, and improves the ride comfort of the car.

Keywords: mounting system; energy decoupling; sensitivity analysis; vibration isolation

隨著生活質量的提升和現代汽車技術的發展，人們不僅追求車輛的動力性、安全性、燃油經濟性，而且對汽車的乘坐舒適性的要求也越來越高[1]，使我們在汽車設計中對懸置系統的設計提出了越來越高的指標。通過選擇適當的懸置系統參數(安裝位置、角度和剛度等)，可達到合理配置動力總成剛體振動模態的固有頻率和實現系統振動解耦是懸置系統設計的基本任務[2]。

本文以某款6902型客車為研究對象，在動力總成懸置系統振動分析的基礎上，以6個懸置元件的3個方向主剛度為設計變量，以動力總成懸置系統的振動能量解耦為目標函數，選擇系統Z向的振頻在2.5～10 Hz范圍內作為形態約束條件，將Isight優化軟件與Matlab軟件集成，提出了車輛懸置系統的優化方法，最后對動力總成懸置系統進行了隔振率性能的測試，對優化前后結果進行了對比分析。

1 動力懸置系統模型

本文根據所研究的6902型客車動力總成懸置系統的各項參數，得到懸置系統的簡易模型：由6個具有3個主方向的彈簧阻尼元件支撐在車架上的6自由度振動系統。圖1為6個懸置元件的分布情況。動力總成坐標原點在其重心處；X軸平行于曲軸中心線，指向動力總成飛輪；Z軸平行于氣缸中心線，指向動力總成上方；Y軸則由正交坐標系的右手定則確定。

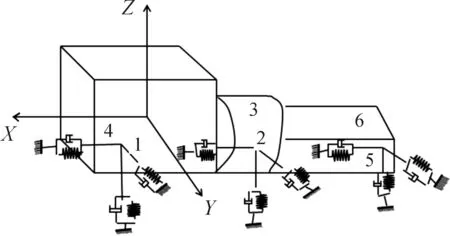
圖1 6點式布置的動力總成懸置系統模型

動力總成懸置系統6自由度振動的一般形式為[3]:

(1)

其中：T為系統的動能；V為系統的勢能；qi為系統的廣義坐標。

對上述動力總成懸置系統力學模型可以建立6自由度無阻尼自由振動方程：

(2)

由式(2)可得到系統的主振型方程|K-ω2M|=0，計算得到系統的6階固有頻率和ωj(j=1,2,3,4,5,6)固有振型{φ}。

2 能量解耦法

能量解耦法是從能量角度實現各自由度的解耦[4]。如一空間剛體僅做垂直自由振動而和其他自由度解耦時，其振動能量只集中于垂直方向自由度上。當系統以第j階模態振動時，第k個廣義坐標分配的能量占系統總能量的百分比為

當Eji=100%，系統作第j階模態振動時能量全部集中在第i個廣義坐標上，此時該階模態振動完全解耦。

3 優化算法

本文采用MOP多目標優化理論[5]，對于有n個變化量，m個目標函數，q+p個約束條件的MOP可表達為：

其中：x=(x1,x2,…,xn)T∈X?Rn為n維決策變量，X為n維空間決策；y=(y1,y2,…,ym)T∈Y?Rm為m維目標矢量，Y為m維目標空間；gi(x)≤0(1,2,…,q)定義了q個不等式約束；hj(x)=0(j=1,2,…,p)定義了p個等式約束[6]。

NSGA-II是基于遺傳算法的非支配排序算法，其原理是根據個體之間的支配關系調用每個目標函數，使每個目標函數都盡可能達到pareto解[7]。在MOP算法(PSO、GA、NSGA、ACO等)中，NSGA-II算法是影響最大和應用范圍最廣的一種多目標遺傳算法，且具有很好的魯棒性和收斂速度。因此，本文采用NSGA-II算法解決動力懸置系統的優化問題。NSGA-II算法的基本流程如圖2所示。

圖2 NSGA-II算法的主流程

4 動力總成懸置系統模型準確性驗證

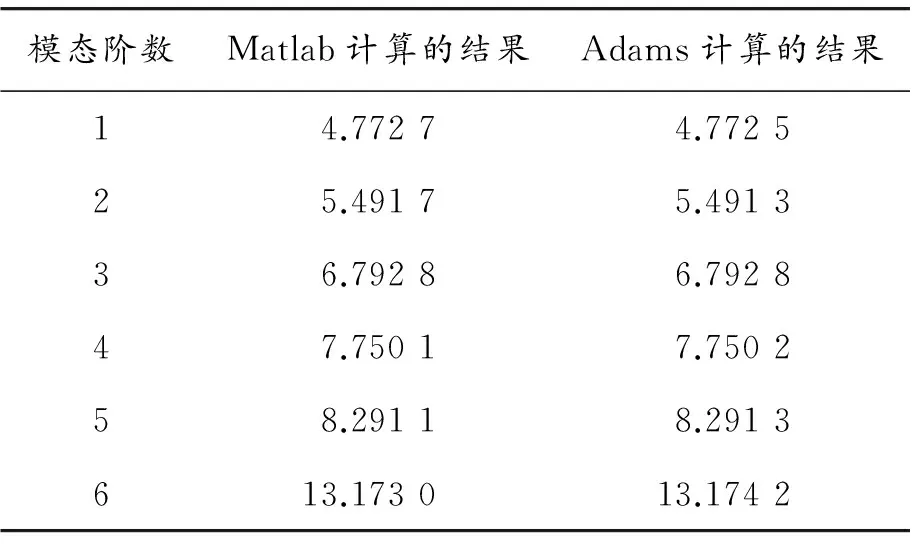
筆者采用試驗模態方法識別客車的動力總成慣性參數，以某企業提供的PRO/E 和CAD模型為參考，結合對動力總成實際的測量，建立了動力總成懸置系統的動力學模型，如圖3所示。由于懸置系統的動力學模型的準確性對頻率特性和解耦特性分析和優化設計結果的精確度影響很大，那么模型的搭建是其解耦及優化設計的關鍵，因此有必要對模型的準確度進一步驗證。在Matlab軟件中編制程序，按照振動微分方程，利用Matlab算出動力總成懸置系統理論上的固有頻率，結果如表1所示。在ADAMS中的VIEW模塊庫中調用自帶的BUSHING來模擬橡膠懸置元件，在ADAMS/vibration模塊中分析動力總成懸置系統的固有頻率[2]，結果如表1所示。懸置元件的初始參數如坐標位置、慣量參數和初始剛度如表2、3和4所示，動力總成的總質量為1 261 kg。

圖3 基于ADAMS/view的動力總成懸置系統動力學模型

模態階數Matlab計算的結果Adams計算的結果14.77274.772525.49175.491336.79286.792847.75017.750258.29118.2913613.173013.1742

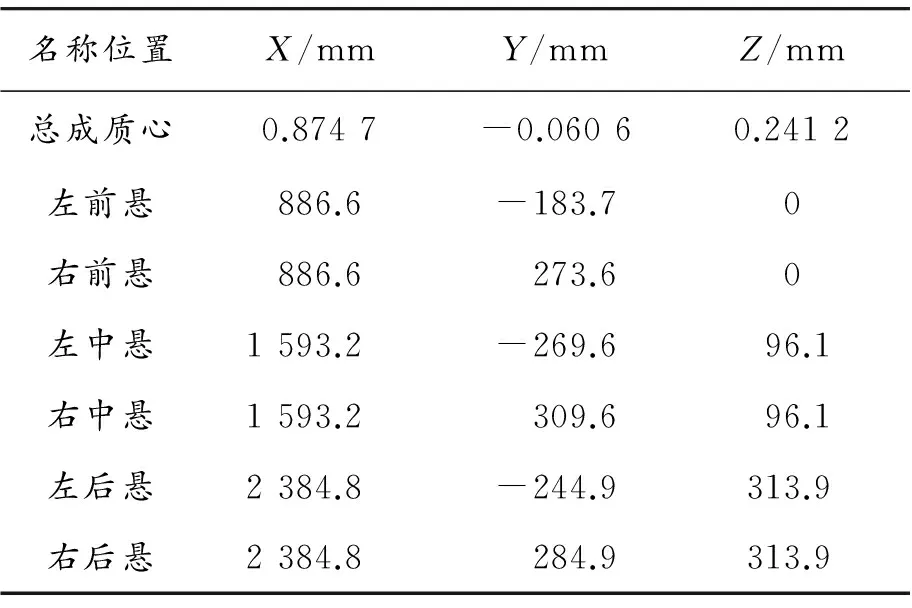
表2 懸置元件及動力總成的坐標位置

表3 動力總成的慣量參數

兩種計算固有頻率的結果如表4所示。

從兩組數據的對比可知，動力總成懸置系統的固有頻率基本吻合，所以可以認為所建立的動力總成懸置系統6自由度動力學模型是正確可靠的，可以用來進行解耦與優化設計。

表4 優化前原懸置各向剛度

5 動力總成懸置系統優化

5.1 優化設計變量和靈敏度分析

工程實踐中，主要考慮調整系統兩個方面的參數：懸置件的主剛度及其安裝位置[8]，而本例中懸置位置和安裝角度受整車布置限制都已確定，故只選取了各個懸置件的主軸剛度值作為設計變量。因為有6個懸置件，計共有18個設計變量，如表5所示。考慮到在影響動力總成懸置系統解耦特性頻率特性的這些變量參數中，某些變量對目標函數比較敏感，而某些變量對目標函數沒有任何影響[9]，所以筆者基于正交試驗對動力總成懸置系統的三向主剛度參數進行靈敏度分析，找出影響程度大的主要變量參數，減少次要的設計變量，然后基于主要變量參數，在Isight中進行多目標優化，表6為靈敏度分析之后的影響變量。

5.2 目標函數

由能量解耦法可知，某一階頻率下，當沿某一方向的振動動能百分比達到100%時，懸置系統在該頻率下是完全解耦的，但對于激勵源復雜的動力總成懸置系統是不可能實現完全解耦的，肯定存在個別方向的振動耦合，這里只能盡可能使占優方向的振動動能比最大。筆者以6個能量解耦率為目標函數，見表7所示。

表5 靈敏度分析前的設計變量參數

表6 經過靈敏度分析后的設計變量

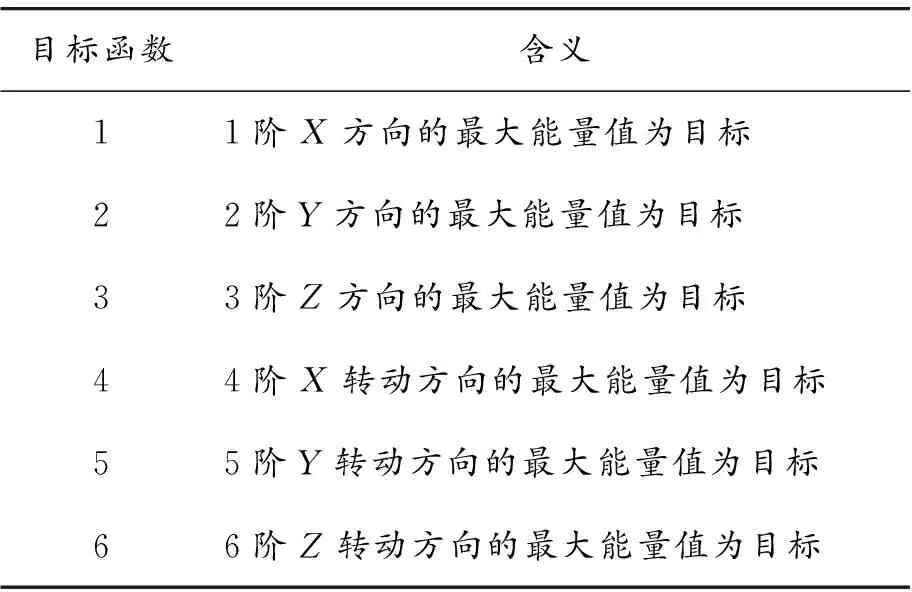
表7 優化的目標函數

5.3 約束條件

在求Pareto解中，尋優是在所有約束條件構成的可行域中完成。在優化設計中一般存在兩種約束條件：一種是邊界限制條件，另一種是形態限制條件，筆者選擇懸置系統Z向的振頻在2.5～10 Hz 范圍內作為形態限制條件。

5.4 優化算法

在優化過程中，采用NSGA-II算法，參數設置為：變量的范圍為+/-100%,種群規模為100，預設進化代數為100，交叉概率為0.9，變異概率為0.1，交叉分布指數為10.0，突變分布指數為20.0，采用Isight與Matlab集成優化。

5.5 優化前后結果對比

將分析的動力總成懸置系統的參數和動力學模型，在ADAMS/vibration模塊中計算懸置系統的解耦率[10]，分析它的振動耦合情況，結果如表8所示。

由表8可知，此方案存在嚴重的耦合，繞Z向的轉動和Z向平動的耦合程度很大，且X向平動耦合率62%，繞Y向轉動67.76%，均未達到工程上可以接受的80%，而Y向的平動與繞X向的轉動的解耦率都達到了90%以上。在解耦率較低的情況下，惡化動力總成懸置系統的隔振性能，同時降低了動力總成懸置元件的耐久性。因此，需要對其進行優化設計，以減少其振動耦合，提高其隔振性能。表9為經過優化后的懸置系統的剛度。

表9 優化后的懸置剛度

將優化后的剛度參數賦予到建立的動力總成懸置系統模型中，在Adamas中計算其固有頻率和解耦率，結果如表10所示。

表10 優化后懸置系統固有頻率和能量分布比

從表10可知，相對于原始剛度值，左前懸置X、Y、Z方向剛度值有所增加，左、右中懸置X方向剛度值減小較大，左、右中懸置Y、Z方向剛度值有所增大。優化后各方向的解耦率都達到了90%，滿足設計要求。

5.6 實車測試

懸置系統并不是汽車中獨立的振動系統，單獨分析懸置系統的優化結果只是停留在它的理論階段，為此，我們根據優化后的懸置系統，在某客車上進行實車振動測試，以測得的懸置隔振率來論證優化后懸置系統的隔振性能。

在評價懸置隔振效果時，最常用的評價指標是懸置隔振率。汽車業內認為動力總成懸置系統的隔振率應大于20 dB，懸置才具有良好的隔振效果[11]。懸置隔振率以分貝形式表示，計算公式如下：

(3)

式中：aactive為主動邊振動的加速度均方根值；apassive為被動邊振動的加速度均方根值。

本試驗以某6902型客車為例，分別測出原懸置和優化后懸置從怠速到最高轉速共5種工況下各測點的振動信號，即(怠速、1 000、1 500、2 000、2 500 r/min)，部分懸置傳感器安裝位置如圖4所示。

圖4 部分傳感器布置位置

將優化前后計算好的振動隔振率繪制成曲線進行對比，結果如圖5～10所示。

圖5 左前懸置優化前后隔振率

圖6 左中懸置優化前后隔振率

圖7 左后懸置優化前后隔振率

圖8 右前懸置優化前后隔振率

圖9 右中懸置優化前后隔振率

圖10 右后懸置優化前后隔振率

由圖5～10可知：左前、左中、右中懸置在怠速時不同工況下懸置元件的隔振率都達到20 dB；右前、右后懸置在怠速時部分工況下懸置元件的隔振率在19 dB左右；左后懸置元件的隔振率在17 dB左右。但總的來說，6個懸置元件在優化后的隔振率比優化前要好。

6 結束語

1) 在優化之前，對以6個懸置元件的3個方向主剛度值為設計變量進行靈敏度分析，剔除低靈敏度的設計變量，只考慮敏感設計變量，大大提高了優化效率。

2) 優化后懸置系統各方向的解耦率都得到了提高，達到了90%以上。

3) 根據試驗數據可知：優化后的懸置隔振率大部分得到提高，即系統總體隔振性能得到改善，比優化前要好，優化后的懸置系統基本滿足隔振要求，提高了汽車乘坐舒適性。

[1] 龐劍,何華.汽車噪聲與振動_理論與應用[M].北京：北京理工大學出版社,2006.

[2] 童東紅,郝志勇.動力總成懸置系統優化及穩健性分析[J].汽車技術，2014(2)：19-23.

[3] 付江華,史文庫,沈志宏，等.基于遺傳算法的汽車動力總成懸置系統優化研究[J].振動與沖擊,2010(10)：187-190.

[4] 王天利,孫營，等.基于能量法解耦的汽車動力總成懸置系統優化[J].機械設計與制造,2006(7)：31-34.

[5] BURGESS P.Lexus RX300-luxury on the off-road[J].Automotive Engineering,2001,26(1):74-78.

[6] 賴宇陽.Isight參數優化理論與實例詳解[M].北京：北京航空航天大學出版社,2012.

[7] 段緒偉,李以農,鄭玲,等.基于NSGA-II遺傳算法的磁流變懸置多目標優化[J].振動與沖擊,2014(3):191-196.

[8] 吳杰,李軾.某轉載機動力總成懸置系統隔振性能優化[J].振動與沖擊,2016(1)：23-27.

[9] 任露泉.試驗優化技術[M].北京：機械工業出版社，1987.

[10] 鄭建榮.虛擬樣機技術入門與提高[M].北京：機械工業出版社,2002.

[11] 方錫邦,陳樹勇,張文矩.轎車動力總成懸置系統隔振性能的仿真研究[J].合肥工業大學學報,2003,26(2)：236-241.

(責任編輯何杰玲)

OptimizationDesignofPowertrainMountingSystemofaBus

ZENG Falina, PAN Weib, LI Jiankanga, RUAN Yangb

(a. Automotive Engineering Research Institute; b.School of Automobile and Traffic Engineering, Jiangsu University, Zhenjiang 212013, China)

2016-03-10

江蘇省普通高校研究生科研創新計劃項目(CXLX12_0630)

曾發林(1963—)，男，江蘇鎮江人,副教授，主要從事汽車NVH研究，E-mail:519491781@qq.com。

曾發林，潘偉，李建康，等.某客車動力總成懸置系統優化設計[J].重慶理工大學學報(自然科學)，2017(9):29-35.

formatZENG Falin, PAN Wei, LI Jiankang,et al.Optimization Design of Powertrain Mounting System of a Bus[J].Journal of Chongqing University of Technology(Natural Science)，2017(9):29-35.

10.3969/j.issn.1674-8425(z).2017.09.005

U271.91

A

1674-8425(2017)09-0029-07