某渦輪增壓器殼體熱應力分析

曹良丹　于艇　沈棟平　周唯儒

基于數值傳熱學基本理論，本文建立了某型號渦輪增壓器殼體有限元模型，采用Abaqus/CAE軟件對渦輪增壓器殼體進行瞬態熱應力分析，計算中熱邊界條件隨工作循環的變化趨勢由試驗提供；仿真獲得了渦輪殼體瞬態溫度場和熱應力分布，溫度場分布在第二個工作循環后趨于穩定，對后續快速計算渦輪殼體結構分析提供了方法；進而計算出渦輪殼體關鍵部位等效塑性應變（PEEQ）分布，并對渦輪殼體的熱機械疲勞進行了初步評估。

一、前言

渦輪增壓器主要由渦輪機和壓氣機等構成，其將發動機排出的廢氣引入渦輪機，利用廢氣的能量推動渦輪機旋轉，由此驅動與渦輪同軸的壓氣機實現增壓。渦輪機進氣口與發動機排氣歧管相連，排氣口則接在排氣管上；壓氣機進氣口與空氣濾清器相連，排氣口則接在進氣歧管上。

渦輪增壓器工作過程中，渦輪殼體總是承受隨發動機曲軸轉角變化而變化的溫度載荷，在交變溫度和交變應力的耦合作用下，渦輪殼體不斷累積的塑性變形容易導致裂紋萌生、擴展甚至斷裂。所以本文對渦輪殼體在交變溫度載荷作用下的應力及應變分布進行仿真，進而對渦輪殼體的熱機械疲勞進行了初步評估和預測，這對實際工程應用具有重要作用和重大的指導意義。

二、幾何模型

本文以某型號渦輪增壓器殼體為研究對象，利用CATIA軟件生成三維幾何模型，如圖1所示。熱量主要以熱傳導、熱對流和熱輻射三種方式進行傳遞，結合渦輪增壓器工作原理、結構組成等特點，此次仿真中忽略熱輻射對其溫度及熱應力的影響，故部件熱量傳遞路徑為：（1）渦輪增壓器殼體內流體與殼體的強制對流換熱；（2）殼體部件內部的導熱換熱；（3）渦輪增壓器殼體與外界流體的強制對流換熱。

三、有限元計算模型和邊界條件

1.有限元計算模型

本文利用Hypemesh軟件進行前處理，對圖1所示幾何模型進行處理（添加底座、螺栓及連接板部件，以便施加實際與渦輪殼體相作用的載荷和邊界條件）和簡化（去掉不重要小特征）；渦輪殼體剖分四面體網格，底座、螺栓及連接板部件剖分六面體網格，節點總數約為20.1萬，網格總數約為77.5萬；并對渦輪殼體各部分分區處理，以便施加試驗所給各區熱邊界條件；建立完成的有限元計算模型如圖2所示。

2.邊界條件

本文在Abaqus/CAE中創建邊界條件，螺栓與渦輪殼體表面接觸摩擦系數為0.2，螺栓預緊力為11.5kN，靠近渦輪殼體的連接板孔施加剛性耦合約束，連接板兩外孔和底座底部施加固支邊界條件；渦輪殼體內外流場溫度和對流換熱系數隨時問的變化趨勢如圖3和圖4所示；渦輪殼體材料為1.4837+Nb，其彈性模量、屈服強度、導熱系數和熱膨脹系數等材料參數隨溫度的變化關系由供應商提供。

四、計算結果及分析

本文選用Abaqus/Standard求解器求解，創建Coupled temp-displacement（transient）分析步進行直接耦合熱應力分析，由于幾何存在大變形，故仿真中打開幾何非線性；仿真獲得了渦輪殼體在不同時刻的溫度場、應力場及等效塑性應變（PEEQ）分布圖，依據PEEQ變化趨勢對結構熱疲勞進行初步評估和預測。

1.330s時刻渦輪殼體溫度場、應力場及等效塑性應變結果

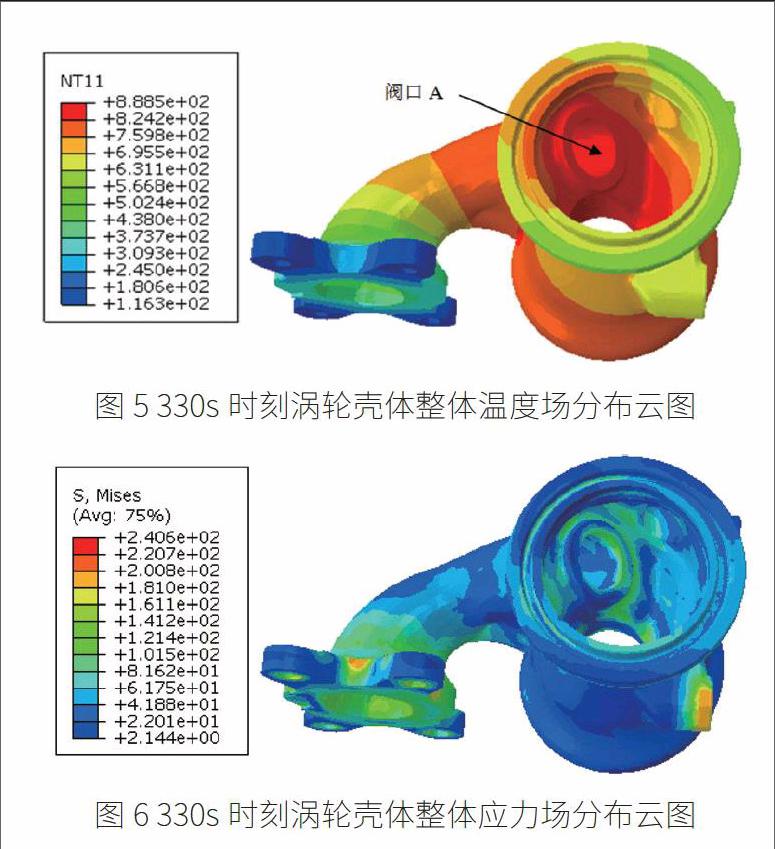
圖5所示為一個工作循環結束（330s時刻）渦輪殼體整體溫度場分布云圖，由圖5可知：殼體最高溫度為888.5℃，高溫區域主要分布在閥口A附近；圖6為一個工作循環結束（330s時刻）渦輪殼體整體應力場分布云圖，最大應力為240.6MPa。

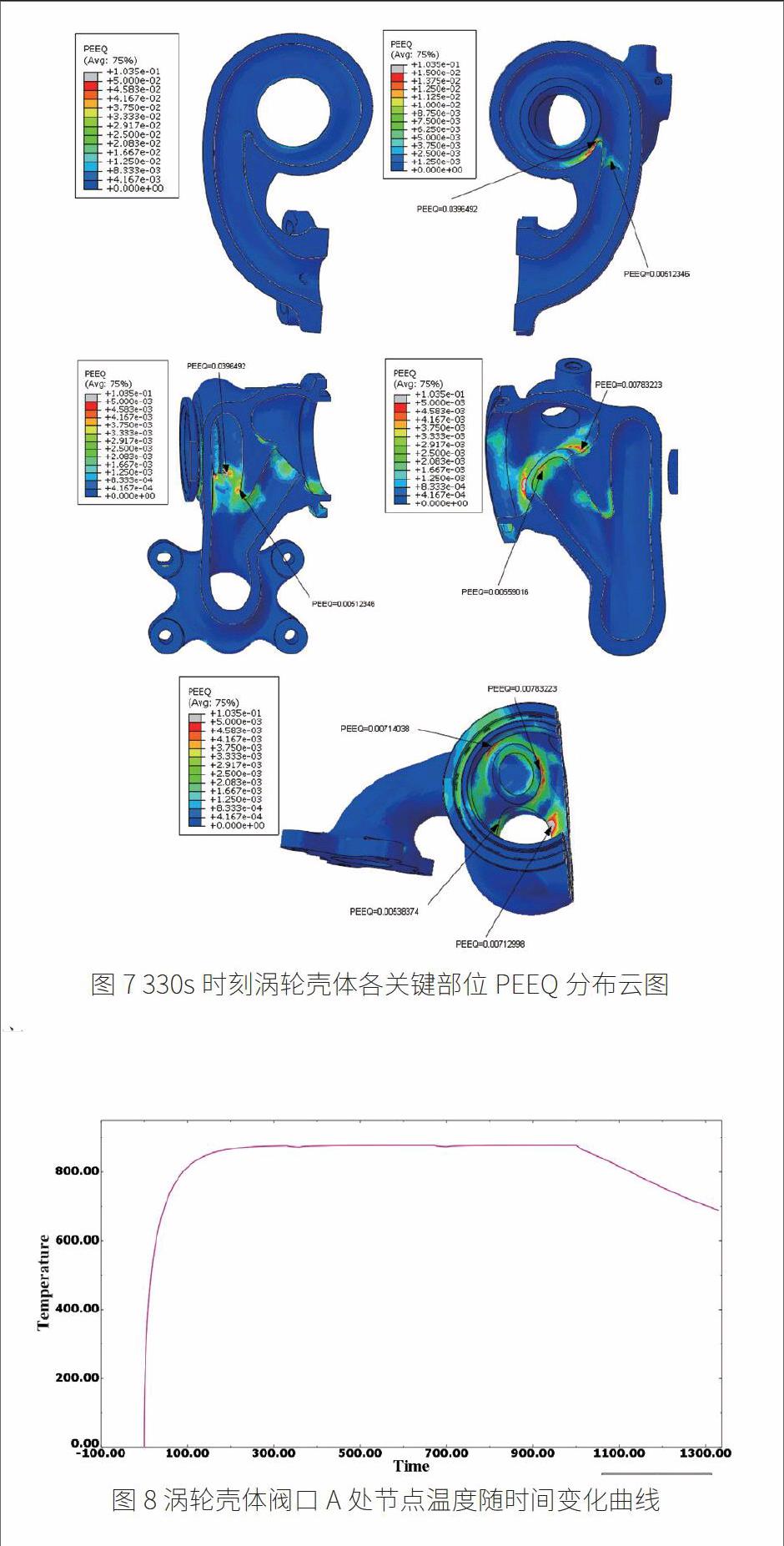
圖7所示為一個工作循環結束（330s時刻）渦輪殼體各關鍵部位等效塑性應變（PEEQ）分布云圖，由圖7可知：對所關心各區域，殼體最大PEEQ值為0.0396492，其他部位均比此值小很多，故后續以此處參數進行進一步的熱疲勞強度討論。

圖8所示為渦輪殼體閥口A處節點溫度隨時間變化曲線，由于渦輪殼體內流過的流體溫度隨發動機曲軸轉角的變化而周期性變化；在第一循環中，發動機是從冷機狀態啟動，所以渦輪殼體的溫度也相對較低，且溫度梯度很大；而從第二循環開始，發動機則是從熱機開始循環，溫度變化趨于穩定，第二循環中的最高溫度與最低溫度與第三循環已經非常接近，因此可以認為發動機的工作溫度變化處于準穩定狀態。所以，在仿真分析中，若考慮計算時間的經濟性，可以將第二循環的溫度結果作為結構分析的輸入溫度進行間接耦合熱應力分析，一定程度上節省了結構分析的仿真時間。

2.不同時刻等效塑性應變分析

渦輪殼體的破壞主要是由于在交變溫度和交變應力的耦合作用下，不斷累積的塑性變形導致裂紋萌生、擴展而致。在循環過程中，殼體的塑性變形情況是不斷變化的，比如，某些區域在升溫過程中是拉應力，而在降溫的過程中是壓應力，兩種應力狀態雖對塑性變形的貢獻不一樣，但都會引起裂紋的擴展。因此，本文采用等效塑性應變PEEQ來作為是否會發生裂紋擴展的指標，其物理定義為整個過程中塑性變形的累積。

圖9所示依次為330s、660s和990s時刻部件最大等效塑性應變值，由圖9可知：最大等效塑性應變依次為0.0396492、0.0399607和0.040064，即該處的塑性應變主要發生在第一個循環過程，在第二第三個循環中，塑性應變變化較少且趨于穩定，三個循環過后的PEEQ為0.040064，循環3產生的PEEQ為0.0001033，數值較小，可認為后續循環造成疲勞破壞的危險很小；故對渦輪殼體熱疲勞分析時，將第一次循環后等效塑性應變與靜拉伸時結構的真實斷裂應變進行比對，即可初步判定結構的熱疲勞特性。

五、結語

本文采用Abaqus對渦輪增壓器殼體進行瞬態熱應力分析，通過分析得出以下結論。

（1）仿真獲得的渦輪殼體瞬態溫度場在第二個工作循環后趨于穩定，對后續快速計算渦輪殼體結構分析提供了方向和指導方法。

（2）通過分析整個循環工況下渦輪殼體的等效塑性應變的變化過程與數值可對渦輪殼體的熱機械疲勞安全進行初步的評估與預測。endprint