一種基于指紋特征比特串和級聯編碼的生物加密方案

◆陳卓洋 方勇 謝承洋

?

一種基于指紋特征比特串和級聯編碼的生物加密方案

◆陳卓洋 方勇 謝承洋

（四川大學電子信息學院 四川 610064）

本文主要研究以指紋為對象的生物特征加密技術。生物特征加密技術是生物識別技術與密碼學的有機結合。由生物特征生成的密鑰既可以對數據直接進行加密也可以對密鑰進行加密保護，并且具有不易被盜、被遺忘，不易破解等優點。本文提出了一種基于指紋特征比特串的加密方案，首先將指紋信息轉換為比特串，再運用兩級串行級聯的糾錯編碼，保護密鑰或者秘密信息。實驗結果表明，該方案安全性較高，系統開銷較小，并且能夠保護用戶指紋特征信息，具有一定的實際應用價值。

生物加密；模板保護；糾錯編碼；級聯編碼

0 引言

傳統的口令或密碼已難以保障信息系統的安全，而基于生物特征的身份認證技術，已廣泛地應用于金融、國防、電子商務等領域。然而，隨著人們對生物特征識別技術的深入研究，逐漸發現生物特征識別技術存在一些固有的安全隱患和缺陷：由于生物特征的唯一性，一旦丟失則是永久性的丟失。這使得生物特征隱私保護成為一個重要的安全問題。

生物特征加密技術是生物特征識別技術與傳統密碼學技術的有機融合，該技術將生物特征與密碼技術用某種方式相結合，為密鑰和生物特征模板提供一種全新的安全保護措施，可有效解決上述安全問題。

1 相關研究

目前，國內外有大量的專家和機構對生物特征模板保護技術展開了研究，并在指紋、掌紋、視網膜、虹膜、靜脈、臉型、等生物特征方面取得了一定的成果。本文主要針對個人指紋特征進行研究。1994年A.Bodo首先提出將密鑰和生物特征相結合，使用生物特征保護密鑰[1]。1999年等人提出了模糊金庫（）方案[2]，其核心思想是將生物特征信息隱藏于大量的干擾信息之中，只有合法用戶才能過濾除干擾信息繼而獲得密鑰的使用權。等人在2010年提出了一種基于指紋細節點比特串的模板保護方案[3]。其基本思想是將指紋信息進行安全域轉換，提取指紋特征比特串，然后通過計算注冊模板和活體模板對應的比特串的相似度來判斷指紋是否同源。2015年茹宇[4]對的方案進行了改進，引入混沌序列，生成可撤銷模板，提高了抗交叉模板攻擊性能。唐宇[5]在的基礎上，對比特串的生成技術進行了改進，將三維投影降到二維投影，減短了二進制位數，提高了系統效率。但是此方案必須存儲原始注冊指紋二進制串信息，一旦攻擊者獲得指紋模板讀取順序，那么就可以從特征比特串恢復出原始指紋信息，從而導致用戶隱私信息泄露。之后，[6]等人在的基礎上將比特串和BCH編碼結合，提出了一種基于模糊承諾的加密方案，降低了誤識率和拒識率，同時沒有直接存儲指紋特征比特串，進一步保護了指紋模板安全。但是其方案的耗時較大，系統效率較低。針對方案存在的問題，本文提出一種改進的加密方案，運用兩級級聯的糾錯編碼方案，增加信息冗余，降低匹配用時，提高系統性能。

2 基于指紋特征比特串和級聯糾錯編碼的生物加密方案

2.1 指紋信息安全域轉換

指紋信息在實際中信息量是無限大的，而且直接儲存指紋圖像信息極易造成丟失風險。因此，對于指紋信息首先通過不可逆變換，要將其轉換到安全域進行處理。本文運用唐宇[5]提出的改進的指紋比特串生成方案，將生成的特征向量投影到二維矩陣空間，量化讀取矩陣空間數值，生成比特串，組成比特串矩陣，實現指紋信息的安全域轉換。實現方案如下：首先利用模式識別已有圖像技術進行預處理[7]，提取指紋原始細節點，計算每兩點之間的相對特征向量，用以表示其在指紋圖像中的相對位置，然后建立二維空間矩陣，將其投影到矩陣中，并量化標記此矩陣，之后以可變的順序遍歷它，生成一個細節點對應的特征比特串，最后將每個細節點的特征比特串組合在一起組成指紋特征比特串矩陣。

2.2 模糊承諾思想

生物特征具有模糊性，也可以看作具有噪聲的隨機信號，即使是同一個生物特征再次提取時，最多能獲得與注冊生物模板時比較接近但不完全相同的特征信息，但是對于傳統密碼技術而言，用作加解密的密鑰數據必須是完全一致的。為了解決這個難題，[8]等人將糾錯編碼技術和傳統加密技術想結合提出了模糊承諾算法，其基本思想是：用散列函數隱藏原始碼字，但是公開偏差，用來向證據提供具有彈性的輔助信息以便能夠解開承諾。模糊承諾算法包括承諾與解承諾兩個階段。在承諾階段用證據來承諾碼字，其中和的長度均為，證據可以用和偏差來唯一表示，承諾包含{，}，其中為承諾碼字的散列函數值。在解承諾階段，用戶輸入證據，然后計算，如果與足夠相似，進一步可以通過計算與的散列函數值是否相等來驗證解承諾是否成功。算法示意框圖如圖1所示。

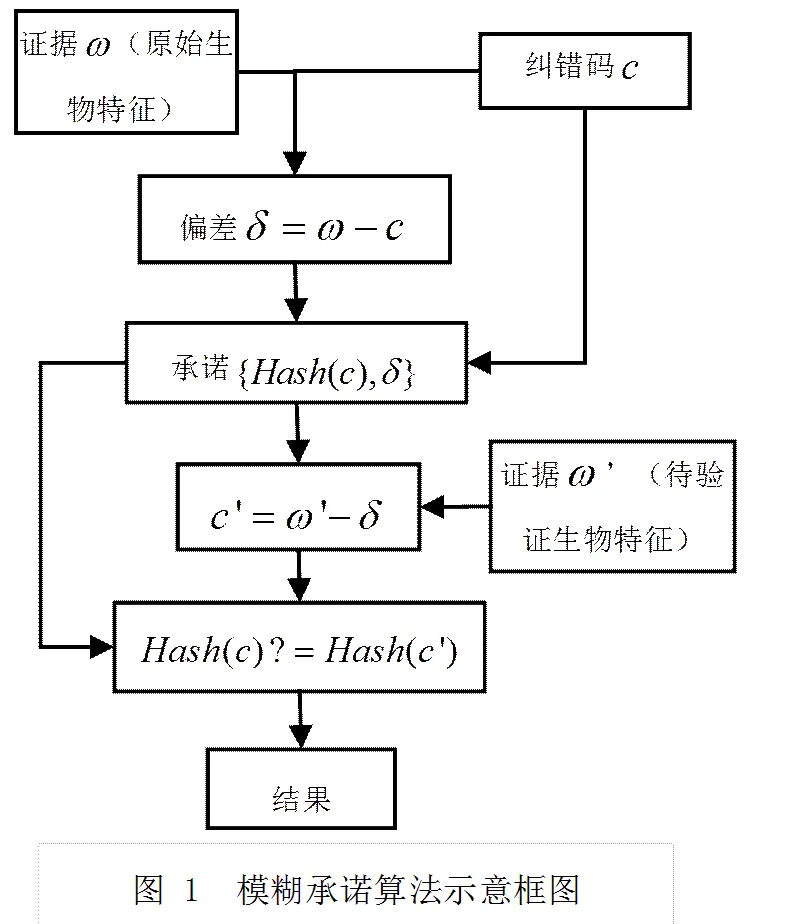
在模糊承諾方案中糾錯編碼技術起著至關重要的作用，正是因為糾錯編碼的使用才能克服生物加密系統中生物特征具有的模糊性和隨機性。在的方案中，采用了編碼技術。本方案對其進行改進，采用碼和卷積碼兩級級聯的方案。這樣的優勢在于：一是因為兩級譯碼處理較之同等長度的單級譯碼而言，復雜度要小得多[12]。二是兩級級聯方案能產生較大信息冗余，從而提高信息的安全性。三是碼適合糾隨機錯誤，而采用級聯方案，可以選取不同糾錯編碼來實現既能糾隨機錯誤，也能糾突發錯誤。

碼是一種特殊的非二進制碼，它定義在伽羅華域2上，其中每個符號由位比特組成。由于碼是以符號為單位實現對差錯的控制的，因此特別適合于糾正突發錯誤。記碼為nk，其中k表示編碼前的符號數，n表示編碼后的符號數，表示該碼可以糾正的錯誤個數，各參數滿足如下約束關系：n-k=2。

卷積碼是一種非分組碼，其主要特點是編碼器是有記憶的，因此適合糾正隨機錯誤。記卷積碼為nk，其中k表示編碼前的比特數，n表示編碼后的比特數，表示存儲器的個數。編碼器在任意時刻的n個輸出不僅與該時刻的k個輸入有關，還與該時刻個存儲器中的狀態（即前個時刻的輸入）有關。

2.3 方案實現

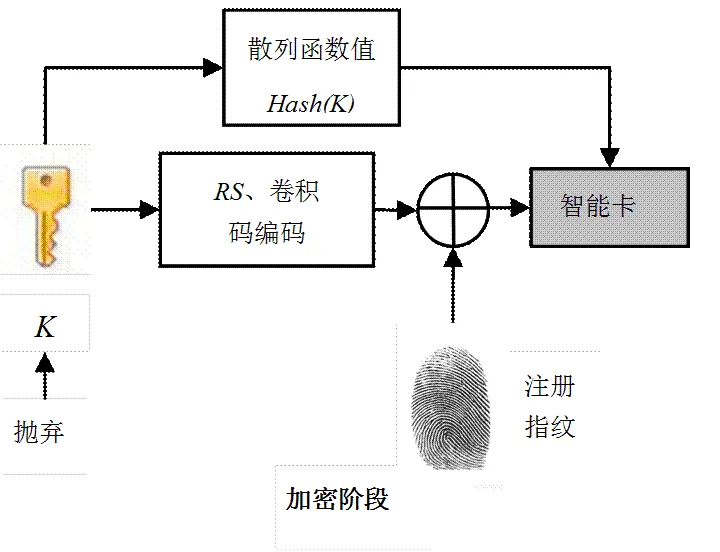
方案的基本思路是，首先從原始指紋圖像中提取出固定的長度為的特征比特串，然后采用模糊承諾算法思想，首先隨機產生一個，經過糾錯編碼后產生一個長度為的密鑰，并與長度同樣為的指紋特征比特串進行異或操作，所得的結果存儲為生物特征模板，并拋棄原始的。在解密時如果用于比對的指紋和原始指紋來自同一個人，那么解密成功，恢復出。方案總體流程如圖2所示。

加密階段，將一個隨機生成的二進制密鑰編碼為與指紋特征比特串長度相同的二進制序列，之后將此編碼后的二進制隨機序列與特征比特串矩陣相異或，生成生物密鑰K。此過程具有單向性，即由生物密鑰K無法導出隨機密鑰或原始指紋信息。

解密階段，則首先從用戶的指紋中提取指紋細節點特征比特串矩陣H′，再用此特征比特串矩陣和存儲的K異或，異或的結果再解編碼，若解碼成功且通過哈希值驗證后恢復得到密鑰′。

下文將詳細說明具體細節。

2.3.1 加密階段

（1）從用戶注冊指紋中提取指紋特征比特串，長度為。系統隨機生成二進制密鑰，之后采用編碼算法，將進行一次編碼，然后用卷積碼進行二次編碼，編為長度同樣為的二進制序列K。計算密鑰的散列函數值（），并將拋棄。

（2）將編碼后的二進制序列K與指紋特征比特串矩陣H中的每一個特征比特串β相異或，得到得到個二進制序列并組成加鎖矩陣K，并將其存儲在智能卡中。

2.3.2 解密階段

（1）從系統數據庫中提取矩陣K。采集待驗指紋，提取指紋特征比特串，得到由個特征比特串b組成的特征比特串矩陣H′。

（2）依次從特征比特串矩陣中取出第個比特串，并與系統數據庫中的K進行異或。得到個二進制序列K。

（3）用卷積碼和RS碼解碼算法對個二進制序列K進行糾錯解碼，若解碼成功則恢復出密鑰，否則，回到（2）繼續從b中取出下一個比特串，直到遍歷完所有的b，若仍無法成功，則密鑰生成失敗并結束。

（4）計算密鑰的散列函數值（），判斷（）是否等于（），若相等則說明=并輸出密鑰作為最終密鑰。否則，密鑰生成失敗并結束。

3 實驗測試與性能分析

本文采用2012編程環境，采用公開指紋庫。同時，由于公開庫質量較差，我們實際采集了80個指紋，作為實際采集指紋庫進行對比。

3.1 實驗參數選取

本文采用的糾錯編碼算法中，需要確定兩級糾錯編碼，即nk和nk的參數。卷積碼的編碼參數，我們根據文獻給出的最優卷積碼，即（4，1，6）卷積碼。碼采用定義在（2）上的編碼，即=1。由此可得，隨機密鑰的長度由公式（1）確定。

k=k×m-v （1）

由編碼特性，k=n/m-2t，得出隨機密鑰和編碼后的長度，碼的容錯位數之間的關系如公式（2）。

2）

由此可知，需要確定三個參數。只需確定其中兩個參數，就可確定第三個參數。

3.1.1 參數n的選取

編碼后碼元的長度等于特征比特串的長度而特征比特串長度取決于二維空間矩陣的長寬和矩陣單元的長寬。參數的數值選取應盡量使同源指紋對應比特串之間的相似度較高，而不同源的指紋特征比特串較低。特征比特串的相似度可以由公式（3）計算。

實驗中，分別采用公開指紋庫和實際采集指紋庫中的80幅指紋圖像進行測試，這80幅指紋圖像采集于8個不同的手指，每個手指采集10次。將每個指紋圖像進行特征比特串提取操作，然后計算同源指紋（即真匹配）和不同源指紋（即假匹配）特征比特串的平均相似度。表1列舉了指紋庫的和實際采集指紋測試結果。

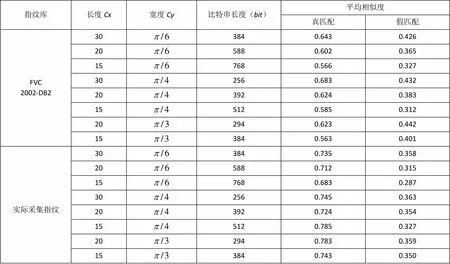
表1 不同配置參數下的真假匹配情況

綜合真假匹配平均相似度以及比特串長度，對于指紋庫和實際采集指紋庫都選取特征比特串長度=512作為最優參數，即編碼長度==512。

3.1.2 參數t的選取

參數的選擇應使合法用戶提供的特征比特串通過糾錯后能夠與模板比特串一致，而非法用戶提供的特征比特串在容錯能力下無法完成糾錯，進而無法恢復出正確密鑰。

實驗采用從指紋庫中的80幅指紋圖像對生成的特征比特串進行實驗分析，分別計算同源指紋對應比特串、同源非對應比特串及非同源指紋比特串的錯誤位數，并分別記錄其中2000次的比對結果。如圖3所示。從實驗結果發現同源指紋的對應比特串的錯誤位數與非同源指紋比特串及同源非對應比特串錯誤位數之間的具有明顯的區分度，可以選取一個恰當的閾值作為容錯位數t的取值范圍。

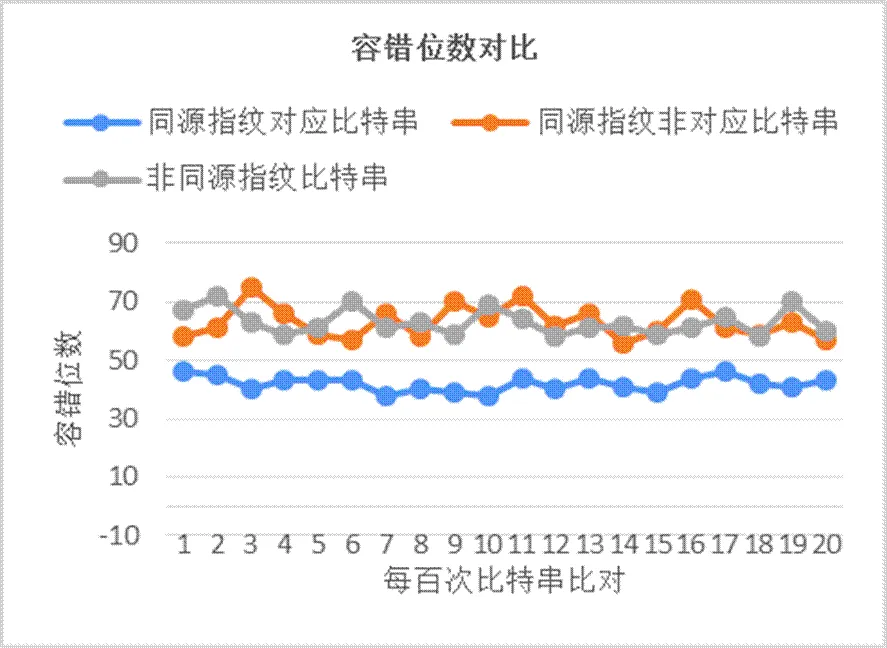
圖 3 指紋特征比特串容錯位數對比示意圖

經過實驗得出同源指紋對應比特串之間的平均錯誤位數為約為42位，而非同源指紋比特串的平均容錯位數為62位，閾值可以設置在42位到62位之間，即42<4<62。此外，從理論上講，的取值會對拒識率（）和誤識率（）造成影響。在一定范圍內，若的取值越大拒識率會降低，誤識率會增大，相反，若的取值越小拒識率會增大，誤識率會降低。在實際使用中，可以根據需求和測試需要以此值為基準，上下浮動選取的取值。

3.2 實驗結果分析

實驗分別選取指紋庫中的80幅指紋圖像和實際采集的80幅指紋圖像進行實驗測試。其中有560次為真匹配，其余為假匹配。計算在不同級聯方案下的拒識率（）和誤識率（），結果如表2所示。方案的曲線如圖4所示。

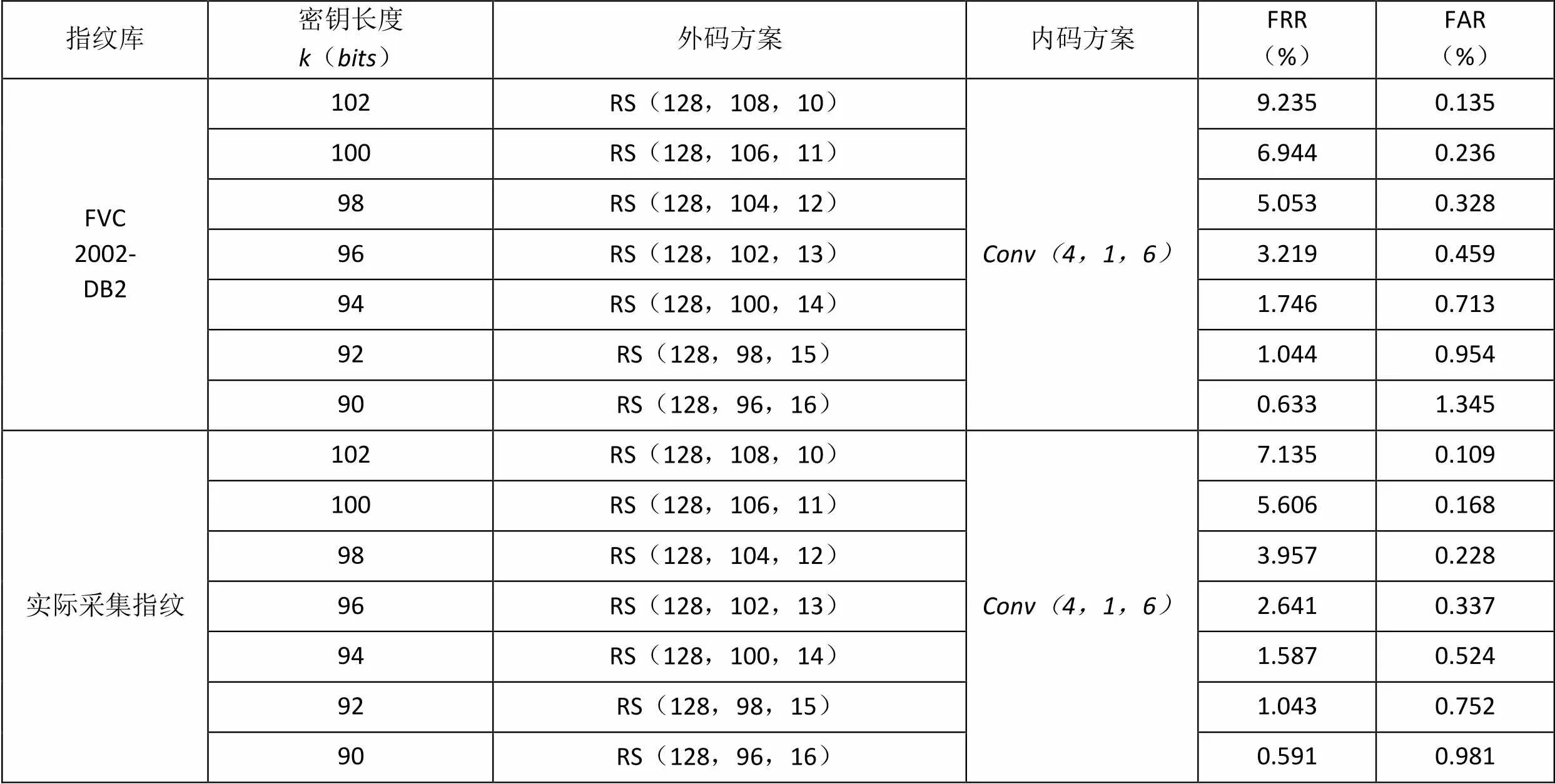
表2 不同級聯方案下的拒識率和誤識率

從表2顯示的實驗結果可以看出，該方案的拒識率（）和誤識率（）可以獲得比較理想的測試結果。同時隨著容錯位數的增大，拒識率（）會降低，但誤識率（）會升高。而且由于實際采集指紋質量較好，測試結果也優于。在實際運用中，可以參考圖4所示的曲線，根據不同的應用需求與場合來選擇不同的參數，以更好的滿足主要應用目的。

本文提出方案與方案相比，鑒別性能稍有提高，但是由于級聯方案在編碼效率上比單級編碼高，譯碼耗時少[12]，時間開銷比XIE的方案降低至少20%。同時，信息冗余度方面，的方案為0.872，本方案為0.199，增加了大量冗余，安全性更高。

3.3 安全性分析

3.3.1 抗暴力破解攻擊

（1）針對指紋模板的暴力攻擊方面，本方案的整個過程中均不需要存儲原始指紋信息，而只需要存儲輔助信息，即經過與編碼后的隨機密鑰進行異或后的指紋特征比特串，而輔助信息的生成是一個不可逆的過程，無法從輔助信息獲得指紋特征信息，因此暴力破解在計算上是不可行的。而針對密鑰的暴力攻擊，本文采用（128，102，13）和（4，1，6）級聯方案，若攻擊者想直接生成編碼后的二進制序列BCH，那么他必須生成512位二進制序列，其中52位允許容錯，那么他成功的概率為2-460。

（2）若攻擊者想直接生成密鑰，那么正確的概率為2-96。

（3）若攻擊想生成用散列函數加密之后的密鑰，則安全性取決于散列函數的安全性，散列函數加密后的密鑰長度通常為128或256位，則成功的概率為2-128或2-256。

3.3.2 抗多模板交叉匹配攻擊

在指紋特征模板安全域轉換過程中，提取到的指紋比特串由單元矩陣的取值和訪問量化標記后的二維矩陣的順序這兩個參數決定，而這兩個參數決定了提取的比特串的長度，這樣一來采用長度為的比特串提取方案，就有！個順序可供選擇。因此，在實際系統中，只要通過設置不同的參數，即可以使從同源指紋中提取的兩個比特串完全不同，無法進行匹配，從而可以抵抗同源指紋的多模板交叉匹配攻擊。

4 結束語

本文研究了指紋信息的安全域轉換，然后對基于糾錯編碼的加密方案提出了改進方案，采用級聯編碼代替單級編碼，在提高安全性的同時降低了系統開銷，具有一定的實際應用價值。指紋信息和密碼學的有機結合，必將為指紋識別技術帶來更加廣闊的應用前景。

[1]A.Bodo.；Method for Producing a Digital Signature with AidofaBiometricFeature [P]. GermanPatent：DE42-43-908-A1，1994.

[2]Juels A.，Sudan M.；A Fuzzy Vault scheme[C]. Proc of International Symposium on Information Theory [S.l.]：IEEE Press，2002.

[3]Chulhan Lee，Jaihie Kim，Cancelable fingerprint templates using minutiae-based bit-strings [J].Journal of Network and Computer Applications，2010.

[4]茹宇.基于混沌序列的指紋特征模板保護技術研究[D].成都：四川大學，2015.

[5]唐宇.基于指紋比特串的生物特征加密技術研究與應用[D].成都：四川大學，2015.

[6]Cheng-Yang XIE，Jia-Yong LIU，Xu YAO，Dian-Hua TANGA. Research of Biometric Key Generation Based on Fingerprint Bit-strings.Journal of Fiber Bioengineering and Informatics，2015.

[7]李昊，傅曦.Visual C++指紋模式識別系統算法與實現[M].人民郵電出版社，2008.

[8]Juel A，and Wattenberg M. A fuzzy commitment scheme[C]. Proc. Of the 6th ACM Conf. Computer and Comm. Security（CCCS），1999.

[9]Andre Neubauer，Jurgen Freudenberger，Volker Kuhn（作），張宗橙（譯）.Coding theory：algorithms，architectures and applications[M].人民郵電出版社，2009.