基于遺傳算法帶約束的翼傘系統歸航軌跡設計

陶金，孫青林，朱二琳，陳增強，賀應平

?

基于遺傳算法帶約束的翼傘系統歸航軌跡設計

陶金1，孫青林1，朱二琳1，陳增強1，賀應平2

(1. 南開大學計算機與控制工程學院，天津，300350；2. 中航工業宇航救生裝備有限公司，湖北襄陽，441003)

翼傘系統歸航軌跡設計是一類帶約束的最優控制問題，引入一種具有精英策略的遺傳算法解決此類問題。為方便使用遺傳算法，引入非均勻B樣條曲線擬合控制律，將最優控制問題轉化為B樣條基函數控制頂點的參數優化問題，并針對歸航終端等式約束，引入松弛因子將其轉化為不等式約束，進而采用靜態罰函數法處理。在2種不同初始條件下的歸一化模型中進行仿真，并針對實際工程中著陸精度要求設定3種不同的松弛因子。仿真結果表明：使用本文的方法解算出的歸航軌跡及其控制信息合理，是符合工程實際需求的一種有效方法。

翼傘系統；歸航軌跡優化；遺傳算法；罰函數；約束處理；松弛因子

翼傘系統[1]歸航軌跡設計是指給定起始點和目標點，在特定的動力學約束基礎上，規劃1條滿足特定性能指標的最優路徑。傳統的最優歸航軌跡設計方法是基于控制論的優化算法，主要分為間接法和直接法。間接法是通過由變分法或龐特里亞金極大值原理得到的最優條件來求解最優歸航軌跡。比較有代表性的研究成果有熊菁[2]運用極小值原理將歸航軌跡規劃的最優控制問題轉化為兩點邊值問題，然后采用共軛梯度法進行求解；SLEGERS等[3]將翼傘系統歸航中最后階段(逆風對準) 的最優控制問題轉化成兩點邊值問題求解。由于間接法求解過程比較繁瑣，因此，在進行翼傘系統歸航軌跡設計時，多采用直接方法求解。直接法是把含有性能指標的最優控制問題轉化為非線性規劃問題進行歸航軌跡設計。比較有代表性的研究成果有ZHANG等[4?5]使用高斯偽譜法將翼傘系統歸航軌跡離散處理轉化為具有一系列代數約束的大規模非線性優化問題，并用二次規劃方法進行求解；CLEMINSON等[6]采用動態規劃法對翼傘系統自動歸航路徑進行了研究。但無論是間接法還是直接法，由于都是采用傳統的基于梯度的搜索方法，因此，對初值十分敏感，優化結果在很大程度上取決于對初始值的猜測，因而限制了其在工程上的應用。近年來，隨著計算機技術的發展，涌現出大批新型的智能進化算法。這些算法具有較強的魯棒性和廣泛的適應性，對初始值不敏感，以高效、實用的特點吸引著學者嘗試用于解決翼傘系統歸航軌跡設計問題。比較有代表性的研究成果有LIU等[7?8]采用改進的粒子群算法尋優得到了基于最優控制的翼傘系統歸航軌跡的近似最優解；焦亮等[9]使用混沌粒子群算法對災難環境下翼傘空投機器人系統軌跡進行了規劃。以上工作對于問題的求解多是將翼傘系統歸航軌跡設計問題視為一類多目標優化問題，使用權重因子的方法將多目標優化轉化為單目標優化，然后進行單目標函數尋優，優化結果嚴重依賴于權重因子的選擇。其他關于翼傘系統軌跡規劃的研究成果有：ROSICH等[10]對翼傘系統的群體歸航的軌跡及控制規則進行了研究；LUDERS等[11]提出了一種基于快速擴展隨機樹的在線規劃算法，在任意非凸的繪制地圖上實現了翼傘系統風擾下精確歸航的無碰路徑生成；LEE等[12]提出了1種兩點邊值貝葉斯曲線軌跡規劃方案；JONATHAN等[13]針對翼傘系統歸航過程中易受風影響的問題提出了1種選擇性軌跡規劃方式來確定所跟蹤的預定軌跡。與上述的大部分研究工作不同的是，本文作者將翼傘系統歸航軌跡設計問題歸納為一類具有約束的最優控制問題，采用1種具有精英策略的遺傳算法進行歸航軌跡尋優，解決傳統方法初始值難以估計的問題；將著陸距離偏差和逆風對準兩項歸航指標視為控制約束，對單一能耗目標函數進行優化，且引入帶松弛因子的靜態罰函數法處理約束，松弛因子可以根據不同工程實際需求進行設定，減少了加權因子選擇的困難，也使規劃結果可控，且更加符合工程實際需求。

1 最優控制問題描述

翼傘系統歸航軌跡設計問題的本質是一類非線性，帶有狀態約束、控制約束和終端約束的最優控制問題，從以下4個方面進行闡述。

1.1 系統數學模型

翼傘系統動力學模型復雜，非線性強，耦合多，因此，在翼傘系統歸航軌跡規劃中通常采用相對簡單的質點模型，以簡化計算。本文通過對文獻[14]中的全展開翼傘系統六自由度運動模型進行仿真，并進行一定的假設簡化，提煉出翼傘系統質點模型的運動方程，用來代替復雜的高自由度模型進行歸航軌跡的最優設計。

翼傘系統質點模型歸航軌跡設計通常采用風坐標系，風坐標系中各坐標軸的方向與大地坐標系一致，但其坐標原點隨著氣流而運動。這樣可以將風的大小、方向以及系統隨高度的變化等影響都轉化到起始點的位置偏移中。由于翼傘系統的飛行控制是通過左右電機帶動絞盤上纏繞的翼傘后緣兩側的操縱繩來實現的，無論是單側下偏操作還是雙側下偏操作，當下偏量在能夠維持翼傘系統穩定飛行范圍內波動時，其水平飛行速度和滑翔比變化很小，因此，進行以下假設，用來簡化模型：

1) 在翼傘充滿后完全展開的穩定飛行狀態下，忽略大氣密度變化和左右下偏操作對翼傘系統飛行速度的影響，認為其水平飛行速度和滑翔比保持不變。

2) 只考慮水平風場，且風向和風速是已知的，忽略風對翼傘系統姿態的影響。

3) 系統對控制輸入的響應無延遲。

基于以上3點假設，在風坐標系之上，選取目標點(設定為翼傘系統開始實施雀降著陸時的坐標點)為坐標原點，翼傘系統的運動方程可以簡化為

其中：，和分別為翼傘系統在風坐標系軸、軸和軸的坐標信息；S為翼傘系統水平飛行速度；v為垂直下落速度；為偏航角；為偏航角速率；為控制量；與偏航角速率(即翼傘系統操縱繩的單側下偏量)存在一一對應的關系。

1.2 邊界條件與目標集

基于上述的假設條件和質點模型，在翼傘系統歸航軌跡設計問題中，初始時刻、初始狀態及末端時刻、末端狀態都是已知和固定的。將邊界條件和目標集概括如下。

1.2.1 初始狀態

翼傘系統歸航的初始時間為0，則其初始條件可以表述為

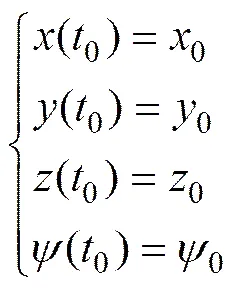
式中：0，0和0為起始時刻翼傘系統坐標信息；0為起始時刻偏航角。

1.2.2 終端約束

翼傘系統歸航的終止時間為f，則f=0/v，終端狀態可以表述為

式中：f，f和f為著陸點坐標信息，wind為水平風向，著陸方向wind(f)與wind的偏差為±(2+1)π，是為保證翼傘系統著陸時刻逆風。

1.3 容許控制

容許控制表示如下：

式中：為控制域，其取值范圍為[?max，max]，max為允許輸入的最大控制量，與翼傘系統最小轉彎半徑相對應。

1.4 性能指標

翼傘系統歸航所需滿足的條件可以歸納如下。

1) 著陸點距離目標點近。

2) 逆風著陸。這是翼傘系統實施雀降的必要條件，通過雀降可以減小翼傘系統著陸時的速度，避免著陸過程中對回收物造成損傷。

3) 能耗少。這要求歸航控制過程中電機消耗的能量越少越好。

根據翼傘系統歸航所需滿足的條件，選取條件(3)最小能量消耗作為最優控制問題性能指標：

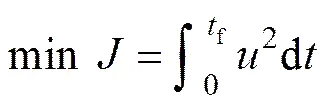
條件1)和2)則視為翼傘系統歸航最優控制問題約束條件，表示為

(6)

式中：約束條件1()=0表示終端時刻著陸點與目標點偏差為0，即在目標點著陸；2()=0表示著陸時刻航向角(f)與風向wind偏差為±(2+1)π，即逆風著陸。

根據上述翼傘系統歸航最優控制問題基本組成部分，歸納一般提法為：在滿足系統運動方程(1)的約束條件下，在容許控制域(4)中確定1個最優控制律*，使系統狀態從初始狀態(2)轉移到要求的目標集合(3)，滿足約束條件(6)，并使性能指標(5)達到最優。這是一類典型Lagrange型最優控制問題，進一步描述為翼傘系統歸航過程中用較少的能耗使得終端時刻著陸點與目標點偏差在要求范圍內且符合逆風著陸條件。其等效的優化問題模型為

2 基于遺傳算法的歸航軌跡設計

針對所述的帶有約束的最優控制問題，采用類具有精英策略的遺傳算法進行解算。首先將各變量歸一化處理以提高求解問題的精度；引入非均勻B樣條技術進行控制律的擬合以實現參數化；約束條件采用帶松弛因子的靜態罰函數法進行處理。

2.1 歸一化處理

在翼傘系統歸航軌跡優化過程中，由于狀態變量的量級相差較大，在軌跡積分的過程中會導致有效位數的損失，歸一化處理可以有效克服這一問題，提高計算精度。另外，對歸航軌跡的優化也要求優化變量盡可能地保持在相同的量級，故作以下處理，令

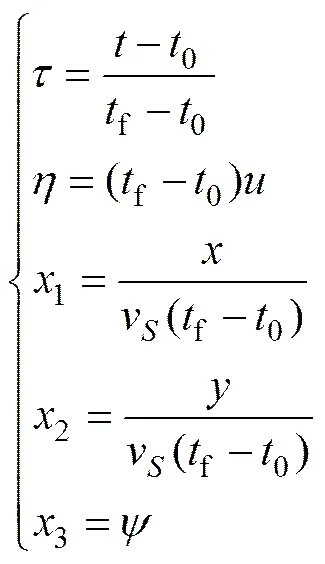
則運動方程式(1)轉化為

(9)

初始狀態式(2)轉化為

終端約束式(3)轉化為

(11)

容許控制式(4)轉化為

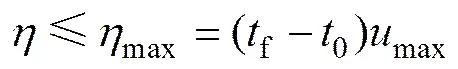
約束條件式(6)轉化為

(13)

等效的優化問題描述式(7)轉化為

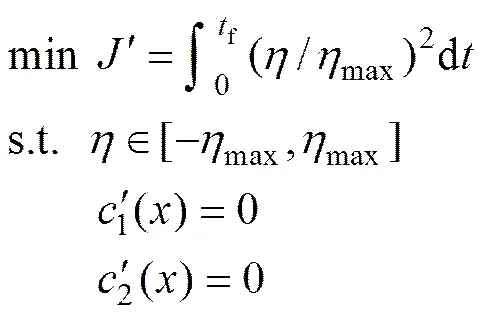
2.2 參數化方法

翼傘系統歸航軌跡的優化空間是泛函空間，使用遺傳算法不能直接進行解算，因此首先要將最優控制問題轉化為參數優化問題。常用的參數化方法主要有直接離散法、多重參數插值法和函數逼近法。本文為簡化編碼及計算的復雜度，考慮到翼傘系統控制量必須是連續的，采用非均勻B樣條技術[9,15]逼近控制率的方法來實現參數化。非均勻B樣條擬合曲線定義如下：

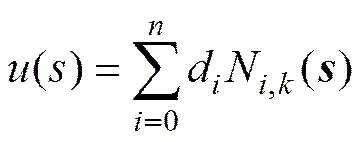
式中：d為第個控制頂點；N,k()為由節點矢量= [0，1，…，s+k+1]決定的次B樣條基函數；=0，1，…，，本文中采用德布爾?考克斯遞推方法得到。次B樣條基函數的支撐區間為[s，s+k+1]，包含+1個節點區間，節點矢量可采用哈特利?賈德公式來確定。按照上述方法對控制變量進行編碼。根據式(15)，給出若干控制定點d，為控制頂點的個數。一般來講，控制點個數越多，所描述的控制規律越精確，但無疑又會增加相應計算量，本文中選用7個控制頂點，基函數選取常用的3次非均勻B樣條曲線。

2.3 約束條件處理

使用遺傳算法對問題目標進行優化必須對約束條件進行處理，但目前來講，還沒有處理約束的一般性方法，通常的處理方法有搜索空間限定法、可行解變換法和罰函數法。對于軌跡優化問題，罰函數法是一種有效方法。本文中引入松弛因子將終端等式約束轉化為不等式約束，進而采用一種簡單的靜態罰函數法進行處理。引入松弛因子1和2，約束條件式(13)可化為

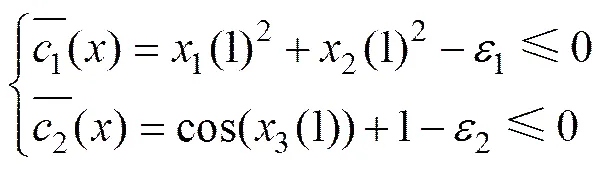
(17)

式中：1和2為懲罰函數系數，其值的選取要度量解對約束條件的不滿足程度和計算效率，用以調整懲罰函數懲罰度，本文選取1=1，2=0.3。由上述可知：當滿足約束條件時，；當不滿足約束條件時時，，增加相應懲罰，使得解個體向著滿足約束的方向進化。

2.4 遺傳算法設計

文章的結尾也很重要，既不能有頭無尾，又不能虎頭蛇尾，或畫蛇添足。初中語文教材課文中的結尾有以下幾種常用的，可供我們寫作時借鑒。

本文采用一種具有精英策略的遺傳算法解決這類帶約束的翼傘系統歸航軌跡設計的最優控制問 題[16?19]。與傳統的遺傳算法不同，本算法中引入交叉后代比例的概念，表示子代中由交叉產生的個體父代中非精英個體數的比例，其值是1個0~1的數。所采用的精英策略是指父代中的精英個體原封不動地直接傳給子代，而不經過交叉和變異操作。采用精英策略的優勢在于：在進化過程中，種群中的最優個體不會因為選擇、交叉和變異操作而破壞或丟失，對改善遺傳算法的收斂性有重要作用。RUDOLPH[19]使用有限齊次馬爾科夫鏈證明了僅采用選擇、交叉和變異的經典遺傳算法無法收斂到全局最優，而具有精英策略的遺傳算法是全局收斂的。本文中精英策略的具體操作為將保留的精英個體直接替換子代中適應度最低的相同數目的個體，從而保證種群規模的一致性。

本文中采用實數編碼，編碼方法采用非均勻B樣條技術，B樣條基函數的控制頂點即組成了遺傳空間染色體上的基因。種群規模取為100，精英個體數目取為20，迭代次數取為200，交叉后代比例取為0.75.

3 仿真算例與分析

3.1 仿真條件

作為仿真實例，本文選用空投質量w=80 kg的傘型，翼傘展弦比=1.73，傘繩長度l=3.7 m，吊帶長度w=0.5 m，傘衣面積p=22 m2，空頭物阻力特征面積w=0.5 m2，安裝角=7°。根據所選的傘型及其六自由度仿真結果，在保證翼傘系統傾斜角小于20°的前提下，翼傘系統基本運動參數為：初始速度s=15 m/s，v=5 m/s，電機控制量max=30，翼傘系統空投初始高度=2 000 m。

3.2 仿真結果及分析

為了全面分析翼傘系統歸航軌跡的形態、控制特點以及松弛因子選擇對歸航軌跡規劃結果的影響，以下取2種初始運動狀態，分別為初始狀態：1(0)=0.5，2(0)=0，3(0)=?π/3；初始狀態：1(0)=0.6，2(0)=0.6，3(0)=π；其對應風坐標系下實際坐標位置分別為初始狀態：0=3 000 m，0=0 m，0=60°；初始狀態：0=3 600 m，0=3 600 m，0=180°。考慮到3種工程實際翼傘系統歸航著陸精度設計要求，設定3種松弛因子方案，如表1所示。比如方案2歸航著陸精度要求為著陸點距離目標點偏差在6 m之內，著陸點方向與水平風向夾角大于等于172°。根據式(8)和(16)進行推算，松弛因子1和2可設置為：

采用本文提及的方法，分別在初始狀態和下，采用3種松弛因子設定方案進行翼傘系統歸航軌跡最優設計，并在Matlab上進行仿真分析。

表1 3種松弛因子設定方案

圖1所示為帶精英策略的遺傳算法的最優適應度值迭代曲線。從圖1可以看出：在精英策略的作用下，算法表現出良好的收斂性能，在第8代附近已基本接近最優值，獲得最優解的平均CPU時間小于2 s，符合翼傘系統實際工程控制需求。圖2所示為翼傘系統在初始狀態下，采用3種松弛因子設定方案的歸航軌跡及其對應控制曲線。圖3所示為翼傘系統在初始狀態下，采用3種松弛因子設定方案的歸航軌跡及其對應控制曲線。

1—平均適應度；2—最優適應度。

(a) X?Y平面歸航軌跡；(b) 控制曲線

(a) X?Y平面歸航軌跡；(b)控制曲線

表2給出的是翼傘系統在初始狀態和下分別采用3種松弛因子設定方案的最終歸航結果。從表2可以看出：雖然初始狀態距離目標點比初始狀態要遠，但是在相同松弛因子設定方案下，初始狀態歸航所需能耗要低于初始狀態。這是由于翼傘系統在初始狀態歸航過程中較多的采用滑翔飛行，能量消耗相對較少。

從表2可知：在松弛因子較大即條件約束較寬松的情況下，如初始條件和下方案2和3的著陸距離偏差、著陸方向偏差以及方案1的方向偏差，最終規劃結果完全符合并優于表1中所述設計要求。當松弛因子較小即約束嚴格的情況下，如方案1的距離偏差，結果雖然不能完全滿足工程實際設計要求，但仍然在可接受的范圍內。通過比較相同初始條件不同松弛因子設定方案下歸航能耗，可以得出隨著歸航精度要求降低，即松弛因子1增大，能耗也相應減小，說明遺傳算法在寬松約束條件下能夠搜索出具有更為優秀性能指標的解。

表2 歸航結果

4 結論

1) 將各變量進行歸一化處理，提高了求解問題的精度。

2) 采用非均勻B樣條曲線擬合控制律，簡化了編碼，提高了控制律的表達能力，從而將動態最優控制問題轉化成靜態參數優化問題。

3) 針對終端等式約束，引入松弛因子將其轉化為不等式約束，并采用靜態罰函數法進行處理，且松弛因子可根據工程實際著陸點精度要求進行設定。

4) 引入一種具有精英策略的遺傳算法解決此類問題，優化結果對初始值不敏感，具有較強的魯棒性。

5) 提出的方法解算出的歸航軌跡及其控制信息合理，規劃結果可控，工程人員可針對不同工程實際歸航精度設計要求設定松弛因子，以取得符合設計要求的翼傘系統歸航控制律信息。該方法為解決翼傘系統歸航軌跡優化的問題探索出了一條新路徑。

[1] 李春, 呂智慧, 黃偉, 等. 精確定點歸航翼傘控制系統的研究[J]. 中南大學學報(自然科學版), 2012, 43(4): 1331?1335.LI Chun, Lü Zhihui, HUANG Wei, et al. Guidance navigation & control system for precision fix-point homing parafoil[J]. Journal of Central South University(Science and Technology), 2012, 43(4): 1331?1335.

[2] 熊菁. 翼傘系統動力學與歸航方案研究[D]. 長沙: 國防科技大學, 2005: 72?85.XIONG Jing. Research on the dynamics and homing project of parafoil system[D]. Changsha: National University of Defense Technology, 2005: 72?85.

[3] SLEGERS N, YAKIMENKO O. Optimal control for terminal guidance of autonomous parafoils[C]//20th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Reston, VA, USA: AIAA, 2009: 2958?2978.

[4] ZHANG Limin, GAO Haitao, CHEN Zengqiang, et al. Multi-objective global optimal parafoil homing trajectory optimization via Gauss pseudospectral method[J]. Nonlinear Dynamics, 2013, 72(1/2): 1?8.

[5] 高海濤, 張利民, 孫青林, 等. 基于偽譜法的翼傘系統歸航軌跡容錯設計[J]. 控制理論與應用, 2013, 30(6): 702?708.GAO Haitao, ZHANG Limin, SUN Qinglin, et al. Fault-tolerance design of homing trajectory for parafoil system based on pseudo-spectral method[J]. Control Theory & Applications, 2013, 30(6): 702?708.

[6] CLEMINSON J R. Path planning for guided parafoils: An alternative dynamic programming formulation[C]//Proceedings of the 22nd AIAA Aerodynamic Decelerator Systems (ADS) Conference. Daytona Beach, FL, USA: AIAA, 2013: 2013?1346.

[7] LIU Zhao, KONG Jianyi. Path planning of parafoil System based on particle swarm optimization[C]//2009 International Conference on Computational Intelligence and Natural Computing. Piscataway, NJ, USA: IEEE, 2009: 450?453.

[8] 徐劍, 周德云. 基于最優控制的翼傘路徑規劃[J]. 火力與指揮控制, 2010, 35(10): 59?61. XU Jian, ZHOU Deyun. A path planning of parafoil system based on optimal control[J]. Fire Control and Command Control, 2010, 35(10): 59?61.

[9] 焦亮, 孫青林, 亢曉峰. 基于混沌粒子群優化算法的翼傘系統軌跡規劃[J]. 復雜系統與復雜性科學, 2012, 9(1): 47?54.JIAO Liang, SUN Qinglin, KANG Xiaofeng. Route planning for parafoil system based on chaotic particle swarm optimization[J]. Complex Systems and Complexity Science, 2012, 9(1): 47?54.

[10] ROSICH A, GURFIL P. Couling in-flight trajectory planning and flocking for multiple autonomous parafoils[J]. Journal of Aerospace Engineering, 2012, 226(6): 691?720.

[11] LUDERS B, SUGEL I, HOW J P. Robust Trajectory Planning for Autonomous Parafoils under Wind Uncertainty[C]//Aemerican Institute of Aeronautics and Astronautic Conference. Reston, VA, USA: AIAA, 2013: 1?27.

[12] LEE F, JONATHAN R. Bézier curve path planning for parafoil terminal guidance[C]//Proceedings of the 22nd AIAA Aerodynamic Decelerator Systems(ADS) Conference. Reston, VA, USA: AIAA, 2013: 2013?1325.

[13] JONATHAN R, NATHAN S. Robust parafoil terminal guidance using massively parallel processing. Journal of Guidance[J]. Control and Dynamics, 2013, 36(5): 1336?1345.

[14] JIAO Liang, SUN Qinglin, KANG Xiaofeng, et al. Autonomous Homing of Parafoil and Payload System Based on ADRC[J]. Journal of Control Engineering and Applied Informatics, 2011, 13(3): 25?31.

[15] BELAIDI H, HENTOUT A, BOUZOUIA B, et al. NURBS trajectory generation and following by an autonomous mobile robot navigating in 3D environment[C]//2014 IEEE 4th Annual International Conference on Cyber Technology in Automation, Control, and Intelligent Systems (CYBER). Pisctaway, NJ, USA: IEEE, 2014: 168?173.

[16] 劉揚, 魯乃唯, 殷新鋒. 基于體系可靠度的鋼桁梁結構優化設計[J]. 中南大學學報(自然科學版), 2014, 45(10): 3629?3636.LIU Yang, LU Naiwei, YIN Xinfeng. Structural optimization design of steel truss beam based onsystem reliability[J]. Journal of Central South University (Science and Technology), 2014, 45(10): 1331?1335.

[17] 陳曦, 譚冠政, 江斌. 基于免疫遺傳算法的移動機器人實時最優路徑規劃[J].中南大學學報(自然科學版), 2008, 39(3): 577?583.CHEN Xi, TAN Guanzheng, JIANG Bin. Real-time optimal path planning for mobile robots based on immune genetic algorithm[J]. Journal of Central South University (Science and Technology), 2008, 39(3): 577?583.

[18] 雷英杰, 張善文. 遺傳算法工具箱及應用[M]. 西安: 西安電子科技大學出版社,2014:143?223.LEI Yingjie, ZHANG Shanwen. Genetic algorithm toolbox and its application[M]. Xi’an: Xi’an Universityof Electronic Science and Technology Press, 2014: 143?223.

[19] RUDOLPH G. Convergence analysis of canonical genetic algorithms[J]. IEEE Trans on Neural Networks, 1994, 5(1): 96?101.

(編輯 陳愛華)

Genetic algorithm based homing trajectory planning of parafoil system with constraints

TAO Jin1, SUN Qinling1, ZHU Erlin1, CHEN Zengqiang1, HE Yingping2

(1. College of Computer and Control Engineering, Nankai University, Tianjin 300071, China;2. Aerospace Life-Support Industries Ltd,Aviation Industry Corporation of China, Xiangyang 441003, China)

Homing trajectory planning of parafoil system is a kind of optimal control problem with constraints, a kind of genetic algorithm with elite strategy to solve such a problem was introduced. For the convenience of using genetic algorithm, the non-uniform B-spline was adopted to characterize the control law, so as to transform the optimal control problem into a control vertices of B-spline basis function optimization problem. In view of homing terminal equality constraints which can be converted into inequality constraints by relaxation factors, a static penalty function method was introduced. The normalized model under two different initial conditions was simulated, and three kinds of relaxation factors were set according to landing accuracy requirements of practical engineering. The simulation results show that the control information of homing trajectory is reasonable, and it is an effective method which is suitable for practical engineering demands.

parafoil system; homing trajectory planning; genetic algorithm; penalty function; constraints handling; relaxation factor

10.11817/j.issn.1672?7207.2017.02.019

V249；TP13

A

1672?7207(2017)02?0404?07

2016?04?11；

2016?06?29

國家自然科學基金資助項目(61273138)；天津市重點基金資助項目(14JC2DJC39300)(Project(61273138) supported by the National Natural Science Foundation of China; Project(14JC2DJC39300) supported by the Key Fund of Tianjin Municipal)

孫青林，教授，博士生導師，博士，從事自適應控制、嵌入式控制系統和柔翼無人機導航、制導和控制等方面的研究；E-mail：sunql@nankai.edu.cn