強非線性杜芬系統的周期解及其分岔
王旭,李欣業,王振靜,韓善凱
(河北工業大學 機械工程學院,天津 300130)
強非線性杜芬系統的周期解及其分岔
王旭,李欣業,王振靜,韓善凱
(河北工業大學 機械工程學院,天津 300130)
基于廣義諧波平衡法,求解了強非線性杜芬振子自由振動和簡諧激勵下受迫振動的周期-m解,并與數值解進行了比較,從而討論非線性項的系數以及激勵參數對系統周期解的影響.對自由振動而言,倍周期響應的周期是派生系統固有周期的整倍數;對受迫振動而言,倍周期響應的周期是外激勵周期的整倍數.結果表明,為使近似解析諧波解與數值解比較接近,系統的非線性越強,所需的諧波項數越多;所設倍周期分岔解的周期越大,所需的項數也越多.
廣義諧波平衡法;強非線性;杜芬系統;周期-m解
眾所周知,在傳統的求解非線性振動系統的各種近似解析方法中,諧波平衡法是概念最明了、使用最簡便的,且不僅限于弱非線性系統[1-3].也正因如此,許多學者將諧波平衡法與其他方法或理論相結合,提出了新的改進方法,使諧波平衡法的理論有了十分豐富的發展[4].
1981年Lau和Cheung[5]最先將諧波平衡法與增量法結合,并將該方法稱為增量諧波平衡法(IHB法).Yuste[6]將諧波平衡法與雅可比橢圓函數結合起來,得到橢圓函數諧波平衡法.Huseyin等[7]提出了一種把諧波平衡法與多尺度法結合起來的內在的時間多尺度諧波平衡法來分析非線性周期振蕩和分岔問題,在此基礎上,Summers等[8]提出了雙時間尺度諧波平衡法.
早在Lagrange時期,在確定行星運行軌道的演化規律時就提出了平均的概念,后經Krylov和Bogolyubov提出著名的KB變換后,逐步形成了具有嚴格數學理論基礎的平均法[9].Chow[10]首次在分岔問題中使用了平均法,研究了二維中心流Hopf分岔的穩定性交換公式.平均法經過徐兆和張佑啟等多位學者的不斷完善,逐步發展為廣義平均法[11].在此基礎上又加入廣義諧波函數的概念,通過這種處理平均法不但可以用于求弱非線性問題,對強非線性系統也同樣適用.
廣義諧波平衡法[12]綜合了諧波平衡法和平均法的優勢,既是諧波平衡法的發展,又是平均法的發展.本文將基于此法構造杜芬系統自由振動和受迫振動的近似解析周期解.由于篇幅限制,略去了對基于此法構造的周期解的穩定性分析.
1 廣義諧波平衡法
考慮如下形式的運動微分方程
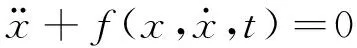
(1)
與諧波平衡法類似,設其解的形式如下:
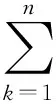
(2)
當該方程為自治系統時,其基頻Ω是對應的線性系統的固有頻率.當該方程為非自治系統時,對應的是外激勵周期的整數倍,與平均法類似,式(2)中的諸系數是時變的.對式(2)求二階導數,可得
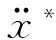
(3)
將式(3)代入方程(1),再利用三角函數的正交性可得
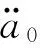
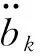
(4)
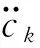
其中
式(4)又可以改寫成如下一階微分方程組的形式:
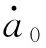
(5)
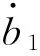
?
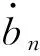
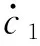
?
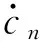
式(5)是用于確定近似解(2)的平均方程,若令z=(a0,b1,…,bn,c1,…,cn)T,又可寫成如下形式:
(6)
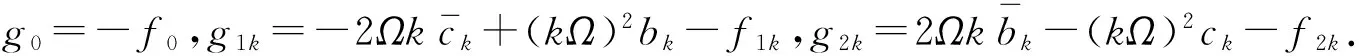
與平均法類似,為求形如式(2)的穩態解,令各平均方程等號右邊的表達式為零,可得到關于諸系數的2n+1個非線性代數方程組
(7)
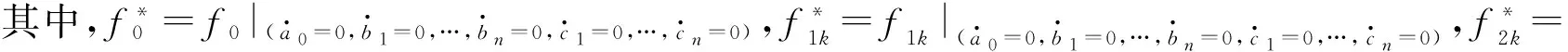
一般地,式(7)可以通過Newton-Raphson方法進行數值求解.根據李雅普諾夫一次近似理論,可以通過求相應雅克比矩陣的特征值來判斷解的穩定性.
2 杜芬系統自由振動的周期解
在不考慮阻尼的情況下,杜芬系統的自由振動微分方程可以表示為
(8)
相應的平均方程為
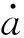
(9)
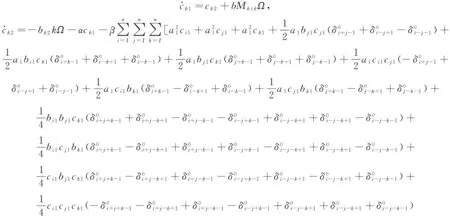
圖1和圖2分別表示在α、β取不同值時,x的近似解析解和數值解的時間歷程曲線,其中圖例xn表示數值解,xa表示近似解析解,下角標中的數字代表諧波項的項數.
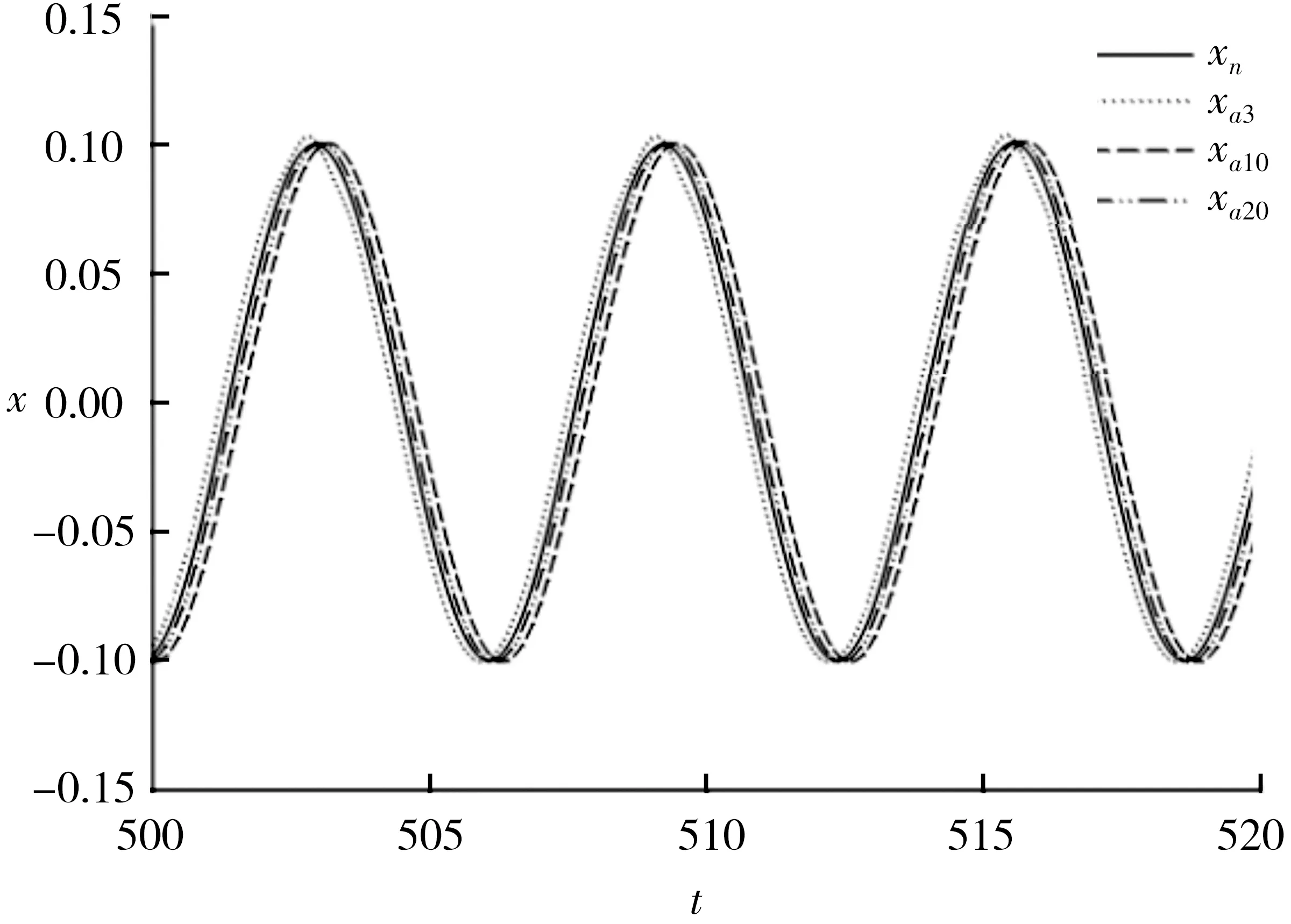
圖1 α=1,β=0.1時的時間歷程Fig.1 Time history with α=1,β=0.1
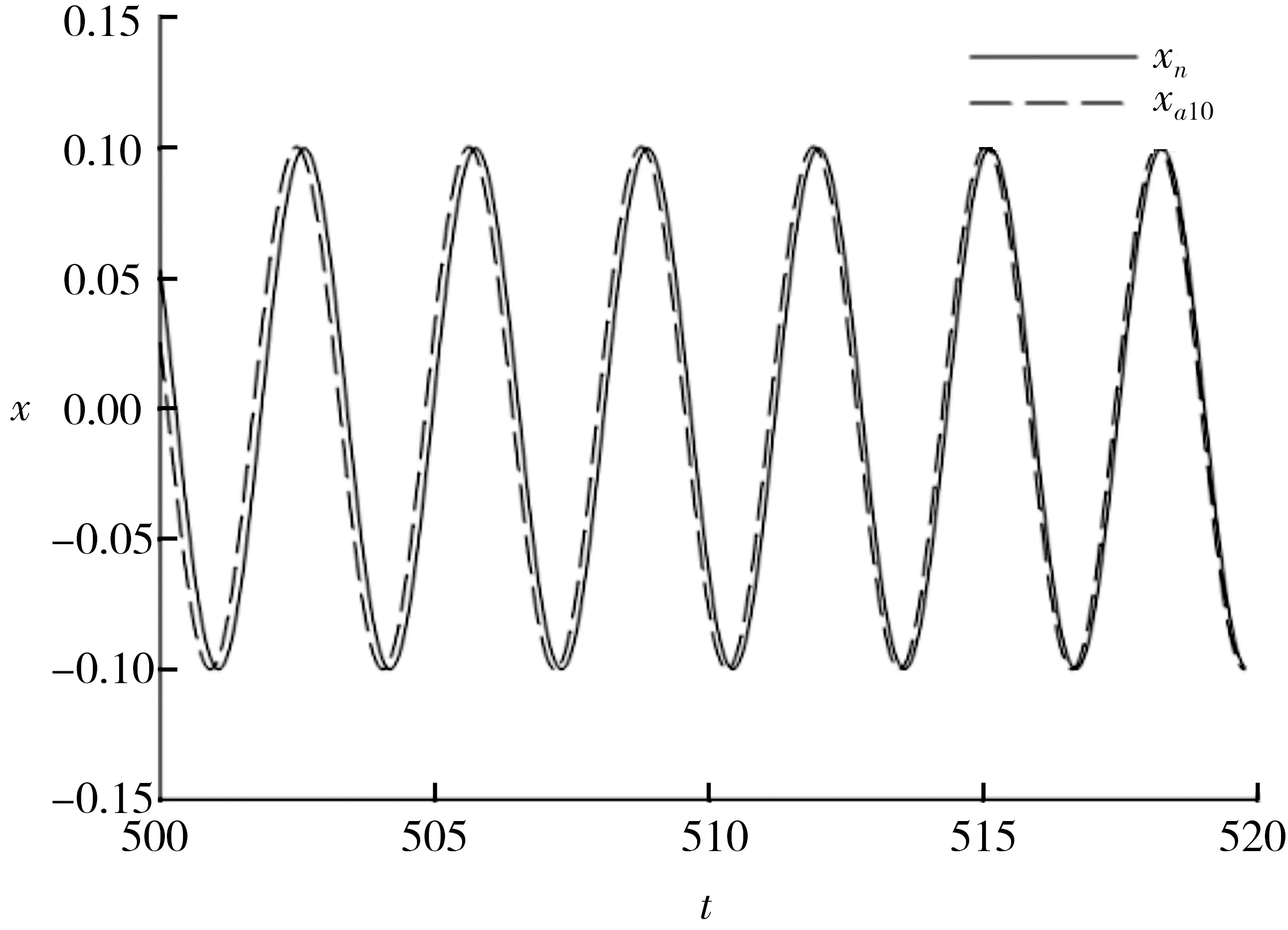
圖2 α=4,β=5時的時間歷程Fig.2 Time history with α=4,β=5
圖1表明,當非線性較弱時,用3項諧波的和作為近似解就能較好地與數值解吻合,繼續增加諧波項的項數,對提高解的精度意義不大.圖2表明,當系統的非線性較強時,由于派生系統的固有周期變小,用10項諧波的和作為近似解也能較好地與數值解吻合.所以在接下來討論杜芬系統的受迫振動時,近似解是按至少包含10項諧波給出的.
3 杜芬系統受迫振動的周期解
在自由振動基礎上,以杜芬系統的受迫振動為例,驗證廣義諧波平衡法對周期-m解的適用性.
3.1 周期-m解
杜芬系統的受迫振動微分方程可以表示為
(10)
設其解為
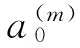
(11)
此時的平均方程為
n.
(12)
將式(12)簡寫成
(13)
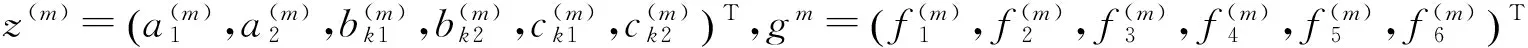
g(m)(z(m))=06×1.
(14)
此時得到的平衡點即為近似解析解,即方程(10)中動力學系統的穩態解.
3.2 激勵參數的影響
強非線性杜芬系統在作受迫振動時可能出現倍周期分岔的情況,以隨外激勵幅值和外激勵頻率變化而產生的倍周期分岔為例,對廣義諧波平衡法求解周期-m解的適用性進行分析.
3.2.1 激勵幅值的影響
圖3和圖4分別為μ=0.3,α=-1,β=1,Ω=1.2時,不同的F值對應的x的時間歷程曲線.
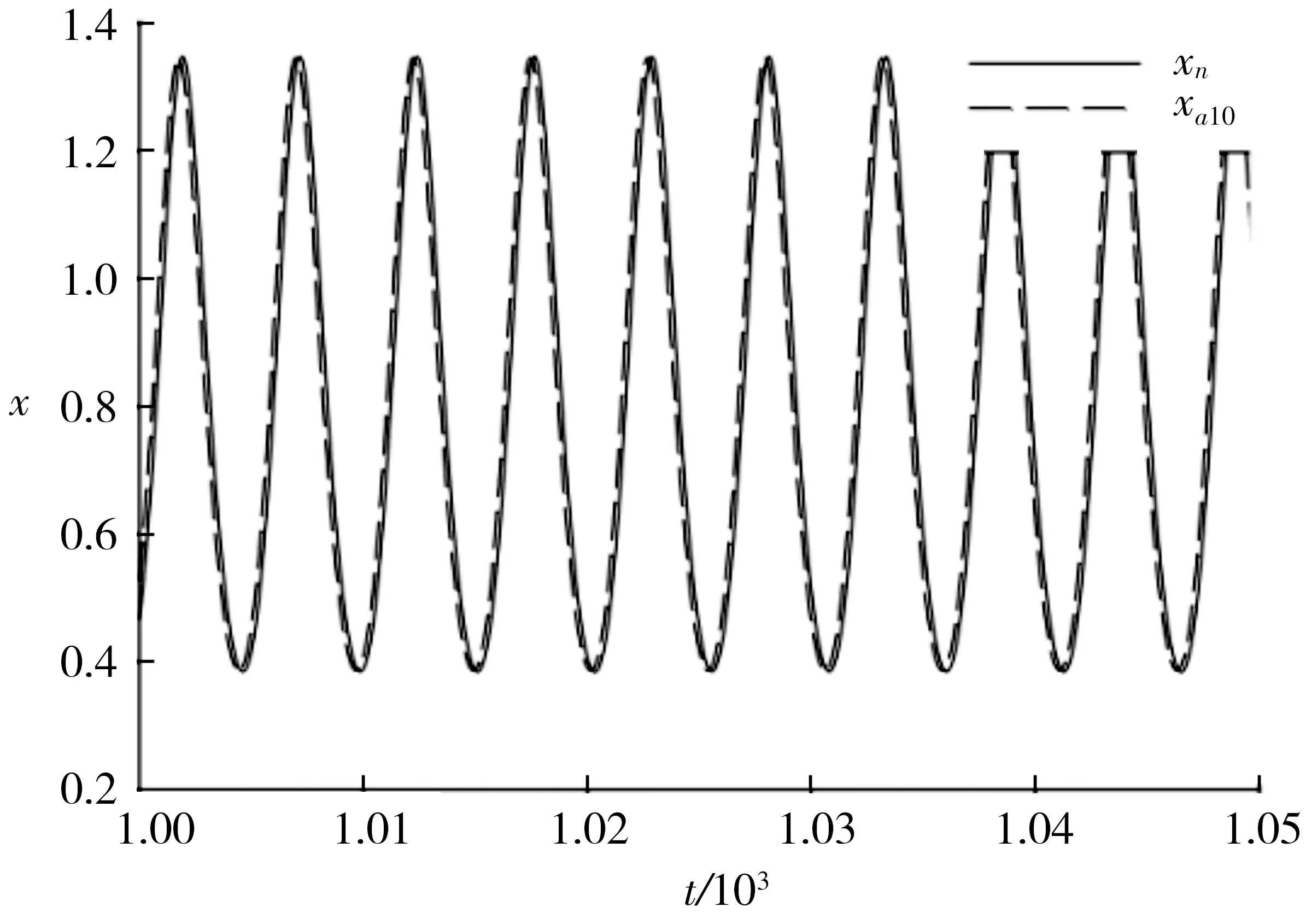
圖3 F=0.2時的時間歷程Fig.3 Time history with F=0.2
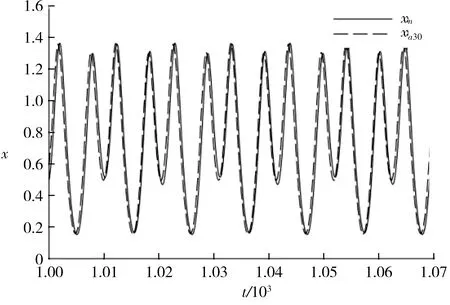
圖4 F=0.287時的時間歷程Fig.4 Time history with F=0.287
與圖3對比,圖4表明系統的受迫振動響應周期為圖3所示響應周期的2倍.
3.2.2 激勵頻率的影響
圖5、6、7分別表示方程(9)中選取μ=0.25、α=-1、β=1、F=0.26時隨Ω值的變化,響應出現倍周期分岔時,x的時間歷程曲線.
圖5—圖7表明,隨著外激勵頻率的減小,受迫振動響應出現了倍周期分岔,即響應周期倍增的現象.由于周期不斷變大,所以近似解中的諧波項數越來越多,以期能與數值解有比較好地吻合.
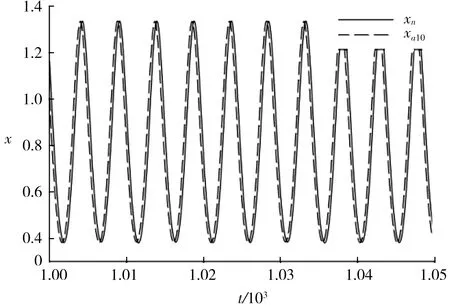
圖5 Ω=1.3時的時間歷程Fig.5 Time history with Ω=1.3
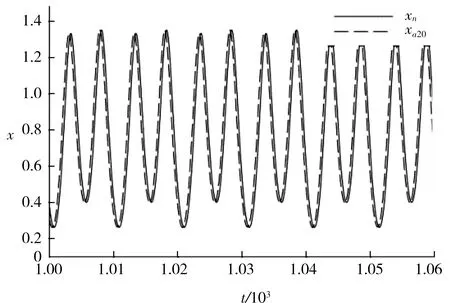
圖6 Ω=1.24時的時間歷程Fig.6 Time history with Ω=1.24
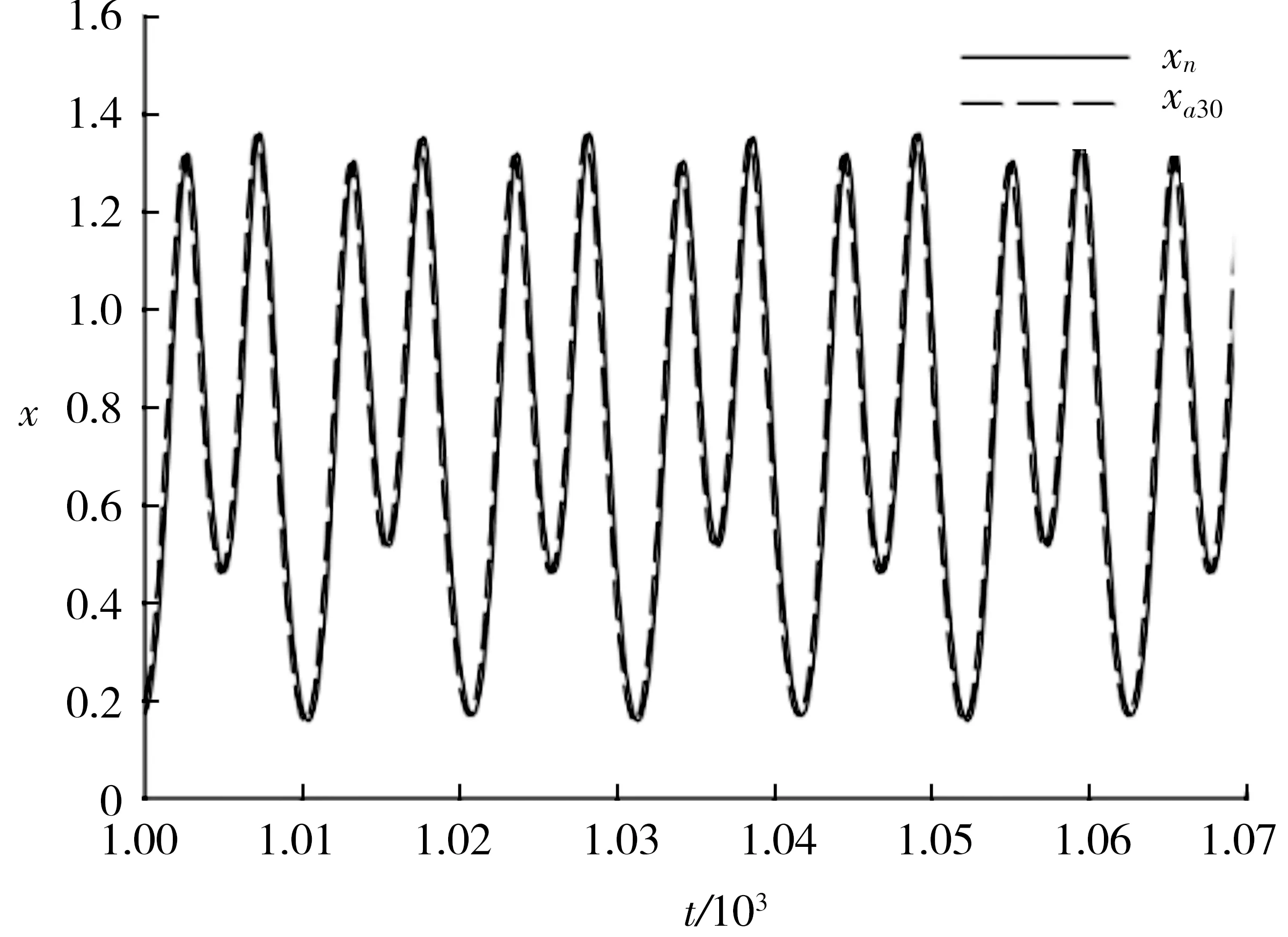
圖7 Ω=1.2時的時間歷程Fig.7 Time history with Ω=1.2
4 討論與結論
廣義諧波平衡法結合了諧波平衡法和平均法的優點,即不僅可以進行解的穩定性分析,又適用于強非線性系統,亦適用于多自由度系統.本文利用此法求解強非線性杜芬系統的近似周期解時,僅考慮了倍周期分岔的情況,即對自由振動,僅考慮了周期為派生系統固有周期整倍數的情況,對受迫振動僅考慮了周期為外激勵周期整倍數的情況.對于受迫振動而言,這種倍周期運動相當于亞諧振動.事實上,也可用此法求強非線性系統的超諧振動解,即解的周期為派生系統固有周期(對自由振動)或激勵周期(對受迫振動)的幾分之一倍的情況.本文的結果表明,不論是自由振動還是受迫振動,只要所需諧波項數足夠多,基于此法構造的近似解析解都能很好地與數值解吻合.為使近似解析諧波解與數值解比較接近,則系統的非線性越強,所需的諧波項數越多;所設倍周期解的周期越大,所需的項數也越多.
[1] 陳予恕.非線性振動[M].北京: 高等教育出版社,2002.
[2] 陳予恕.非線性振動、分岔和混沌理論及其應用[J].振動工程學報,1992,5(3): 235-250.DOI:10.16385/j.cnki.issn.1004-4523.1992.03.009.
[3] 劉延柱,陳立群.非線性振動[M].北京: 高等教育出版社,2001.
[4] CHEN Y M,LIU J K.A new method based on the harmonic balance method for nonlinear oscillator [J].Physics Letters A,2007,368(5): 371-378.DOI:10.1016/j.physleta.2007.04.025.
[5] LAU S L,CHEUNG Y K.Amplitude incremental variational principle for nonlinear of elastic systems[J].Journal of Applied Mechanies,1981,48: 959-964.DOI: 10.1115/1.3157762.
[6] YUSTE S B.Comments on the method of harmonic-balance in which Jacobi elliptic function are used[J].Journal of Sound and Vibration,1991,145(3): 381-390.DOI: 10.1016/0022-460X(91)90109-W.
[7] HUSEYIN K,LIN R.An intrinsic multiple-scale harmonic balance method for nonlinear vibration and bifurcation problems[J].International Journal of Non-linear Mechanics,1991,26: 727-740.DOI: 10.1016/0020-7462(91)90023-M.
[8] SUMMERS J L,SAVAGE M D.2 timescale harmonic-balance.I.Application to autonomous one-dimensional nonlinear oscillators[J].Philosophical Transactions of the Royal Society A,1992,3: 340-473.DOI: 10.1098/rsta.1992.0077.
[9] 張琪昌,王洪禮.分岔與混沌理論及應用[M].天津: 天津大學出版社,2005.
[10] CHOW,S N,MALLER-PARET.Integral averaging and bifurcations[J].Differential Equations,1977,26: 112- 159.DOI: 10.1016/0022-0396(77)90101-2.
[11] CHEUNG Y K,XU Z.Intemal resonance of strongly non-linear autonomous vibrating systems with many degrees of freedom[J].Journal of Sound and Vibration,1995,180(2): 229-238.DOI:10.1006/jsvi.1995.0076.
[12] ALBERT C,LUO J.ARASH BAGHAEI LAKEH.Period-m motions and bifurcation trees in a periodically forced van der Pol-Duffing oscillator[J].International Journal of Dynamics and Control,2014,2(4):474-493.DOI: 10.1007/s40435-014-0058-9.
(責任編輯:王蘭英)
PeriodicsolutionsandtheirbifurcationofDuffingsystemwithstrongnon-linearity
WANGXu,LIXinye,WANGZhenjing,HANShankai
(School of Mechanical Engineering,Hebei University of Technology,Tianjin 300130,China)
Based on the generalized harmonic balance method,the period-m responses of free and forced Duffing oscillators are constructed and compared with numerical solutions from which the effects of nonlinear term and excitation parameters can be observed.For free vibrations,the response periods are assumed to be integer times of the natural period of the corresponding linear system and the excitation period respectively.It is shown that the number of harmonic terms should be large enough for both strongly nonlinear systems and period-doubling bifurcation solutions with large period so that the approximate analytic solutions are comparative to numerical results.
generalized harmonic balance method;strong non-linearity;Duffing systems;period-msolution
O322
A
1000-1565(2017)05-0457-07
10.3969/j.issn.1000-1565.2017.05.003
2017-03-27
河北省高層次人才資助項目(C201400309)
王旭(1990—),男,河北保定人,河北工業大學在讀碩士研究生.E-mail:1216380802@qq.com
李欣業(1966—),男,河北遷安人,河北工業大學教授,主要從事復雜系統的動力學建模與分析和非線性動力學與控制研究.E-mail:xylihebut@163.com

