解讀中小學數學教學的銜接點

斯翠梅

長期以來，中小學數學教育各自為陣、相互脫節的現象普遍存在。學生在小學數學中接觸的都是較為直觀、簡單的基礎知識，而升入初中后，所學知識在抽象性、嚴密性上都有一個飛躍，此時，一些學生不能夠很快地適應中學的學習方式和學習內容，因為缺乏足夠的心理準備而造成學習成績的下降，甚至會產生厭學怕學、緊張焦慮的不良反應。因此，小學高段教師就需要參考中學的目標和內容，來構建小學高年級數學教學的體系，以發展的眼光看待學生的成長，加強與七年級各方面的銜接，幫助六年級學生順利邁向新階段的學習。那么，從小學進入中學數學教學的要求與內容有什么差異呢？中小學數學知識從橫向、縱向兩方面發展，變化十分明顯，這要求教師應當明確知識間的內在聯系，掌握新舊知識的銜接點，才能在教學中做到有的放矢。

從“算術數”到“有理數”

學生剛升入七年級，首先接觸到了一個新領域的計算——負數的計算。負數的概念在小學六年級第二學期出現，但只是初步了解，并不涉及負數的計算。因此在正式介入負數概念時，可以結合生活中的實際問題提出。比如，測量溫度，當氣溫在零度以上時，學生能用之前所學的數表示其溫度的高低，但當氣溫在零度以下時，就難以用之前所學的知識表示了。結合這些問題，引入負數表示兩個具有相反意義的量，并適當介紹有理數、無理數的概念，使學生感受到數的概念是為解決實際問題的需要而逐漸發展的。

從“數”到“式”的過渡

用字母表示數，實際上是數的概念及其運算法則抽象化、公式化的過程。學生要經歷由算術到代數的過渡，主要體現為由數過渡到用字母表示數。字母是代表數的，但它不代表某個具體的數，這種特殊的關系正是七年級學生學習的困難所在。為了克服七年級新生對這一轉化而引發的學習障礙，教學中，教師要從小學學過的用字母表示數的知識入手，盡量用一些字母表示數的實例，自然而然地引出代數式的概念。如在人教版五年級上冊的第四單元就有《簡易方程》一塊內容，其中包含用字母表示數、利用天平原理（等式的基本性質）、用方程解決數學問題等教學內容。在教學中，教師既要有意識地穿插利用運算的性質解方程，同時將重點放在用方程解決問題上，由此為學生在后續學習代數搭建了穩定的橋梁，進而降低學生的學習難度。

由“算式”到“方程”的過渡

列方程解應用題是七年級數學的難點。在七年級講授列方程解應用題時，審題最關鍵，要設法弄清題意，找出能夠表示應用題全部意義的等量關系。

因此，在小學階段的實際講授過程中，應當結合教材的安排，有意識地引導學生寫出等量關系，并利用等量關系列出方程。另外，嘗試利用線段圖、列表格的方式等進行分析，這樣會降低列方程的難度。在教學中，通過算術方法和列方程的方法對比，讓學生進一步明確，有些問題用算術解題不方便，凸顯列方程解應用題的優越性，培養學生列方程解應用題的意識。

實驗幾何到論證幾何的過渡

小學教材中，幾何知識偏重于計算和具象思維，局限于量一量、畫一畫、拼一拼、折一折及簡單地套用公式計算。小學幾何重計算不重邏輯推理，不重視抽象思維。而中學的幾何，由已知幾何體抽象出幾何圖形。小學只要求學生對一些幾何圖形的性質及結論記住就可以了，而中學則要求學生在實驗得出結論的基礎上，還要從理論上給予證明。對學生的能力提出了新的要求，不僅應具有動手操作的能力，同時還應具備推理論證的能力。

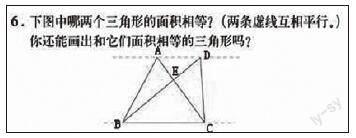
比如，人教版五年級上冊教材第87頁的練習十六中，有這樣一道習題：

師：為了描述方便，我們在三角形的頂點標上字母，然后順次用字母描述。比如△ABC。圖中哪兩個三角形的面積相等呢？

生1：△ABC和△BCD。

師：你能說明理由嗎？

生1：因為兩個三角形的底相同，高也相同。

師：聽懂得請舉手（超過70%的同學舉起了手）。那我們一起來描述一下。△ABC和△BCD的底都是BC，因為AD與BC平行，所以高也相等——平行線間的距離處處相等。所以△ABC和△BCD的面積都相等。這里還有相等面積的三角形嗎？

生2：△ABE和△CDE的面積相等。

師：你能說出理由嗎？

生2：大的兩個三角形面積相等，減掉一個相同的三角形，剩下的也相等。

師：說得真好。因為△ABC和△BCD的面積相等，所以△ABC—△BCE和△BCD—△BCE的面積也相等，即△ABE和△CDE的面積相等。

本例題中有蘊涵著幾何的轉化思想，教師通過自己的指導，幫學生理清思路，為初中的后續學習打下了基礎。

加強中小學銜接已成為新課程下的共識，教師要明確小學高段和初中知識間的內在聯系，掌握新舊知識的銜接點，考慮到學生生理與心理發展的漸進性，認真分析研究中小學學生數學學習方法與思維習慣方面的差異，正確引導學生做好從小學數學到初中數學的過渡。