基于噪聲抵消技術的時延估計

郭昕鈺，劉嘉琦，王良，宋志杰

?

基于噪聲抵消技術的時延估計

郭昕鈺，劉嘉琦，王良，宋志杰

(中國海洋大學信息科學與工程學院，山東青島266100)

闡述了噪聲抵消時延估計法(Time Delay Estimation based on Noise-canceling，TDENC)的基本原理，建立了TDENC分析的估計模型；并進行了大量仿真計算和初步海上試驗。仿真結果表明：低信噪比且干擾噪聲間相關性較強時，TDENC估計延時明顯優于常規方法，但其主峰較寬；干擾噪聲間彼此相關但信噪比高，估計時延精度則較差。海上試驗結果和理論仿真一致。

時延估計；噪聲抵消；最小均方誤差；反轉修正算法

0 引言

常規相關法是經典的時延估計方法，該方法利用相關函數峰值估計信號之間的延遲時間差，人們在不同方面做了大量研究工作[1-4]。在白噪聲背景下，常規時延估計是最佳估計；而存在相關噪聲時，常規估計性能變差。廣義相關法[5]在對信號進行相關運算之前，對信號進行了加權處理；提高信噪比較高的信號頻率成分，抑制低信噪比的信號頻率成分，以達到提高信號整體信噪比的目的，最終提高時延估計的精度。B Widrow等[6]提出的自適應時延估計算法可以克服廣義相關時延估計法加權固定的局限性。景思源等[7]根據平面四元法目標定位計算式，研究發現廣義互相關時延估計算法具有精度高、穩定性好的特點。自適應時延估計算法可自動調節濾波器結構以及濾波器參數以達到最優準則[7-10]。

本文基于噪聲抵消理論，提出一種新的時延估計方法——噪聲抵消時延估計法(Time Delay Estimation based on Noise-canceling，TDENC)。基于自適應噪聲抵消原理，對于彼此存在一定時延的兩路同源信號，對信號進行抵消，當兩路信號同步時，輸出功率中信號殘差最小，從而抵消后的輸出功率最小，由此獲得時延估計。通過對TDENC的仿真研究和海上實驗數據處理，并與常規估計法進行對比，最后給出結論。

1 理論基礎

1.1 自適應噪聲抵消時延估計法(TDENC)

由文獻[11]可知，自適應噪聲抵消流程如圖1所示。

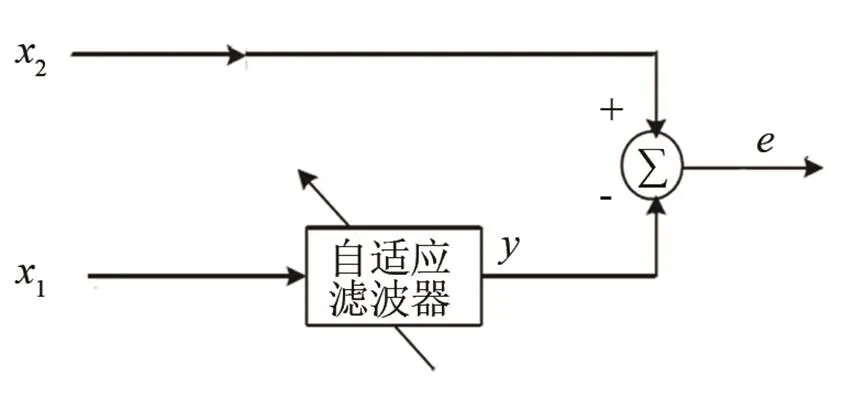
圖1 自適應噪聲抵消流程圖

噪聲抵消誤差為

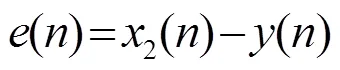
其中，為時間采樣點，均方誤差表示為

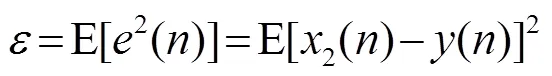
由于

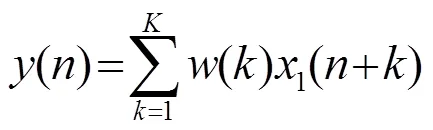
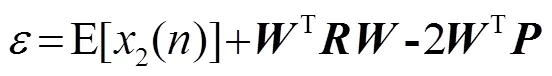
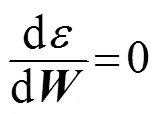
可得最優濾波器設計為

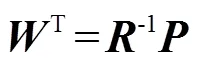
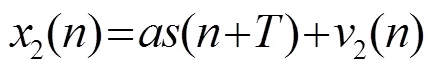
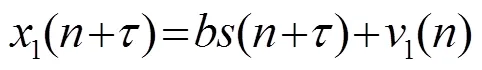
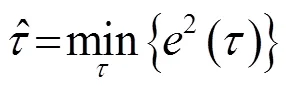
該估計過程中存在兩步優化過程：

時延估計具體做法如下：

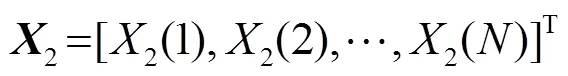
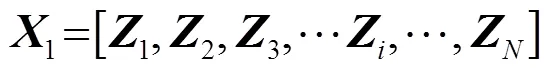
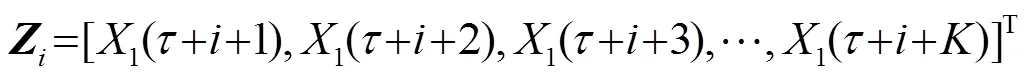
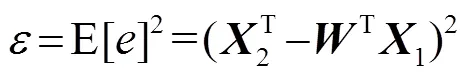
其中權向量為

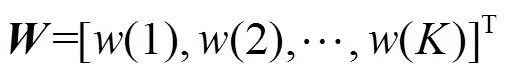
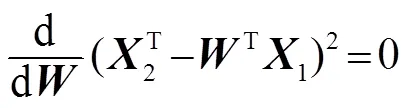
可得最優濾波器為

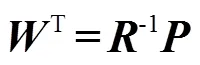
1.2 時延估計修正

由式(4)~(9)可看出，設計濾波器時利用一點對多點的方法進行抵消。由于選取參考點的差異，在估計過程中可能會出現偏移現象。針對這種現象，本文利用時間反轉來修正偏差。修正思路為：對信號進行時間反轉后再進行估計時，估計產生的偏移將會出現在相反方向，再對兩次估計結果取平均處理，偏移即可修正。

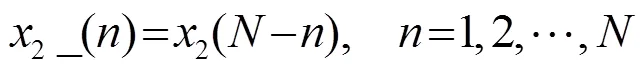
“其他同學的父母因為忙于工作不能到場，你們回去后也可以和父母說一聲‘您辛苦了’，他們也會非常高興的。”

2 數值仿真

本節通過數據仿真研究噪聲抵消原理進行時延估計的性能。仿真條件為：主輸入為1~2 kHz的限帶白噪聲信號，長度為8192點，采樣率為48 kHz。將原始信號進行某一確定時延得到參考信號。為方便顯示，將原始結果減去其最大值，再取絕對值，以使最小值變為最大值。

2.1 反轉修正算法

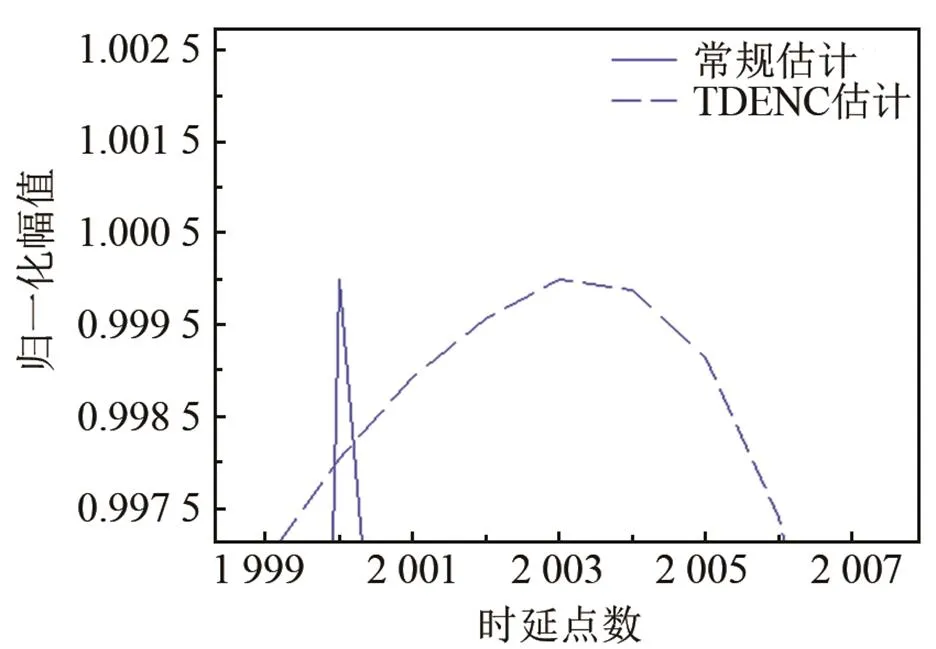
原始算法和反轉算法效果如圖2所示。圖2(a)中，信號時延設置在2 000點，背景噪聲為白噪聲。應用1.1節中的算法進行估計，常規方法最大值點出現的位置為2 000點，TDENC法最大值點出現的位置為2 003點，產生了較大的偏移。圖2(b)給出了應用1.2節中反轉算法的結果。其中，常規方法最大值點出現的位置為2 001點，TDENC法最大值點出現的位置為1996點，平均處理后，得到常規方法最大值在所在的位置為2000.5點，修正后的噪聲抵消法最大值點出現的位置為1999.5點。該結果說明，反轉算法能夠有效修正1.2節中所提到的由于濾波器階數影響所產生的偏移現象。另外，由圖2可知，與常規相關時延估計法相比，在白噪聲背景下，TDENC估計結果圖主峰較寬，相對估計精度較差。該結論與引言中提出的常規相關時延估計在白噪聲背景下為最優估計相一致。

(a) 原始算法

(b) 反轉算法

圖2 原始算法與反轉算法效果圖

Fig.2 Effect drawings of original algorithm and inversion algorithm: (a) original algorithm, (b) inversion algorithm

2.2 噪聲相關性的影響

如果主輸入和參考輸入的長度均為1024點，是幅值為1的白噪聲序列，時延為300點，對兩路信號分別加入存在一定時延的相同白噪聲序列作為相關干擾，相關干擾長度為256個點，是局部干擾，幅值為1.5，存在時延為310個點。再引入兩路非同源白噪聲作為背景噪聲，幅值為0.2。噪聲抵消時延估計算法中，濾波器階數為5。

圖3為常規相關時延估計和TDENC性能對比圖。由圖3可知，當存在相關噪聲時，常規時延估計法受噪聲影響較大，圖3(c)為峰值所在位置的局部放大圖，由于受到相關噪聲影響，常規估計發生較大偏移，最大值出現在309點，利用TDENC進行估計時，最大值點出現在303點，相比于常規方法，偏移量更小。由此可知，TDENC可以有效減小相關噪聲對估計結果的影響，提高了時延估計的準確度。

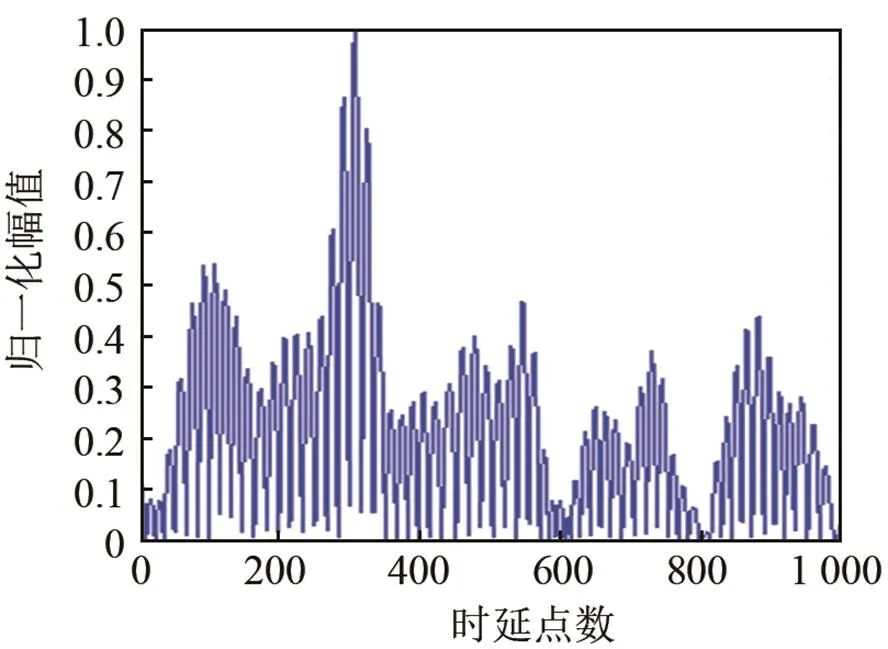
(a) 常規方法

(b) TDENC方法

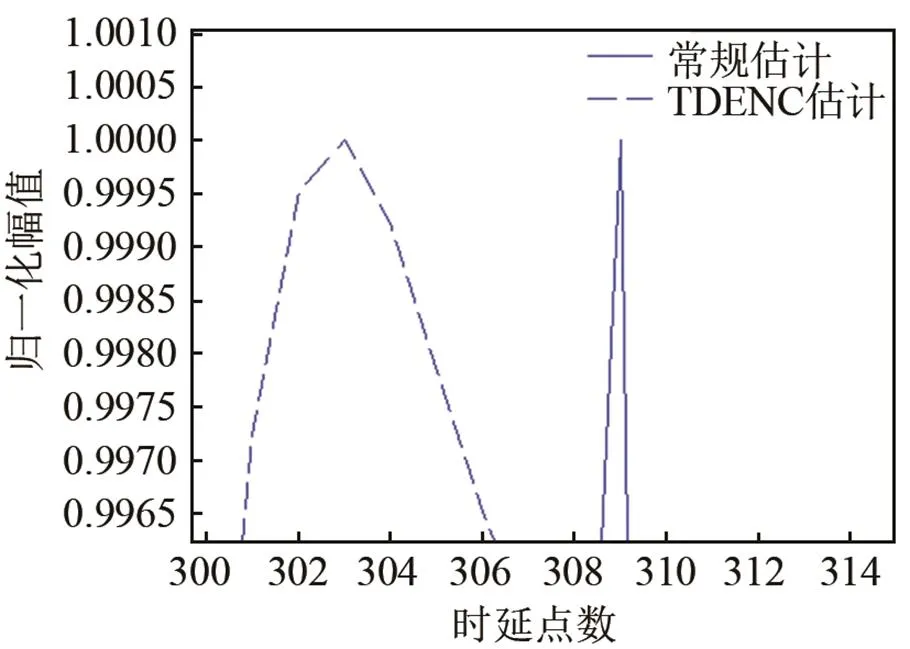
(c) 常規方法和TDENC方法時延估計性能對比圖

2.3 帶寬影響

將白噪聲分別經4~5 kHz和2.5~6.5 kHz帶通濾波后產生中心頻率相同、帶寬不同的兩種限帶信號，再將其一經2 000點延時構成兩組信號，對其進行噪聲抵消時延估計。

由圖4可知，TDENC對帶寬較寬信號的估計性能明顯優于帶寬較窄信號。在縱坐標處于半功率點(即0.5)時，1 kHz帶寬對應的主峰半寬度為71個點，4 kHz帶寬對應的主峰半寬度為23個點，主峰寬度隨帶寬增大而減小，同時，信噪比明顯提高，從而提高了時延估計精度及穩定性。由此可見，TDENC法對寬帶信號有較好的估計性能，得到了與1.1節中理論分析一致的結論。

(a) 帶寬為1 kHz

(b) 帶寬為4 kHz

圖4 帶寬對TDENC結果的影響

Fig.4 The influences of bandwidth on TDENC results

3 實驗數據處理

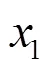
3.1 常規相關法與噪聲抵消法處理結果對比

分別采用常規相關和TDENC處理某一時刻數據，信號頻段為1~8 kHz，信號長度為1 024點，濾波器階數為8階。實驗中存在兩個目標，目標1位于時延500點附近，較弱的目標2位于時延700點附近。

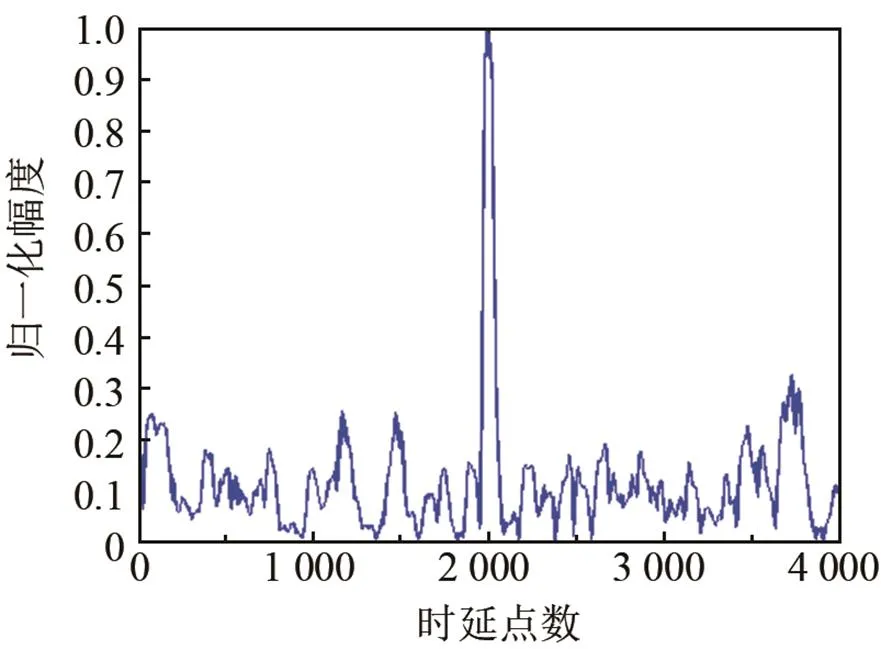
圖5為320 s時，常規相關法和TDENC性能對比圖，橫坐標為時延點數，縱坐標為歸一化后的幅值。由圖5可知，當噪聲相關性較強時，用常規方法進行估計時會出現較多虛警，難以準確識別。TDENC能較好抑制相關噪聲，減少了虛警。圖5(a)中，時延700點附近目標被淹沒，在1400點、900點、250點附近出現較多虛警。圖5(b)中，利用TDENC能有效抑制相關噪聲，獲得較高的信噪比處理增益，較準確估計出兩個目標的時延點數。

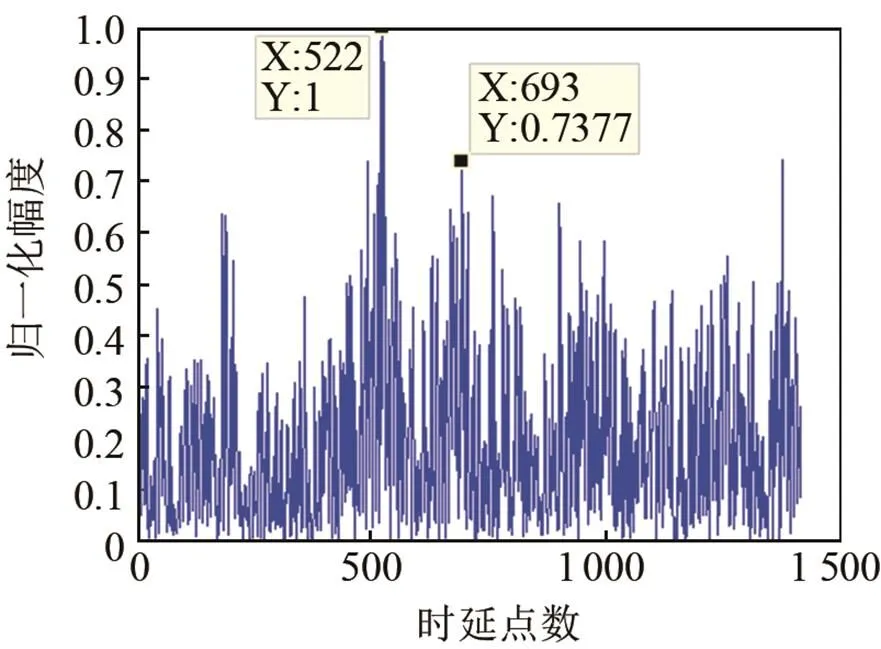
(a) 常規相關法

(b) TDENC估計性能對比圖

圖5 某一時刻(a)常規相關法和(b)TDENC估計性能對比圖

Fig.5 Comparison charts of estimation performance (a) conventional correlation method, (b) TDENC

3.2 常規相關法與噪聲抵消法估計精度對比圖

選取某一時刻的數據，研究對目標2的估計精度，如圖6所示。

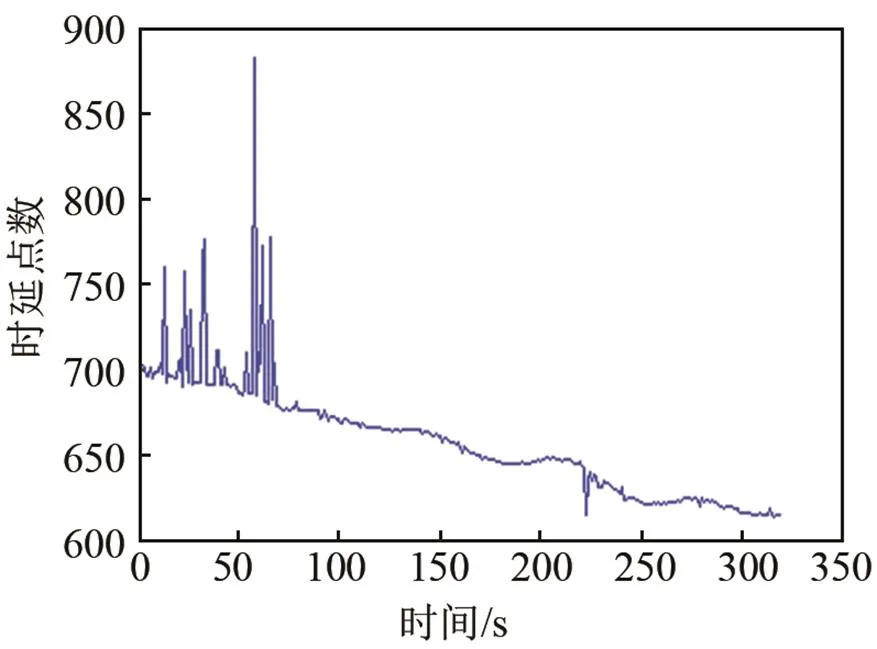
(a) 常規相關法

(b) TDENC方法

圖6 (a) 常規相關法與(b) TDENC時延估計結果隨時間變化圖

Fig.6 Variation of time delay estimation results with time (a) conventional correlation method, (b) TDENC

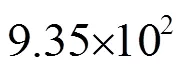
圖7為截取前90 s兩種估計結果歷程圖，圖中20 s時刻對應的波形圖見圖5。由圖7中可以明顯看出，當存在較強的相關噪聲干擾時，常規估計效果較差，目標淹沒在背景噪聲中，難以分辨。TDENC則能有效抑制相關噪聲，獲得較大的信噪比增益，使估計性能穩定，目標更加清晰。

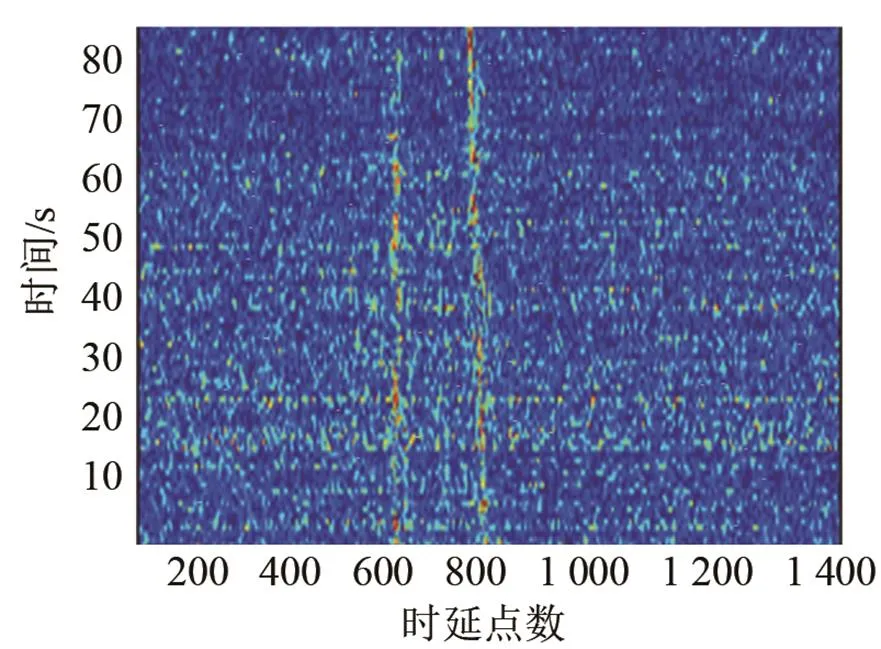
(a) 常規估計

(b) TDENC估計

圖7 前90 s歷程圖(a) 常規估計(b) TDENC估計

Fig.7 Processing maps in the first 90 s (a) conventional correlation method, (b) TDENC

4 結論

本文以噪聲抵消技術為理論基礎，設計了一種時延估計方法——TDENC估計法。針對接收信號中存在相關噪聲而導致常規相關時延估計性能變差的情況，TDENC能有效抑制相關噪聲，從而提高時延估計精度。

本文通過仿真實驗與海上數據處理，得出以下結論：

(1) TDENC對寬帶信號有較好的處理結果，帶寬越寬，估計性能越好。在3.3節仿真條件下，帶寬增加為原來的4倍，主峰半寬度減少了67.6%。

(2) 相比常規檢測，當噪聲相關性較強時，TDENC方法能更有效地抑制相關噪聲，獲得更大的信噪比處理增益，提高時延估計精度。

(3) 高信噪比條件下，TDENC方法比常規方法時延估計精度低，表明它更適用于信噪比較低且干擾噪聲相關性較強條件下的時延估計。在文中的海試條件下，性能提高了63.7%。

[1] Knapp C H, Carter G C. The generalized correlation method for estimation of time delay[J]. IEEE Trans. Acoust, Speech, Signal Processing, 1976, 24(8): 320-327.

[2] Messer H, Shor G. Passive time delay estimation in non-gaussian noise[J]. IEEE Trans, 1999, 7(9): 2531-2534.

[3] Xiao Lai, Hans Torp. Interpolation methods for time-delay estimation using cross-correlation method for blood velocity measurement[J]. IEEE Trans on Ultrasonics, Ferroelectrics, and Frequency Control, 1999, 46(2): 277-289.

[4] Stephenne A, Champagne B. A new cepstralperfiltering technique for estimating time delay under reverberant conditions[J]. IEEE Trans, 1997, 59(3): 253-266.

[5] 行鴻彥, 趙守國, 邸繼征, 等. 廣義相關時延估計算法的自適應實現形式[J]. 西安石油學院學報(自然科學版), 2001, 16(6): 47-51. XING Yanhong, ZHAO Shouguo, DI Jizheng, et al. Adaptive realizing form of generalized algorithm for time delay estimation[J]. Journal of Xi’an Petroleum Institute(Natural Science Edition), 2001, 16(6): 47-51.

[6] Widrow B, Steam S D. Adaptive signal processin[M]. Englewood. Cliffs: Prentice-Hall. Inc. 1993.

[7] 景思源, 馮西安, 張亞輝. 廣義互相關時延估計聲定位算法研究[J]. 聲學技術, 2014, 33(5): 464-468. JING Siyuan, FENG Xi’an, ZHANG Yahui. Study of a generalized crosscorrelation time delay estimation based acoustic positioning algorithm[J]. Technical Acoustics, 2014, 33(5): 464-468.

[8] 詹國強, 吳正國. 一種新的變步長LMS自適應濾波算法[J]. 海軍工程大學學報, 2006, 18(2): 109-112. ZHAO Guoqiang, WU Zhengguo. Anovel variable step size adaptive filtering LMS Algorithm based on sample function[J]. Journal of Naval University of Engineering, 2006, 18(2): 109-112.

[9] 馮桂, 張繼賢. 噪聲的分布層次分析及其自適應濾波算法[J].測繪科學, 2000, 25(3): 12-13. FENG Gui, ZHANG Jixian. The study of noise hierarchical distribution and corresponding adaptive filtering algorithms[J]. Science of Surveying and Mapping, 2000, 25(3): 12-13.

[10] Chang C Y, Shyu K K. Active noise cancellation with a fuzzy adaptive filtered-x algorithm[J]. IEE Proc. Circuits Devices Syst. 2003, 150(5): 416-422.

[11] 曹斌芳. 自適應噪聲抵消技術的研究[D]. 長沙: 湖南大學, 2007. CAO Binfang. Research on adaptive noise cancelling technology[D]. Changsha: Hunan University, 2007.

Time delay estimation based on noise-canceling

GUO Xin-yu, LIU Jia-qi, WANG Liang, SONG Zhi-jie

(College of Information Science and Engineering, Ocean University of China, Qingdao 266100,Shandong, China)

A time delay estimation method based on noise canceling called TDENC (Time Delay Estimation based on Noise-Canceling)is proposed to improve the time delay estimation performance when the background noise is correlative. A TDENC model is formed firstly in this paper, and then computer simulations are carried out to study the performance and applicable range of TDENC. Simulation results show thatin the case of low SNR and strong correlation between noises, TDENC method is obviously superior to the conventional methods, but the main lobe is broad. However, when SNR is high, the performance of TDENC is worse than the conventional method. The experimental data processing results agree well with the simulation.

time delay estimation; noise-canceling; Minimum Mean Square Error(MMSE); inversion correction algorithm

TN911.7

A

1000-3630(2017)-02-0177-06

10.16300/j.cnki.1000-3630.2017.02.014

2016-07-29; 修改日期:2016-10-22

郭昕鈺(1993－), 女, 山東東營人, 碩士研究生, 研究方向為水聲信號處理。

郭昕鈺, E-mail: 453237740@qq.com。