基于Lorenz混沌調頻的水下正交波形集設計

田晶，陳航,2，唐鏡治，滕舵,2

?

基于Lorenz混沌調頻的水下正交波形集設計

田晶1，陳航1,2，唐鏡治1，滕舵1,2

(1. 西北工業大學航海學院，陜西西安710072；2. 水下信息處理與控制國家重點實驗室，陜西西安710072)

針對網絡水下航行器組聯合探測情況下各網絡節點間信號會互相干擾的問題，基于Lorenz混沌模型，提出一種混沌調頻(Chaos Frequency Modulation，CFM)的正交波形集設計方法。首先建立基于Lorenz序列的CFM信號模型，對其進行相關特性分析和正交特性研究，包括CFM正交波形集的個數和波形長度對波形集正交性能的影響，提出對混沌序列進行加窗函數處理的CFM波形集正交性優化方法；然后構造網絡水下航行器組分別發射線性調頻(Linear Frequency Modulation，LFM)信號和CFM信號的回波模型，對比分析了匹配濾波器對回波信號的處理結果。仿真結果表明，該設計方法簡便、靈活、高效，產生的CFM正交波形集性能良好，且相對于常規信號在水下信號檢測方面具有明顯的優勢。

混沌序列；頻率調制；正交波形集；網絡水下航行器

0 引言

網絡水下航行器是一種高度信息化、網絡化的航行器組群，具有多輸入多輸出、位置分布式的特點。同時，水聲信道是一個極其復雜的隨機時間-空間-頻率參變信道，可能受到窄帶、高噪、多途、強干擾和傳輸損耗等眾多因素的制約。對于各網絡水下航行器節點來說，若是采用常規信號作為發射信號，各節點的信號會形成相互干擾，不僅降低了信噪比，還使得目標檢測能力變弱，給信號處理造成極大的困難。這就要求各網絡水下航行器節點間的發射信號必須具有正交性，各節點發射通道相互獨立，以獲得空間分集增益。因此，基于水下網絡航行器的正交波形集設計具有重要意義。

正交波形集需要具備兩個條件，一是具有良好的脈沖壓縮性能，即自相關函數近似于沖擊函數，二是波形間應具有盡量低的互相關性。由于混沌序列具有與沖擊響應函數相類似的自相關函數，并且相對于其他寬帶平穩隨機信號來說，混沌序列的統計特性易于控制，較直接發射隨機信號更為方便。當混沌信號類型、參數和初始值確定的時候，完全可以復制產生，為己方的信號處理提供了便利。因此，考慮設計以混沌序列為基礎的正交波形集合。目前典型的混沌序列的產生可以通過選擇離散混沌系統的映射算法：如Logistic映射、Bernoulli映射、Tent映射、Chebyshev映射等；文獻[1-4]采用了Logistic映射，文獻[5]采用了Tent映射。由于離散系統參數少，產生機制簡單，所以在一定程度上設計自由度小，生成的數字信號難以在物理上與模擬信號對應。因此，為了方便信號實現，本文采用經典的Lorenz連續混沌系統[6]，提出基于Lorenz混沌序列調頻的正交波形集設計方法。

1 Lorenz混沌序列

Lorenz系統的數學模型為[7]：

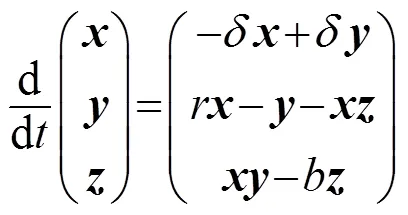
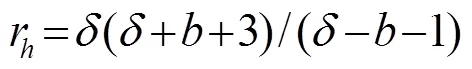
Lorenz系統產生混沌的必要條件為：

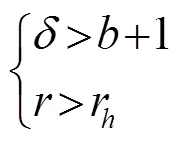
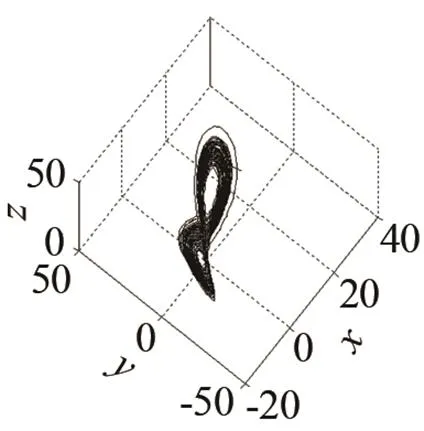
(a) 初值為[22, 8, 15]???? (b) 初值為[22.01, 8, 15]

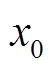
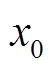
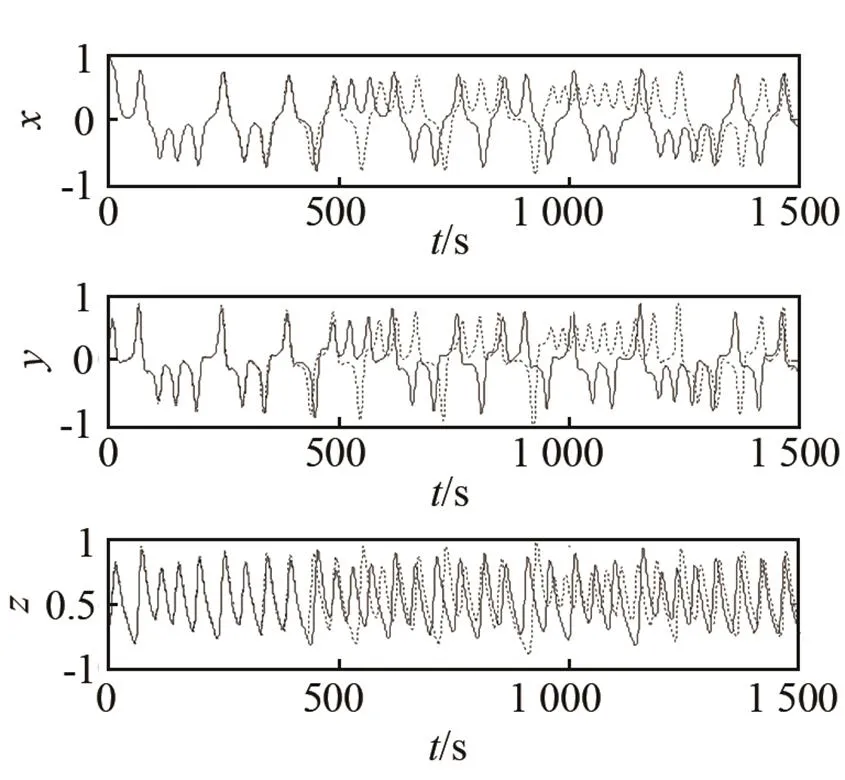
圖2 初值x0相差0.01時Lorenz序列各分量對比圖()

2 CFM正交波形集設計

2.1 CFM信號模型

一般頻率調制信號可以表示為[1]

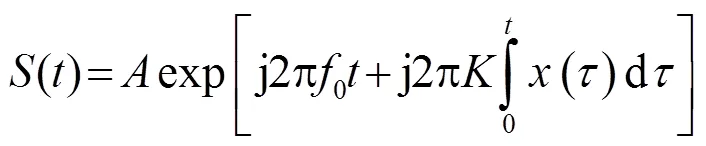
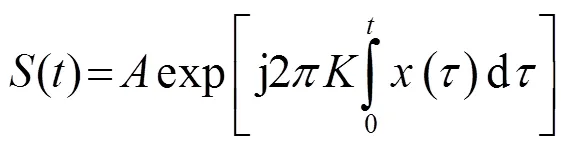
考慮到調頻信號的相關性能主要與其復包絡有關，因此，僅討論其復包絡部分，則式(5)的離散形式可表示為

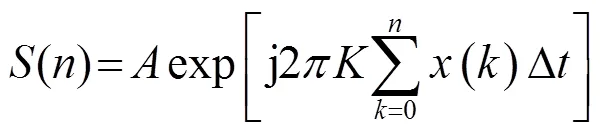
由式(4)可知，由于信號的瞬時頻率為[8]

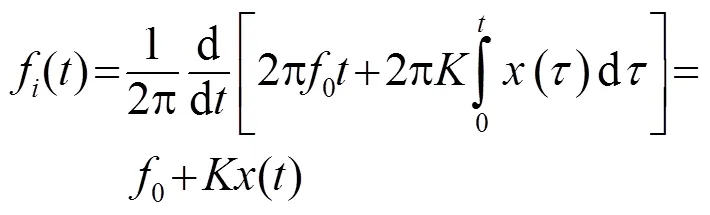
根據采樣定理，對基帶信號進行采樣，采樣頻率應滿足：

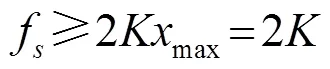
取采樣頻率為

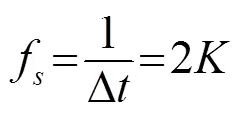
將式(9)代入式(6)，得到離散化CFM的復包絡為

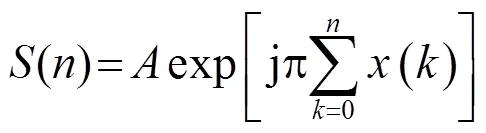
在得到混沌調頻信號模型后，任選幾個初值不同的Lorenz混沌序列，選取其分量，即可生成相應的CFM波形集，作為網絡水下航行器的發射波形。

2.2 CFM信號特性分析

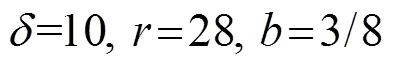
根據模糊度函數的定義[9]：

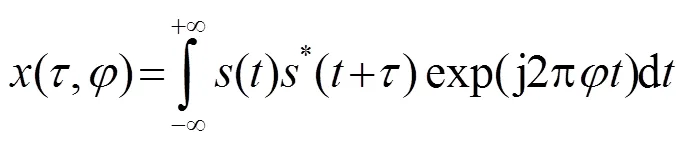
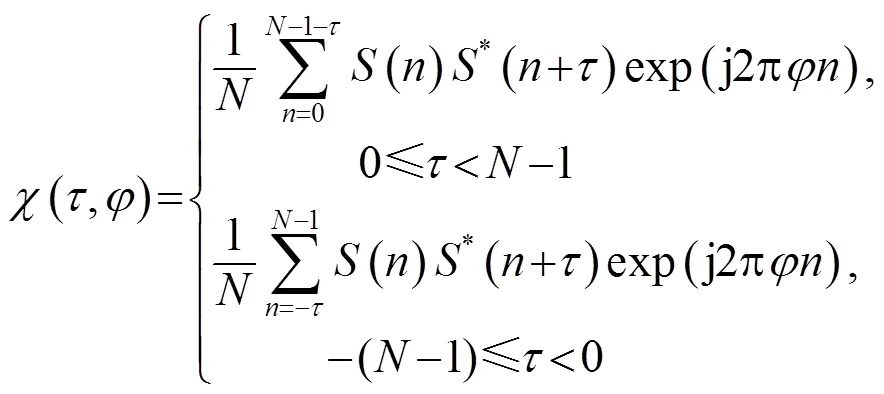
由式(12)可得，CFM信號的自相關函數為

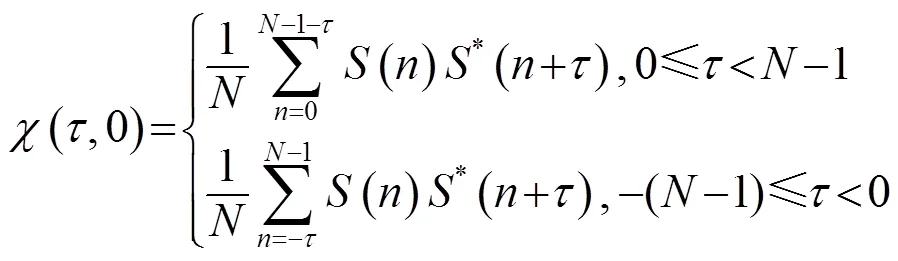
CFM信號的互相關函數為

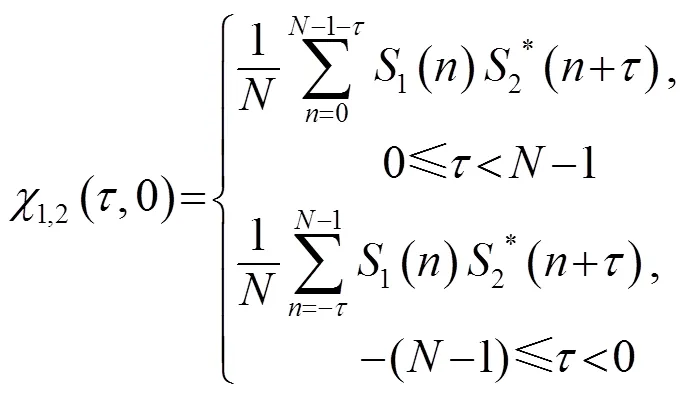
圖3、圖4中分別給出了基于Lorenz混沌序列的CFM信號的模糊度圖和自相關函數，可以看出，基于Lorenz混沌序列的CFM波形具有近似圖釘型的模糊度函數，自相關函數具有尖銳的主瓣和較低的旁瓣。因此基于Lorenz混沌序列的CFM信號具有較好的距離分辨力，是一種性能良好的脈沖壓縮信號。

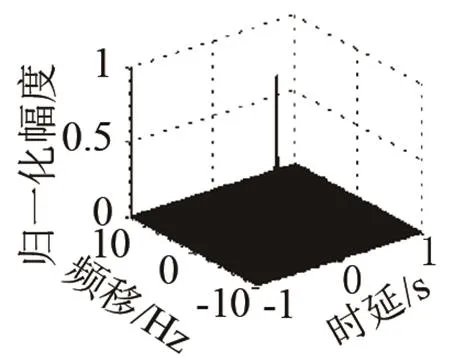
(a)1的模糊度圖 (b)2的模糊度圖

(c)3的模糊度圖

圖3 CFM信號1()、2()和3()的模糊度圖

Fig.3 Ambiguity diagrams of CFM signals:1(),2() and3()

(a) S1的自相關 (b) S2的自相關 (c) S3的自相關

圖 4 CFM信號S1(n)、S2(n)和S3(n)的自相關特性

Fig.4 Auto-correlations of CFM signals: S1(n), S2(n) and S3(n)

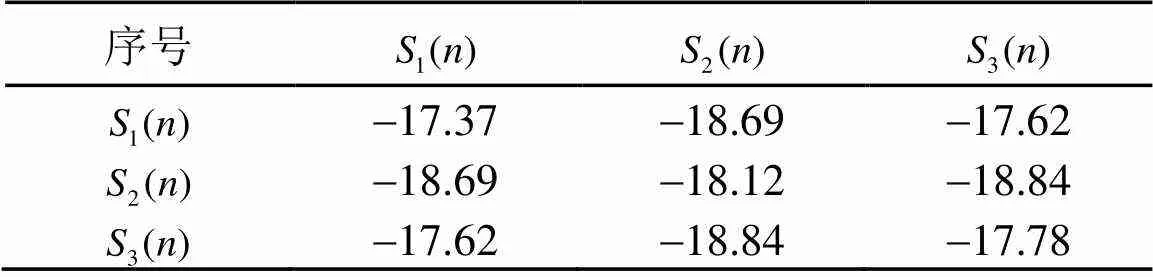
表1 自相關旁瓣峰值和互相關峰值(單位：dB)

(a) S1和S2的互相關(b) S1和S3的互相關(c) S2和S3的互相關

圖 5 CFM信號S1(n)、S2(n)和S3(n)的互相關特性

Fig.5 Cross-correlations of CFM signals: S1(n), S2(n) and S3(n)

2.3 CFM波形集個數和長度對波形集性能的影響分析

傳統的利用隨機尋優算法進行正交波形集設計時，正交波形集的性能會隨著波形集中波形個數的增加而下降，降低了波形設計效率[10]。圖6給出了波形個數與波形集性能(平均自相關旁瓣峰值和平均互相關峰值)之間的關系曲線。由圖6可以看出，波形集的性能沒有明顯變化，因此基于Lorenz序列的CFM正交波形集設計方法可以設計任意數目的波形集，不影響系統的性能，且設計時間不會增加，提高了波形集的設計效率。

圖7給出了波形長度與波形集性能(平均自相關旁瓣峰值和平均互相關峰值)之間的關系曲線，其中波形個數為3。由圖7可以看出，波形集的正交性能與波形長度有關，且長度越長，平均自相關旁瓣峰值和平均互相關峰值越低，波形集的正交性能越好。因此，在實際應用中，基于工程實踐可行性的基礎上，生成序列長度較大的波形集，以此保證波形集更好的正交性。

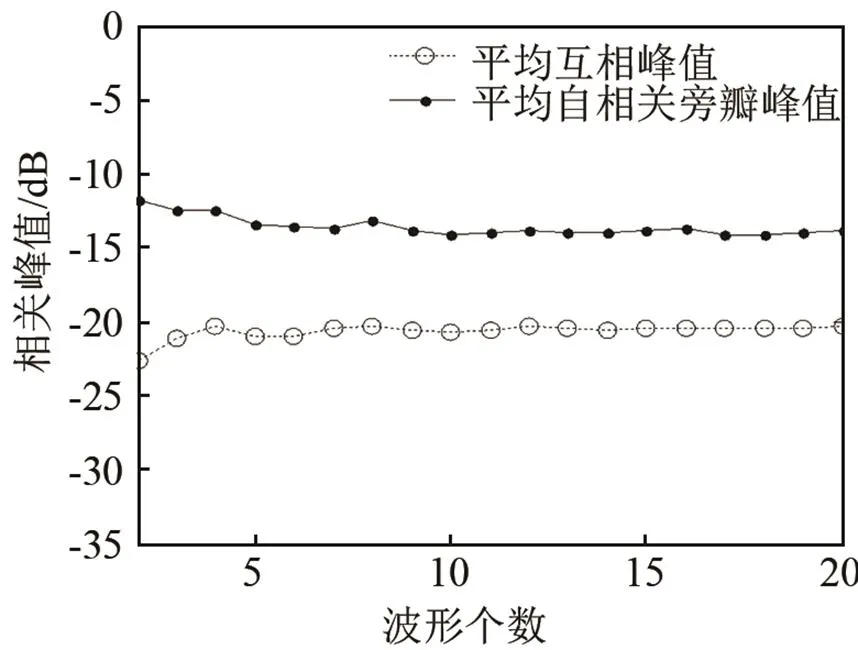
圖 6 波形集個數與波形集性能曲線

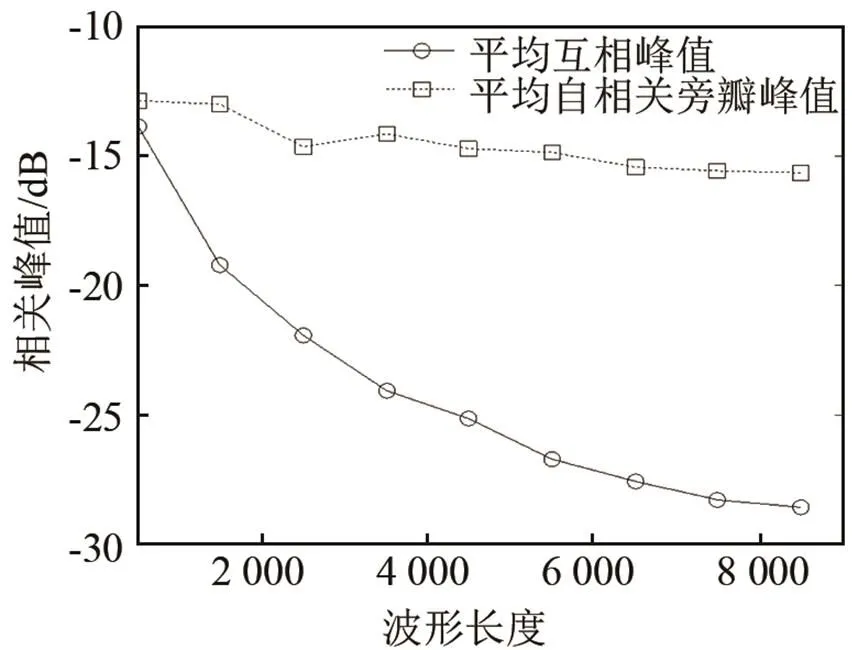
圖7 波形長度與波形集性能曲線

3 正交波形集的優化

利用混沌序列構成正交波形的方法簡單易行，可實時產生正交波形集。在此基礎上，還可從正交波形之間相關性的角度進行優化，進一步提高波形集的正交性能。本文中提出對混沌序列進行加Kaiser窗處理，然后采用混沌序列調制波形生成CFM信號，研究波形集之間的相關性能。

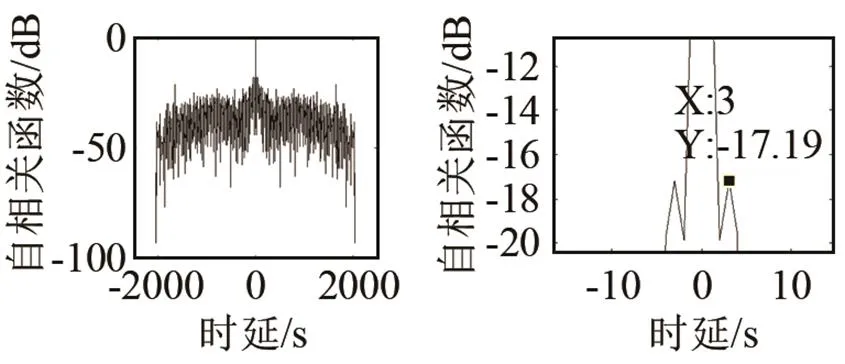
(a) 加Kaiser窗前?? (b) 圖(a)的局部放大圖

(c) 加Kaiser窗后?? (d) 圖(c)的局部放大圖

圖8 加Kaiser窗前后的CFM自相關函數對比

Fig.8 Auto-correlations of CFM signals with and without adding Kaiser window

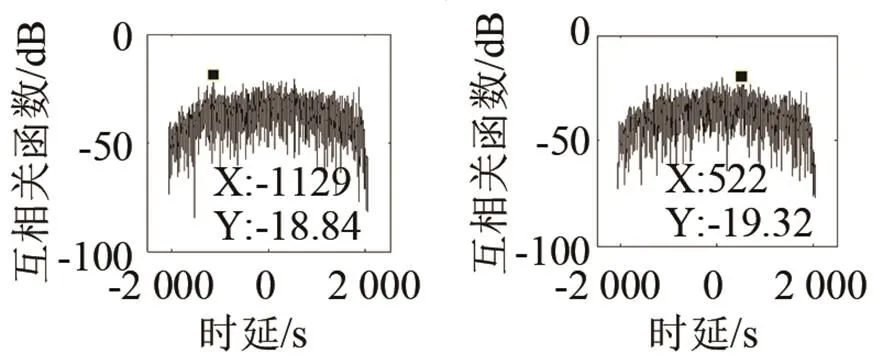
(a) 加Kaiser窗前?? (b) 加Kaiser窗后

4 CFM信號的檢測性能研究

圖10給出了網絡水下航行器多節點探測的模型，假設有3個探測器，分別發射信號1、2、3，由于回波信號間的串擾，對于每個探測器的接收機來說，都可以接收到三個發射信號經過目標反射后的回波。本文主要對比分析了當探測器分別發射CFM信號和LFM信號時，探測器對于本機接收到的回波信號的處理以及后續的檢測性能，觀察探測器能否正確識別本機所發射的信號對應的回波并進行后續的信號檢測與處理，以此說明將CFM作為發射信號時的優勢。圖11給出了正交混沌波形集檢測框圖[2]，圖中CFM正交波形由發射端發出后，目標回波在接收時進行自相關、互相關匹配濾波，接收端信號則與發射端一一對應，避免信號波形相互干擾。

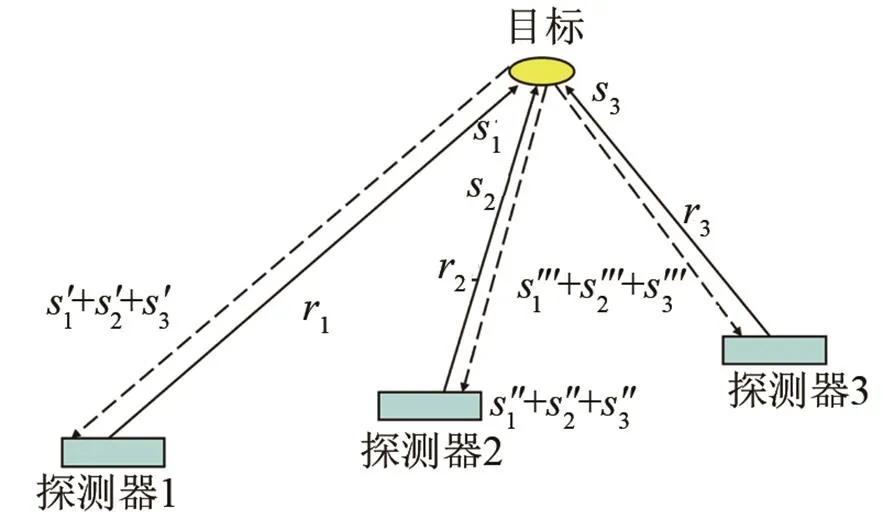
圖10 探測器發射信號、接收回波模型

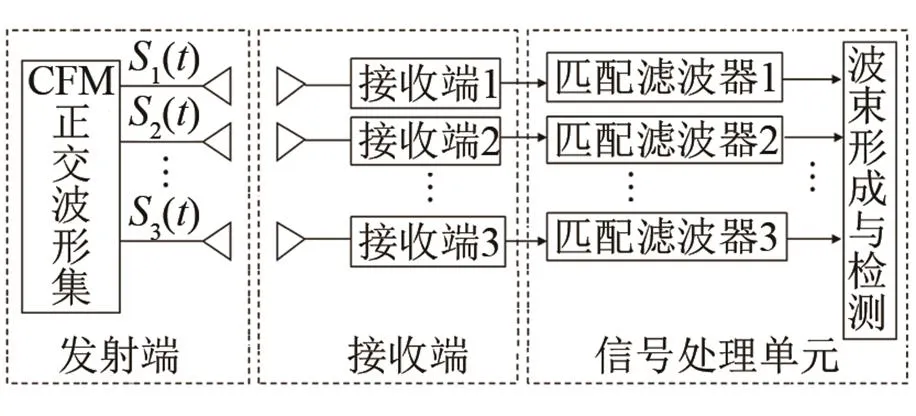
圖11 正交混沌波形集檢測框圖

圖12(a)、12(b)分別給出了發射CFM信號時探測器1、探測器2、探測器3接收到的回波信號和經過匹配濾波器處理后的輸出結果。圖13(a)、圖13(b)分別給出了發射LFM信號時探測器1、探測器2、探測器3接收到的回波信號和經過匹配濾波器處理后的輸出結果。可以看出，相對于LFM信號，將CFM信號作為發射信號時，由于CFM波形集的正交性，對回波作匹配濾波處理的過程中有效克服了回波信號間的串擾，信號處理器對目標的檢測性能更好。

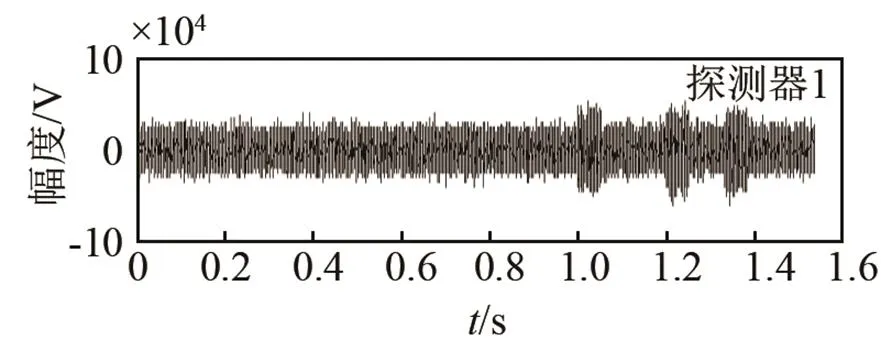
(a) 探測器接收到的回波信號

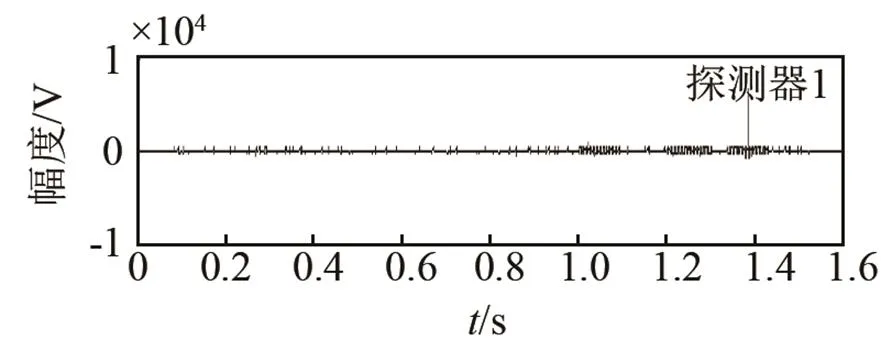
(b) 匹配濾波器的輸出

圖12 發射CFM信號時的回波檢測性能

Fig.12 Echo detection performance for transmitting CFM signals

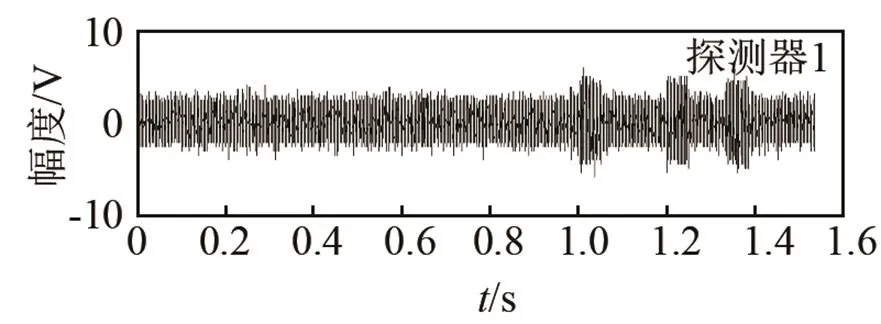
(a) 探測器接收到的回波信號

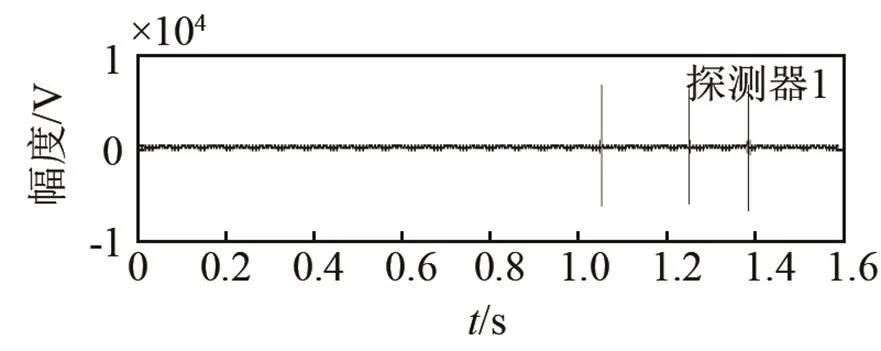
(b) 匹配濾波器的輸出

圖13 發射LFM信號時的回波檢測性能

Fig.13 Echo detection performance for transmitting LFM signals

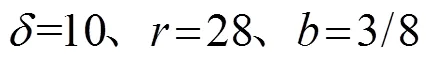
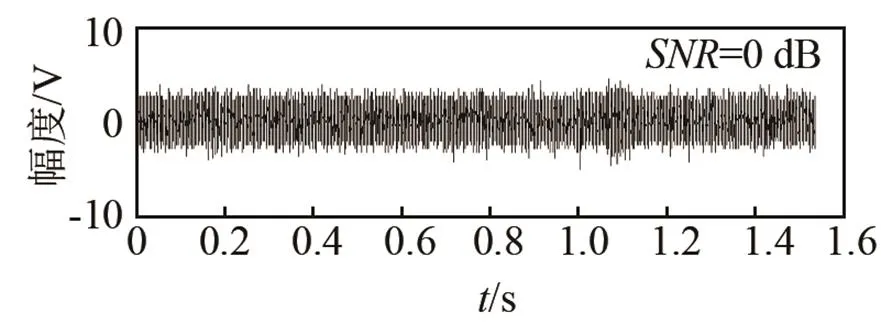
(a) 低信噪比條件下的回波信號

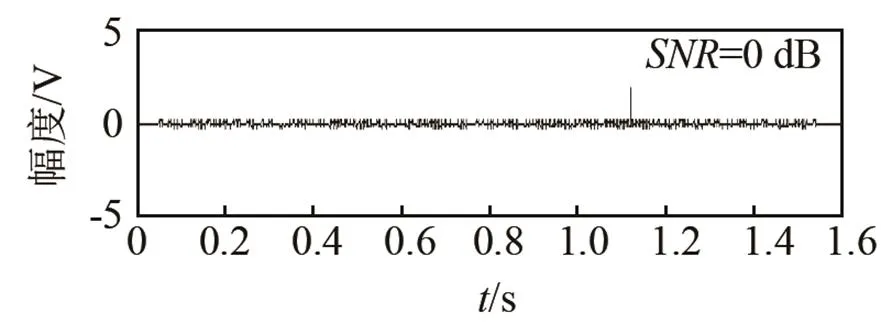
(b) 匹配濾波器的輸出

圖14 低信噪比條件下CFM回波檢測性能

Fig.14 CFM Echo detection performance under low signal to noise ratio

5 結論

通過理論分析和計算機仿真可以看出，基于混沌序列的CFM正交波形集的設計方法是簡便可行的。文中給出了基于Lorenz混沌序列的正交波形集的設計及特性研究，并提出了正交波形集的優化方法。最后，研究了CFM信號相對于常規LFM信號在檢測方面的優勢。仿真結果表明，利用Lorenz混沌系統產生的混沌序列能設計任意波形個數的正交波形集，設計靈活多變，算法簡便高效。

[1] 牛朝陽, 李曉波. MIMO雷達正交混沌調頻波形集設計[J]. 信號處理, 2013, 29(3): 394-399. NIU Zhaoyang, LI Xiaobo. Design of orthogonal waveforms set for mimo radar based on chaos frequency modulation[J]. Signal Processing, 2013, 29(3): 394-399．

[2] 牛朝陽, 張劍云. 混沌序列的MIMO雷達正交波形集設計[J]. 火力與指揮控制, 2012, 37(8): 151-154. NIU Zhaoyang, ZHANG Jianyun. Design of orthogonal waveforms set for mimo radar based on chaotic sequence[J]. Fire Control & Command Control, 2012, 37(8): 151-154,

[3] 孫明亮. 基于混沌信號的MIMO雷達波形設計方法研究[D]. 長春: 吉林大學, 2014:24-26. SUN Mingliang. Research on methods of MIMO radar waveform design based on chaotic signals[D]. Changchun: University of Jilin, 2014:24-26.

[4] 王佳佳, 謝亞楠, 譚子苗. 混沌調頻-調相MIMO雷達正交波形設計[J]. 應用科學學報, 2014, 32(6): 588-595．WANG Jiajia, XIE Yanan, TAN Zimiao. Frequency-modulated and phase-modulated orthogonal waveform design for MIMO radar based on chaotic map[J]. APPLIED SCIENCE-Electronics and Information Engineering, 2014, 32(6): 588-595.

[5] 周云, 盧霞霞, 于雪蓮, 等. 基于混沌的調頻調相的多輸入多輸出雷達正交波形設計[J]. 計算機應用, 2015, 35(12): 3357-3361. ZHOU Yun, LU Xiaxia, YU Xuelian, et al. Multiple input multiple output radar orthogonal waveform design of joint frequency-phase modulation based on chaos[J]. Computer Applications, 2015, 35(12): 3357-3361．

[6] Lorenz E N. Deterministic non-periodic ?ow[J]. Journal of the Atmospheric Sciences, 1963, 20(2): 130-141.

[7] 陳玉明. 基于Lorenz型系統的四維超混沌系統的復雜動力學研究[D]. 廣州: 華南理工大學, 2014: 19-20.CHEN Yuming. Research on complex dynamics of four- dimensiona hyperchaotic systems based on Lorenz-type systems [D]. Guangzhou：South China University of Technology, 2014: 19-20.

[8] 李志舜. 魚雷自導信號與信息處理[M]. 西安: 西北工業大學出版社, 2004: 143-144. LI Zhishun. Signal and Information processing of ho-ming torpedo[M]. Xi'an: Northwestern Polytechnical University Press, 2004: 143-144.

[9] 朱埜. 主動聲吶檢測信息原理[M]. 北京: 科學出版社, 2014: 76-77. ZHU Ye. Active sonar detection information theory[M]. Beijing: Science Press, 2014: 76-77.

[10] 劉波. MIMO雷達正交波形設計及信號處理研究[D]. 成都: 電子科技大學, 2007: 67-68. LIU Bo. Research on generation of orthogonal waveform and signal processing for MIMO radar[D]. Chengdu: University of Electronic Science and Technology, 2007: 67-68.

Design of underwater orthogonal waveforms set based on Lorenz chaos frequency modulation

TIAN Jing1, CHEN Hang1,2, TANG Jing-zhi1, TENG Duo1,2

(1. School of Marine Engineering, Northwestern Polytechnical University, Xi'an 710072, Shaanxi, China;2. National key Lab of Underwater Information Processing and Control, Xi'an 710072, Shaanxi, China)

A method based on Lorenz chaos frequency modulation is proposed to design orthogonal waveform sets for the joint detection of the network underwater vehicles where the interferences may existbetween echo signals.First, the CFM (chaos frequency modulation) signal model based on Lorenz sequence is established, and its correlation properties and orthogonal performance are analyzed, including the effectsof the number and the length of waveforms on the orthogonal performance. The optimization method of the CFM orthogonal waveforms by adding window function to the chaotic sequence is proposed. And then, the echo signal model based on the network group of underwater vehicle that transmits linear frequency modulation signal and CFM signal is structured, and the processing results of the echo signals by using matched filter are compared and analyzed. The simulation results indicate that the method is simple, flexible and efficient, producing a set of orthogonal waveforms with good performances, which has obvious advantage in underwater information detection.

chaos sequence; frequency modulation; orthogonal waveforms; network underwater vehicle

TN911.7

A

1000-3630(2017)-02-0116-07

10.16300/j.cnki.1000-3630.2017.02.004

2016-07-26;

2016-10-20

水下信息處理與控制國家重點實驗室基金資助項目(9140C230304140C23001)

田晶(1992－), 女, 陜西渭南人, 碩士研究生, 研究方向為水下信號與信息處理。

田晶, E-mail: 15339297372@163.com