冷鏈多配送中心配送路徑優化研究

梁承姬　楊繼滔　黃濤

[提要] 為解決在冷鏈多配送中心的貨物調配過程中配送中心缺貨和運輸成本高的問題，提出通過其他配送中心協助完成貨物的調配，即橫向轉運策略，建立配送成本最小和顧客滿意度最大的多目標數學模型。由于生鮮產品具有易腐的特性，引入懲罰函數處理約束，并對遺傳算法改進。在求解中，由于配送范圍內客戶點多，先采用重心分區法對客戶點進行分區，使得每個配送中心負責一定區域的客戶點，再通過改進遺傳算法優化分析帶模糊時間窗冷鏈物流問題和多配送中心貨物調配問題。最后，由算例分析，可以看出所建模型和采用的算法能夠縮短路徑，降低配送成本。

關鍵詞：橫向轉運；重心分區法；改進遺傳算法；顧客滿意度

基金項目：國家自然基金資助（71471110、61540045）；上海市科委創新項目資助（14170501500、14D2280200工程中心、16DZ1201402、16040501500）；上海市重點學科資助（J50604）；陜西省社會科學基金資助項目（2015D060）

中圖分類號：TP202+.7 文獻標識碼：A

收錄日期：2017年9月6日

冷鏈物流配送在國外的研究由來已久，發展更是早于國內，對冷鏈配送和車輛路徑問題的分析也較成熟完善，提出了多配送中心車輛調度的問題，即MDVRP。根據現實情況需同時考慮送貨和取貨，建立了帶時間窗的車輛配送問題。多配送節點的車輛路徑問題模型特點，給出合適的自適應的遺傳算法。王科峰、葉春明將節點單需求和節點雙重需求模型進行了對比分析，說明了啟發式算法的改良對成本節省的實際效果。李華考慮的是約束條件未知下考慮送取貨的多目標車輛路徑問題。Karl F.Doerner研究了帶有時間窗的送貨和取貨同時考慮的車輛路徑問題。NabilaAzi在解決容易腐爛的食品配送的VRP優化問題上使用了距離路程最短法。于坤根據傳統典型的送貨和取貨同時考慮的車輛路徑問題為基礎，構建基于該問題的城市冷鏈物流配送路徑優化模型。結合模型設計遺傳算法求解其具體配送方案。陳沖就生鮮農產品的車輛配送問題進行了研究，基于軟時間窗約束條件，考慮產品的貨損周期，采用節約法對模型求解和分析。如果物流網絡采用庫存集中管理模式，還需要考慮集中庫存的再分配問題。橫向轉運可實現配送中心之間的物資再分配。橫向轉運是物料在同一層級的設施間定向運動達到補充庫存的目的。例如，從供應商到制造商，從制造商到分銷商，層間流動的方向和物流比較容易確定。相比之下，橫向轉運是更為靈活的庫存補充再分配方式。

本文結合當前配送路徑的研究以及對橫向轉運的概述，考慮到冷鏈物流承載的貨物具有一定的特殊性且對溫度的要求較高，提出在冷鏈物流配送中設定模糊時間窗來反映顧客滿意度。同時，探討了多配送中心的冷鏈物流存在的某一配送中心無法滿足某一需求點的貨物調配問題，在該問題的研究中，以配送點至客戶點、配送點之間的成本和顧客滿意指標來設立多目標模型。為優化多配送中心的配送路徑，在求解中，先采用重心分區法對客戶點進行分區，使得每個配送中心負責一定區域的客戶點，再通過改進遺傳算法優化分析帶模糊時間窗冷鏈物流問題和多配送中心貨物調配問題。由算例分析可以看出所建模型和采用算法的研究意義。

一、問題描述

由于當前城市規模不斷擴大，消費者對物流配送的需求明顯升高。從物流配送方面考慮，客戶點呈現逐年增多、區位復雜的特點，通過對客戶點分區，設立多配送中心進行物流配送，可以避免配送車輛線路雜亂、時間長、成本高的缺點。同時，隨著電子商務量和人們生活水平的提高，物流配送需求越來越大，配送中心的供貨壓力也較以往增大。在現實生活中，配送中心往往存在庫存不足、客戶點需求增加等情況，通過考慮配送中心的貨物調配，對多個配送中心的貨物需求進行實時監測，及時補貨可以減少對相應客戶點的配送時間，降低成本。

本文考慮的基于多配送中心貨物調配的冷鏈運輸優化問題，即在一定區域范圍內，有若干需要配送的客戶點和多個配送中心，且配送中心有確定的配送范圍。在配送中心發車向該配送范圍內的客戶點配送冷鏈貨物的過程中，車輛需要在約定好的時間約束范圍內完成配送，不符合實際約束就會有不同程度的懲罰成本。每個配送中心的庫存是固定的，在分區后，由于個別配送點的配送壓力增加或需求變化，會出現配送中心A庫存不足或者客戶點需求增加的情況，導致無法完成對某個客戶點a配送的情況，此時將進行判斷并進行選擇：（1）鄰近的配送中心B完成該區域配送后再對客戶點a進行配送，然后返回配送中心B；（2）配送中心B補貨給配送中心A，配送中心A再對客戶點a所屬路線進行配送。選擇時間成本、距離成本較小的方案進行配送。該方法可以針對庫存不足或需求增大做出相應合理的配送方案，從時間、貨物質量等方面考慮都得到了明顯改善。關于整個流程的車輛配送時序圖，如圖1所示。（圖1）

二、模型建立

（一）基本假設。（1）各個客戶需求點位置和需求已知，各負責倉儲配送點的位置已知；（2）所有有需求點客戶點的配送任務都要完成，并且只能通過一輛配送車對每個配送路徑上的點服務；（3）配送車從倉儲配送點出發開始服務，完成后返回出發點；（4）配送中所有的運輸距離都滿足小于配送運輸車輛的行駛距離約束要求；（5）配送中心需要補貨由其他配送中心進行調配，車輛在完成補貨后返回發車配送中心。

（二）參數定義。k：配送的車輛總數，v∈k；M：配送中心點，m∈M；n：接受配送的客戶點；fm：配送中心m配送貨物的冷鏈成本；a：配送車輛單位距離成本；b：配送車輛單位空載成本；pi：客戶點i需求貨物的價值；？著：冷鏈貨物的貨損率，？著=1-e-？茁；qm：配送中心m對冷鏈貨物的需求補貨量；dij：配送中心i為配送中心j貨物調配距離；S■■：車輛v到達客戶點i的時間。

（三）決策變量。S■■：配送中心m的車輛到客戶點i的時間；h■■：當配送中心i負責配送中心j的貨物，調配為1，否則為0；r■■：當配送中心i調配車輛m至配送中心j為1，否則為0；x■■：當車輛v由配送中心m從客戶點i配貨至客戶點j時，為1；否則為0；y■■：客戶點i由配送中心m配送為1，否則為0；A■■：等于最佳服務時間下限ei減去到達時間S■■；D■■：等于到達時間S■■減去最佳服務時間上限li。endprint

（四）目標函數及約束條件

目標函數：

MinLP1=■■■■x■■（f■+ad■）+■■■ah■■d■+r■■+f■ （1）

MinLP=-■ （2）

約束條件：

f■=■y■■p■？著+■■？姿A■■+？姿D■■ （3）

■■y■■=n （4）

■■■x■■=n （5）

■■q■x■■+q■h■■≤Q （6）

■■■x■■+h■■≤■ （7）

■x■■=■x■■？坌m∈Mv∈k （8）

A■■≥e■+l■ （9）

D■■≥S■■-l■ （10）

A■■≥0，D■■≥0 i∈n，v∈k （11）

x■■∈{0，1} ？坌i∈n，j∈n，v∈k，m∈M （12）

h■■∈{0，1} ？坌i∈n，j∈n，m∈M （13）

y■■∈{0，1} ？坌i∈n，m∈M （14）

本文建立的是基于模糊時間約束的多目標冷鏈運輸路徑優化模型。模糊時間窗的設立表示車輛應盡量在顧客要求的時間窗內服務，但不同于對固定時間窗的硬性要求，對大多數非剛性需求時要求服務時間外也可以進行服務，以部分成本作為懲罰，同時將車輛服務時間用顧客對服務的滿意程度來表達，更加直觀全面的描述分析需求。車輛對客戶點配送的不同情況如圖2所示，每個客戶點都有一個最優服務時間[ei，li），在此服務時間內沒有時間懲罰成本且顧客滿意度最高，同時在模糊時間窗[ei'，ei）和[li，li'）內會產生時間懲罰成本且影響顧客滿意度，模糊時間窗之外的任何時間，客戶點將拒絕接受服務，需要車輛等待至模糊時間窗內或者重新服務，最后每個顧客的服務結束后回到原配送地。（圖2）

本文對模糊時間窗分析設定如下：

G（Siv）=0 Siv∈[0，ei'）■ Siv∈[ei'，ei）1 Siv∈[ei，li）■ Siv∈[li，li'）0 Siv∈[li'，∞） （15）

在該公式中，車輛進行配送的時間被分層五部分。在[0，ei'）和[li'，∞）區間內，客戶對配送服務的滿意度為0，拒絕接受服務；在[ei，li]區間內，客戶對配送服務最滿意，此時不需要考慮懲罰產生的額外成本；在[ei'，ei]和[li，li']內，車輛也可以對顧客進行配送，但需支付一定的懲罰成本，同時顧客滿意度隨Siv的具體時間來確定，需要注意的是，由于延遲服務所耗的時間更久，且顧客更不希望等待車輛服務，所以設定延遲服務額外成本大于時間窗服務的額外成本。

上述模型的目標函數為兩個：一是降低冷鏈運輸中的成本；二是提高顧客對配送服務的滿意程度。式（1）表示降低冷鏈運輸中的成本，由兩部分組成：一是配送中心向各個客戶點配送的成本，包括冷鏈成本和距離成本；二是配送中心間的貨物調配產生的成本，包括距離和空載成本、貨損成本、懲罰成本；式（2）表示建立求解顧客對配送服務的滿意程度最大化目標函數；式（3）表示車輛在向客戶點配送貨物時產生的冷鏈成本，包括貨損成本和時間窗懲罰成本；式（4）表示一個配送中心負責一個需要配送的客戶點；式（5）表示所有有需求點客戶點的配送任務都要完成；式（6）表示冷鏈配送和貨物調配的需求都不會大于車輛總載重；式（7）表示配送和貨物調配所需的車輛不大于總車輛；式（8）表示冷鏈運輸車輛從配送中心出發點發車，經過一個或多個客戶點后返回發車的起點；式（9）表示當車輛提前于已知確定的時間窗約束到達，計算出的提早服務時間；式（10）表示若車輛晚于已知確定的時間窗約束到達，計算出的延遲服務時間；式（11）表示提早服務時間和延遲服務時間是非負的，即保證模糊時間窗存在；式（12）、（13）、（14）表示使決策變量值為0或1的整數限制式。

三、算法求解

（一）多邊形重心分區法。本文采用多邊形重心分區法，充分考慮了多配送中心的情況，先連接所有配送中心的坐標點，形成一個封閉的多邊形，通過計算求得其重心坐標，再將中心坐標與多邊形的每條邊的中點相連并向外形成射線而把配送范圍分成一個個不同的配送區域。每個區域各自有對應的配送中心，負責該區域的配送服務，不同范圍的配送任務不干擾、不交叉。（圖3）

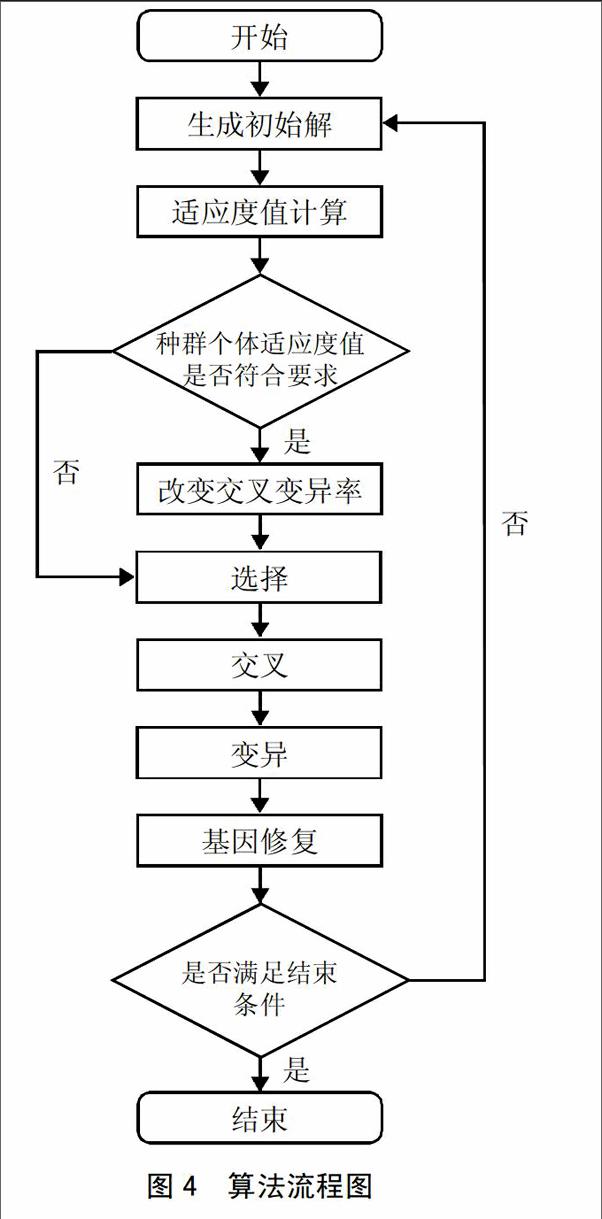
（二）遺傳算法求解。在本章節對車輛路徑優化求解中，第一階段將若干客戶點進行了合理的分區，在第二階段，本文采用遺傳算法對具體的配送中心為客戶點運輸服務的路徑問題以及配送中心貨物調配的問題進行優化求解。通過在算法操作中，對個體適應度值的判斷，不斷改變交叉率和變異率，并且在操作結束后進行基因修復，可以有效防止早熟現象的發生，避免操作后的染色體不符合約束，確保算法求解的穩定性。如圖3所示整個算法的流程圖，在確定個體適應度值后，做出相應判斷，如果趨于一致則增加pc和pm概率。若較為分散，就減小pc和pm概率。在選擇交叉后的基因修復可以有效地防止染色體不符合約束條件，確保算法求解的穩定性。（圖4）

1、染色體編碼。假定有m個配送中心為n個客戶點進行運輸。染色體第一部分為每個配送點發出車輛1，依次遍歷相應客戶需求點，然后返回配送起點的路徑。現有3個配送點和25個客戶需求點，假設染色體第一部分的編碼設計為12-9-21-3-14-23-5-19，該染色體編碼就是一個可行的運輸方案。首先通過分區，確定每個配送中心要為哪些客戶點運輸服務。配送中心1的第1輛車m11負責的客戶點分別是12、9、21，配送中心1的第2輛車m12負責的客戶點分別是3、14、23、5、19，則該染色體是已分配好客戶點的配送中心1的配送方案，通過解碼可以得出屬于該染色體編碼的具體方案為：m11-12-9-21-m11m12-3-14-23-5-19-m12。同理，根據該操作可以得到關于配送中心2和配送中心3配送方案的染色體編碼。整體的染色體編碼如：12-9-21-3-14-23-5-19-0-18-10-2-13-24-7-1-20-0-17-25-6-15-8-16-22-4-11。endprint

2、生成初始種群。本章算法設計中，通過隨機生成若干染色體來構造初始種群。任意取n個基因數（n=客戶點數量），將這n個基因數隨機設定在不同的染色體基因位中，這樣就生成了冷鏈運輸路徑的服務方案。

3、交叉算子。本文所進行的交叉算子操作如圖所示，首先，從父代1里任意選取3個基因位上的基因值，將其復制到子代相同基因位上；然后去掉父代2中與父代1所選基因值相同的基因；最后子代1中的基因位值由父代2里仍保留的基因有序填充，如果遇到某一基因位上已經存在基因值，則跳過該基因位繼續填入下一個位置。本章選取的交叉操作方法如圖5所示。（圖5）

4、變異算子。在遺傳操作中，變異算子遵循一定的變異概率，模仿生物學中基因突變原理，為了開拓染色體不同組合的多樣性，從而進行染色體變異。如圖5，這里選取父代中的兩個隨機基因，進行調換，從而達到變異的效果，產生新的子代。（圖6）

5、適應度函數。作為遺傳算法衡量染色體個體的優劣準則，適應度函數充分結合了問題本身的要求和考慮約束，一般與目標函數需要緊密相連，才能作為判斷標準的主要依據。本文綜合考慮將目標函數作為適應度函數。即Fi=minLP1-100·n（minLP2）的形式。其中，目標函數LP2是0～1內的小數，代表客戶對服務的滿意程度，對適應度函數的影響程度較小，所以選擇100作為變換因素，將顧客滿意度轉化為費用。

6、基因修復。本文考慮的是基于配送中心貨物調配的冷鏈車輛路徑問題，在交叉和變異操作后，會由于條件和約束限制，染色體會出現不符合規則的情況。故針對不符合條件的染色體進行如下步驟的基因修復：

第1步：判斷交叉變異后的染色體中，所有配送中心每輛車配送的客戶點是否大于等于2，如果是轉入第二步，如果不是則放棄該染色體重新生成，再次判定。

第2步：由于染色體中含有沒有意義的數字為0的基因位，所以判斷在交叉變異后是否存在間隔符0相鄰的情況，這種情況會導致有車輛閑置，配送中心無配送任務，若不是轉為下一步，若是則隨機選取其他基因位隨機段插入兩個間隔符0之間。

第3步：判斷染色體中包含間隔符0的數量是否等于3，等于則符合條件，不等于會生成少于3個配送中心的配送方案，任意選取兩個基因位間插入一個間隔符0，使染色體符合條件限定。

四、算例分析

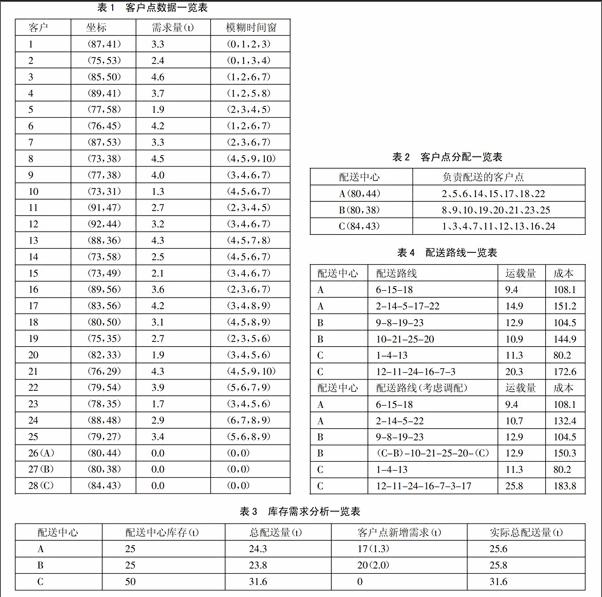
（一）算例介紹。假設配送中心數量為3個，有25個需要運輸服務配送的客戶點，客戶點經過分區已確定由哪個配送中心配送。車輛每公里運輸成本為2元，冷鏈中的貨損率為7%，冷鏈貨物的價格為1，500元/t，？姿1=0.5，？姿2=1.0，？茁=1.0。本章節模糊時間窗ei'，ei，li，li'。ei，li是指顧客對運輸服務滿意度為1的時間窗，把該時間窗各項兩端擴展1h，即ei'=max{0，ei-1}，li'=li+1。在25個客戶點后，標號為26、27、28的分別代表3個配送中心A、B、C，庫存量分別是25、25、50。具體初始數據如表1所示。（表1）

通過分區，得出各個配送中心負責的客戶點，具體如表2所示。（表2）

在實際配送算例中，部分客戶點因市場原因會出現需求增長，如表3所示，屬于配送中心A的客戶點17新增了1.3t的需求量，屬于配送中心B的客戶點20新增了2.0t的需求量，這也使得實際總配送量發生改變，對比配送中心的庫存量，則需要進行貨物調配才能完成每個客戶點的配送。（表3）

對于算法中相應的參數設置為：N=100，迭代數為200，pc=0.8，pm=0.05。通過Matlab運行求解。

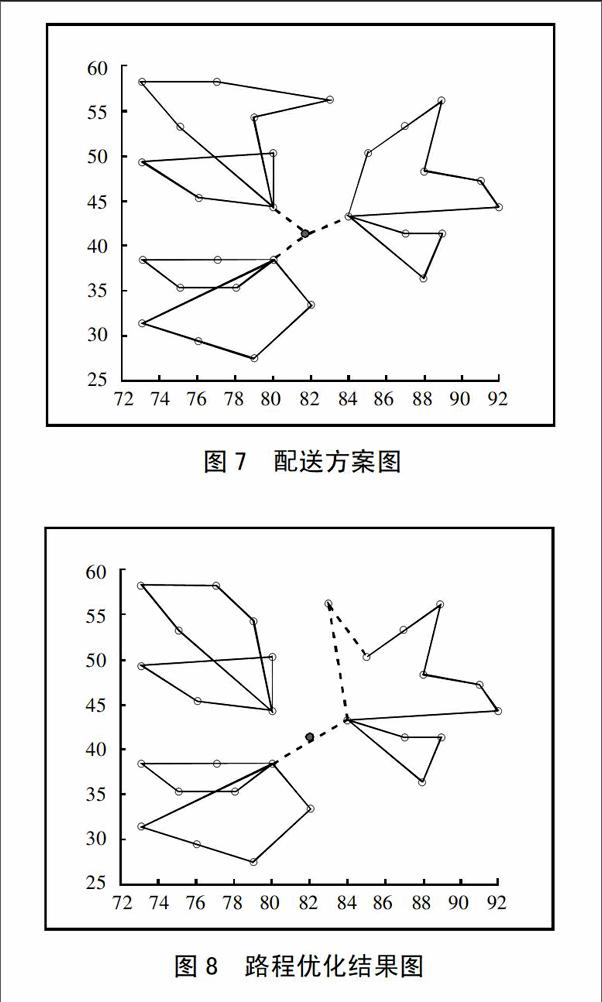
（二）不考慮調配的優化方案。首先得出一個不考慮客戶點需求增加，不需要貨物調配的配送方案，如圖7所示。（圖7）

在圖7所示的配送方案中，選取一個距離3個配送中心距離接近的點作為一個虛擬發貨點，這樣由虛擬發貨點向3個配送中心延伸，再進行路徑優化。虛擬發貨點延伸的路程成本不算在總成本內。由于事先進行的分區操作，使得整個區域的客戶點配送路徑更加合理清晰。

（三）考慮橫向轉運的優化方案。在考慮客戶點需求增加后，發現負責A配送的客戶點17和負責B配送的客戶點20出現需求變動，兩個配送中心皆不能完成對相應需求變動的客戶點的配送，因此需要由庫存充足的配送中心C進行貨物調配。為了保證符合目標函數成本最小的條件，在確定貨物調配之前需要對不同的方案進行對比判定。

方案1：C在完成負責區域的配送后，繼續為客戶點17配送貨物再返回C。

方案2：C將貨物配送至A，貨物調配車輛再返回C，仍由A為客戶點17進行配送。

新增的貨物需求導致配送中心無法按原計劃進行配送，確定新的配送方案需要根據不同路線距離成本的對比來決定如何選擇。通過對圖7的配送結果圖中可以分析出，方案1因配送客戶點17，需要走的路徑為3-17-C，再減去原本3-C的距離，同時省去了配送中心C中5-17-22的路程；方案2需要走的路徑為C-A-C，其他路徑不變。可由距離計算公式d=■得出距離的對比結果。客戶點20的判斷方法同理。（圖8）

圖8是判斷配送方案后的優化結果，客戶點17由配送中心C的分支路線配送，在配送中心C將貨物運送至B后，客戶點20仍由配送中心B進行配送，優化后的配送方案具體配送路線和成本對比如表4所示。（表4）

五、小結

為了解決在冷鏈多配送中心的貨物調配過程中，配送中心缺貨和運輸高成本問題，提出通過其他配送中心協助完成貨物的調配，即橫向轉運策略，建立配送成本最小和顧客滿意度最大的多目標數學模型。由于生鮮產品具有易腐的特性，引入懲罰函數處理約束，并對遺傳算法改進。

本文中在不考慮客戶點需求變化之前的總運載量為79.7t，總成本為761.5。加入需求變化考慮因素，客戶點17和客戶點20分別增加需求1.3t和2.0t，同時判斷配送路線成本，在優化后選擇的配送路線總運載量為83t，總成本為759.3。可以看出，在總運載量提高的前提下，通過路線優化，成本反而得以下降。

主要參考文獻：

[1]Laura Calvet，Albert Ferrer，M.Isabel Gomes，Angel A.Juan，David Masip.Combining statistical learning with metaheuristics for the Multi-Depot Vehicle Routing Problem with market segmentation[J].Computers & Industrial Engineering，2016.8.

[2]Chao Wang，Dong Mu，Fu Zhao，John W.Sutherland.A parallel simulated annealing method for the vehicle routing problem with simultaneous pickup delivery and time windows[J].Computational Optimization and Applications，2015.4.83.

[3]鄭翀.基于自適應遺傳算法的多配送中心車輛調度優化[D].遼寧：大連海事大學，2013.

[4]王科峰，葉春明.節點具有雙重需求車輛路徑問題及其解的性質分析[J].上海理工大學學報，2013.35.4.

[5]李華.具有同時配送和回收需求的車輛路徑問題研究[D].四川：西南交通大學，2007.

[6]李宏.城市冷鏈物流配送車輛路徑問題的研究[D].湖南：長沙理工大學，2006.

[7]Herer，Y.T，Tzur，M，Yucesan，E.The multil-ocation transshipment problem[J].IIE Trans-action，2006.38.endprint