隨機中斷和隨機需求下閉環供應鏈最優回收定價模型
權蓉 顏榮芳


摘要討論了由一個制造商、一個零售商和一個第三方回收商組成的閉環供應鏈的差別定價問題.基于博弈論的理論和方法在集中式和分散式決策情形下分別建立了第三方回收定價模型,并給出了隨機中斷和隨機需求下閉環供應鏈的最優定價策略組合,最后通過數值例子分析了供應中斷對最優批發價和零售價的影響.
關鍵詞物流與供應鏈管理;隨機中斷;博弈論;差別定價
中圖分類號F270.7文獻標識碼A
Optimal Collection Pricing Model for ClosedLoop Supply Chain under Stochastic Disruption and Stochastic Demand
Rong QUAN,Rongfang YAN
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou,730070,China)
AbstractThis paper discussed the problem of the differential pricing of closedloop supply chain consist of one manufacturer,one retailer and a third party recycler.Based on the theory and method of game theory,we established the third party collection pricing model under the situation of centralized and decentralized decisionmaking,and provided the optimal pricing strategy combination of closedloop supply chain under stochastic disruption and stochastic demand.Finally,the numerical example illustrated how the supply disruption affected the optimal wholesale price and retail price.
Key wordslogistics and supply chain management;stochastic disruption;game theory;differential pricing
1引言
全球經濟的快速發展導致自然資源的嚴重短缺,為了經濟社會的可持續發展,研究如何對廢舊品回收再利用已經成了近幾年來國內外普遍關注的問題.為了應對廢舊品的回收再利用,各個國家制定了許多相應的法律法規.例如,美國在1984年頒布了《資源保護和回收法》(簡稱RCRA);日本在1991年實施了《資源有效利用促進法》;中國在1998年生效的《廢家用電器再利用法》等等.為了響應國家號召,且廢舊品再加工的成本通常情況下都比較低,所以大多數企業都參與了供應鏈的再制造過程,如施樂公司、惠普公司.因此對于閉環供應鏈的研究變得刻不容緩.
閉環供應鏈管理的目的是為了促進社會經濟與環境的綜合績效,從而使經濟和環境達到雙贏.所謂的閉環供應鏈是在傳統生產消費模式下增加了廢舊品回收再利用環節.目前國內外學者關于閉環供應鏈的研究主要集中在隨機需求、差別定價和協調問題等領域.Jianmai Shi等(2010)[1]研究了閉環供應鏈系統的最優生產和定價策略問題,其中假定新產品和再造品無差別定價,沒有考慮產品在差別定價下的隨機需求與回收對價格的影響.Geraldo Ferrer等(2010)[2]討論了具有差別定價的新產品和再造品的多周期生產和定價問題.JenMing Chen,ChiaI Chang(2012)[3]在合作和競爭情形下分析了再制造閉環供應鏈的策略問題,分析結果表明策略決策取決于兩種情形下再制造成本和競爭強度.Jie Wei,Jing Zhao(2013)[4]研究了閉環供應鏈不同渠道下不同選擇的問題,應用博弈論和模糊論獲得了公司的最優策略.Min Huang等(2013)[5]建立了零售商和第三方同時競爭回收舊產品的閉環供應鏈最優決策博弈模型,得到最優價格和回收策略,證明了回收渠道的最優決策與制造商和零售商的回收競爭強度有關.付小勇等(2014)[6]運用博弈理論方法建立了市場機制下處理商回收渠道選擇博弈模型,并用數值仿真分析了博弈均衡結果.Xiang Li等(2015)[7]研究了在隨機需求和隨機產量下的再制造閉環供應鏈的定價決策問題,發現了先再制造后定價策略有較低的再制造成本、較高的缺貨罰金和挽救價值.T.Maiti,B.C.Giri(2016)[8]在零售價格和產品質量依賴于需求的情況下,探究了具有第三方回收的閉環供應鏈決策問題,但其中新產品和再造品具有相同的價格和需求.B.C.Giri ,S.Sharma(2016)[9]考慮了在供應中斷下具有不確定需求和回收的閉環供應鏈系統,通過一些特殊分布得到供應鏈最優生產策略.大多數文獻的研究都是假定新產品和再造品在市場上銷售完全沒有區別,即按照相同的市場價格和需求出售.現實中,雖然能夠實現再造品質量、性能與新產品相同,但是消費者往往對兩種產品是加以區分的.
不同于以上文獻,這里主要研究了由制造商、零售商和第三方組成的第三方回收模型的閉環供應鏈系統.在新產品和再造品存在價格差異且兩者之間不是獨立的,各自的市場價格都會影響對方需求的情形下,討論了具有隨機中斷和隨機需求的閉環供應鏈最優定價策略問題.并在數值算例中分析了最優批發價、銷售價與中斷的關系.endprint
2模型假設及符號說明
考慮由一個制造商、一個零售商和一個第三方所組成的閉環供應鏈中第三方回收問題.制造商利用原材料和廢舊品生產新產品和再造品,制造商可以從兩個供應商處獲得原材料,其中主要供應商非完全可靠(供應可能中斷),次要供應商完全可靠,當然主要供應商的價格要低于次要供應商的價格.由于消費者對新產品和再造品的認知不同,因此制造商以不同的批發價批發給零售商,零售商再以不同的零售價賣給消費者.當這些產品壽命終結成為廢舊品時,第三方以一定的回收補貼價從消費者處回收,最后由制造商利用廢舊品進行再制造,將再造品與新產品以不同的價格進行銷售,形成一個完整的閉環供應鏈.
設新產品的單位生產成本、批發價和零售價分別為cm、w3和p1,再制造品的單位生產成本、批發價和零售價分別為cr、w4和p2.第三方從消費者處回收廢舊品,在交易過程中回收品的單位服務費用為At.制造商從回收品中獲得的單位利潤為ct.令=Fτ表示制造商與第三方的合同費用,它是回收率τ的函數,其中F是制造商的決策變量.主要和次要供應商的單位原材料批發價格為w1和w2,主要供應商發生供應中斷的概率是p,零售商對新產品和再造品的訂購量分別為Q1和Q2.新產品和再造品的庫存因子分別為z1和z2,且是外生變量.為了便于問題的討論,進一步假設:
(1)主要供應商的單位批發價格低于次要供應商的,即w1 (2)再造品的單位生產成本、批發價和零售價低于新產品的單位生產成本、批發價和零售價,即cr (3)廢舊品的回收率為τ(0<τ<1),即回收的廢舊品可全部用于再制造.回收廢舊品的固定投入成本是廢舊品回收率τ的函數,固定投入成本表示為Bτ2(B>0); (4)零售商對新產品和再造品的單位缺貨成本分別為s1,s2,單位產品的挽救價值分別為h1,h2; (5)對消費者而言,新產品與再造品互為完全替代品,新產品對再造品的價格具有需求彈性,再造品對新產品的價格也具有需求彈性. 基于以上假設,閉環供應鏈新產品和再造品的市場需求可以表示為 其中δ是產品的市場容量,θ(0<θ<1)為新產品需求的市場份額,α1和α2分別是新產品和再造品需求的價格敏感系數,β1和β2分別是新產品和再造品的交叉價格敏感系數.假設產品零售價對自身的影響大于交叉價格的影響,即0<βi 3分散式條件下閉環供應鏈回收定價模型 所謂分散式決策,是指制造商、零售商和第三方分別以各自的利潤最大化為決策目標,確定新產品和再造品的批發價、零售價、回收率及合同變量的決策模式.在分散式條件下,假設制造商與零售商的關系為Stackelberg博弈關系,且制造商為領導者,零售商為跟隨者,制造商決定決策變量F和新產品、再造品的批發價w3、w4,零售商根據制造商決定的批發價來決定新產品和再造品的零售價p1,p2,由第三方決定產品的回收率τ,各自都以其利潤最大化為決策目標進行定價.因此可以將分散式決策下閉環供應鏈的決策問題歸結如下: 分散式決策下閉環供應鏈的最優差別定價問題可以表示為如下的Stackelberg博弈模型. 下面的命題1和2給出了分散式條件下新產品和再造品的最優零售價和批發價,以及廢舊品的最優回收率和制造商的合同變量. 命題1在分散式決策條件下,把庫存因子z1,z2視為外生變量,對于固定的z1,z2,存在使零售商和第三方利潤最大的最優零售價格組合(p*1,p*2)和最優回收率ψ*. 證明容易驗證E[πr]關于p1,p2是嚴格聯合凹的,E[πr]關于τ是嚴格凹的,所以E[πr]關于p1,p2有最大值,E[πt]關于τ有最大值.由利潤最大化的一階條件可得到最優零售價p*1,p*2和最優回收率τ*分別為 顯然由E[πr]是關于p1,p2的凹函數,E[πt]是關于τ的凹函數,所以在滿足一階條件的情況下,零售商和第三方公司都獲得了最大的利潤. 注1存在足夠大的正常數B,當回收率0<τ<1時,有 B>ctAtG(α1+α2-β)(α1α2-β1β2). 命題2在分散式決策下,對于固定的z1,z2,存在使制造商利潤最大的最優批發價格組合(w*3,w*4),以及制造商的合同變量F*. 證明由注1可知,E[πm]關于w3,w4和F的Hessian矩陣的一階主子式對應行列式的值 二階主子式對應行列式的值 三階主子式對應行列式的值 因此E[πm]關于w3,w4和F是嚴格聯合凹的,所以在滿足一階條件的情況下制造商獲得最大的利潤. 由于E[πm]關于wM3,w4和F是嚴格聯合凹的,所以E[πm]關于w3,w4和F有最大值,由利潤最大化的一階條件立即得到最優批發價格w*3,w*4和合同變量F*分別為 4集中式條件下閉環供應鏈回收定價模型 所謂集中式決策,是指為了使整個閉環供應鏈利潤最大化,制造商、零售商和第三方通過協商共同決定批發價、零售價以及回收率的決策模式.因此,由式(1)、式(2)和式(3)得到集中式決策下閉環供應鏈的總利潤: 集中式系統的決策問題可歸為如下的最優化模型: 下面的命題3給出了集中式條件下新產品和再造品的最優零售價和最優回收率. 命題3在集中式決策下,存在使系統利潤最大的最優零售價格組合(p**1,p**2)和最優回收率τ**. 命題3的證明類似于命題1和命題2的證明,這里不再贅述.
5數值算例
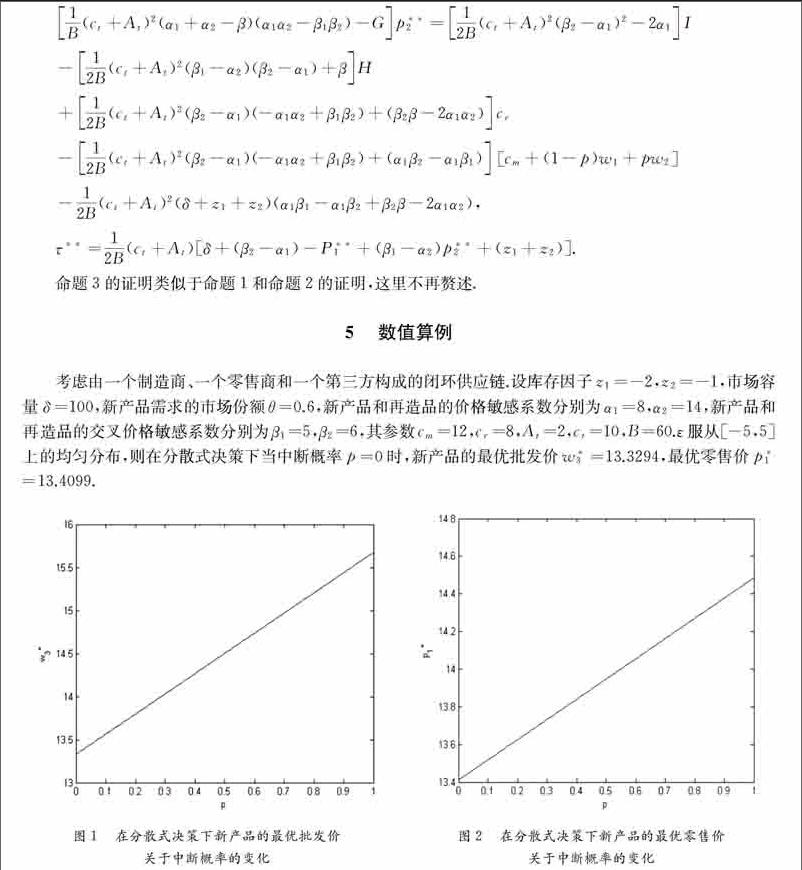
考慮由一個制造商、一個零售商和一個第三方構成的閉環供應鏈.設庫存因子z1=-2,z2=-1,市場容量δ=100,新產品需求的市場份額θ=0.6,新產品和再造品的價格敏感系數分別為α1=8,α2=14,新產品和再造品的交叉價格敏感系數分別為β1=5,β2=6,其參數cm=12,cr=8,At=2,ct=10,B=60.ε服從[-5,5]上的均勻分布,則在分散式決策下當中斷概率p=0時,新產品的最優批發價w*3=13.3294,最優零售價p*1=13.4099.
在以上參數假設下,中斷概率對最優的批發價和零售價會產生一定的影響.在分散式決策下,新產品的最優批發價和零售價關于中斷概率求導,得到最優批發價和零售價關于中斷概率是正相關的.對于給定的中斷概率p,得到最優批發價w*3和零售價p*1關于中斷概率的表達式,具體情況如圖1、圖2.圖1給出了在分散式決策下新產品最優批發價隨著中斷概率的變化情況.圖2給出了在分散式決策下新產品最優零售價隨著中斷概率的變化情況.
由圖1、圖2可以得到下面的注2.
注2在分散式決策下,新產品的最優批發價和最優零售價隨著中斷概率的增大而增加.因此,主要供應商發生中斷時,最優批發價格增加,零售商就會選擇完全可靠的次要供應商.相應的再造品的最優批發價和最優零售價與中斷概率的關系類似.
6結束語
研究了分散式和集中式情形下的第三方回收的再制造閉環供應鏈的最優差別定價模型,得到了新產品和再造品的最優定價策略組合和最優回收率及制造商的合同變量,并進一步分析了最優定價與中斷概率的關系.結果表明:新產品和再造品的最優批發價和最優零售價會隨著中斷概率的增大而增加.因此,在實際供應鏈運作中,若主要供應商發生中斷則最優批發價格增加,零售商就會選擇完全可靠的次要供應商來完成供應鏈的運作.本文只研究了制造商、零售商與第三方的閉環供應鏈系統,在實際生活中的真實情況遠比此復雜,因此還有待于我們深入研究.
參考文獻
[1]Jianmai Shi,Guoqing Zhang,Jichang Sha.Optimal production and pricing policy for a closed loop system[J].Resources,Conservation and Recycling,2010,55(6):639-647.
[2]Geraldo Ferrer,Jayashankar M,Swaminathan.Managing new and differentiated remanufactured products[J].European Journal of Operational Research,2010,203(2):370-379.
[3]JenMing Chen,ChiaI Chang.The coopetitive strategy of a closedloop supply chain with remanufacturing[J].Transportation Research,2012,48(2):387-400.
[4]Jie Wei,Jing Zhao.Reverse channel decisions for a fuzzy closedloop supply chain[J].Applied Mathematical Modelling,2013,37(3):1502-1513.
[5]Min Huang,Min Song,Loo Hay Lee,Wai Ki Ching.Analysis for strategy of closedloop supply chain with dual recycling channel[J].Internatioal Journal of Production Economics,2013,144(2):510-520.
[6]付小勇,朱慶華,趙鐵林.基于逆向供應鏈間回收價格競爭的回收渠道選擇策略[J].中國管理科學,2014,22(10):72-79.
[7]Xiang Li,Yongjian Li,Xiaoqiang Cai.Remanufacturing and pricing decisions with random yield and random demand[J].Computers Operations Research,2015,54:195-203.
[8]T.Maiti,B.C.Giri.A closed loop supply chain under retail price and product quality dependent demand[J].Journal of Manufacturing Systems,2015,37:624-637.
[9]B.C.Giri,S.Sharma.Optimal production policy for a closedloop hybrid system with uncertain demand and return under supply disruption[J].Journal of Cleaner Production,2016,112:2015-2028.endprint

