彈體破片分布及破碎性系數計算*

郭 超, 宮小澤, 李向東

(1 南京理工大學機械工程學院, 南京 210094; 2 中國白城兵器試驗中心, 吉林白城 137001)

彈體破片分布及破碎性系數計算*

郭 超1, 宮小澤2, 李向東1

(1 南京理工大學機械工程學院, 南京 210094; 2 中國白城兵器試驗中心, 吉林白城 137001)

為了研究彈體破片分布與材料、炸藥、殼體等的影響關系,以Mott模型為基礎,通過切片的方法對彈體進行了理論分析。分析了破碎性系數B的主要影響因素,通過量綱分析得到了破碎性系數B計算公式。通過該公式得出了13 mm壁厚彈體破碎性系數,且得到破片數和破片質量分布,并與試驗數據進行對比分析誤差小于5%,是因為回收率和端蓋的影響。提高破片回收率和排除端蓋的影響,該破碎性系數計算公式可用于彈體破碎性分布計算。

破碎性系數;破片分布;破片數;破片質量

0 引言

國內外對非預制破片的研究,使用最廣泛的是40年代的Mott[1]模型和70年代的Payman[2]模型,而破碎性試驗是測定破片數目、質量分布得到分布規律的一種常用試驗方法。

吳成等[3]通過仿真軟件,對小口徑榴彈起爆后殼體膨脹和破片形成過程進行了計算機模擬仿真;黃經偉[4-5]等通過破碎性試驗研究了大口徑榴彈自然破片分布規律;宋文淵[6]通過有限元建模對自然破片進行了建模分析。他們對破片數目及質量分布進行了研究,并得到了分布規律,同時也驗證了Mott模型的適用性,但是對于Mott模型中與材料相關的參數并沒有給出相應的分析。甄建偉、安振濤等[7]研究了彈丸破碎時殼體半徑與破片大小及數目的關系,得出了隨著圓環半徑的增大,破片數目成線性增長的規律,但是并沒有考慮殼體厚度的影響。陳醇[8]等研究了四種彈體材料對破片形成的影響,定性得出了隨著抗拉強度的增大破碎程度加深的結論,但是并沒有定量分析出具體變化關系。

文中基于試驗的基礎上,通過Mott模型研究彈丸殼體材料、殼體厚度、裝藥及半徑等影響因素對彈丸破碎性的影響,并對Mott模型中破碎性系數進行了研究,建立關于材料破碎性系數與影響因素之間的計算方程,并對結果進行評估分析。

1 破碎性試驗

1.1 試驗設計

圖1所示為試驗模擬彈結構,表1給出了試驗模擬彈殼體厚度tk、殼體質量mk、炸藥當量系數f、炸藥質量mz、炸藥內徑d等相關參數,殼體材料為50SiMnVB。

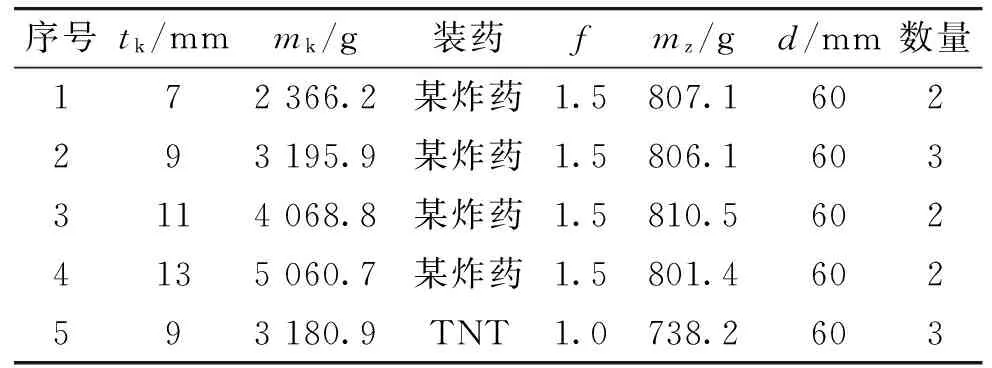
表1 模擬彈參數

1.2 試驗數據

不考慮質量小于0.1 g或0.3 g的破片,將回收的破片逐個稱重分組,得到了破片數及破片質量分布。

1)試驗模擬彈數據

分組處理,得到試驗破片統計表如表2及表3所示。

表2 破片數統計表

注：*表示彈殼內裝藥TNT，未注*表示某裝藥。

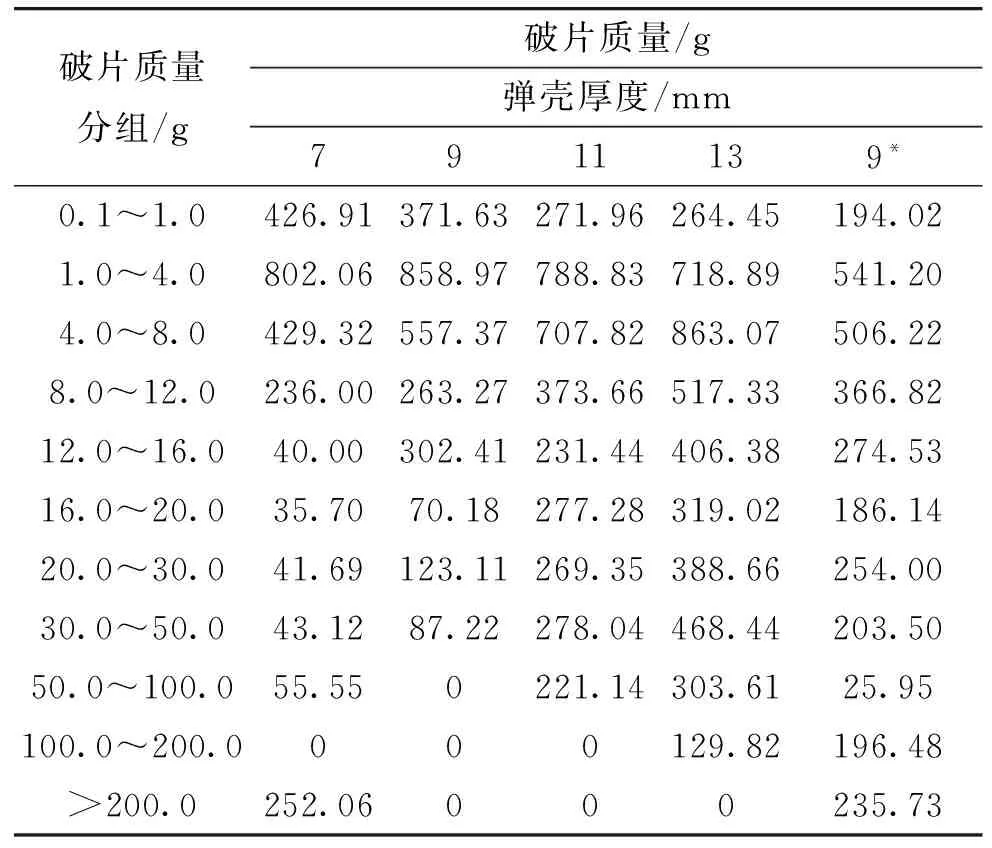
表3 破片質量統計表

注：*表示彈殼內裝藥TNT，未注*表示某裝藥。

2)某坦克炮殺傷榴彈數據

殼體材料為58SiMn的某坦克炮殺傷榴彈,破片數及破片質量分布如表4所示(該數據由其他實驗基地提供)。

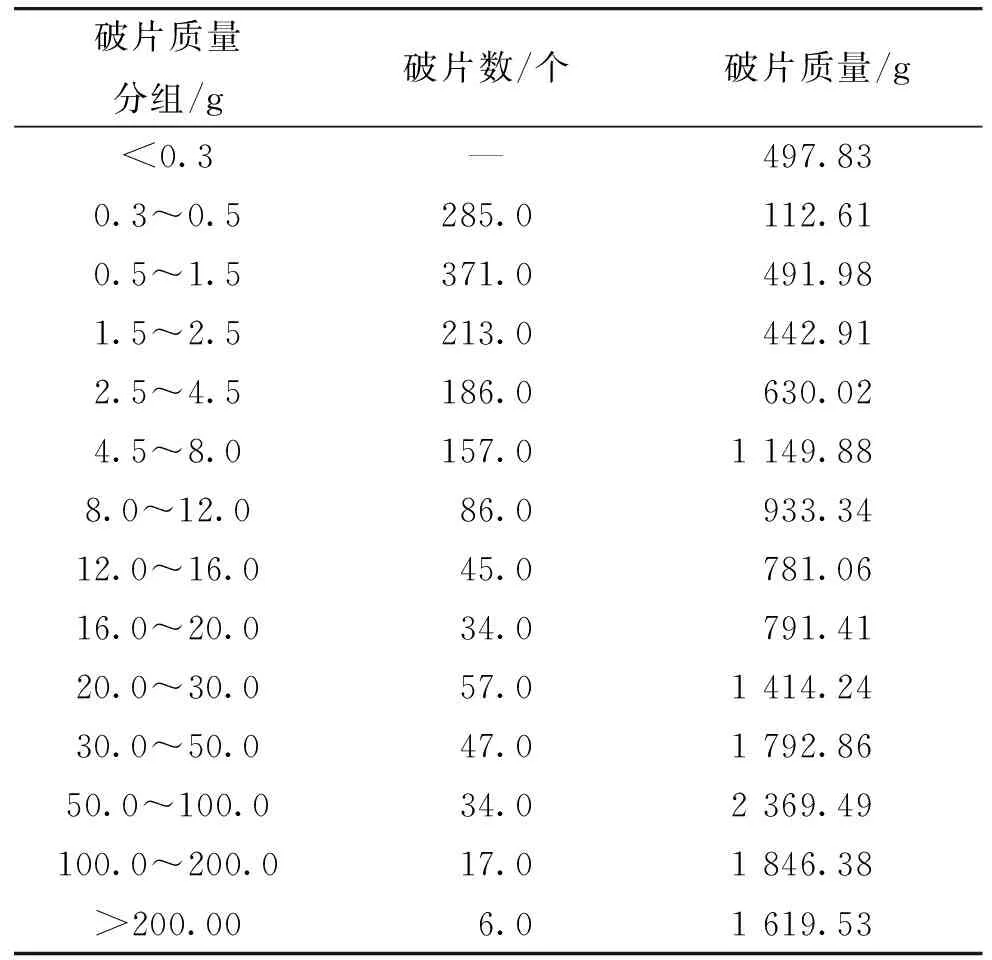
表4 某坦克炮破片分布表

1.3 理論分析

1.3.1 單元格劃分

沿著彈丸軸線垂直方向,將彈丸切割成不同單元格,劃分原則是將壁厚相近或相似部分劃為一個單元格(不考慮上下底部分),如圖2所示。

1.3.2 理論計算模型

于第i個單元格,破片質量特征參數計算公式為[9]:

(1)

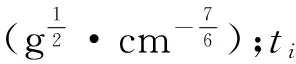
則由Mott公式[1]計算第i個單元破片總數為:

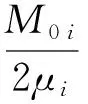
(2)

第i個單元格,單個破片質量大于mj時的破片累積數及累積質量為:

(3)

(4)

1.3.3 破碎性系數分析

累加所有單元格,可求得模擬彈單個破片質量大于mj的破片累計數N(>mj)和破片累計質量M(>mj)。

則在質量區間mj～mj+1,破片數與破片質量為:

N(mj～mj+1)=N(>mj)-N(>mj+1)

(5)

M(mj～mj+1)=M(>mj)-M(>mj+1)

(6)

假設破片在質量區間mj～mj+1的實際統計數為N實(mj～mj+1),實際統計質量為M實(mj～mj+1),則破片數殘差百分比與破片質量殘差百分比分別為:

式中:N實及M實表示回收的真實破片總數及破片總質量。

則得到殘差平方和S為:

(9)

采用最小二乘法對系數B進行分析,殘差平方和S最小時得到最佳系數B。根據我國殺傷破片對有生力量的殺傷標準[10]:動能大于98 J,破片質量不小于1 g,而實際有效殺傷破片質量為1.0～50.0 g,因而取質量為1.0～50.0 g的破片進行分析。

分析某炸藥、殼體壁厚7 mm、9 mm、11 mm及13 mm的模擬彈,破碎性系數B與殘差平方和S變化關系如圖3所示,得到破碎性系數B如表5。

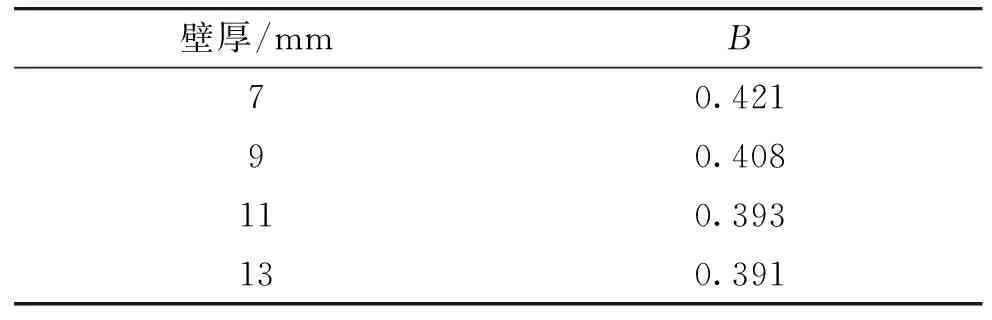
壁厚/mmB70.42190.408110.393130.391

同理,分析TNT裝藥、壁厚9 mm模擬彈,破碎性系數B與殘差平方和S的變化關系,得到破碎性系數B為0.507;某坦克炮破碎性系數B為0.346。

1.4 破碎性系數分析

再次，要有底線。中國共產黨從民主革命時期走到現在，經歷了各種艱難困苦，特別是在和平年代，社會主義市場經濟的飛速發展使一些不良思想有一定抬頭，這就要求思想的堅定和政治信仰的堅定就非常重要了。所以，這就意味著每一名黨員必須要牢固樹立底線意識，作為青年學生，在日常工作、生活中，我始終堅守底線，要有自己的原則，堅持自己的政治信仰，要立志為社會主義事業貢獻自己的力量。

1.4.1 基本假設

假設破碎性系數B的影響因素主要為厚徑比(殼體壁厚與炸藥直徑)、質量比(殼體質量與炸藥當量質量)、密度比(殼體密度與炸藥密度)和殼體極限抗拉強度,經量綱分析,得到基本公式:

(10)

式中:k1、k2、k3、k4、k5為相關系數;tk/De為厚徑比;ρk/ρz為密度比;mk/mz為質量比,其中mz=f·m,f為炸藥的TNT當量系數,m為炸藥質量(g);σb為殼體極限抗拉強度(MPa)。

1.4.2 相關系數求解

表6給出了材料及材料強度P(MPa)以及得到的最佳破碎性系數B值。

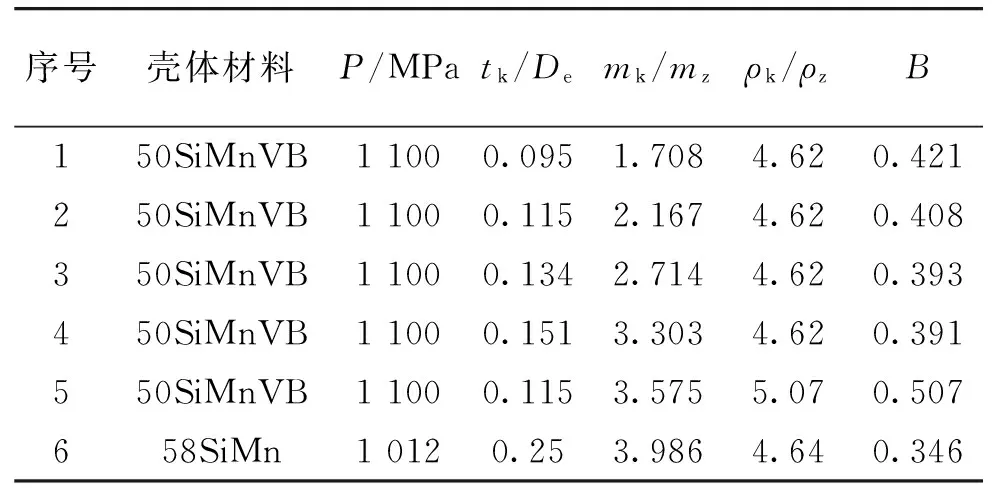
表6 相關參數

將表6序號為1、2、3、5、6(序號4用于結果檢驗)的數據代入式(10),通過Matlab求解,得到相關參數值如表7所示。

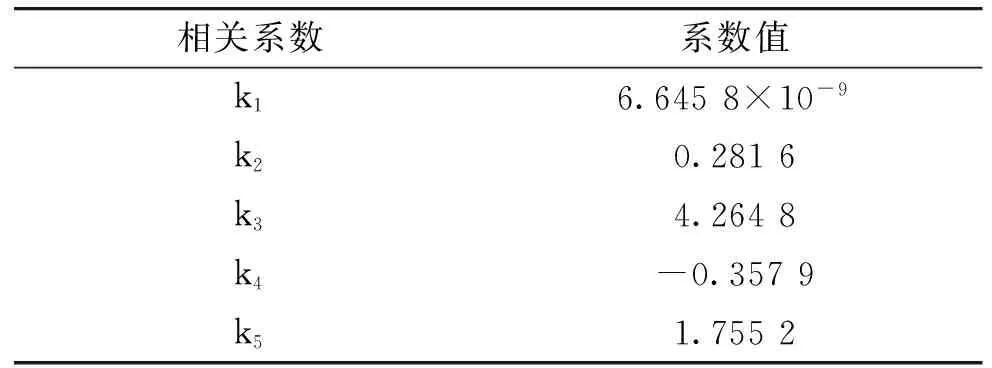
表7 相關系數值

則破碎性系數B的計算公式為:

(11)

1.5 破碎性計算

1.5.1 誤差分析

理論分析得到最佳破碎性系數B為0.391(見表6),將表6序號4各項參數代入式(11)求得破碎性系數為0.378,相對誤差為3.32%。

1.5.2 結果對比分析

將計算所得B=0.378及理論所得B=0.391代入式(1)～(6),得到破片數、破片質量分布結果,并與真實數據進行對比(見圖4～圖6)。

由圖4和圖5分析可得,在0.1～4.0 g之間,計算所得破片數及破片質量與理論破片數及破片質量相差不大,但較試驗破片數及破片質量偏大,其中1.0～4.0 g之間最為明顯,破片數相差100左右,破片質量相差200 g左右。分析原因主要是破片回收率引起,小質量破片回收較為困難;而在4.0～12.0 g之間,三者相差不大,計算所得數據可反映試驗分布情況;12.0 g以后,試驗數據較計算值及理論值偏大,且破片質量相差更為明顯。分析原因為試驗數據中包含有端蓋的影響,端蓋產生較多大質量破片,而計算數據中不考慮端蓋影響,所以計算值和理論值偏低。

但是從圖6分析來看,在0.1～50 g區間之間,破片平均質量相差不大。因而,計算所得破片的大小能夠反映真實破片的大小。

總之,提高試驗的回收率及減小端蓋的影響,計算數據與真實數據將更接近。所以,計算所得破片數及破片質量分布規律,可用于計算彈丸破碎性分布。

2 結論

1)結合理論與試驗數據,通過Mott模型及最小二乘法,得到模擬彈破片分布規律及理論破碎性系數。

2)研究了破碎性系數與殼體材料、殼體厚度、裝藥及半徑等影響因素的關系,并得到了破碎性系數的相關計算方程。

3)使用該方程進行了破碎性計算,并對計算所得數據、理論分布數據及試驗數據進行了對比分析,回收率造成小質量破片的偏差而端蓋造成大質量破片的偏差,但是破片平均質量分布即破片大小分布較吻合。所以提高試驗的回收率及減小端蓋的影響,該破碎性系數方程可用于計算彈丸破碎性分布。

[1] MOTT N F, LINFOOT E H. A theory of fragmentation：Ministry of supply: AC 3348[R]. [S.l.:s.n.],1943.

[2] WALSH B. The influence of geometry on the natural fragmentation of steel cylender： N73-25930[R]. [S.l.:s.n.],1974.

[3] 吳成, 艾東明, 李京. 小口徑榴彈破片質量分布規律計算模型 [J]. 彈箭與制導學報, 2002, 22(2): 35-37.

[4] 黃經緯, 李文斌, 鄭宇, 等. 大口徑榴彈自然破片形成過程 [J]. 兵工自動化, 2013, 32(11): 20-23.

[5] 黃經緯. 破片式戰斗部破片規律及破片對步兵戰車的侵徹作用研究 [D]. 南京: 南京理工大學, 2014.

[6] 宋文淵. 殺爆彈戰斗部自然破片有限元建模分析 [J]. 彈箭與制導學報, 2008, 28(3): 121-122.

[7] 甄建偉, 安振濤, 陳玉成, 等. 彈丸破碎時殼體半徑與破片大小和數目的關系仿真 [J]. 彈箭與制導學報, 2010, 30(6): 95-97.

[8] 陳醇, 李偉兵, 王曉鳴, 等. 彈性材料性能對破片形成的影響 [J]. 高壓物理學報. 2014, 28(5): 611-616.

[9] 陳醇. 三代炸藥爆炸加載下戰斗部殼體形變規律及破片性能研究 [D]. 南京: 南京理工大學, 2015.

[10] 李向東, 杜忠華. 目標易損性 [M]. 北京: 北京理工大學出版社, 2013: 38-61.

CalculationofFragmentationDistributionandFragmentationCoefficientofProjectile

GUO Chao1, GONG Xiaoze2, LI Xiangdong1

(1 School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China; 2 Baicheng Ordnance Test Center of China, Jilin Baicheng 137001, China)

In order to study the influence relationship between fragment distribution and materials, explosive, shell and so on, based on Mott model, theoretical research was carried out by slice method. The main influencing factors of the fragmentation coefficientBwere analyzed, and the formula of fragmentation coefficientBwas got by dimensional analysis. The fragmentation coefficient with 13 mm thickness and fragment quantity and fragment mass were obtained by the formula. Compared with experimental data, the analytical error of the fragment coefficientBcalculated by the formula was less than 5%, because of the influence of recovery rate and end cap. This formula could be used for the distributed computing of projectile brokenness by improving fragment recovery rate and excluding the influence of the end cap.

fragmentation coefficient; fragment distribution; fragment quantity; fragment mass

TJ410.1

A

2016-05-17

郭超(1990-),男,四川綿陽人,碩士研究生,研究方向:兵器工程。