具有零漂容忍度和非線性校正功能的電磁流量計儀表系數計算方法

汪春暢 許 偉 徐科軍 吳建平 梁利平

(合肥工業大學電氣與自動化工程學院)

具有零漂容忍度和非線性校正功能的電磁流量計儀表系數計算方法

汪春暢 許 偉 徐科軍 吳建平 梁利平

(合肥工業大學電氣與自動化工程學院)

針對部分國產電磁流量計通過了出廠標定，但再次校驗時誤差超差的問題，進行了大量實驗研究。確定造成小流速點超差的原因為儀表的零點漂移和非線性特性。分析了目前常用的幾種計算儀表系數方法存在的問題，提出分段線性擬合儀表系數計算方法。該方法同時兼顧小流量點和大流量點的誤差，為儀表的可能零點漂移預留較大的空間，克服儀表的非線性特性，使電磁流量計再次校驗或應用時都能滿足測量準確度的要求。

電磁流量計 超差 零點漂移 非線性 儀表系數 分段線性擬合

電磁流量計是基于電磁感應原理工作的，較為廣泛地應用于工業行業的水流量和漿液流量測量[1～3]。隨著工業的發展，對電磁流量計的測量準確度提出了更高的要求。然而，有些電磁流量計在出廠標定時能夠達到測量準確度的要求，但是，若再次檢驗(校驗)，此時往往需要重新夾裝,或者將一次儀表轉90°安裝,或者安裝到別的管道上(均符合安裝要求)，測試結果就達不到測量準確度的要求，主要表現為：在小流量點時測量誤差超過指標規定的范圍，即所謂的超差。這樣就不能保證現場的測量準確度，因為電磁流量計用于現場時肯定要重新夾裝。同時也無法滿足產品出口的要求，因為國外會對出口的產品進行校驗。

國內外學者曾深入研究過電磁流量計在管道90°轉角處安裝角度對測量誤差的影響，分析原因為流場紊亂，并計算出最佳安裝角度為45°，還研究了電磁流量計安裝未對準對其性能的影響[4,5]。但是，很少研究電磁流量計通過出廠標定，但再次檢驗超差的問題。這一問題嚴重影響了電磁流量計的實際測量準確度和國際市場的拓展。為此，筆者進行大量的實驗研究，尋找電磁流量計再檢驗時不滿足測量準確度的原因；分析目前常用的幾種計算儀表系數方法存在的問題；提出新的儀表系數計算方法，并進行實驗驗證，以使電磁流量計在有一定的零漂和非線性情況下也能保證其測量準確度。

1 影響測量準確度的因素

通過實驗和分析發現，電磁流量計標定時達到測量準確度的要求，而再次檢驗時小流速點超差，主要是由兩個因素引起的：一是電磁流量計的零點漂移，二是儀表的非線性特性。

1.1 零點漂移

零點是指在零流量情況下，電磁流量計輸出信號經過濾波和幅值解調后的感應電動勢值。零點漂移是指零點偏離固定值而往上或者往下漂動的現象。產生零點漂移的原因有：

a. 變送器中的電子器件，如運放、電容等的溫度漂移。電磁流量計安裝在測量現場，環境溫度會變化；電磁流量計工作時，本身的電子元器件也會發熱。若電子元器件本身的溫度特性不好，就會產生溫度漂移，從而造成流量不變時，輸出的電壓信號發生變化。

b. 勵磁電流不穩定。根據電磁流量計的工作原理，電極輸出的感應電動勢的穩定性取決于磁場的穩定性，而磁場的穩定性又取決于勵磁電流的穩定性。若勵磁電流不穩定，就會造成零點漂移。

由于誤差計算為測量值與真實值之差與真實值的比值，因此流速越小，零點漂移帶來的影響越大。

1.2 儀表非線性特性

通常認為電磁流量計的特性是線性的，即被測流速與測得的電動勢幅值之間是線性關系，可以y=ax來表示，其中，a為線性系數。若是線性特性，則不同流速點的儀表系數應該相同，而實驗數據表明，不同流速下的儀表系數是有差別的。在兩個不同的時間段標定電磁流量計在10個不同的流速點下的線性儀表系數，每個流速點均標定了兩次，發現不同流速下的線性儀表系數是不同的，且大流速與小流速的儀表系數相差較大。例如，在流速為5.5m/s時，線性系數為9.216 4；在流速為0.3m/s時，線性系數為9.257 2，相差了0.040 8。若選9.216 4為儀表系數，則測量誤差為0.0408/9.2164=0.443%，比較大。

2 計算儀表系數現有的方法

由于儀表材料和制造工藝方面的原因，電磁流量計不可避免地會存在一定的零點漂移和非線性特性。為此，必須研究合適的儀表系數計算方法，以便為電磁流量計的零點漂移留出一定的容錯空間，且能夠表征其非線性特性。所謂儀表系數是指可通過修改其數值而改變流量計計量性能的參數，它可以由一個或一組參數構成。目前，主要有4種計算儀表系數的方法：去零點法、最小二乘擬合法、基于示值誤差擬合法和均值法。筆者以容積法標定DN40mm電磁流量計為例來分析存在的問題。

2.1 去零點法

基于去零點法的儀表系數由一次項系數k和零點z組成，并由標定實驗數據計算得到。該方法認為感應出的電動勢信號中存在一個固定的幅值，即流速為零時輸出的幅值大小。根據這個前提，可在零流量狀態下計算出零點。得到零點的具體做法是：先設置k為1、z為0。在流量為零的情況下，用被檢表測量一段時間內的累計流量，根據時間和管道口徑等信息計算出零點，即為z值。得到一次項系數的具體做法是：在設置完z值后，k為1保持不變，將瞬時流量調節到量程中點，分別使用標準器和被檢表同時測量一段時間內的標準累計流量和測量累計流量，計算它們的比值，即為k值。

通過影響測量準確度的因素分析知道，在實際情況下，零點是會發生漂移的，而去零點法只是采用一個很短時間段內的測量結果作為零點，所以，當儀表長時間工作時，小流量點的測量誤差會受影響。為此，選擇一臺精度為0.5%的電磁流量計，由去零點法計算出儀表系數，在間隔數天的時間進行了兩次檢定實驗，檢定實驗結果如圖1所示，其中，第1次檢定的時間為t1～t2，測量誤差結果為曲線I，第2次檢定的時間為t3～t4，測量誤差結果為曲線Ⅱ。可見，當零點在正常范圍zmin～zmax內變化時，選擇的儀表在測量小流量時已經不能滿足精度要求。

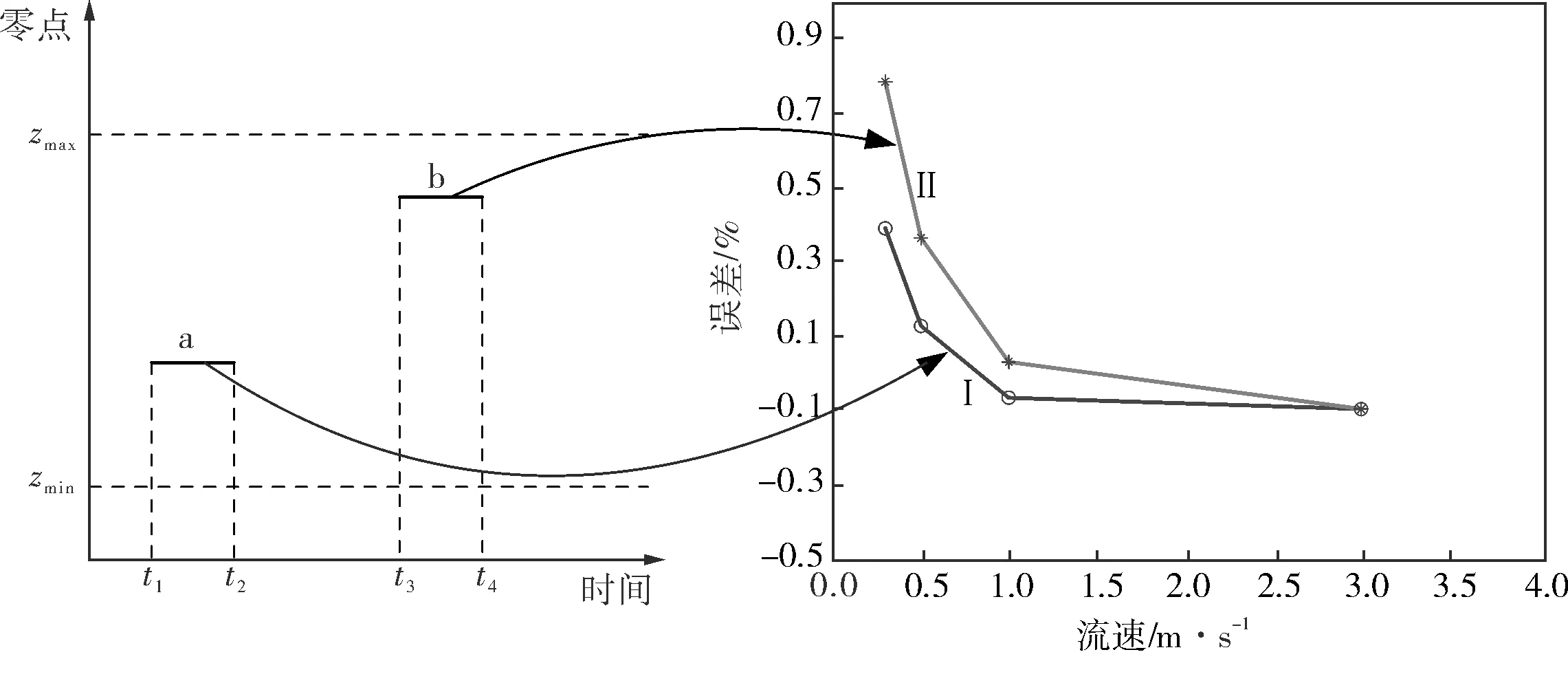
圖1 零點漂移下各流速點誤差的變化

2.2 最小二乘擬合法

該計算方法是基于絕對誤差大體相同的前提下對標定實驗數據進行最小二乘擬合，即擬合樣本中所有數據的擬合結果與標準值之間的絕對誤差大體一致[6,7]。但是，在檢定規程中，是采用示值誤差來表示流量計的準確度等級。示值誤差等于測量流速與標準流速的差除以標準流速。可見，同一準確度等級的電磁流量計，其測量流速越大，允許的絕對誤差就越大，而測量流速越小，允許的絕對誤差就越小。所以，采用基于絕對誤差的最小二乘法計算出儀表特征系數的電磁流量計在測量大流速時，示值誤差小；在測量小流速時，示值誤差比較大。最小二乘擬合法對當前數據擬合后不能保證小流速點的誤差較小，且可能超出測量準確度范圍。因此，該方法也沒有留出足夠的容錯空間來減小零點漂移對小流速點精度帶來的影響。

2.3 基于示值誤差擬合法

該計算方法把各個流速點的示值誤差的平方和最小作為數據擬合的目標，給予小流速點更多的關注，使測量流速與標準流速之間的示值誤差的平方和最小。該方法先設置電磁流量計的儀表系數中一次項系數和常數項系數分別為k=1和b=0。通過標定得到各個流量下的標準流速、平均感應電動勢，再對標準流速、平均感應電動勢進行擬合得到儀表系數k和b。測量流速yi與感應電動勢xi的關系如下：

yi=kxi+b

基于示值誤差擬合法是通過常數項系數b來實現對小流速點補償的，且對當前數據的補償效果較好，當儀表長時間工作，零點發生漂移時，小流量點的測量誤差可能會受影響。為此，選擇一臺精度為0.5%的電磁流量計，進行標定實驗并由基于示值誤差擬合法計算出儀表系數，在間隔數天后進行檢定實驗，實驗結果如圖2所示，可見，選擇的儀表在檢定實驗中小流量已經不能滿足精度要求。

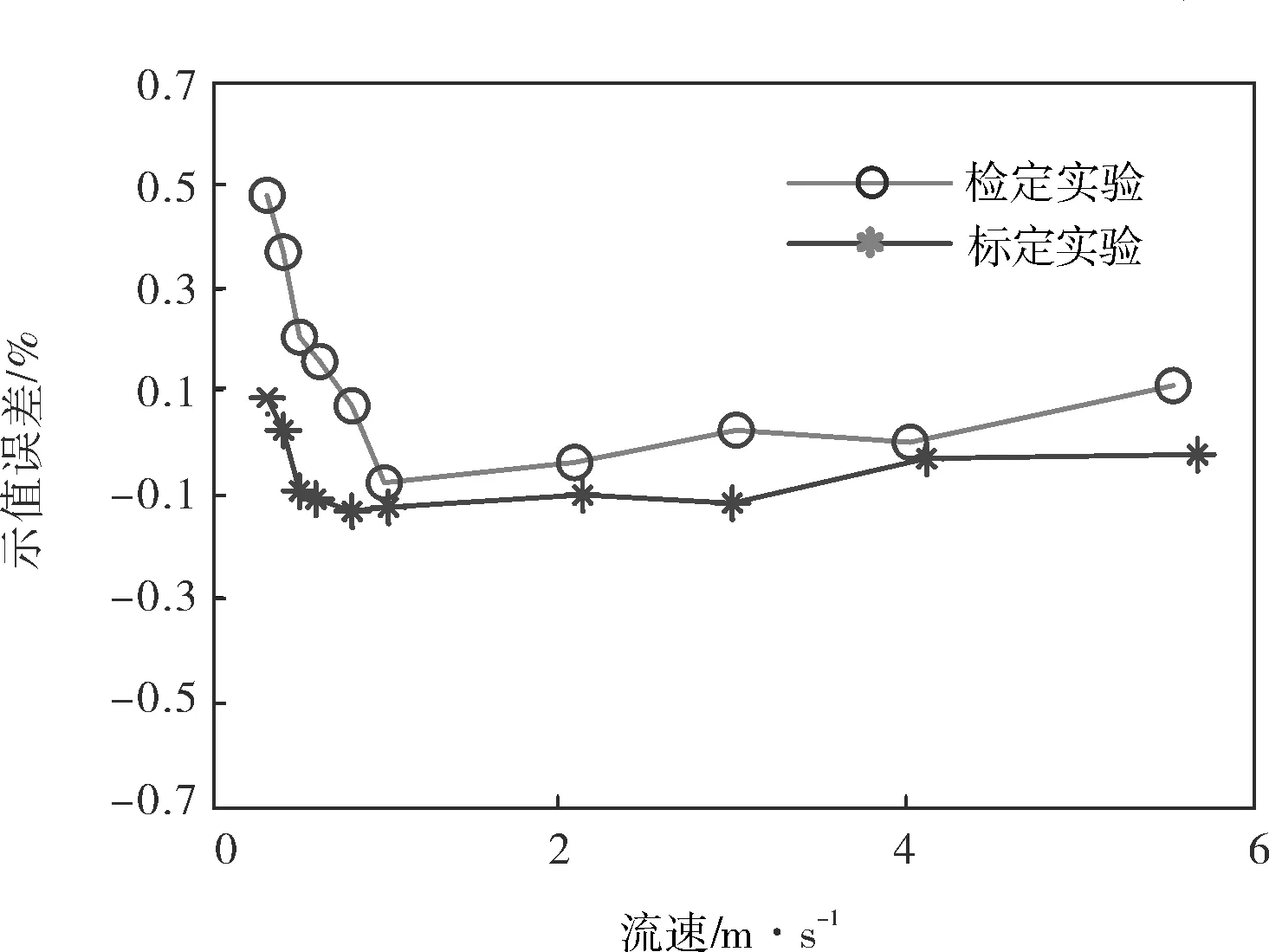
圖2 標定實驗和檢定時各流速點的示值誤差

2.4 均值法

該計算方法將若干個流速下的線性系數的均值作為儀表系數，只得到一個參數，即一次項系數k。按照與第3種儀表系數計算方法相同的實驗步驟，得到設定的若干個瞬時流量下的線性系數，且儀表系數為各瞬時流量點下的線性系數的平均值。

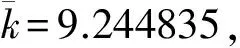
3 新的儀表系數計算方法

為了克服這些儀表系數計算方法的不足，筆者提出一種基于分段線性的電磁流量計儀表系數計算方法。該方法考慮到儀表的零點漂移和非線性問題，直接從每個流量點的線性系數出發，對不同流速點下的線性系數采用分段線性擬合，使小流速段的誤差較小(小于0.2%)；同時，使大流速段的誤差也較小。由于這種方法兼顧大流速和小流速，為零點漂移預留較大的容錯空間，從而保證再次檢驗時的測量準確度。一般來說，對不同流速點下的線性系數分兩段進行擬合，即大流速點和小流速點分別采用不同的儀表線性系數。若分兩段不能滿足要求，可適當增加分段數。下面以分兩段為例來說明該方法的步驟。

新的儀表系數計算方法具體步驟如下：

a. 選擇6個流速點，分別為1.0qmin、1.5qmin、2.5qmin、3.0qmin、6.0qmin和10.0qmin，或選擇5個流速點，分別為1.0qmin、1.5qmin、3.0qmin、6.0qmin和10.0qmin，其中，qmin為儀表所能測量的流速下限。由于隨著流速的減小，線性系數的最大相對變化率在增大，因此，在靠近小流速點的范圍內，流速點選得相對密些。

b. 根據選取的流速點，進行標定實驗，得出各個流速點的線性系數。

c. 觀察儀表線性系數的變化趨勢，找出線性系數最靠近儀表線性系數最大值和最小值平均值的流速點，并以此流速點作為分界點，把整個流速范圍分成大流速區間和小流速區間。

d. 分別計算大流速區間的儀表系數和小流速區間的儀表系數。對大流速區間的所有流速點的線性系數求平均，作為大流速區間的儀表系數；用同樣的方法可得到小流速區間的儀表系數。

針對DN40mm的電磁流量計，采用分段線性儀表系數計算方法計算出儀表系數，進行了兩次檢定實驗，兩次檢定實驗間隔數天，且第2次檢定實驗前將傳感器旋轉90°后重新安裝。兩次檢定實驗的流速點包括5.0、3.0、1.0、0.5、0.3m/s，每個流量點檢定3次，取3次誤差的平均值作為每個流量點的誤差，兩次檢定實驗的結果見表1、2。可見兩次驗證實驗的示值誤差均小于0.3%，重復性誤差均小于0.1，達到0.3級精度要求。

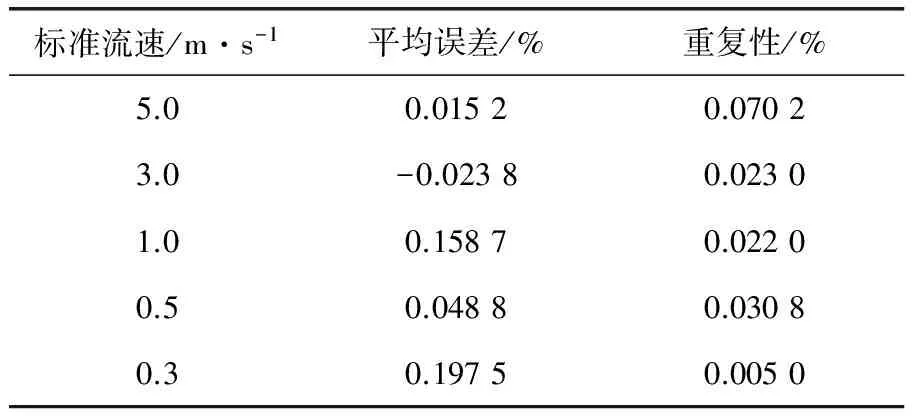
表1 第1次檢定實驗結果

表2 第2次檢定實驗結果

在某大型流量儀表廠的檢定站，采用筆者方法計算出儀表系數，并對DN300mm電磁流量計進行水流量校驗。按廠家要求，選取3個流速點進行校驗，分別為滿量程的10%、60%和100%。這兩次驗證實驗的示值誤差均小于0.3%，重復性誤差均小于0.1，達到0.3級精度要求。可見，采用筆者方法計算出的儀表系數，對重新夾裝的DN40mm和DN300mm電磁流量計進行校驗，測量準確度均為0.3級，有效地保證了電磁流量計的測量準確度。

4 結束語

提出的分段線性擬合儀表系數計算方法能兼顧小流速點和大流速點的測量誤差，且計算量小，應用方便。針對小流速點線性系數波動較大的問題，可以為小流速點提供更大的容錯空間，避免校驗時出現測量準確度不達標的問題。當零點漂移在一定范圍內時，不用去零點，標定和檢定的精度都能滿足要求。

[1] 張振, 徐科軍, 楊雙龍,等.具有快速響應的電磁流量計高低壓勵磁系統[J].電子測量與儀器學報, 2013, 27(6):562～571.

[2] 張然, 徐科軍, 楊雙龍,等. 采用梳狀帶通濾波的電磁流量計信號處理系統[J].電子測量與儀器學報,2012, 26(2):177～183.

[3] Liang L P, Xu K J, Wang X F, et al. Statistical Modeling and Signal Reconstruction Processing Method of EMF for Slurry Flow Measurement[J]. Measurement, 2014, 54(6):1～13.

[4] Lim K W, Chung M K. Numerical Investigation on the Installation Effects of Electromagnetic Flowmeter Downstream of a 90° Elbow-laminar Flow Case[J]. Flow Measurement & Instrumentation, 1999, 10(3):167～174.

[5] Peng Z, Cao Z, Xu L, et al. Influence of Installation Angle of Electromagnetic Flowmeter on Measurement Accuracy[C].IEEE International Symposium on Instrumentation and Control Technology.Piscataway,NJ:IEEE, 2012:195～199.

[6] 王浩，范廣涵，廖常俊，等.應用最小二乘法完善質量流量計的工作曲線[J].儀器儀表學報，2004，25(6)：770～772.

[7] 李穎，林洪生.基于相對誤差的曲線最小二乘擬合[J].沈陽師范大學學報(自然科學版)，2012，30(3):338～342.

CalculationMethodofElectromagneticFlowmeterCoefficientwithZero-driftToleranceandNonlinearCorrectionFunctions

WANG Chun-chang, XU Wei, XU Ke-jun, WU Jian-ping, LIANG Li-ping
(SchoolofElectricalandAutomationEngineering,HefeiUniversityofTechnology)

Aiming at some domestically-made electromagnetic flowmeters which passing ex-works calibration but troubled by the error which exceeding the specified range in re-examination, numbers of experimental studies were performed to show that, both zero-drift and nonlinear characteristics of the meter can result in this error at a small flow rate. Through analyzing the existing calculation methods for the instrument coefficient, a piecewise linear fitting method was proposed which having the errors at small and large flow rates taken into account to reserve a large space for the zero drift and to overcome the nonlinear characteristics. This makes the electromagnetic flow-meter satisfy accuracy measurement when they are re-examined or applied.

electromagnetic flow-meter, out-of-tolerance, zero drift, nonlinearity, instrument coefficient, piecewise linear fitting

TH814+.93

A

1000-3932(2017)09-0837-05

2017-05-05，

2017-05-21)

汪春暢(1992-)，碩士研究生，從事嵌入式系統及其應用的研究。

聯系人徐科軍(1956-)，教授，從事傳感器技術、自動化儀表和數字信號處理的研究，dsplab@hfut.edu.cn。