泰勒公式的應用探討

王 丹

（吉林建筑大學城建學院，吉林 長春 130014）

泰勒公式的應用探討

王 丹

（吉林建筑大學城建學院，吉林 長春 130014）

泰勒公式是高等數學中的一個重要定理,它可將一些復雜的函數近似表示為簡單的多項式函數.泰勒公式是研究函數的一個重要工具,在函數極限、導數的求解,方程根的存在性、不等式證明及近似計算中有著重要應用.本文對此進行了分析探討，以供參考.

泰勒公式；極限；高階導數

泰勒公式是將一個在x=x0處具有n階導數的函數f(x)利用關于(x=x0)的n次多項式來逼近函數的公式.泰勒公式的將指數函數、對數函數、三角函數及反三角函數等一些復雜的函數近似地表示為最為簡單的多項式函數來研究.是高等數學中的一個重要內容,在函數極限、導數的求解,方程根的存在性、不等式證明及近似計算中有著重要應用.

1 利用泰勒公式求極限

極限是高等數學中的重要基礎概念,連續、微分、積分等基本概念都是建立在極限概念的基礎之上.未定式極限是極限計算中一種常見形式,等價無窮小代換及洛必達法則是學生們常選用的兩個方法.但兩種方法都具有局限性，等價無窮小代換只能用于乘、除因子,作為加、減項的無窮小量不能隨意用其等價無窮小替換.應用洛必達法則是有些函數求導比較繁瑣甚至需要多次應用洛必達法則,計算量很大.此時,利用泰勒公式計算是一種更有效的方法.

解 當x→0時,由于

所以

該題利用帶有佩亞諾型余項的麥克勞林公式（泰勒公式在x=0處的展開式）,如用洛必達法則求該函數極限,需要用三次,且求導越來越復雜.由此例可看出,泰勒公式是計算函數極限的一個重要、有效的工具.

2 利用泰勒公式求高階導數

寫出函數y=f(x)泰勒展開式,再比較系數是求高階導數f(n)(x0)的常用方法,具體步驟為：

⑵題目給出一個具體的無窮階可導函數y=f(x)通過泰勒公式或麥克勞林公式展開成冪級數;

⑶根據函數展開式的唯一性,比較系數,即可求得f(n)(x0)或者f(n)(0).

例2 求函數y=ln(1-2x)在x=0處的n階導數f(n)(0).

解 ⑴由于y=ln(1-2x)無窮階可導,則將其展開為

因此y(n)(0)=-2n(n-1)!

例3 設函數c,且f"'(0)=1,求a的值.

此題若直接求,運算量非常大.泰勒公式是求函數階導數的一個基本方法.

3 利用泰勒公式證明方程根的存在

證明根的存在性的常用方法是連續函數的零點定理和羅爾定理,但一般地,若題設條件具有二階或二階以上的導數,應先考慮泰勒公式.

例4 設f(x)在[-1,1]區間上三次可微,證明存在實數)使得

令x分別為1,-1,得

其中 η1∈(-1,0),η2∈(0,1).上述兩式相減得

設 f"'(x)在[η1,η2]上的最大值、最小值分別為 M,m,則

根據介值定理,存在 ξ∈(η1,η2)?(-1,1),使得

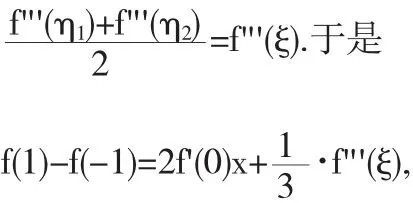
存在實數ξ∈(-1,1)使得

4 利用泰勒公式證明不等式

拉格朗日中值定理、泰勒公式是證明不等式的常用方法,當命題中含有f(n)(x)(n≥2)時常選用泰勒公式.

例5 證明若f(x)在[a,b]上存在二階導數,且f'(a)=f'(b)=0,則?ξ∈(a,b),使

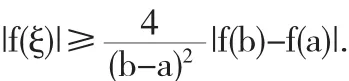
即?ξ∈(a,b),使

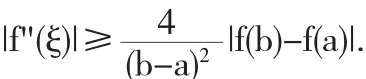
〔1〕苗文靜,王昕.關于泰勒公式及其應用的思考與討論[J].哈爾濱師范大學自然科學學報,2013,29(5)：18-21.

〔2〕王小玲.泰勒公式求極限[J].數學教學研究,2013,32(2)：55-58.

〔3〕黃先開,曹顯兵.2010年考研數學經典講義(理工類)[M].北京：中國人民大學出版社,2009.84-86.

〔4〕張宇.高等數學 18講[M].北京：北京理工大學出版社,2013.78-79.

O172

A

1673-260X（2017）10-0001-02

2017-07-24