自由活塞斯特林發動機動力活塞氣體作用效應

牟 健, 李 薇, 洪國同

(1.中國科學院理化技術研究所 北京，100190) (2.中國科學院大學 北京，100049)

10.16450/j.cnki.issn.1004-6801.2017.05.009

自由活塞斯特林發動機動力活塞氣體作用效應

牟 健1,2, 李 薇1,2, 洪國同1

(1.中國科學院理化技術研究所 北京，100190) (2.中國科學院大學 北京，100049)

為了能夠深入認識自由活塞斯特林發動機動力活塞的運行特性，找到提高自由活塞斯特林發動機效率的方法，對配氣活塞固定不動時的動力活塞的氣體作用效應進行了理論分析，并設計了動力活塞的單獨運動實驗，在此基礎上提出了動力活塞自然頻率的計算公式。研究了壓縮腔壓力波超前與滯后動力活塞位移兩種情況下動力活塞受到的氣體力的作用情況，采用旋轉矢量法闡述了氣體力的作用機理。當壓力波超前或滯后活塞位移小于90°時，一部分氣體力發揮了氣體彈簧的作用，使系統自然頻率增大；當壓力波超前或滯后活塞位移大于90°但小于180°時，一部分氣體力發揮了慣性力的作用，使系統自然頻率減小，且熱源溫度越高，系統的自然頻率越大。利用本實驗室的一臺自由活塞斯特林發動機進行實驗，驗證了上述氣體力作用的效應與規律，利用此理論計算系統自然頻率和實驗相差不超過2%，使得斯特林發動機成功啟動。

自由斯特林發動機； 動力活塞； 氣體作用效應； 自然頻率

引 言

隨著空間技術的發展，全球主要航天大國紛紛提出了一系列深空探測計劃，而這些計劃的實施也對空間電源提出了新的要求[1-5]。由于傳統電源某些方面的不足，利用斯特林循環將熱能(太陽能)轉化為電能的斯特林發動機，因其具有熱電轉化效率高，能利用低品位熱能等優點，逐漸得到大家重視[6-9]。斯特林發動機包括傳統的曲柄連桿斯特林發動機和自由活塞斯特林發動機[10]。自由活塞斯特林發動機不僅具有傳統斯特林發動機效率高、外燃性等優點，還因為取消了傳統斯特林發動機的曲軸連桿結構，具有噪聲和振動小、壽命長、體積小和功率密度大等優點[11]。相對于傳統的曲柄連桿斯特林發動機，自由活塞斯特林發動機研究起步較晚，發動機內部工作機理的了解不夠深入和完善。

對于自由活塞斯特林發動機而言，國外研究相對較多，國內還處于起步階段。目前，國內研究的主要問題集中于發動機的起動方面，即設計制造的發動機能否正常運轉。起動問題的關鍵是運動部件的動力學問題。雖然本實驗室已經成功起動自由活塞斯特林發動機，但是發動機的整機系統實驗只能測試到整機的系統熱力學和動力學參數，而忽略了各部件的動力學特性及其相互之間的影響規律，很難深入研究發動機的內在動力學特性、耦合過程及其對起動運行的影響規律。為此，本實驗室分別對自由活塞斯特林發動機的配氣活塞和動力活塞單獨運動的動力學特性進行了研究。其中，配氣活塞的氣體作用效應研究結果已經發表。這里主要介紹自由活塞斯特林發動機在固定配氣活塞的條件下，其動力活塞的動力學特性研究結果。主要包括活塞運動過程中的氣體作用效應和相關參數對氣體彈簧、氣體阻尼、氣體慣性以及動力活塞自然頻率的影響。

1 動力活塞振動系統的動力學模型

一臺完整的自由活塞斯特林發動機包括膨脹腔(熱腔)、壓縮腔(冷腔)、緩沖腔、配氣活塞、動力活塞、加熱器、回熱器、冷卻器、輸出電能的直線電機或輸出動能的機械裝置等。圖1為輸出電能的斯特林發動機示意圖。發動機成功起動后加熱器外部的熱能通過活塞帶動電機(或動力機械)運動轉化為電能(或動能)。

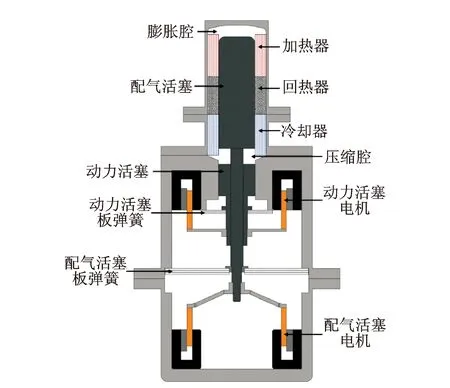
圖1 自由活塞斯特林發動機結構示意圖Fig.1 Schematic diagram of free-piston Stirling engine

自由活塞斯特林發動機主要是外部熱源通過加熱器加熱膨脹腔氣體，氣體加熱后膨脹推動活塞向外運動，然后腔體體積增大，并且氣體流向冷腔被冷卻，又使得腔體氣體壓力減小活塞又向里運動，如此往復運動。

起動問題一直是自由活塞斯特林發動機的關鍵問題。要解決起動問題必須清楚活塞的受力情況，而氣體力是活塞最為關鍵的一個力。雖然研究的動力活塞單獨運動的受力情況，但是此時和整機運動活塞受到的氣體力情況類似，對于研究自由活塞斯特林發動機氣體作用效應和解決整機起動問題具有重要意義。因此配氣活塞的板彈簧替換成剛性部件，使動力活塞在外界電機驅動時配氣活塞固定不動。圖2為動力活塞振動系統的模型圖。圖中：Ad為配氣活塞面積，m2;Ar為配氣活塞桿面積，m2;Pe為膨脹腔壓力，Pa;Po為緩沖腔壓力，Pa；Le為配氣活塞端面至膨脹端面的距離，m。

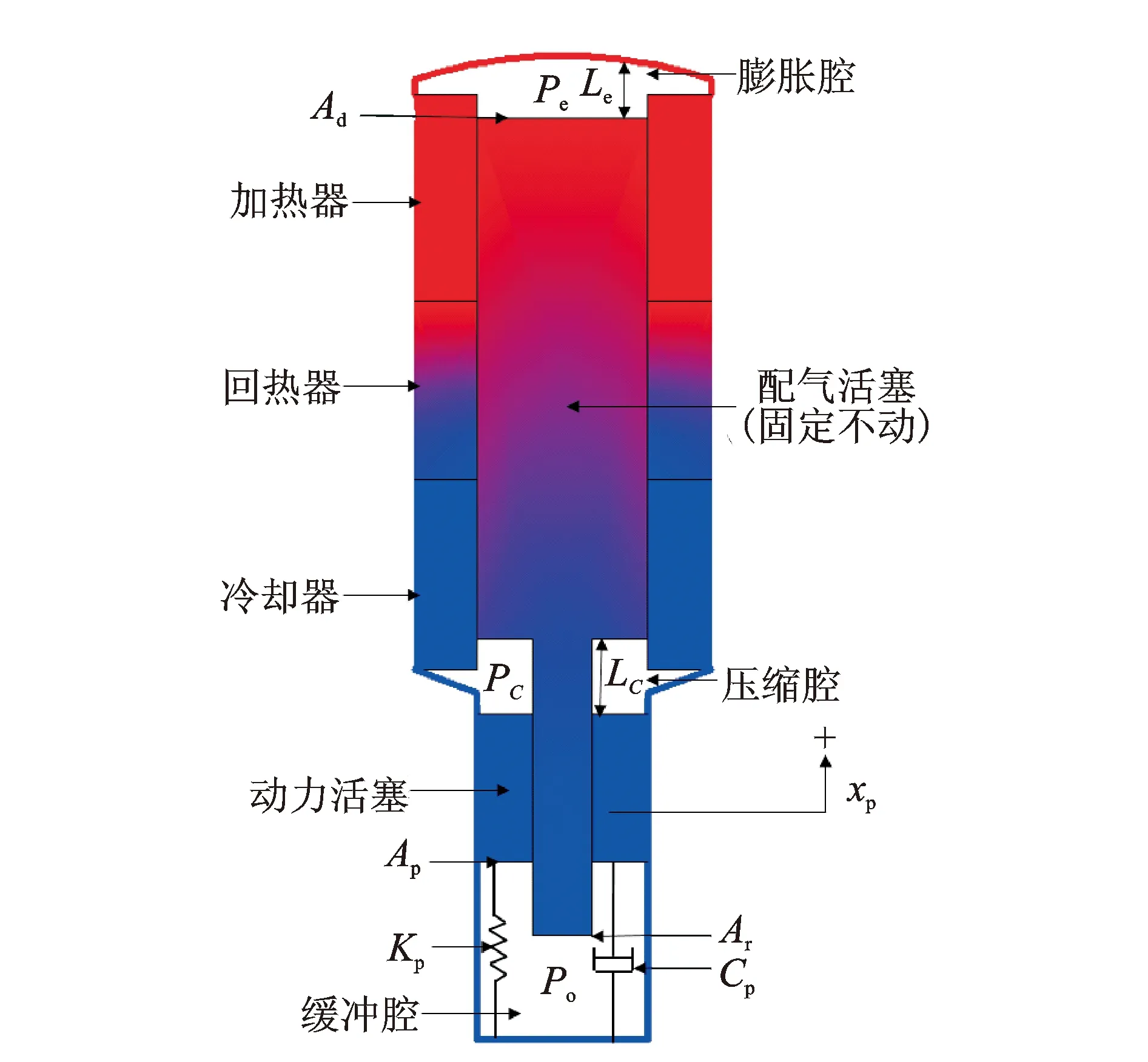
圖2 動力活塞振動系統模型圖Fig.2 The dynamics system model of piston

從圖2中看出， 動力活塞受到了壓縮腔壓力Pc向下的壓力，緩沖腔壓力Po向上的壓力和活塞運動過程中受到的阻力。同時因活塞與板彈簧和直線電機相連，受到了彈簧力和電機驅動力。其運動方程為

(1)

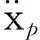
作用于動力活塞上的壓力

Fp=Ap(Pc-Po)=ApΔP

(2)

其中：Pc為壓縮腔壓力，Pa；Po為緩沖腔壓力，Pa；Ap為動力活塞面積，m2。

此模型中的壓縮腔壓力是根據Schmidt等溫模型[12]計算得出

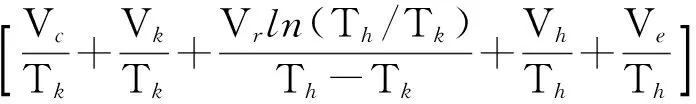
(3)

其中：Vc，Ve，Vr，Vk，Vh分別為壓縮腔、膨脹腔、回熱器、冷卻器以及加熱器的容積，m3；M為上述容積中氣體工質的總質量，kg；R為氣體常數；Th，Tk分別為熱源溫度和冷源溫度，K；緩沖腔壓力Po不變。

從動力活塞氣體驅動力的表達式可以看出，氣體驅動力與壓縮腔和緩沖腔的壓力差和動力活塞面積有關。由于斯特林發動機在高低溫熱源間工作，工作腔內的壓力變化不僅僅與工作腔的體積變化有關，同時受到冷熱源溫度的影響。隨著冷熱腔溫度的變換，壓力波幅值和相位也會發生改變，氣體力對動力活塞的作用效果也不同。下面就壓力波超前和滯后活塞位移兩種情況下的氣體壓力對動力活塞的作用效應進行分析。

2 壓力波超前位移時的氣體作用效應

2.1 超前相位α≤90°

根據位移與冷腔壓力波的大小和相位關系，可以畫出氣體力的矢量圖，如圖3所示。規定橫坐標為位移，并且橫坐標向左的方向為位移正方向，由于冷腔壓力波超前活塞位移，且小于90°，所以氣體作用力位于矢量圖的第三象限中，但由于冷腔的壓力PC對活塞的作用力與規定正方向的方向相反，所以轉動180°后位于矢量圖的第一象限中。

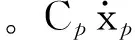
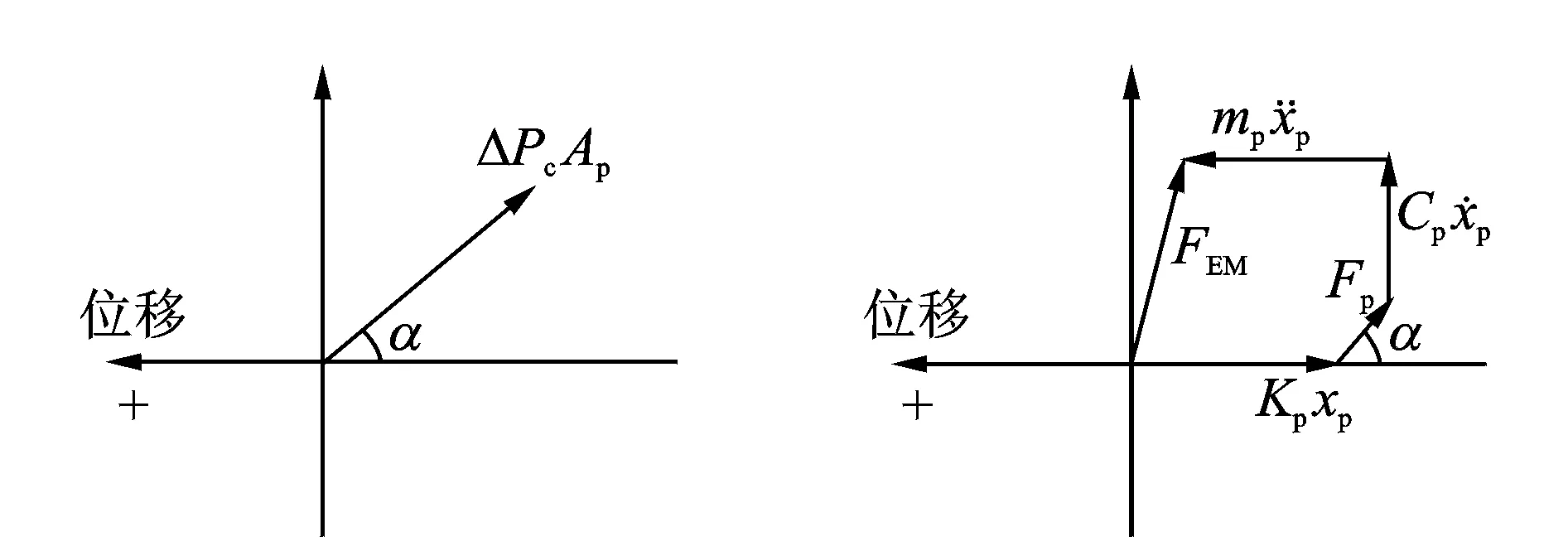
圖3 氣體力矢量圖(超前α≤90°) 圖4 動力活塞受力旋轉矢量圖(超前α≤90°)Fig.3 Vector diagram of gas force(leading α≤90°) Fig.4 Rotation vector diagram of force on the piston (leading α≤90°)

從圖4可知，氣體力可以分解為兩個力，一個是垂直于位移方向的氣體阻尼力，一個是平行于位移方向的氣體彈簧力。在特殊情況下，當α為0°時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體彈簧力的作用；當α為90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到氣體阻尼力的作用。在冷腔壓力波超前動力活塞位移相位小于90°的情況下，氣體阻尼的數值可以由下式計算

(4)

對于彈簧力而言，該情況可以認為機械板彈簧與氣體彈簧并聯，系統的總彈簧剛度等于板彈簧的彈簧剛度與氣體彈簧剛度相加。動力活塞的自然頻率由下式計算

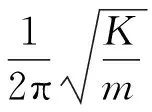
(5)

系統的總彈簧剛度為

K=(KpXp+Fpcosα)/Xp

(6)

氣體彈簧剛度為

Kg=K-Kp=Fpcosα/Xp

(7)

其中：Xp為動力活塞位移的振幅。

式(5)表示的只是在沒有阻尼條件下的活塞的自然頻率，但是實際中動力活塞不僅受到了機械阻尼還受到了氣體阻尼。因此用阻尼自然頻率才能更好地描述活塞運動的特征，阻尼自然頻率為

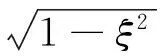
(8)

其中：fn為無阻尼自然頻率，Hz。

ξ為動力活塞阻尼率

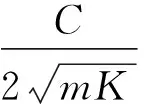
(9)

其中：C為系統的總阻尼，N·s/m；m為系統的總動質量，kg；K為系統的總彈簧剛度，N/m。

2.2 超前相位90°<α≤180°

圖5是在此相位關系條件下畫出的氣體力矢量圖，圖中依然規定橫坐標為位移，并且橫坐標向左的方向為位移正方向。由于冷腔壓力波超前動力活塞位移，且大于90°，所以氣體作用力位于矢量圖的第四象限中，同樣由于冷腔的壓力Pc對活塞的作用力與規定正方向的方向相反，所以轉動180°后位于矢量圖的第二象限中。

圖6給出了冷腔壓力波超前動力活塞位移相位大于90°但小于180°時的旋轉矢量圖。從圖6可知，氣體力同樣可以分解為兩個力：一個是垂直于位移方向的氣體阻尼力；另一個是平行于位移方向的氣體慣性力。所以，在計算動力活塞的自然頻率時，需要將系統的動質量與氣體慣性力中的質量相加。特殊情況下，當α為90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到氣體阻尼力的作用；當α為180°時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體慣性力的作用。

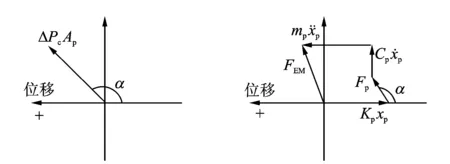
圖5 氣體力矢量圖(超前90°≤α≤180°) 圖6 活塞受力的旋轉矢量圖(超前90°≤α≤180°)Fig.5 Vector diagram of gas force(leading 90°≤α≤180°) Fig.6 Rotation vector diagram of force on the piston (leading 90°≤α≤180°)

此時，動力活塞的氣體阻尼和阻尼自然頻率仍然分別由式(4)和式(8)計算，系統的彈簧剛度僅為機械彈簧剛度，系統的總質量為

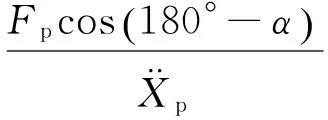
(10)

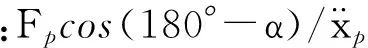
3 壓力波滯后位移時的氣體作用效應

3.1 滯后相位α≤90°

冷腔壓力波滯后動力活塞位移相位小于90°，所以氣體作用力位于矢量圖的第二象限中，但同樣由于冷腔壓力對活塞的作用力與規定正方向的方向相反，位于矢量圖的第四象限中。動力活塞最終受到的氣體作用力矢量關系如圖7所示。

圖8給出了冷腔壓力波滯后動力活塞位移相位小于90°時的旋轉矢量圖。當其他參數不變時，氣體力可以同樣分解為兩個力：一個是垂直于位移方向、且與阻尼力方向相反的力；另一個是平行于位移方向的氣體彈簧力，氣體彈簧與機械彈簧并聯。此時，動力活塞的阻尼自然頻率仍然由式(8)計算，系統總的彈簧剛度和氣體彈簧剛度的計算仍然分別采用式(6)和式(7)，而氣體阻尼為負阻尼特性，計算式為

(11)

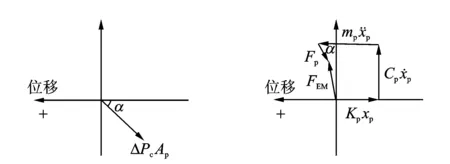
圖7 氣體力矢量圖(滯后α≤90°) 圖8 活塞受力的旋轉矢量圖(滯后α≤90°) Fig.7 Vector diagram of gas force(lagging α≤90°) Fig.8 Rotation vector diagram of force on the piston (lagging α≤90°)

特殊情況下，當α為0°時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體彈簧力的作用；當α為90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到抵制氣體阻尼力的作用。

3.2 滯后相位90°<α≤180°

根據位移與兩腔體壓力的大小和相位關系，同樣畫出了氣體力的矢量圖如圖9。由于冷腔壓力波滯后動力活塞位移，且大于90°，所以氣體作用力位于矢量圖的第1象限中，但由于冷腔的壓力Pc對活塞的作用力與規定正方向的方向相反，所以位于矢量圖的第3象限中。

圖10給出了冷腔壓力波滯后動力活塞位移相位大于90°但小于180°時的旋轉矢量圖。當其他參數不變時，氣體力可以同樣分解為兩個力：一個是垂直于位移方向、且與阻尼方向相反的力；另一個是平行于位移方向的氣體慣性力。此時，動力活塞的阻尼自然頻率仍然由式(8)計算，氣體阻尼為負阻尼，由式(11)計算，系統的彈簧剛度僅為機械彈簧剛度，系統總質量包括氣體等效動質量，計算式為(10)。

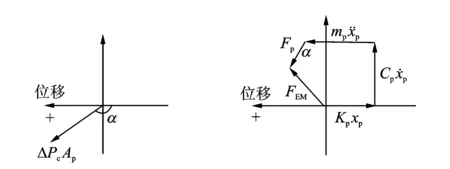
圖9 氣體力矢量圖(滯后90°≤α≤180°) 圖10 活塞受力的旋轉矢量圖(滯后90°≤α≤180°) Fig.9 Vector diagram of gas force(lagging 90°≤α≤180°) Fig.10 Rotation vector diagram of force on the piston(lagging 90°≤α≤180°)

特殊情況下，當α為180°時，兩腔體的氣體力與橫坐標平行，合力全部起到氣體慣性力的作用；當α為90°時，兩腔體的氣體力與橫坐標垂直，合力全部起到抵制氣體阻尼力的作用。

4 實驗結果及分析

該實驗是在本實驗室的自由活塞斯特林發動機上進行，通過加速度傳感器和壓力傳感器獲得動力活塞的加速度和壓縮腔壓力。然后，將這些實驗數據代入上述相應公式得到氣體力、氣體阻尼系數、系統總彈簧剛度、氣體彈簧剛度、系統總質量和系統自然頻率。同時采用共振法測得動力活塞的實際自然頻率，比較兩種自然頻率的大小以驗證上述氣體力作用效應理論的正確性。

板彈簧剛度為3 200 N/m，充氣壓力為1 MPa時，動力活塞位移和壓縮腔壓力在不加熱與加熱兩種情況下的變化，如表1所示。從表1可以看出，系統無論是否加熱，壓縮腔壓力波均超前活塞位移約14.4°；隨著熱源溫度的升高，相同活塞位移下，壓縮腔壓力波的幅值逐漸增大。圖11給出了動力活塞位移和壓縮腔壓力在不加熱與熱源溫度為500 ℃時的實驗曲線圖。

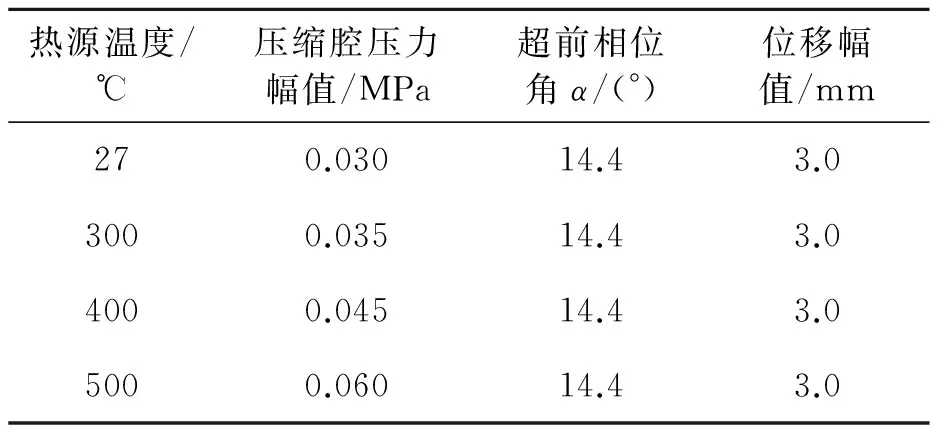
表1 不同熱源溫度下的實際運行參數

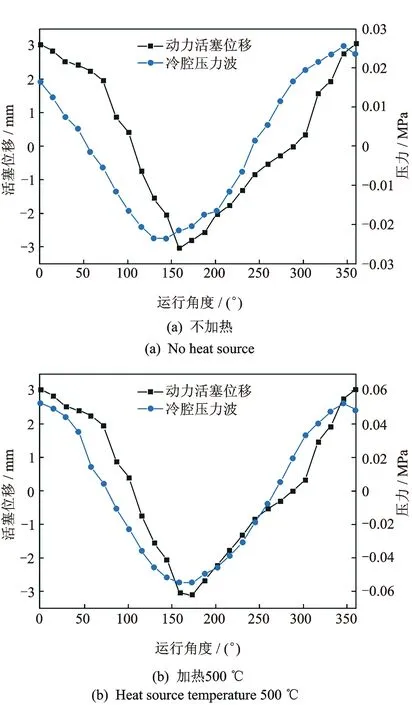
圖11 壓縮腔壓力與活塞位移實驗曲線圖Fig.11 Experimental data of displacement and pressure with and without heat sources

表2給出了在充氣壓力1 MPa時不同熱源溫度系統的機械阻尼、氣體阻尼和總阻尼數據。系統的機械阻尼是在真空條件下，采用激振的方法得到活塞自由振動的衰減曲線，通過計算阻尼率，再由式(9)得到。總阻尼則是實驗裝置在充氣壓力1 MPa不同熱源溫度下，同樣利用上述激振法測量得到阻尼率，再由式(9)計算得到。總阻尼減去機械阻尼就得到氣體阻尼實驗值。氣體阻尼的計算值則是由式(4)計算得到，其實驗值與計算值的最大相對誤差約為10%。由表2可知，氣體阻尼是動力活塞的主要阻尼，并且隨著熱源溫度升高，氣體阻尼占的比例更大。

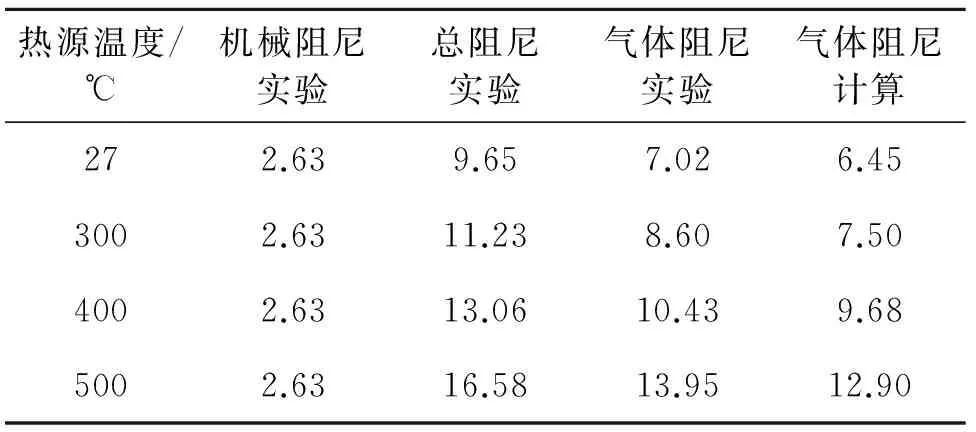
表2 不同熱源溫度下系統的阻尼值

表3給出了動力活塞自然頻率的理論值，從理論值可以看出，無論室溫下還是加熱條件下，氣體力均表現出氣體彈簧力和氣體阻尼的特性，不存在氣體慣性力作用，系統總的彈簧剛度增大，動力活塞自然頻率比無氣體時的明顯增大；隨著熱源溫度的升高，冷熱腔壓力波幅值增大，但壓縮腔壓力波超前動力活塞位移的相位不變，氣體彈簧力增大(氣體阻尼也增大，如表2)，整個系統的彈簧剛度和自然頻率逐漸增大。

為了驗證上述理論計算結果的正確性，采用共振法對動力活塞的阻尼自然頻率進行了實際測量。測量時，保持電機驅動功率不變，只改變頻率，測量不同頻率下活塞的位移，位移最大時對應的頻率即為自然頻率。實驗測得不同加熱溫度下系統的阻尼自然頻率如表3所示。從表3看出，系統阻尼自然頻率隨熱源溫度的變化規律與理論分析結果一致。

將表3中阻尼自然頻率的計算值與實驗值進行對比，可以發現計算值與實驗值一致性很好，最大誤差不超過0.6 Hz，從而間接驗證了筆者提出的自由活塞斯特林發動機動力活塞的氣體作用效應理論的正確性。

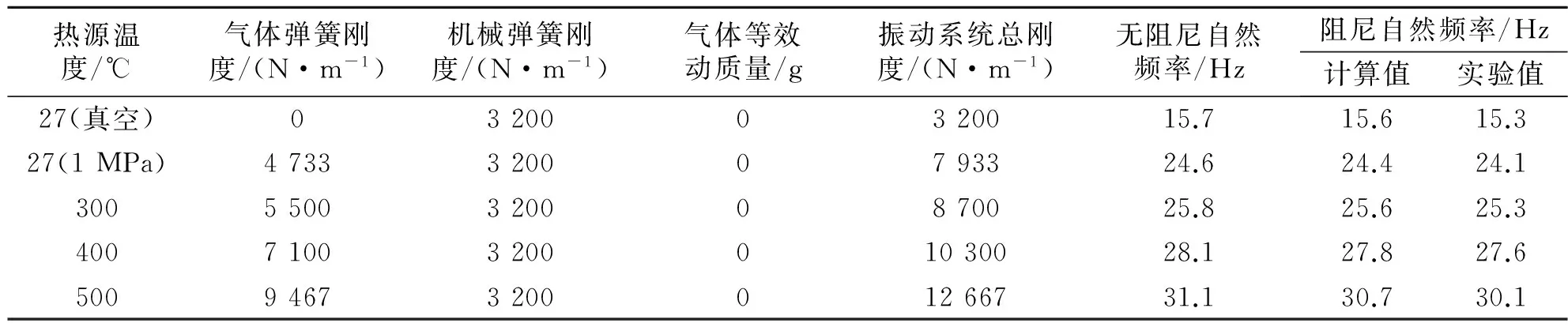
表3 不同熱源溫度下系統剛度和共振頻率的計算值及實驗值

5 結 論

1) 當系統壓縮腔壓力波超前或滯后配氣活塞位移相位α≤90°時，一部分氣體力起到了彈簧力的作用，此時認為氣體彈簧與機械彈簧并聯，系統總的彈簧力增大。

2) 當系統壓縮腔壓力波超前或滯后活塞位移相位90°<α≤180°時，一部分氣體力起到了慣性力的作用，系統總的質量等于機械動質量與氣體等效動質量之和，系統總的慣性力增大。

3) 當系統壓縮腔壓力波超前配氣活塞位移時，一部分氣體力表現為氣體阻尼作用，使得系統總的阻尼增大；當系統熱腔與壓縮腔壓力波滯后配氣活塞位移時，一部分氣體力則表現為氣體負阻尼作用，使得系統總的阻尼減小。

4) 對于自由活塞斯特林發動機而言，隨著熱源溫度的升高，壓力波超前動力活塞位移相位基本不變，實際測量為α≤90°；動力活塞存在明顯的氣體彈簧和氣體阻尼作用效應，這種效應隨熱腔工作溫度的升高而增大，系統阻尼自然頻率也隨之增大；動力活塞不存在氣體慣性作用效應。

[1] 李薇，牟健，洪國同.應變片用于斯特林發動機活塞位移的動態測量[J].振動、測試與診斷，2017，37(2)：372-377.

Li Wei, Mou Jian, Hong Guotong. Displacement measurement of free piston Stirling engine based on strain gauge[J]. Journal of Vibration, Measurement & Diagnosis, 2017，37(2)：372-377.(in Chinese)

[2] Mou Jian, Li Wei, Li Jinze, et al. Gas action effect of free piston Stirling engine[J]. Energy Conversion and Management,2016,110:278-286.

[3] Worms J C, Haerendel G. The european white paper on space: enough support for basic science[J]. Space Policy, 2004, 20(2): 73-77.

[4] Zhou Yi. Perspectives on Sino-US cooperation in civil space programs[J]. Space Policy, 2008, 24(3): 132-139.

[5] Bignami G F. European vision for space science[J]. Space Research Today, 2005(164): 8-15.

[6] Mou Jian, Hong Guotong. Startup mechanism and power distribution of free piston Stirling engine[J]. Energy, 2017, 123:655-663.

[7] Li Yaqi, He Yaling, Wang Weiwei. Optimization of solar-powered Stirling heat engine with finite-time thermodynamics[J]. Renewable Energy, 2011, 36(1): 421-427.

[8] Karabulut H. Dynamic analysis of a free piston stirling engine working with closed and open thermodynamic cycles[J]. Renewable Energy, 2011,36(6):1704-1709.

[9] Formosa F. Nonlinear dynamics analysis of a membrane Stirling engine: Starting and stable operation[J]. Journal of Sound and Vibration, 2009,326(3-5):794-808.

[10] 沃克 G.斯特林發動機[M]. 朱煒青，錢國柱，韓如，等,譯.北京:機械工業出版社, 1987：12-15.

[11] 賈紅書.100 W自由活塞斯特林發電機整機研制及性能分析[D].北京：中國科學院，2011.

[12] Thombarea D G, Verma S K. Technological development in the Stirling cycle engines[J]. Renewable and Sustainable Energy Reviews, 2008,12(1):1-38.

國家重點基礎研究發展計劃(“九七三”計劃)資助項目(613322)

2015-08-10；

2015-12-30

TH113.1; TK441+.1

牟健，男，1988年5月生，博士生。主要研究方向為自由活塞斯特林發動機。曾經發表《Startup mechanism and power distribution of free piston Stirling engine》(《Energy》2017,Vol.123)等論文。

E-mail:jmou@mail.ipc.ac.cn