離心力對旋葉式分離器壁面液膜界面不穩定性的影響

黃 振，肖澤軍，閆 曉，昝元峰，李 勇，袁德文

(中國核動力研究設計院，中核核反應堆熱工水力技術重點實驗室，四川 成都 610041)

離心力對旋葉式分離器壁面液膜界面不穩定性的影響

黃 振，肖澤軍，閆 曉，昝元峰，李 勇，袁德文

(中國核動力研究設計院，中核核反應堆熱工水力技術重點實驗室，四川 成都 610041)

本文對旋轉流場條件下離心力對旋葉式分離器壁面液膜界面不穩定性的影響規律進行了理論研究。首先利用勢函數對汽液兩相的動量方程和連續方程進行線性化處理。然后通過對無黏條件下液膜界面的受力分析，獲得汽液界面的動力學邊界條件和運動學邊界條件，結合線性化方程組建立液膜界面波的色散方程。根據力平衡原理獲得了液膜運動規律，并結合色散方程建立了界面不穩定發生的判定準則關系式。基于所獲得的理論模型編寫計算程序，對界面穩定性進行計算分析。研究發現，旋轉流場條件下的離心力能夠抑制旋葉式分離器壁面液膜界面不穩定的發生。

離心力；旋葉式分離器；液膜；界面不穩定性

旋葉式汽水分離器是飽和式蒸汽發生器的關鍵部件，直接決定著飽和式蒸汽發生器所產生蒸汽的濕度。蒸汽發生器管束區的蒸汽攜帶液滴進入旋葉式分離器，產生旋轉流動，液滴在旋轉離心力的作用下被分離到分離器壁面。

在旋葉式分離器內部，分離筒壁面的液膜與蒸汽之間存在軸向速度差，會使得界面出現波動，當滿足一定的條件時，界面波將出現不穩定，使得液膜發生泛化，產生二次液滴，影響分離器的分離性能。目前，在處理液膜泛化對分離器分離性能的影響時，主要采用了豎直環狀流下的液膜泛化速率關系式[1]。Tatterson[2]和Ishii[3，4]認為液膜界面的K-H不穩定可以作為液膜霧化的機理。

由于界面波不穩定性的復雜性，最早關于這方面的研究只針對無黏假設下的二維界面波展開，Scriven[5]于1960年對二維界面波展開理論研究，得到了無黏條件下界面波不穩定性的初步理論方程。而D.Y. Hsieh[6]在1989年基于無黏和無旋假設對二維直角坐標下的K-H不穩定展開進一步的理論研究，推導出了界面波色散方程。Daniel[7]給出了柱坐標系下，適用于無黏和黏性流體的通用勢函數分析方法。由于試驗技術的限制，目前國內外關于柱坐標下的界面不穩定的研究都集中于理論方面。但這些研究都針對的是無旋流場。在分離器內部，汽相流場為旋轉流場，分離器壁面液膜在旋轉流場作用下，其運動規律較豎直環狀流向的運動規律更復雜。在此條件下，汽液界面的受力也較非旋流場下的復雜。目前關于分離器表面液膜穩定性的影響還缺乏相應的研究。

本文將通過對分離器壁面液膜運動規律及界面受力分析，對分離器內旋轉流場條件下離心力對液膜界面不穩定進行理論研究。該研究可以作為旋葉式分離器液膜霧化研究的基礎，并為未來的分離特性模型建立和試驗研究提供理論支撐。

限于篇幅原因，文中部分模型的詳細推導過程和說明并未給出。模型中所有符號參數的說明均參考符號表。

1 液膜界面受力分析

旋葉式汽水分離器幾何結構如圖1所示。在無黏條件下，旋葉式分離器筒壁液膜界面受力分析示意圖如圖2所示，以指向筒壁外法線方向為正方向。

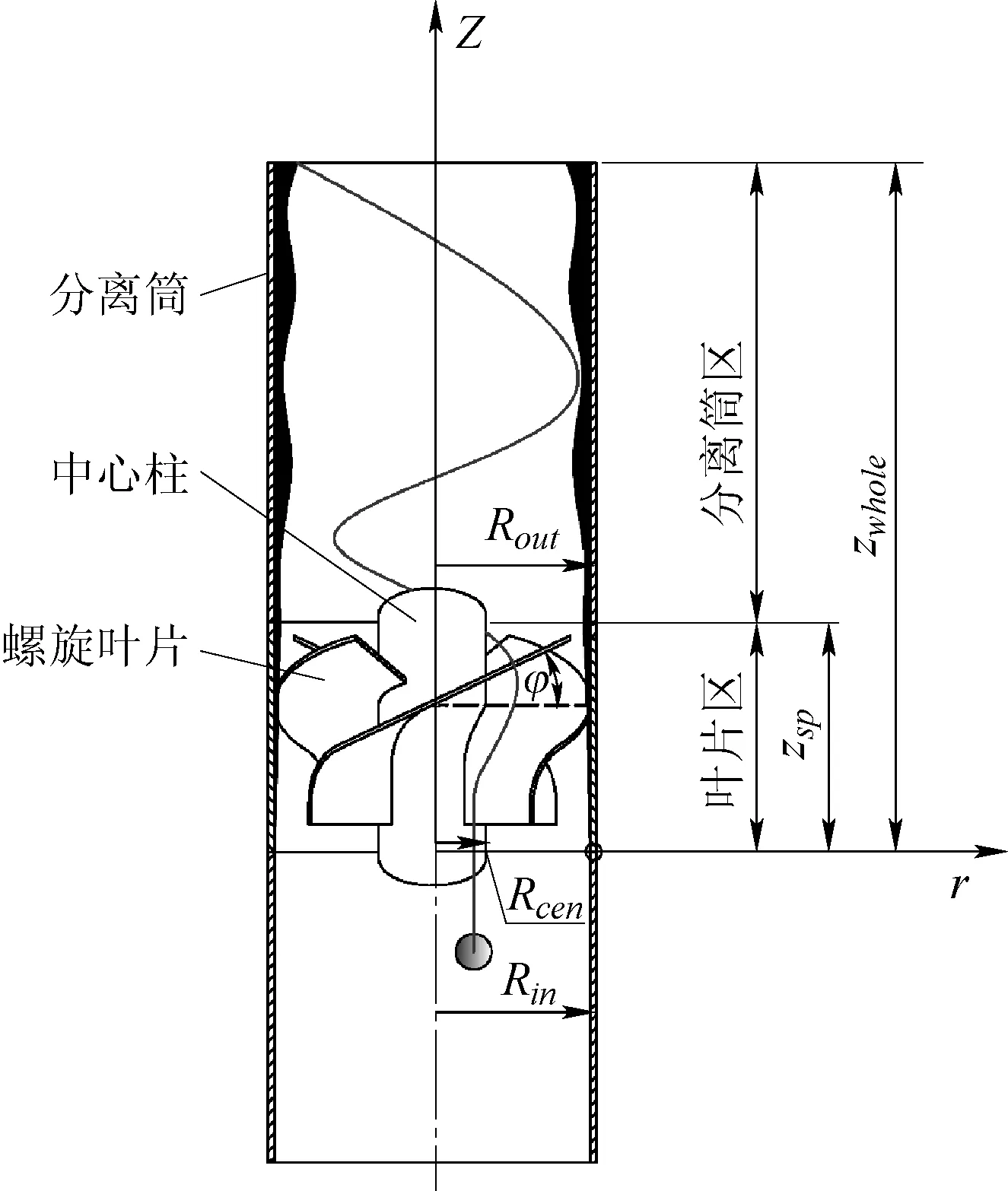
圖1 旋葉式汽水分離器結構示意圖Fig.1 Sketch Map of Cyclone Separator

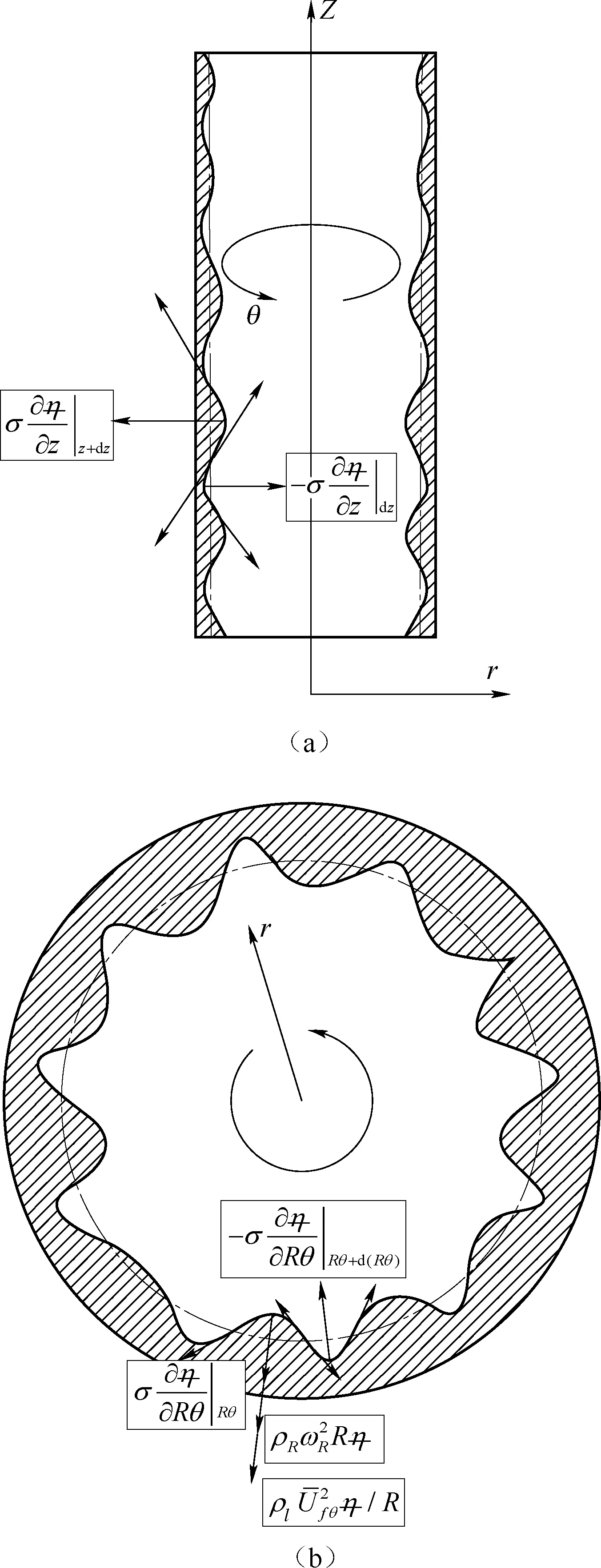
圖2 分離筒壁面液膜界面受力分析Fig.2 Stress Analysis of Film on Wall of Cyclone Separator

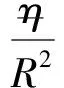
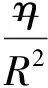
(1)

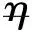
R——氣液界面半徑。

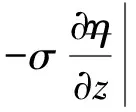
(2)

同理，z向單位長度的表面的θ向曲率在徑向方向表面張力的合力為：

(3)

根據式(1)至式(3)，單位面積液膜表面表面張力合力為：

Fσ=Fσ1+Fσ2+Fσ3

(4)

同時，液膜和液膜表面附近蒸汽因為旋轉運動，各自受到一個離心加速度作用，由此在各自流體中產生一個附加壓力(離心力)即：

(5)

(6)

當界面處于穩態條件下時，界面波平衡位置(如圖2中虛線所示)處的液膜表面兩側所受合力應保持平衡，即：

pf-Fσ-Fcl=pg-Fcg

(7)

將式(4)至式(6)代入方程(7)得：

(8)

在擾動條件下，界面位置函數可寫成如下形式：

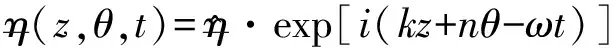
(9)

2 液膜界面不穩定模型

2.1 基本假設

① 液膜軸向速度及切向速度在徑向上均勻分布，即：

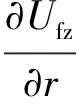
(10)

② 氣相角速度梯度可忽略，即角速度ωg=const，則切向線速度為：

Ugθ=ωgr

(11)

2.2 色散方程

無黏條件下，汽液兩相的動量方程的勢函數型式為：

i=f，g

(12)

將勢函數以下面的形式表示：

(13)

代入動量方程得

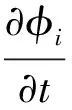
(14)

在旋葉式汽水分離器內部，蒸汽流速遠小于當地聲速，因此汽液兩相流體均可視作不可壓縮流體。根據質量守恒，基流在徑向上的速度分量可忽略，即：

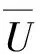
(15)

代入式(14)得小擾動下動量方程：

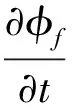
(16)

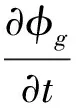
(17)

同樣利用勢函數對汽液兩相的連續方程進行變形得：

(18)

上述方程為修正貝塞爾方程[8]，其解為：

(19)

通過對界面特性分析，可以獲得汽液界面的運動學邊界條件：

(20)

聯合變形后的動量方程和界面的受力分析，得界面動力學邊界條件為：

(21)

本研究不考慮在切向出現的界面波動，既切向波數n=0，同時為方便求解，以R表示分離筒半徑，以h表示液膜厚度。將式(19)代入式(20)和式(21)，經過數學求解，得到無黏條件下汽液界面的色散方程為：

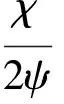
(22)

式中：

ψ=[(β-α)ρl+(α-γ)ρg]

χ=[2M(β-α)ρl+2N(α-γ)ρg]

δ=[(β-α)ρlM2+(α-γ)ρgN2-ξD+λD]

α=-I0[k(R-h)]·I1[k(R-h)]·K1[kR]

β=K0[k(R-h)]·I1[k(R-h)]·I1(kR)

γ=-I0[k(R-h)]·I1(kR)·K1[k(R-h)]

ξ=-k·[I1[k(R-h)]]2·K1(kR)

λ=-k·I1[k(R-h)]·K1[k(R-h)]·I1(kR)

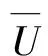
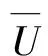
只有當：

4ψδ-χ2≤0

(23)

即：

+[ρl(β-α)+ρg(α-γ)]·(λ-ξ)·

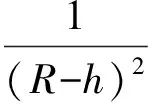
(R-h)-ρgωg2(R-h)]≤0

(24)

時，色散方程w的解為實數，此時根據式(13)可以看出勢函數的波動項的指數相關項是虛數，這就意味著波動項不會隨著時間增長，即界面擾動才能不隨時間增長，即兩個解都是穩定的。

2.3 液膜厚度及流速計算模型

色散方程涉及蒸汽和液膜的流速、液膜的厚度等變量。在旋葉式分離器內部，液膜受到旋轉蒸汽流的作用，其厚度與運動規律有其自身的特點。在本研究中只考慮分離筒區域的液膜運動，將液膜流動分為軸向運動和切向運動。

2.3.1 汽相流速

根據質量守恒和三角函數定理，可以得到汽相的軸向流速和切向流速。

葉片器汽相軸向流速：

(25)

分離筒區汽相軸向流速：

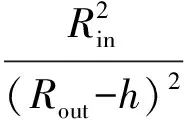
(26)

葉片區汽相旋轉角速度：

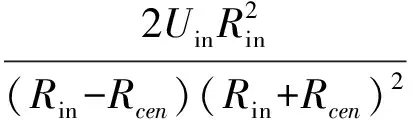
(27)

分離筒區汽相旋轉角速度：

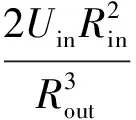
(28)

2.3.2 液膜的軸向流速及液膜厚度

通過對液滴在蒸汽流場中的受力及運動規律分析，可以獲得液膜質量流量隨軸向位置的變化規律

(29)

首先考慮液膜厚度及軸向流動。分離筒內液膜計算模型為[9]：

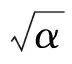
(30)

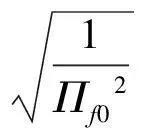
(31)

(32)

Πg02=1+C·X+X2

(33)

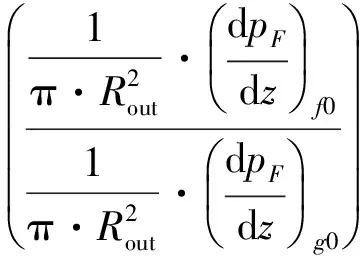
(34)

式中，C的值取決于具體的工況；Jf為液膜的表觀流速，本研究中將軸向各位置處未被分離的液滴與蒸汽共同以等效的蒸汽表觀流速Jg表示。即：

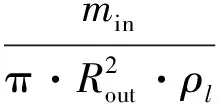
(35)

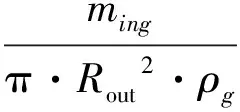
(36)

相應的雷諾數為：

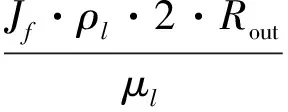
(37)

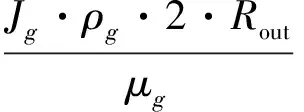
(38)

相應的摩擦系數為：

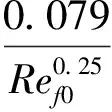
(39)

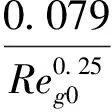
(40)

則液膜的平均流速為：

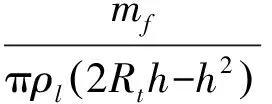
(41)

2.3.3 液膜切向流速

液膜沿切向流動受到兩個力的作用，一個是壁面對液膜的切向摩擦應力，一個是氣液界面氣相對液膜的切向摩擦應力。穩態條件下，液膜處于受力平衡狀態，即：

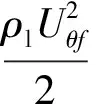
(42)

式中，fi為液膜界面切向摩擦系數，fw為液膜與壁面的摩擦系數，其計算模型如下[10]：

fw=0.079[4hUθfρl/μl]-1/4

(43)

(44)

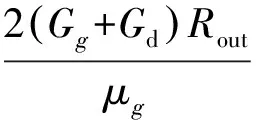
(45)

在本研究中考慮到隨著液滴的分離，液膜厚度可能在軸向上發生變化，將分離器的分離筒均勻分為10段(j=1，2，…，10)，在分離筒每組分段上，聯合式(29)至式(45)，求解每段液膜的軸向流速、切向流速和液膜厚度。

3 汽液界面不穩定性分析

3.1 工況參數

基于前述的理論模型，開發了相應的計算程序對分離器壁面液膜的不穩定進行分析，分離器的幾何結構參數如表1所示。計算工況如表2所示。

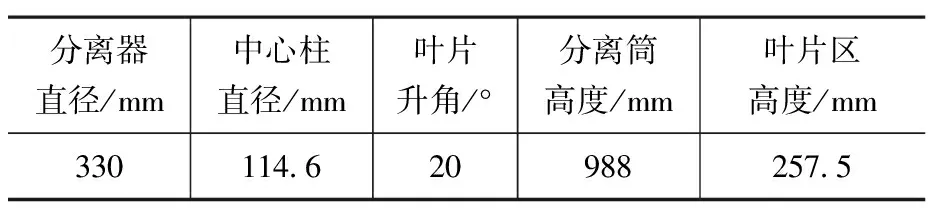
表1 分離器幾何結構參數Table 1 Geometry Parameters of Cyclone Separator

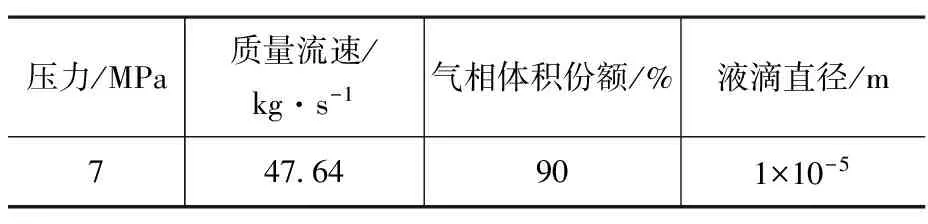
表2 有旋與無旋對比的計算工況Table 2 Conditions for contrast between rotation and irrotation

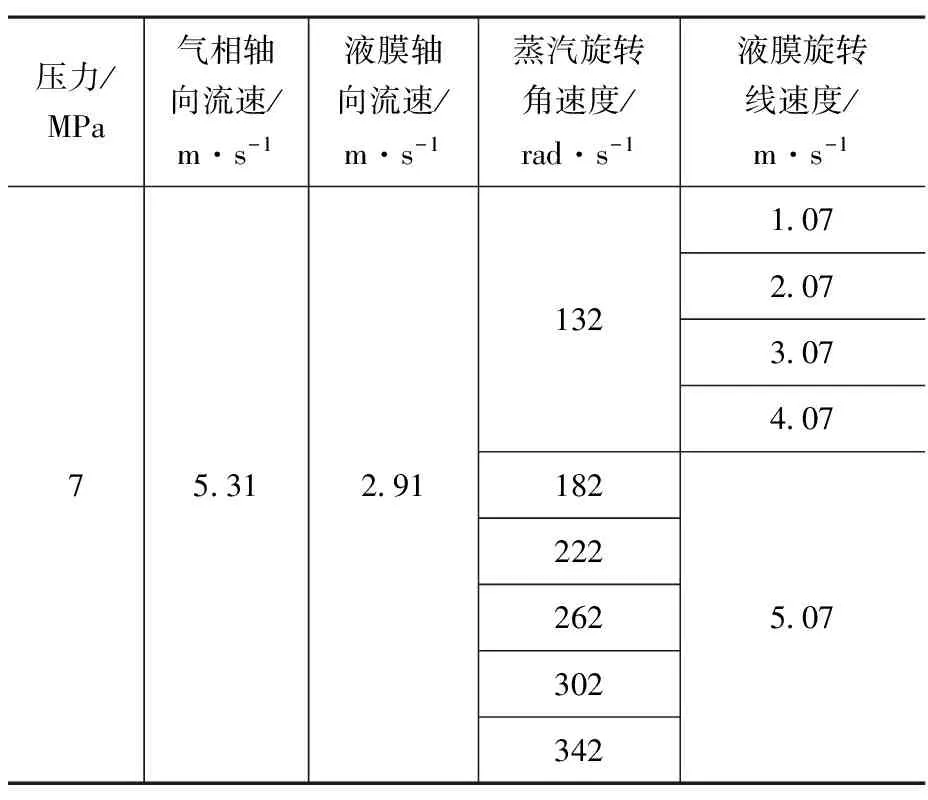
表3 各相離心力影響的工況參數Table 3 Conditions for effect of centrifugal force of each phase

3.2 離心力對液膜界面穩定性的影響

本文首先分別對離心力作用下和無離心力作用下的界面穩定性進行了計算。所得各段液膜(j=1，2，…，10)的f(k)隨波數的變化規律如圖3和圖4所示。從圖中可以看出，在相同的工況條件下，離心力作用下的界面處于穩定狀態(f(k)<0)，而無離心力作用下的界面處于不穩定狀態(f(k)>0)。由此可以得出，離心力對界面波的發展起著約束作用，能夠抑制界面不穩定的發生。

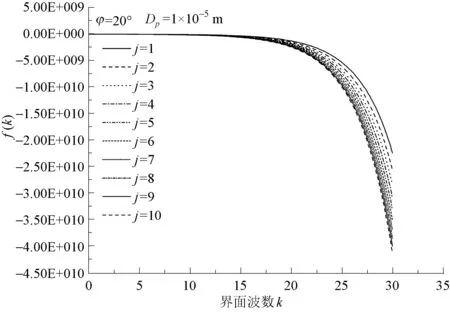
圖3 離心力作用下的f(k)Fig.3 f(k)with Effect of Centrifugal Force

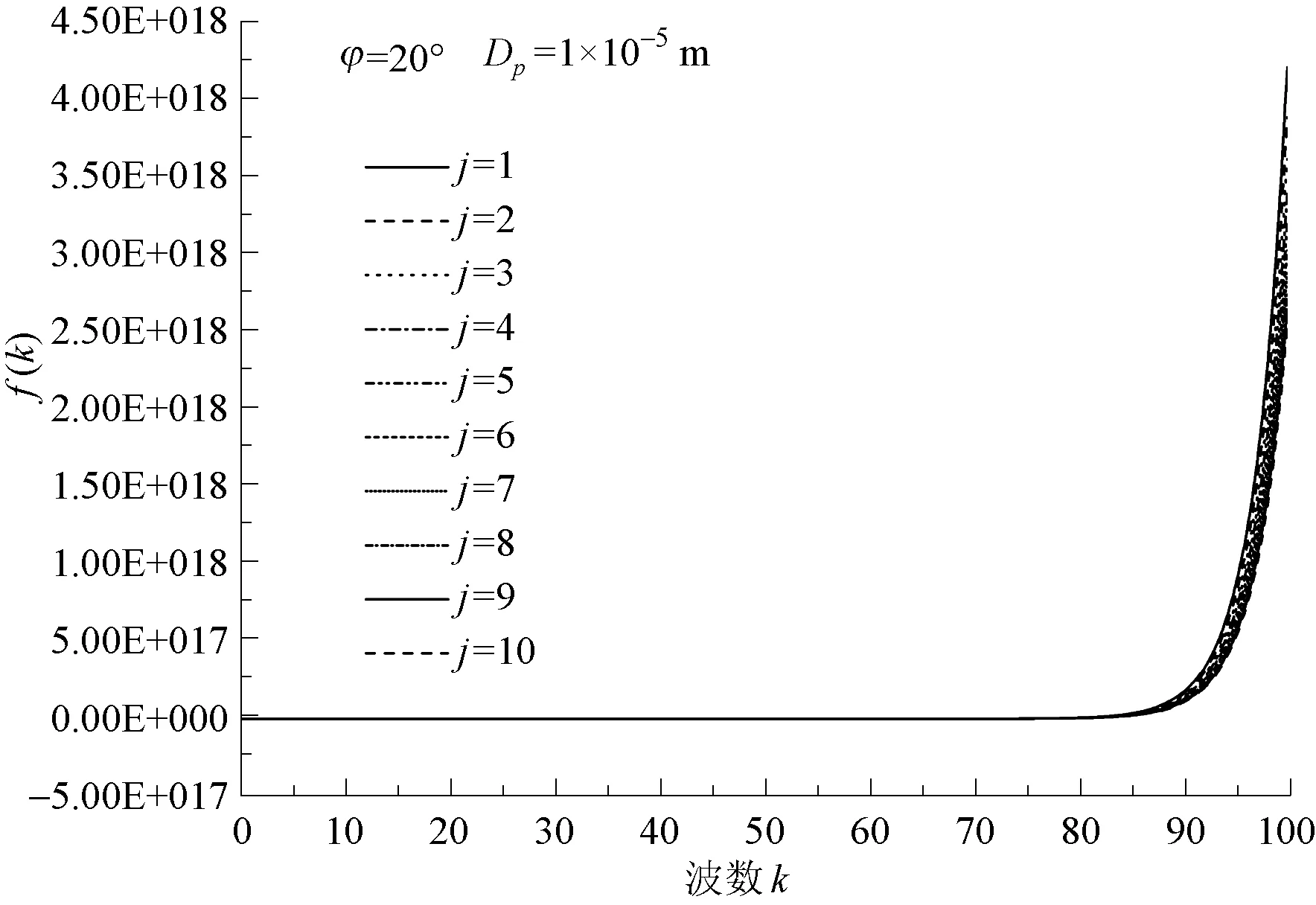
圖4 無離心力作用下的f(k)Fig.4 f(k)without Effect of Centrifugal Force

從理論模型[式(24)]中可以看出，旋轉流場下離心力包括液膜的離心力和氣相的離心力，這兩種離心力各自對界面的穩定性起著何種作用還需分別進行討論。因此，在維持其他參數不變的條件下逐漸改變各相流體的旋轉流速，計算各旋轉流速下的界面穩定性。具體的計算參數見表3所示，在圖5和圖6給出了第5段液膜的計算結果。從圖5中可以看出，當氣相角速度恒定時，液膜的穩定性隨著液膜切向旋轉流速的減小逐漸由穩定狀態過渡到不穩定狀態，即界面隨著液膜離心力的減小趨于不穩定。由此可知液膜的離心力能夠抑制液膜界面不穩定性的發展。從圖6中可以看出，當液膜切向旋轉流速恒定時，隨著氣相旋轉角速度的增加，液膜逐漸由穩定狀態過渡到不穩定狀態。即界面隨著氣相離心力的增大趨于不穩定狀態。由此可知氣相的離心力對液膜界面起著致失穩的作用。

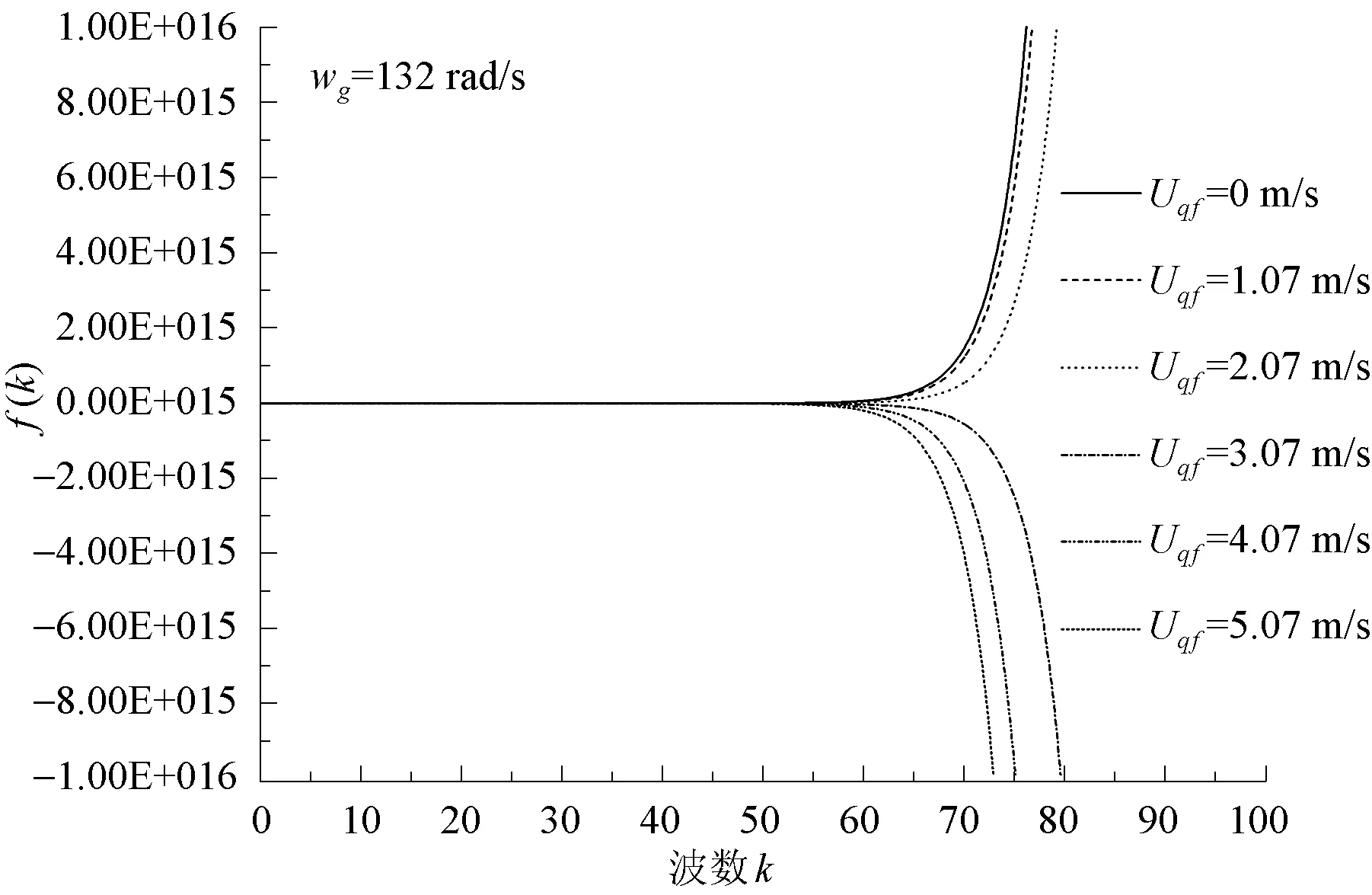
圖5 不同液膜切向流速下的界面穩定性Fig.5 Interface stability under different tangential velocity of film

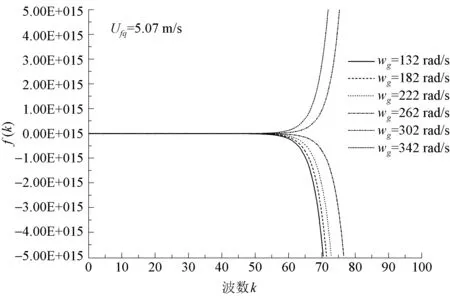
圖6 不同氣相角速度下的界面穩定性Fig.6 Interface stability under different tangential velocity of steam

結合圖3至圖6可以得出，在旋葉式分離器筒壁，液膜離心力對液膜界面的致穩作用強于氣相離心力的致失穩作用，使得整個離心力場對筒壁液膜界面不穩定性的發展起著抑制作用。

4 結論

本研究對無黏條件下旋葉式汽水分離器內部液膜界面穩定性進行了理論分析，建立了旋轉流場及無黏條件下液膜界面波的色散方程和相應的理論模型，并基于該理論模型編寫了計算程序，對不同離心力作用下的液膜界面穩定性進行了計算。通過對計算結果的對比分析，獲得了離心力的影響規律：

(1) 液膜離心力會約束界面波的發展，起著抑制界面不穩定的作用，而汽相離心力對界面起著致失穩的作用；

(2) 在分離器內部，液膜離心力對液膜界面的致穩作用強于氣相離心力的致失穩作用，使得整個離心力場對筒壁液膜界面不穩定性的發展起著抑制作用。

本研究可以作為分析旋葉式汽水分離器壁面液膜二次攜帶的基礎，并為后期建立旋葉式汽水分離器分離特性模型提供了理論支撐。

[1] Nikolay I. Kolev. Multiphase Flow Dynamics 4-Nuclear Thermal Hydraulics[M]. Berlin：Springer Publishing Corporation，2009：315-320.

[2] Tatterson D. F.. Rate of atomization and drop size in annular two-phase flow[D]. Urbana：University of Illinois，1975.

[3] Ishii M.，Grolmes M.. Inception criteria for droplet entrainment in two-phase concurrent film flow[J]. American Institute of Chemical Engineers Journal. 1975，21：309-318.

[4] Ishii M.，Mishima K.. Correlation for Liquid Entrainment in Annular Two-phase Flow of Low Viscous Fluid[R]. Argonne：Argonne National Laboratory Report，1981.

[5] Scriven，L. E.. Equation of motion for Newtonian surface fluids[J]. Chemistry Engineering Science，1960，12：98-108.

[6] D.Y. Hsieh. Kelvin-Helmholtz Stability and Two-phase Flow[J]. Acta Mathematical Scientia，1989，9：189-197.

[7] Daniel Joseph，Toshio Funada，Jing Wang. Potential Flows of Viscous and Viscoelastic Fluids[M]. Cambridge University Press，1999：105-109.

[8] 王竹溪，郭敦仁. 特殊函數概論[M]. 北京：北京大學出版社，2000：364-367.

[9] 徐濟鋆. 沸騰換熱和氣液兩相流[M]. 北京：原子能出版社，2001.

[10] Whalley，P.，Hewitt，G.. The correlation of liquid entrainment fraction and entrainment rate in annular two-phase flow[R]. Harwell：Atomic Energy Research Establishment，1978.

CentrifugalForceEffectonFilmInterfacialInstabilityonTheWallofCycloneSeparator

HUANGZhen，XIAOZe-jun，YANXiao，ZANYuan-feng，LIYong，YUANDe-wen

(CNNC Key Laboratory on Nuclear Reactor Thermal Hydraulics Technology，Nuclear Power Institution of China，Cheng Du，610041，China)

Theory study was performed for centrifugal force effect on film interfacial instability on the wall of cyclone separator in rotational flow in this paper. The momentum equations and continuity equations of gas-liquid fluid were linearized by substitution of potential function firstly. Then the dynamic boundary condition and kinematic boundary condition of interface were obtained base on stress analysis of film interface under inviscid condition. The dispersion relation of film interface wave was established by the combination of boundary conditions and the linearized equations. Based on dispersion relation and film motion law which was obtained by force equilibrium，the determination criterion of interfacial instability was established. A computer program was developed based on the theory model to calculate interfacial instability. It was found that centrifugal force had effect to constrain film interfacial instability on the wall of cyclone separator in rotational flow.

Centrifugal Force；Cyclone separator；Film；Interfacial Instability

2017-01-22

黃 振(1984—)，男，湖北荊門人，副研究員，工學博士，現從事反應堆熱工水力研究工作

TL334

A

0258-0918(2017)05-0761-07