一種基于新共軛梯度方法的滑動平均模型參數估計優化法

(燕山大學理學院 河北 秦皇島 066004)

一種基于新共軛梯度方法的滑動平均模型參數估計優化法

王美霞

(燕山大學理學院河北秦皇島066004)

基于非線性規劃的共軛思想，結合不同的共軛梯度法的優勢，給出新的參數標量以及搜索方向，從而提出一種改進的共軛梯度法，并給出全局收斂性的證明。考慮將模型參數估計轉換成無約束優化問題，然后利用改進的共軛梯度法來修正原始的ARMA(p,q)模型的參數估計值，從而提高模型的預測精度，并給出數值算例，來驗證改進方法的有效性。

非線性規劃；共軛梯度法；全局收斂性；ARMA(p,q)模型；參數估計

在時間序列的統計分析中，平穩時間序列是一類重要的隨機序列，最常用的就是ARMA(p,q)模型，全稱是自回歸移動平均模型，簡單記為ARMA(p,q)模型[1]是目前最常用的擬合平穩序列的模型。1927年，英國統計學家G.U.Yule首先提出自回歸(autoregressive，AR)模型[2]。 1970年，Box與Jenkins聯合發表了專著《時間序列分析：預測和控制》[3]對時間序列方法以及應用做了系統并且深入的論述。2003年，針對參數問題，熊淵博[4]提出了對ARMA(p,q)模型的參數進行分步估計的方法，此方法通過對AR(p)模型的兩次估計來達成ARMA(p,q)模型的參數估計，再利用實例證明該方法的有效性；2009年，范菁[5]針對如何提高模型的擬合精度的問題，提出了三參數共軛梯度法，該方法是在原始共軛梯度法的原理上引入參數標量來確保迭代步長不小于零；同一年，鄭彩萍[6]等人將非線性時序模型的參數估計法中融入了阻尼最小二乘法，提出了對于原始模型的參系數的改進方法，通過對t統計量的求解來驗證改進方法的有效性。

本文在現有文獻的基礎上，結合非線性規劃中的共軛思想，優化ARMA(p,q)模型中的參數估計，提出一種新的共軛梯度法：MHS-DY法。

一、MHS-DY法

(一)共軛梯度法

對于無約束優化問題

minf(x),x∈Rn

(1)

函數f:Rn→R1是連續可微的。

共軛梯度法是介于最速下降法與牛頓法之間的一種方法，不僅避免了最速下降法收斂速度慢的缺點，還克服了牛頓法求海賽矩陣的不足，還具有二次終止性，因此在求解上述無約束優化問題時，共軛梯度法更為合適，此方法尤其適合求解維數n較大的問題。主要迭代格式如下所示：

xk+1=xk+αkdk

(2)

其中，αk為步長因子。dk為下降搜索方向。βk為標量，標量參數不同產生的共軛梯度法不同。 常見的共軛梯度法算法有：FR算法，DY算法，HS算法，PRP算法。其中，FR算法與DY算法收斂性較好，但是數值表現并沒有HS和PRP算法好，文獻[5]提出使參數的標量滿足：

(3)

將該方法記為MHS算法，本文將結合MHS算法以及DY算法的優越之處構造出一種新的組合優化方法即MHS-DY法。

(二)MHS-DY法

針對前文中提到的無約束優化問題(1)，引用文獻[5]中提到的含參數的共軛梯度法思想，公式(3)作為參數標量，再結合DY算法的全局收斂性優勢，提出MHS-DY法：

(4)

其中

保證搜索方向為下降方向，綜合考慮搜索方向：

(5)

式中，dk滿足下降方向，并且不依賴任何線搜索。

二、基于新MHS-DY法的模型參數優化算法

(一)目標函數的確定

ARMA(p,q)模型結構為：

Xt-φ1Xt-1-...-φpXt-p=εt-θ1εt-1-...-θqεt-q

移項

Xt=φ1Xt-1+…+φpXt-p+εt-θ1εt-1-…-θqεt-q

記為

其中

ω=[φ1，φ2，…φp,-θ1,-θ2,…-θq]T

考慮到ARMA(p,q)模型中Xt與ω之間是非線性關系，定義目標函數為模型的殘差平方和：

(6)

由無約束優化理論的數學模型得知，估計模型的參數ω的問題就轉變成求使得S(ω)達到極小值的最優解ω*。

(二)初值的確定

本文采取的是AP(p0)長自回歸模型，其計算原理是：以模型的等價系統傳遞函數為入手點，同時將逆函數的概念加入其中，并運用待定系數法得到如下公式：

(7)

(8)

(9)

(三)參數估計步驟

1)對于ARMA(p,q)模型，令p+q=m，參數初值結構如下：

(10)

(11)

其中，

(12)

(13)

記為矩陣形式如下：

(14)

因此S0=S(ω0)，初始搜索方向d0=-g0，令k=0。

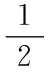
3)如果‖gk+1‖<ε，那么ωk+1就是極小值點，否則，進行下一步。

4)若k=p，則ω0=ωk+1,S0=Sk+1,g0=gk+1,d0=-g0,k=0，然后轉向2)；否則，轉向5)。

6)若(dk+1)Tgk+1≥0，則重復操作4)，轉向2)；否則，k=k+1，轉向2)。

三、收斂性分析

假設：(1)水平集Ω={∈Rn|f(x)≤f(x0)}有界。

(2)函數f在Ω的某個鄰域Φ內連續可微，并且g(x)滿足利普希茨連續條件，即?L>0，使得下式成立：

‖g(x1)-g(x2)‖≤L‖x1-x2‖,?x1,x2∈Φ

(15)

(16)

用反證法證明上述定理如下：

證明：假設結論不成立。已知?k>0,?ε>0,ε為常數，使(17)式成立

‖lk‖≥ε

(17)

由

(18)

(19)

由此得出：

(20)

四、實例分析

MHS-DY算法經數值算例證實其在求解無約束問題時同樣保持了良好的數值結果及收斂性，可將ARMA(p,q)模型的參數優化問題轉換成無約束優化問題進一步求解，本文引用文獻[5]中的算例(數據如表1所示)進一步檢驗本文算法的實用性。前100個數據用于模型的預測，101～103用于模型檢驗，利用MHS-DY算法對ARMA(1,1)模型進行參數估計，此時，初值β0=(1,0.5)，令δ=0.01，σ=0.1，同時利用Matlab[12]軟件做編程，經過五次迭代后結果如下：

ω5=(0.8673,0.4898)T

模型結構為：

xt=0.8673xt-1+εt-0.4898εt-1

利用MHS-DY算法改進后的參數模型預測結果見表2

表1 平穩序列

表2 預測結果對比

注：n 的值表示平穩序列中第n個數。

五、結論

本文的核心思想是將模型的參數估計問題轉換成無約束優化問題進行研究，參考文獻[5]的思想上提出了一種新的共軛梯度法MHS-DY算法并運用該算法優化ARMA(p,q)模型參數，詳細的證明了此方法具有全局收斂性以及充分下降性。最后，用實例進行驗證分析，結果表明優化后的模型有更好的擬合效果。

[1]王燕.應用時間序列分析[M].北京:中國人民大學出版社,2005.145-147.

[2]S.Andreas.Weigend and A.Neil Gershenfeld.Time Series Prediction:Forecasting the future and Understanding the Past,eds.Reading,MA:Addison-Welsley,1993

[3]G.E.P.Box,G.N.Jenkins and G.C.Reinsel著.時間序列分析預測與控制.顧嵐主譯.北京:中國統計出版社,1997:45-49

[4]ARMA模型參數的分步估計方法[J].湖南大學學報(自然科學版),2003,30(2):12-13.

[5]范菁.ARMA模型的兩種共軛梯度參數估計法及ARIMAX模型的應用[D].燕山大學,2009.

王美霞(1991-)，女，漢族，河北唐山人，碩士，燕山大學，最優化理論。

)