基于分形導數對非牛頓流體層流的數值研究1)

蘇祥龍 許文祥 陳 文

(河海大學力學與材料學院軟物質力學研究所，南京211100)

流體力學

基于分形導數對非牛頓流體層流的數值研究1)

蘇祥龍 許文祥 陳 文2)

(河海大學力學與材料學院軟物質力學研究所，南京211100)

非牛頓流體具有復雜的流變特性，揭示該流變特性可以更加合理地指導非牛頓流體在工農業生產中的應用.經典的非牛頓流體本構模型往往形式復雜，僅能應用于某些特定的情況.分數階導數模型具有參數少和形式簡單的特點，已成功地應用于描述非牛頓流體的運動.Hausdor ff分形導數作為一個備選的建模方法，相比分數階導數具有更簡單的形式以及更高的計算效率.本文基于Hausdor ff分形導數改進現有牛頓黏性模型，提出分形黏壺模型.通過研究分形黏壺在常應變率下表觀黏度的變化情況，以及在加、卸載條件下的蠕變及恢復特性，發現分形黏壺模型適合于描述具有黏彈性的非牛頓流體(本文稱之為分形流體).結合連續性方程及運動微分方程，推導出分形流體在平行板間層流的基本方程.按是否拖動上板和是否存在水平的壓力梯度分為3種工況，分別用數值方法計算這3種工況下流速在板間的分布及其隨時間變化的情況.通過分析不同工況下的流速分布，發現水平的壓力梯度會改變流速隨時間變化的形狀，且會推遲流速到達穩定的時間.在水平壓力梯度不存在的情況下，不同階數的分形流體具有相同的流速分布或是演變過程.另外，在水平壓力梯度存在的情況下，上板速度不影響不同階數分形流體間穩定速度的差值.

分形導數，非牛頓流體，分形流體，層流，表觀黏度

引言

非牛頓流體廣泛地存在于食品工業，醫學，石油工業等領域.不同于牛頓流體，非牛頓流體展現出復雜的流變現象，包括蠕變、時間依賴和剪切依賴的黏性.黏性依賴于剪切率的現象在實際生活中非常常見，比如玉米淀粉的懸浮液，奶油，番茄醬，冰和血液.參照牛頓流體，定義非牛頓流體的切應力與應變率之比為其表觀黏度[1]，它通常是應變率的函數.這種模型被稱為廣義牛頓模型[2]，其表達式為[3]

式中，T是偏應力張量，μ是表觀黏度函數;D是應變率張量，D=0.5h▽V+(▽V)Ti,其中，V 是速度向量，▽V是速度梯度，上標“T”表示轉置；Π是應變率張量D的不變量，Π=2tr(D2)，其中符號“tr”表示張量的跡，即主對角元素求和.冪律模型作為廣義牛頓模型的一個特例，其表觀黏度函數的表達式為[3]

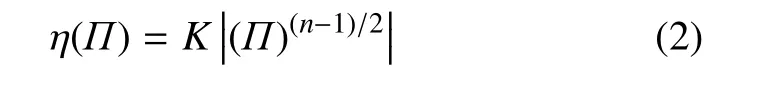
其中，K為流體的稠度系數，n是材料參數.當n=1時冪律模型退化為牛頓黏性模型，而n＞1,n＜1分別可以描述剪切增稠和剪切變稀的流體[3].另外，Oldroyd模型和Carreau模型[3]是根據表觀黏度在應變率趨于零和趨于無窮時的極限值而寫出的本構關系的表達式.如果流體存在屈服應力，且超過屈服應力之后應力與應變呈線性關系，可以用Bingham模型[4]來描述.而Herschel-Bulkley模型[5]和Casson模型[6]可以描述屈服應力之上應力與應變呈非線性關系的情況.另一方面，時間依賴的黏性也普遍存在.比如酸奶，水基氧化鐵凝膠和一些泥土，它們的黏性隨時間減小，稱為觸變性[7].而另外一些流體，像打印機油墨，滑膜液黏性卻是隨時間增加，稱為震凝性[8].有關非牛頓流體的觸變性和震凝性的本構模型研究見參考文獻[9-11].

另外，關于非牛頓流體流動特性的研究也很多.范椿[12]研究了對于二維擾動非牛頓冪律流體在重力作用下沿傾斜面流動的穩定性,得到臨界雷諾數作為冪律指數 n和平板斜率 β的函數.韓式方等[13]研究了上隨體Maxwell流體在圓管內非定常流動規律.董波等[14]基于插值補充格子波爾茲曼方法模擬了冪律流體的圓柱繞流問題.Hayat等[15]推導了Oldroyd-B流體的一些簡單流動的精確解，包括在無限大平行板間的流動.近年來，分數階導數作為一種優秀的數學建模工具，成功地應用到粘彈性建模領域[1619].另外，分數階本構方程也被用于描述非牛頓流體的運動[2022]，包括求解非牛頓流體流動的精確解[2326].然而，在數值計算時分數階微積分算子的全局性特征要求相當大的計算成本和存儲空間[27].

陳文[28]基于時空變換首次提出了Hausdor ff分形導數，與分數階導數模型相比，Hausdor ff分形導數簡單的數學定義不僅給理論推導帶來了便利，也為計算模擬節約了大量成本.目前Hausdor ff分形導數已成功地應用于反常擴散[2830]、松弛振動[31]、熱控制[32]等領域.蔡偉等[27]首次將Hausdor ff分形導數應用到黏彈性建模中，推導了分形Maxwell和分形Kelvin模型的蠕變柔量和松弛模量，數值結果表明這些模型可以很好地描述黏彈性行為.蘇祥龍等[33]將Hausdor ff分形導數用于描述非牛頓流體的流變行為，研究表明分形導數模型適宜描述非牛頓流體的剪切依賴和時間依賴的表觀黏度以及蠕變等流變現象.

本文用Hausdor ff分形導數替換牛頓黏性模型里的常規導數，得到一種描述非牛頓流體的分形黏壺模型.研究了分形黏壺在常應變率下的應力響應以及蠕變和回復特性.并在此基礎上推導了分形流體在平行板層流情況下的控制方程.用數值方法計算了多種工況下板間流速分布以及演變過程.并探究了上板的速度、水平壓力梯度以及分形導數的階數對流速分布及演變的影響.

1 Hausdor ff分形導數及其性質

基于時空尺度變換，陳文[28]提出了一種新的導數——Hausdor ff分形導數.函數 f(t)在時間方向上的Hausdor ff分形導數定義為

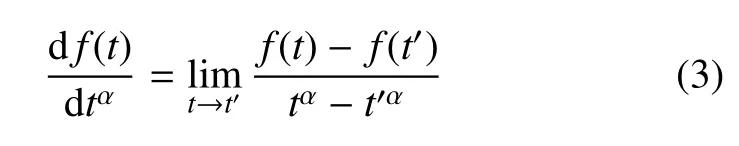
式中，d/dtα是時間分形導數算子，α是分形導數的階數，它代表一種分形量度[28]；t和t′分別代表不同的時刻.在分形不變量及分形平衡的假設下，運用變量替換=tα，可將分形導數轉化為常規導數[28].

若函數 f(t)在定義域內一階可導，且t1?α/α不為零，那么Hausdor ff分形導數與常規導數有如下關系[27]

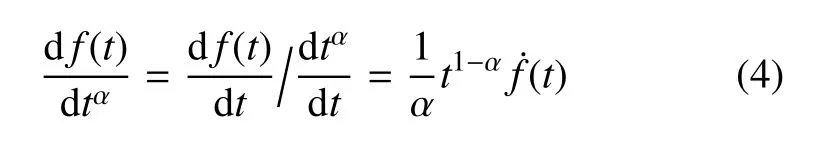
設函數 f(t)和g(t)在定義域內一階可導，g(t)≠0，且各自的α階分形導數存在，在這種情況下我們可以推導出Hausdor ff分形導數的四則運算法則：

(1)函數和差的分形導數

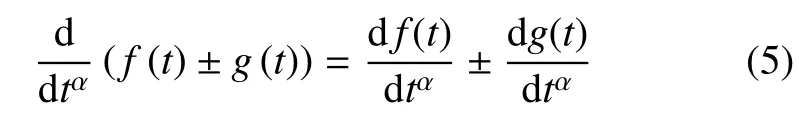
(2)函數乘積的分形導數

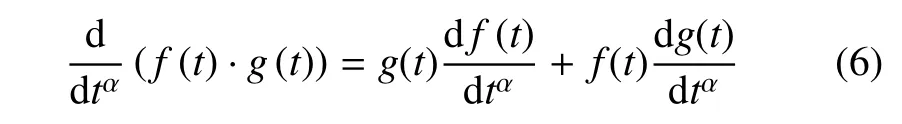
(3)函數商的分形導數

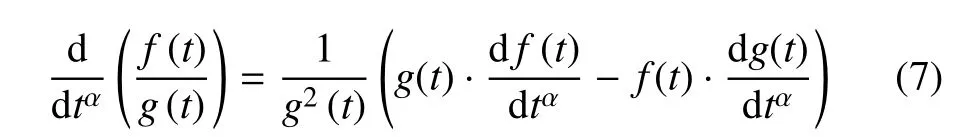
可以看到，Hausdor ff分形導數的四則運算法則與常規導數的四則運算法則一致.

2 分形黏壺模型

本文用Hausdor ff分形導數取代牛頓黏性模型里的常規導數,得到一種新的本構模型，稱其為分形黏壺模型，其本構關系為

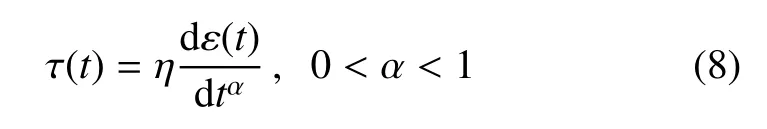
其中，τ和ε分別表示剪切應力與應變，η是材料參數.α為無量綱數，文獻[27]給出了基于分形黏壺與彈簧的串并聯模型得到的分形Maxwell模型，分形Kelvin模型和分形Zener模型，這些模型成功地描述了軟土、凍土、鹽巖以及混凝土等材料的蠕變現象.

為了更清楚地認識分形黏壺的性質，本文研究：(1)分形黏壺的表觀黏度隨時間的變化；(2)分形黏壺的蠕變及恢復特性.

2.1 表觀黏度隨時間變化

令應變率為常數c，即ε(t)=ct，代入式(8)得到應力隨時間的變化關系為

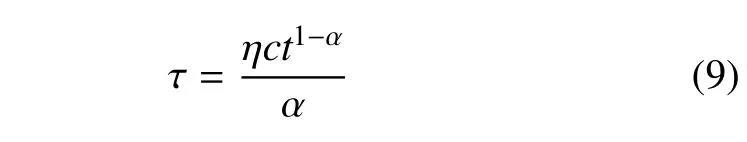
那么這種情況下分形黏壺的表觀黏度ηb可表示為

令 η =1kg·m?1·sα?2，在 α 分別取 0.3,0.5 和 0.7 時畫出分形黏壺的表觀黏度隨時間的變化情況，見圖1.從圖1可以看到，分形黏壺的表觀黏度隨時間逐漸增大；階數越大，則表觀黏度越小，且其增長速率越小.當α趨近于1時，表觀黏度幾乎維持穩定.由分形導數的定義式(3)，令α→1，那么分形導數即退化為常規導數，應變函數ε(t)的α階分形導數則退化為ε(t)的一階導數，即應變率函數˙ε(t)

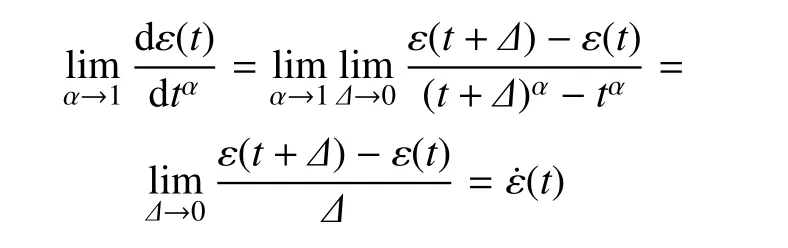
考慮上式的變換，則當α→1時，分形黏壺模型退化為牛頓黏性模型

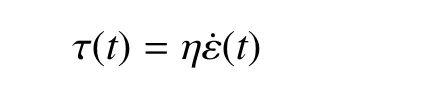
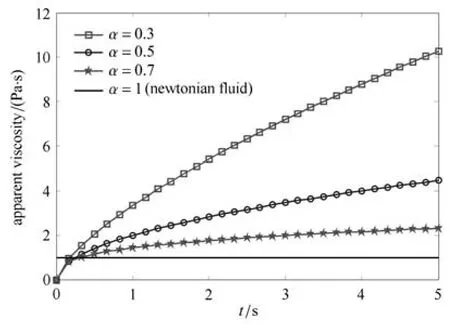
圖1 分形黏壺在常應變率下的表觀黏度Fig.1 The apparent viscosity of the fractal dashpot under constant strain rate

2.2 加、卸載時的蠕變及恢復特性

令τ(t)=τ0，代入式(8)中得到分形黏壺的蠕變響應為

選擇如圖2所示的加載路徑，在t1=1s時刻加上應力τ0，在t2=2s時刻將應力撤掉，得到分形黏壺蠕變及恢復曲線如圖3.

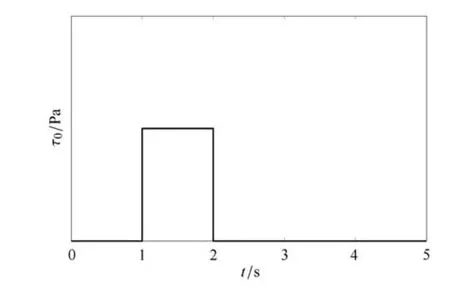
圖2 分形黏壺加載及卸載圖Fig.2 The loading and unloading for the fractal dashpot

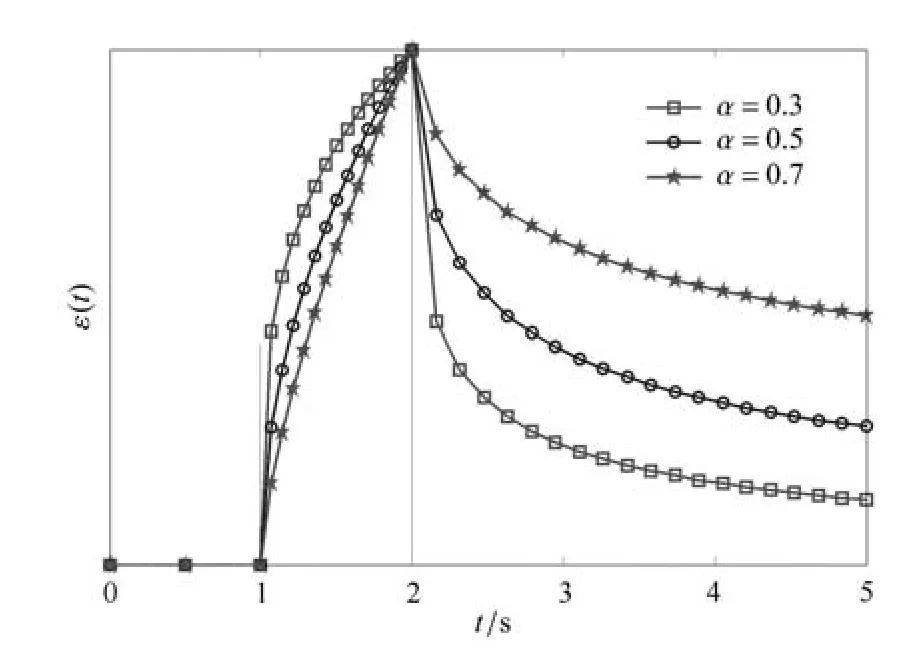
圖3 分形黏壺在不同階數下的蠕變及恢復曲線Fig.3 The creep and recovery curves of the fractal dashpot

從圖3可以看到，分形黏壺具有明顯的黏彈性.其中，當α較小時，分形黏壺蠕變及恢復變形發展較快，展現出高彈性.另外，在α比較大的情況下，蠕變變形幾乎與時間呈線性關系而恢復變形發展很慢，這種性質表現跟黏性流體很類似.由分析可知，分形黏壺的黏彈性與階數α的取值密切相關.

另一方面，從非牛頓流體的角度來說，分形黏壺可以描述表觀黏度隨時間增大的流體.而且分形黏壺的階數α取值越大，表觀黏度越小.

3 分形流體平行板層流的基本方程

為了探究分形流體的流動特點，設置一個簡單流動.如圖4所示，兩無限寬的平行剛性板水平放置在分形流體中，已知平行板間距為a，分形流體的密度為ρ，下板固定.

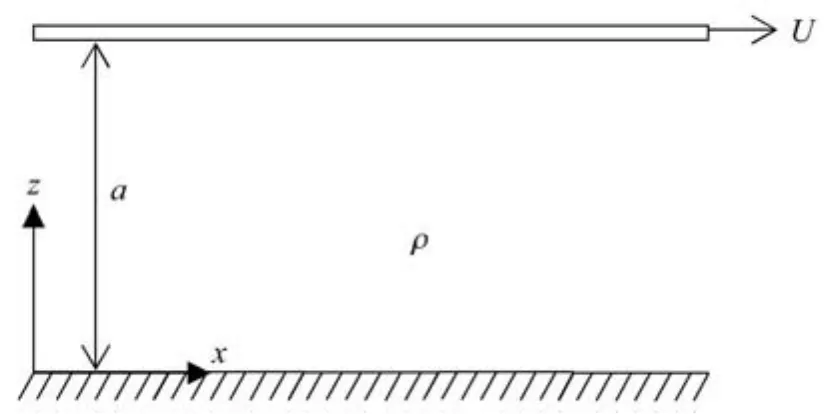
圖4 兩平行板間分形流體的層流運動Fig.4 The laminar fl ow of the fractal fl uid between two parallel plates

將滿足式(8)的具有黏彈性的非牛頓流體稱為分形流體，考慮分形流體是不可壓縮、各向同性的，那么分形流體的本構關系可以寫成如下形式

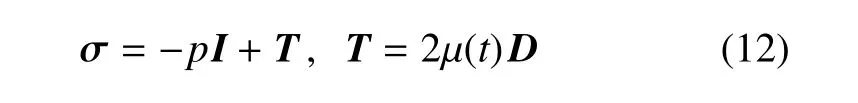
其中，σ是柯西應力張量，T是偏應力張量，D是應變率張量，I是單位張量，p表示壓力，μ是表觀黏度函數，具體寫作

考慮分形流體是不可壓縮的，其連續性方程為

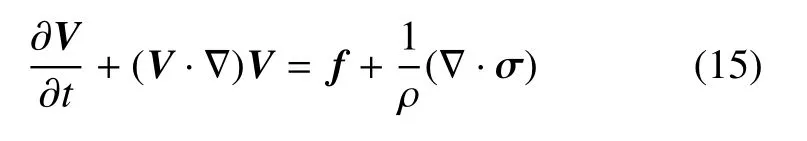
其中f是單位質量力矢量，ρ是密度.

對于分形流體在如圖4所示的平行板間的層流運動，速度矢量、應力張量只在x方向上的分量不為零，且是z和t的函數；單位質量力矢量僅有z方向上的重力項，記作

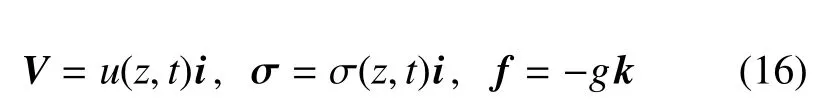
其中，u表示速度矢量在x方向上的分量；σ表示應力張量在x方向上的分量；g表示重力加速度，負號表示與圖4中指示的坐標軸正方向相反.根據上式，結合式(12)～式(14)，簡化分形流體的運動微分方程式(15)得

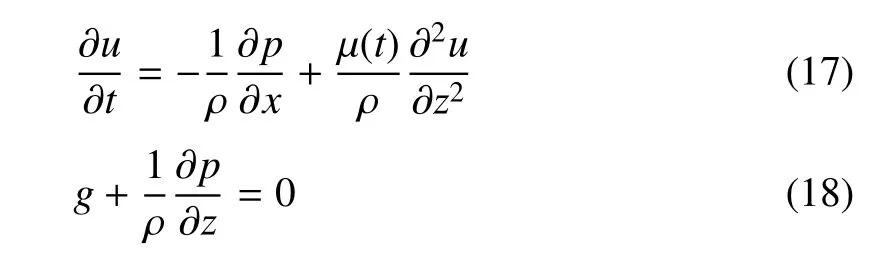
對式(18)積分得

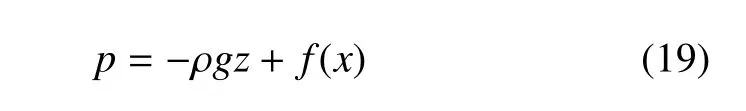
其中，f(x)是關于x的任意函數.可知?p/?x僅是x的函數，而u不是x的函數，所以求解u時?p/?x可做常數處理.將式(13)代入式(17)中，即得到分形流體平行板層流的基本方程

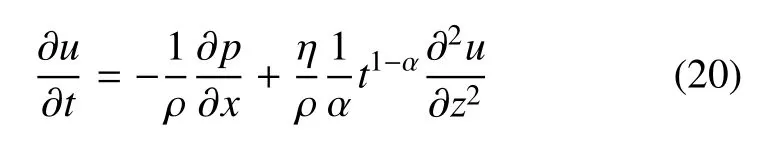
這是一個變系數的二階線性非齊次偏微分方程，本文采用軟件MATLAB中的pdetool工具箱求解.另外，牛頓流體在平行板間層流的穩定精確解為[34]

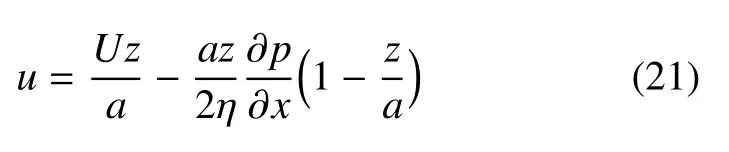
4 計算結果及討論

根據上板是否存在初始速度以及是否存在沿x方向的壓力梯度，分別在3種工況下研究分形流體在平行板間層流的流速分布及變化規律.

采用pdetool計算時，為計算方便，取a=1m,ρ =1kg/m3,η =1kg·m?1·sα?1，并取計算時間為 3s，時間和空間上分別用30個網格點劃分.

對比式(13)和式(10)可知，平行板層流情況下分形流體的表觀黏度函數與常應變率下的表觀黏度函數一致.初始時刻分形流體的表觀黏度為零，且隨時間以冪函數形式增長.對于不同的階數α，階數越大，表觀黏度函數反而越小.具體變化情況見圖1.

工況1：存在水平壓力梯度且只拖動上板

在此工況下，可以給出分形流體流動的初邊值條件為

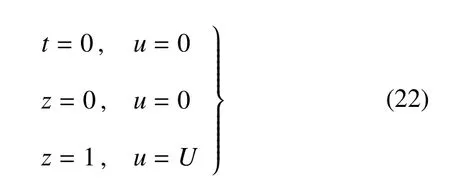
令U=1m/s,?p/?x= ?1Pa/m，當 α 取 0.3,0.5,0.7時分別計算流速.當α=0.3時求解得到的流速在板間的分布以及隨時間的變化，見圖5.

由圖5可知，從下板(z=0)到上板(z=1m)流速由0變化到1m/s，在板拖動的初始時刻，板間流速分布變化較為劇烈，隨著時間的推移，流速分布趨于平穩.

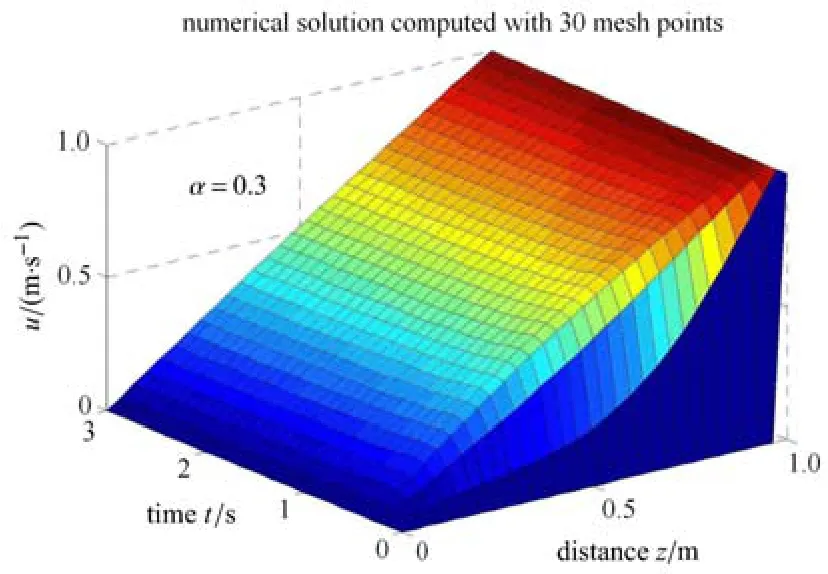
圖5 當U=1m/s,?p/?x=?1Pa/m時分形流體的流速分布及隨時間變化(α=0.3)Fig.5 The distribution and evolution of velocity of fractal fl uid for U=1m/s,?p/?x= ?1Pa/m(α =0.3)

由圖1或是式(13)可知，分形流體的表觀黏度隨階數α增大而減小，且隨時間延長.若分形流體的表觀黏度影響其流速的分布，那么兩板間的流速分布永遠不可能達到真正的穩定狀態.但表觀黏度的變化率卻是逐漸減小的

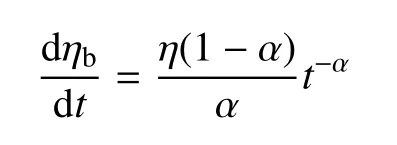
從圖5的流速分布圖也可以看出，相比于初始時刻，流速在t=3s時刻變化已經非常小了.以圖6為例，在t為0～0.5s階段，流速從0增加到0.56m/s，平均增長率為1.12m/s2；而在t為2.5～3s階段，流速從0.5198m/s降到0.5174m/s，平均減少速率為4.8×10?3m/s2.前后兩時間段流速的平均變化率相差了近200倍！因此，將t=3s時刻近似穩定的流速作為考察量，稱其為“穩定流速”.

如圖7給出了當α分別取0.3,0.5和0.7時分形流體板間穩定流速的分布以及由式(21)得到的牛頓流體的經典的穩定流速分布.從圖7可知，流速在板間以類拋物線形式分布，且下板速度為0，上板速度為1m/s.分形流體的階數α越大，即表觀黏度越小，其穩定流速也越大，且越接近于(低于)經典流速分布.

圖6給出了z=0.5m(板間中間點)處的分形流體的流速隨時間的變化曲線.由圖可知，流速從零增大到一個極大值，之后衰減并趨于穩定，清晰地再現了分形流體在平行板間流動的啟動及穩定過程.且分形流體的表觀黏度越小，對應的流速值越大.

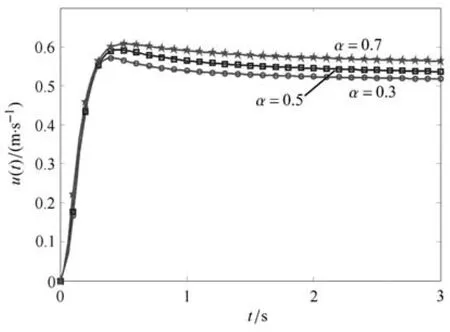
圖6 當U=1m/s,?p/?x=?1Pa/m時分形流體在z=0.5m處的流速隨時間變化圖Fig.6 The evolution of velocity of fractal fl uid on z=0.5m for U=1m/s,?p/?x= ?1Pa/m

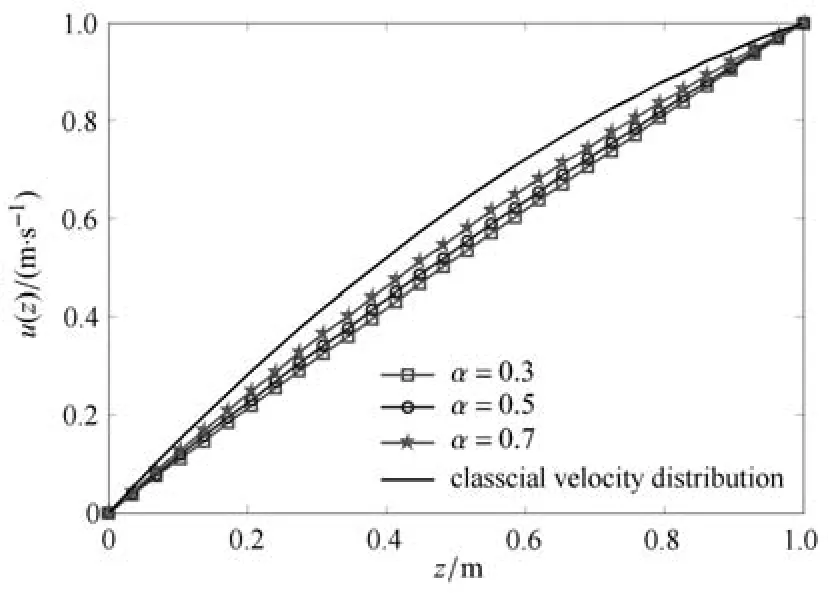
圖7 當U=1m/s,?p/?x=?1Pa/m時分形流體的穩定流速分布(t=3s)Fig.7 The stable velocity distribution(t=3s)of fractal fl uid for U=1m/s,?p/?x= ?1Pa/m

工況2：存在水平壓力梯度且上、下板固定

在此工況下，可以給出分形流體流動的初邊值條件為

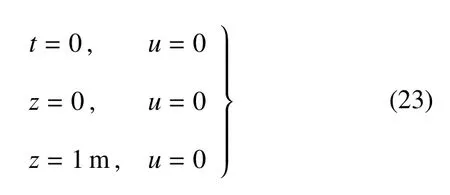
令?p/?x=?1Pa/m，在α取0.3,0.5,0.7時分別計算分形流體的流速.圖8給出了α取0.3時分形流體的流速分布及變化情況，可以發現，流速值明顯比工況1下的小.

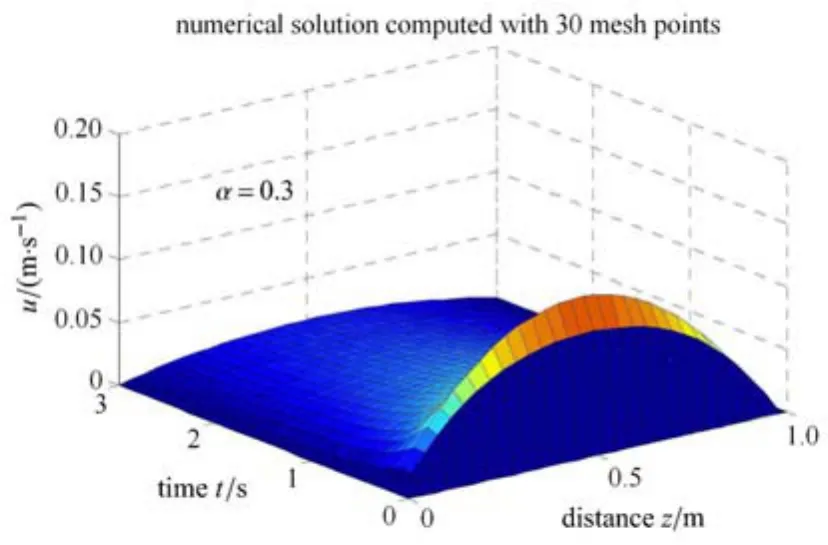
圖8 當U=0,?p/?x=?1Pa/m時分形流體的流速分布及隨時間變化圖(α=0.3)Fig.8 The distribution and evolution of velocity of fractal fl uid for U=0,?p/?x= ?1Pa/m(α =0.3)

圖9給出了當α分別取0.3,0.5和0.7時分形流體的穩定流速分布以及牛頓流體的經典穩定流速分布.可以看到，流速在板間是以類拋物線形式分布的，板兩端(z=0和z=1m)速度為零，最大速度在板中間取得.另外也可以看到，表觀黏度越小，分形流體達到的穩定流速越大.

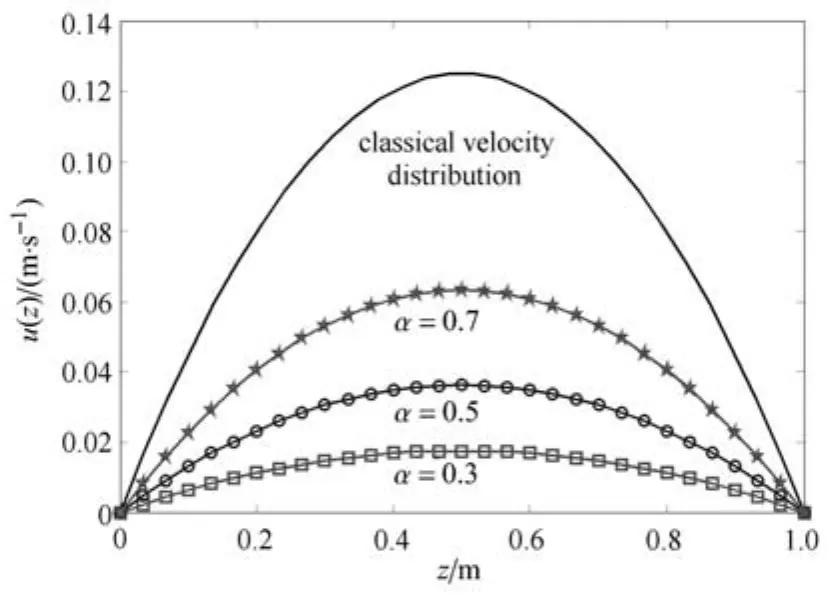
圖9 當U=0,?p/?x=?1Pa/m時分形流體的穩定流速分布(t=3s)Fig.9 The stable velocity distribution(t=3s)of fractal fl uid for U=0,?p/?x= ?1Pa/m

另外，圖10給出了z=0.5m(板中間點)處的流速隨時間的變化曲線.從圖中可以看出，流速在一個短時間內增加到極大值，隨后逐漸衰減并趨于穩定.

對比工況1，雖然兩種情況下流速值相差較大，但是對于不同階數的分形流體它們的穩定流速的差值沒有太大變化.比如在工況1的板中間點處,α=0.3和α=0.7兩種分形流體穩定流速相差大概0.05m/s(圖6或圖7)，工況2下兩種分形流體穩定流速同樣相差0.05m/s左右(圖9或圖10).說明上板的速度對不同分形流體間相對速度大小沒有影響.另外，對比圖10與圖6，發現拖動上板會縮短流速達到穩定的時間.

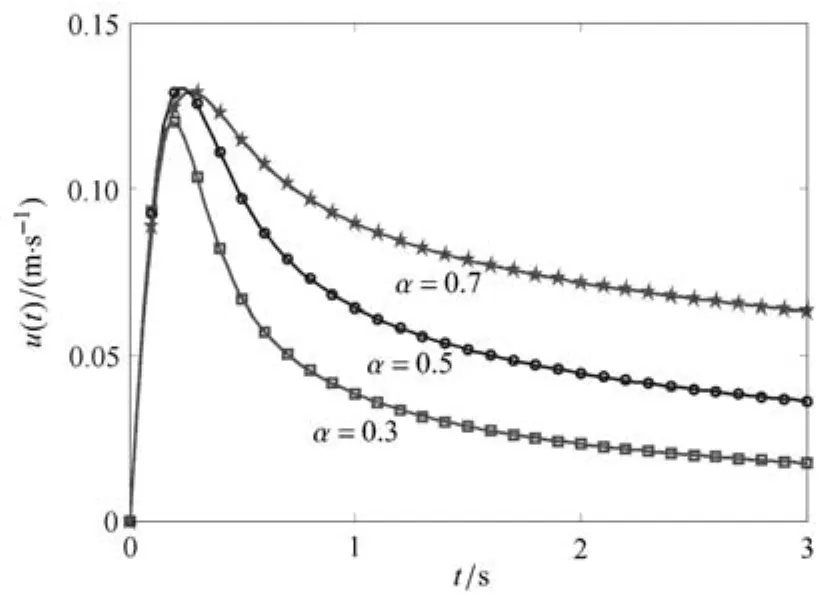
圖10 當U=0,?p/?x=?1Pa/m時分形流體在z=0.5m處的流速隨時間變化圖Fig.10 The evolution of velocity of fractal fl uid on z=0.5m for U=0,?p/?x= ?1Pa/m

工況3：不存在水平壓力梯度且只拖動上板

在此工況下，可以給出分形流體流動的初邊值條件為

令 U=1m/s,?p/?x=0，在 α 取 0.3,0.5,0.7時分別計算分形流體的流速.求解得到分形流體的流速在板間的分布以及隨時間的變化，見圖11.由圖可知，從下板(z=0)到上板(z=1m)流速由0變化到1m/s，與圖5類似.

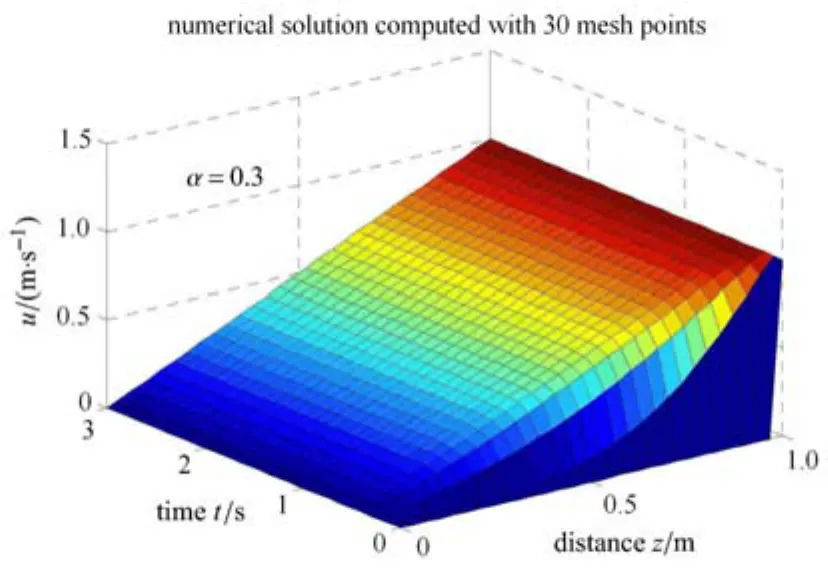
圖11 當U=1m/s,?p/?x=0時分形流體流速分布及隨時間變化圖(α=0.3)Fig.11 The distribution and evolution of velocity of fractal fl uid for U=1m/s,?p/?x=0(α =0.3)

圖12給出了當α分別取0.3,0.5和0.7時分形流體的穩定流速分布以及牛頓流體的經典穩定流速分布.可以看到，流速在板間是線性分布的.與上兩種工況不同，這種情況下不同分形流體之間流速分布相同，且與經典的流速分布重合.

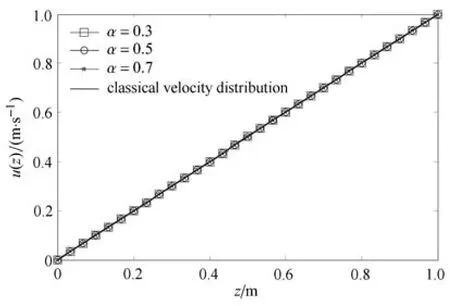
圖12 當U=1m/s,?p/?x=0時分形流體的穩定流速分布(t=3s)Fig.12 The stable velocity distribution(t=3s)of fractal fl uid for U=1m/s,?p/?x=0

由圖13可以看到，板中間位置點的流速在很短的時間內從零增加到極大值，而后直接進入穩定狀態，流速不再變化.

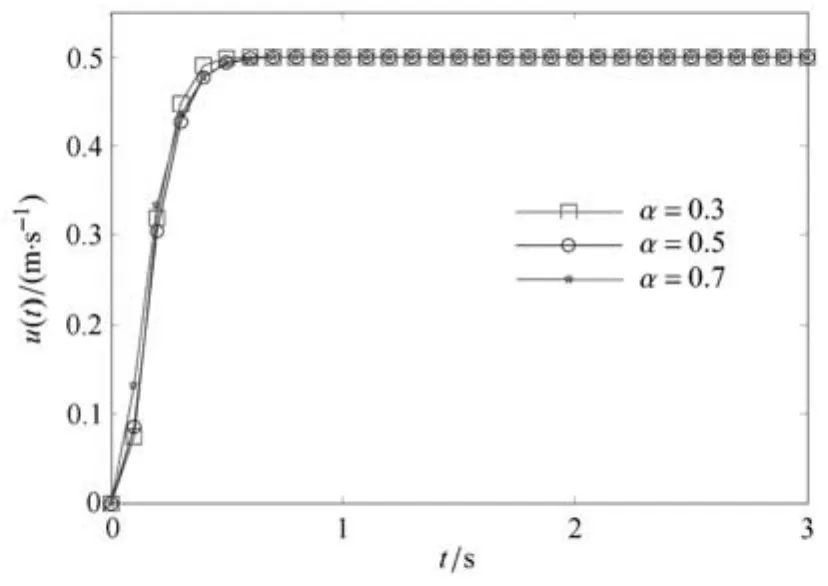
圖13 當U=1m/s,?p/?x=0時分形流體在z=0.5m處的流速隨時間變化圖Fig.13 The evolution of velocity of fractal fl uid on z=0.5m for U=1m/s,?p/?x=0

對比圖6和圖13可知，水平的壓力梯度會使流速達到一個高峰然后衰減，而無水平壓力梯度時分形流體的流速沒有衰減過程，直接到達穩定.而且水平壓力梯度的存在推遲了分形流體速度穩定的時間.另外，水平壓力梯度存在時分形流體的階數α對流速大小影響顯著，而無水平壓力梯度時流速對階數α的變化不敏感.這說明分形流體的表觀黏度只在水平壓力梯度存在時對流速分布有影響.

5 結論

(1)本文基于Hausdor ff分形導數提出了分形黏壺模型，探究了分形黏壺的力學特性.發現分形黏壺呈現出明顯的黏彈性特征，而且適合描述表觀黏度隨時間變化的非牛頓流體.結合運動方程和連續性方程，推導了分形流體在平行板層流情況下的基本方程.用數值方法計算了3種工況下分形流體在板間的流速分布以及隨時間變化的情況.

(2)計算結果顯示，流速在短時間內增加到極大值，而后隨時間衰減并趨于穩定或直接達到穩定.分形流體層流的穩定流速分布與經典的牛頓流體流速分布有類似的形狀，但都不大于經典流速值.

(3)對比3種工況發現，上板的速度會顯著影響流速的大小以及在板間的速度分布情況.而水平的壓力梯度會改變流速隨時間變化的形狀，且會推遲流速到達穩定的時間.在不存在水平壓力梯度的情況下，不同階數的分形流體具有相同的流速分布或是演變.另外，在存在水平壓力梯度的情況下，上板速度不影響不同階數分形流體間穩定速度的差值.

1 Fox RW,Mcdonald AT,Pritchard PJ,et al.Fluid Mechanics.[s.l.]:John Wiley&Sons Inc,2012

2 Galindo-Rosales FJ,Rubio-Hern′andez FJ,Sevilla A.An apparent viscosity function for shear thickening fl uids. Journal of Non-Newtonian Fluid Mechanics,2011,166(5):321-325

3 陳文芳,蔡扶時.非牛頓流體的一些本構方程.力學學報,1983,19(1):16-26(Chen Wenfang,Cai fushi.Some constitutive equations for non-Newtonian fl uid.Acta Mechanica Sinica,1983,19(1):16-26(in Chinese))

4 Bingham EC.Fluidity and Plasticity.[s.l.]:McGraw-Hill Book Co.,1922

5 Herschel W,Bulkley R.Measurement of consistency as applied to rubber-benzene solutions.Am Soc Test Proc,1926,26(2):621-633

6 Casson N.Rheology of disperse systems//Proceedings of a conference organized by the British Society of Rheology,Pergamon Press,New York,1959

7 Barnes HA.Thixotropy—areview.JournalofNon-NewtonianFluid Mechanics,1997,70(1-2):1-33

8 Oates KM,Krause WE,Jones RL,et al.Rheopexy of synovial fl uid and protein aggregation.Journal of the Royal Society Interface,2006,3(6):167-174

9 Bautista F,De Santos JM,Puig JE,et al.Understanding thixotropic and antithixotropic behavior of viscoelastic micellar solutions and liquid crystalline dispersions. I.The model. Journal of Non-Newtonian Fluid Mechanics,1999,80(2):93-113

10 Mujumdar A,Beris AN,Metzner AB.Transient phenomena in thixotropic systems.Journal of Non-Newtonian Fluid Mechanics,2002,102(2):157-178

11 Blackwell BC,Ewoldt RH.A simple thixotropic–viscoelastic constitutive model produces unique signatures in large-amplitude oscillatory shear(LAOS).Journal of Nonnewtonian Fluid Mechanics,2014,s(208-209):27-41

12 范椿.非牛頓冪律流體沿傾斜面流動的穩定性.力學學報,1982,18(2):155-160(Fan Chun.Stability of non-Newtonian power law fl uid fl owing down an inclined plane.Acta Mechanica Sinica,1982,18(2):155-160(in Chinese))

13 韓式方,伍岳慶.管內上隨體Maxwell流體非定常流動.力學學報,1990,22(5):519-525(Han Shifang,Wu Yueqing.A study on non-steady fl ow of upper-convected Maxwell fl uid in tube.Acta Mechanica Sinica,1990,22(5):519-525(in Chinese))

14 董波,李維仲,馮玉靜等.冪律流體圓柱繞流的格子波爾茲曼模擬.力學學報,2014,46(1):44-53(Dong Bo,Li Weizhong,Feng Yujing,et al.Lattice boltzmann simulation of a power-law fl uid past a circular cylinder.Acta Mechanica Sinica,2014,46(1):44-53(in Chinese))

15 Hayat T,Siddiqui AM,Asghar S.Some simple fl ows of an Oldroyd-B fl uid.International Journal of Engineering Science,2001,39(2):135-147

16 Fan W,Jiang X,Qi H.Parameter estimation for the generalized fractional element network Zener model based on the Bayesian method.Physica A:Statistical Mechanics&Its Applications,2015,427:40-49

17 Bagley RL,Torvik PJ.Fractional calculus-A di ff erent approach to the analysis of viscoelastically damped structures.AIAA Journal,2012,21(5):741-748

18 Bagley RL,Torvik PJ.On the fractional calculus model of viscoelastic behavior.Journal of Rheology,1986,30(1):133-155

19 Blair GWS.Analytical and integrative aspects of the stress-straintime problem.Journal of Scienti fi c Instruments,2002,21(5):80-84

20 Hayat T,Nadeem S,Asghar S.Periodic unidirectional fl ows of a viscoelastic fl uid with the fractional Maxwell model.Applied Mathematics&Computation,2004,151(1):153-161

21 Tan W,Xu M.Plane surface suddenly set in motion in a viscoelastic fl uid with fractional Maxwell model.Acta Mechanica Sinica,2002,18(4):342-349

22 Tripathi D.Peristaltic transport of fractional Maxwell fl uids in uniform tubes:Applications in endoscopy.Computers&Mathematics with Applications,2011,62(3):1116-1126

23 Mahmood A,Parveen S,Ara A,et al.Exact analytic solutions for the unsteady fl ow of a non-Newtonian fl uid between two cylinders with fractional derivative model.Communications in Nonlinear Science&Numerical Simulation,2009,14(7):3309-3319

24 Tong D,Wang R,Yang H.Exact solutions for the fl ow of non-Newtonian fl uid with fractional derivative in an annular pipe.Science in China Series G:Physics,Mechanics and Astronomy,2005,48(4):485-495

25 Tan W,Pan W,Xu M.A note on unsteady fl ows of a viscoelastic fl uid with the fractional Maxwell model between two parallel plates.International Journal of Non-Linear Mechanics,2003,38(5):645-650

26 Tong D,Liu Y.Exact solutions for the unsteady rotational fl ow of non-Newtonian fl uid in an annular pipe.International Journal of Engineering Science,2005,43(3):281-289

27 Cai W,Chen W,Xu W.Characterizing the creep of viscoelastic materials by fractal derivative models.International Journal of Non-Linear Mechanics,2016,87:58-63

28 Chen W.Time–space fabric underlying anomalous di ff usion.Chaos,Solitons&Fractals,2006,28(4):923-929

29 Chen W,Sun H,Zhang X,et al.Anomalous di ff usion modeling by fractal and fractional derivatives.Computers&Mathematics with Applications,2010,59(5):1754-1758

30 Liang Y,Ye AQ,Chen W,et al.A fractal derivative model for the characterization of anomalous di ff usion in magnetic resonance imaging.Communications in Nonlinear Science&Numerical Simulation,2016,39:529-537

31 Chen W,Zhang X,Koro?sak D.Investigation on fractional and fractal derivative relaxation-oscillation models.International Journal of Nonlinear Sciences&Numerical Simulation,2010,11(1):3-10

32 Reyesmarambio J,Moser F,Gana F,et al.A fractal time thermal model for predicting the surface temperature of air-cooled cylindrical Li-ion cells based on experimental measurements.Journal of Power Sources,2016,306:636-645

33 Su X,Chen W,Xu W.Characterizing the rheological behaviors of non-Newtonian fl uid via a viscoelastic component:Fractal dashpot.Advances in Mechanical Engineering,2017,9(3):1-12

34 王惠民.流體力學基礎.北京：清華大學出版社,2013(Wang Huiming.Basis of fl uid mechanics.Beijing:Tsinghua University Press,2013(in Chinese))

NUMERICAL STUDY FOR LAMINAR FLOW OF NON-NEWTONIAN FLUID BASED ON FRACTAL DERIVATIVE1)

Su Xianglong Xu Wenxiang Chen Wen2)
(Institute of Soft Matter Mechanics，College of Mechanics and Materials，Hohai University，Nanjing 211100，China)

Non-Newtonian fl uid has complex rheological characteristics.It is very helpful to reveal these characteristics for the applications of non-Newtonian fl uid in industry and agriculture.The classical rheological models of non-Newtonian fl uid usually have sophisticated forms and the limitations of speci fi c materials or rheological situations.Fractional models have been successfully applied to describe the motion of non-Newtonian fl uid due to their simplicity and few parameters.As an alternative method,the Hausdor fffractal derivative possesses simpler form and higher computational efficiency compared with the fractional derivative.This paper proposes a fractal dashpot model that improves the current Newton’s Law by using the Hausdor fffractal derivative.By investigating the apparent viscosity,the creep and recovery characteristics of the fractal dashpot,it shows that the proposed fractal dashpot model is suitable to describe the non-Newtonian fl uid with viscoelasticity(the so-called fractal fl uid).Combined the fractal dashpot model with the continuity and motion equations,the basic equation for the fractal fl uid for the laminar fl ow between two parallel plates is derived.Moreover,the velocity distributions between two plates are numerically calculated in three cases,which can be obtained through whether there is horizontal pressure gradient or the initial velocity of upper plate.It is found that the horizontal pressure gradient can change the shape of velocity over time and delay the arrival of stable velocity.The fractal fl uid with di ff erent orders has the same velocity distribution and evolution when the horizontal pressure gradient doesn’t exist.In addition,the velocity of upper plate doesn’t in fl uence the di ff erence of stable velocity between di ff erent orders of fractal fl uid when the horizontal pressure gradient exists.

fractal derivative,non-Newtonian fl uid,fractal fl uid,laminar fl ow,apparent viscosity

O373

A

10.6052/0459-1879-16-318

2016–11–07收稿，2017–07–17 錄用,2017–07–19 網絡版發表.

1)國家自然科學基金(11372097,11402076,11572111)，江蘇省自然科學基金(BK20130841)和“111”計劃(B12032)資助項目.2)陳文，教授，主要研究方向：分數階及分形導數對軟物質建模,無網格方法研究.E-mail：chenwen@hhu.edu.cn

蘇祥龍,許文祥,陳文.基于分形導數對非牛頓流體層流的數值研究.力學學報,2017,49(5):1020-1028

Su Xianglong,Xu Wenxiang,Chen Wen.Numerical study for laminar fl ow of non-Newtonian fl uid based on fractal derivative.Chinese Journal of Theoretical and Applied Mechanics,2017,49(5):1020-1028