由擴(kuò)張法構(gòu)造帶Novikov結(jié)構(gòu)的李代數(shù)

, ,

(上海理工大學(xué) 理學(xué)院,上海 200093)

由擴(kuò)張法構(gòu)造帶Novikov結(jié)構(gòu)的李代數(shù)

胡建華,王資敏,曾博文

(上海理工大學(xué) 理學(xué)院,上海200093)

在特征為零的數(shù)域上給出構(gòu)造李代數(shù)帶Novikov結(jié)構(gòu)的一種方法——擴(kuò)張法.利用2-上循環(huán)和李代數(shù)表示,由一個(gè)阿貝爾李代數(shù)和一個(gè)任意李代數(shù)給出了擴(kuò)張李代數(shù)的定義;帶Novikov結(jié)構(gòu)的李代數(shù)既具有仿射結(jié)構(gòu),也具有Novikov結(jié)構(gòu),恰當(dāng)定義乘積后,給出了擴(kuò)張李代數(shù)具有仿射結(jié)構(gòu)的充要條件,給出了擴(kuò)張李代數(shù)具有Novikov結(jié)構(gòu)的充要條件.此方法在實(shí)際中僅適用于一些特殊的李代數(shù),故給出了一個(gè)由擴(kuò)張法構(gòu)造帶Novikov結(jié)構(gòu)的低維李代數(shù)的實(shí)例.

2-上循環(huán); 仿射結(jié)構(gòu);Novikov結(jié)構(gòu); 擴(kuò)張

1 仿射結(jié)構(gòu)和Novikov結(jié)構(gòu)

冪零李代數(shù)[1-2]和可解李代數(shù)[1-3]是李理論中兩類重要的李代數(shù),但因其結(jié)構(gòu)的復(fù)雜性,還有很多問題有待解決,受到許多學(xué)者的關(guān)注.Novikov代數(shù)是一類應(yīng)用廣泛的代數(shù),文獻(xiàn)[4]提出了具有Novikov結(jié)構(gòu)的李代數(shù)的概念,并用來研究冪零李代數(shù)和可解李代數(shù)的結(jié)構(gòu),同時(shí)指出,并不是所有的李代數(shù)都能帶有Novikov結(jié)構(gòu).文獻(xiàn)[5]證明了任意特征為0的域上具有Novikov結(jié)構(gòu)的有限維李代數(shù)是可解的.因此,Novikov結(jié)構(gòu)在討論李代數(shù)的可解性上具有重要意義.文獻(xiàn)[6]探討了k-步可解李代數(shù)的 Novikov結(jié)構(gòu).文獻(xiàn)[7]給出了如何利用2-上循環(huán)和李代數(shù)表示構(gòu)造擴(kuò)張李代數(shù)的方法.本文將在特征為零的域上給出一種賦予擴(kuò)張李代數(shù)Novikov結(jié)構(gòu)的方法,給出了擴(kuò)張李代數(shù)具有Novikov結(jié)構(gòu)的充要條件.

定義1[1-2,8]設(shè)g是域k上的向量空間,在g中定義了一個(gè)李括號(hào)積(記為[·,·]),對(duì)?x,y∈g,有[x,y]∈g,且以下3個(gè)條件成立:

a. 李括號(hào)積是雙線性的;

b. [x,x]=0,?x∈g;

c. [x,[y,z]]+[y,[z,x]]+[z,[x,y]]=o,?x,y,z∈g(Jacobi等式).

稱g為域k上的一個(gè)李代數(shù).

由條件b易得,當(dāng)Chark≠2時(shí),有[x,y]=-[y,x],?x,y∈g.

定義2[ 5,9]設(shè)k是任意域,代數(shù)A的乘積 (x,y)x·y,若滿足等式

(1)

稱A為左對(duì)稱代數(shù).

若此乘法還滿足

(x·y)·z=(x·z)·y,?x,y,z∈A

(2)

稱A為 Novikov代數(shù).

定義3[ 5,9]設(shè)k是任意域,若李代數(shù)g上定義了左對(duì)稱乘積(x,y)x·y,且滿足

[x,y]=x·y-y·x,?x,y∈g

(3)

則稱g具有仿射結(jié)構(gòu).

若該乘積還滿足式(2),則稱g具有Novikov結(jié)構(gòu).

定義4[5,9]一個(gè)李代數(shù)g的導(dǎo)出列:g(1)=g,g(i+1)=[g(i),g(i)],i∈,若存在整數(shù)n,有g(shù)(n+1)=o,則稱g是n步可解的;一個(gè)李代數(shù)g的下中心列:g1=g,gi+1=[g,gi],i∈,若存在整數(shù)n,有g(shù)n+1=o,則稱g是n步冪零的.

性質(zhì)11步可解李代數(shù)、1步冪零李代數(shù)是阿貝爾李代數(shù).

證明由g(2)=g2=[g,g]=0,結(jié)論顯然成立.

性質(zhì)23步冪零李代數(shù)是2步可解步李代數(shù).

證明設(shè)李代數(shù)g是3步冪零的,則g(4)=[g,[g,[g,g]]]=0.由Jacobi等式,?x,y,z,w∈g,

[[x,y],[z,w]]=[x,[y,[z,w]]]+

[y,[[z,w],x]]=[x,[y,[z,w]]]-

[y,[x,[z,w]]]=0

故g(3)=[g(2),g(2)]=0,g是2步可解李代數(shù).

2 擴(kuò)張法構(gòu)造Novikov結(jié)構(gòu)

設(shè)k是特征為零的域,a是一個(gè)阿貝爾李代數(shù),b是任意李代數(shù).因?yàn)?a是阿貝爾李代數(shù),存在自然的b-模[10]結(jié)構(gòu),記為

φ:b→End(a),(x,a)φ(x)a,?x∈b,a∈a

且對(duì)所有的x,y∈b,有

φ([x,y])=φ(x)φ(y)-φ(y)φ(x)

(4)

記Ω∈Z2(b,a)表示2-上循環(huán),它是斜對(duì)稱雙線性映射Ω:b×b→a,且滿足

φ(x)Ω(y,z)-φ(y)Ω(x,z)+φ(z)Ω(x,y)=

Ω([x,y],z)-Ω([x,z],y)+Ω([y,z],x)

(5)

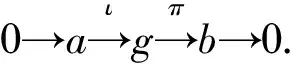
(6)

則g=a×b構(gòu)成一個(gè)李代數(shù),稱g為李代數(shù)b經(jīng)由阿貝爾李代數(shù)a擴(kuò)張的李代數(shù).

現(xiàn)在g上構(gòu)造Novikov結(jié)構(gòu).

假設(shè)g=(a,b,φ,Ω)是如上所定義的擴(kuò)張李代數(shù),且李代數(shù)a有仿射結(jié)構(gòu)(a,b)a·b,?a,b∈a,[a,b]=a·b-b·a;b有仿射結(jié)構(gòu)(x,y)x·y,?x,y∈b,[x,y]=x·y-y·x.再設(shè)ω:b×b→a是一個(gè)雙線性映射,φ1,φ2:b→End(a)是李代數(shù)表示[11].定義一個(gè)雙線性乘積g×g→g,?a,b∈a,x,y∈b,

(7)

引理1阿貝爾李代數(shù)a若有仿射結(jié)構(gòu),則a具有交換性和結(jié)合性,即

a·b=b·a;(a·b)·c=a·(b·c),?a,b,c∈a

證明因?yàn)閍是阿貝爾的,則[a,b]=a·b-b·a=0,得a·b=b·a.又因a是左對(duì)稱的,有

a·(b·c)-(a·b)·c=b·(a·c)-(b·a)·c

即a·(b·c)=b·(a·c),可得

引理2若李代數(shù)b是阿貝爾的,則g=(a,b,φ,Ω)是兩步可解李代數(shù).

證明若李代數(shù)b是阿貝爾的,由[(a,x),(b,y)]∶=(φ(x)b-φ(y)a+Ω(x,y),[x,y]),可知

g(2)=[g,g]?(a,o),g(3)=[g(2),g(2)]?(o,o)=o

定理1式(7)定義了李代數(shù)g上的一個(gè)仿射結(jié)構(gòu)[12]當(dāng)且僅當(dāng)滿足下面的條件:

a.ω(x,y)-ω(y,x)=Ω(x,y);

b.φ2(x)-φ1(x)=φ(x);

c.φ2(x)ω(y,z)-φ2(y)ω(x,z)-φ1(z)·Ω(x,y)=ω(y,x·z)-ω(x,y·z)+ω([x,y],z);

d.a·ω(y,z)+φ1(y·z)a=φ2(y)φ1(z)a-φ1(z)φ(y)a;

e.a·(φ1(z)b)=b·(φ1(z)a);

f.φ2(y)(a·c)-a·(φ2(y)c)=(φ(y)a)·c;

g.Ω(x,y)·c=0.

?a,b,c∈a,x,y,z∈b.

證明?u=(a,x),v=(b,y),w=(c,z)∈g,需證乘積 ° 滿足式(3)和式(1).由式(7)及a,b的仿射性得

由式(6),[u,v]=u°v-v°u當(dāng)且僅當(dāng)

令a=b=0,可得ω(x,y)-ω(y,x)=Ω(x,y),由此再考慮a=0的情況,得φ2(x)-φ1(x)=φ(x).又

經(jīng)計(jì)算,

又

式(1)成立當(dāng)且僅當(dāng)以上2個(gè)等式相等.令a=b=c=0,可得條件c.令a=b=0,由條件c可得條件g;令b=c=0,由條件c可得條件d;令z=x=b=0,可得條件f;令c=x=y=0,可得條件e.反之,若條件a—g成立,則有式(1)和(3)成立,得證.

定理2式(7)定義了李代數(shù)g上的一個(gè)Novikov結(jié)構(gòu)當(dāng)且僅當(dāng)乘積 ° 滿足條件a—g,且滿足條件:

h.φ1(z)ω(x,y)-φ1(y)ω(x,z)=ω(x·z,y)-ω(x·y,z);

i.ω(x,y)·c+φ2(x·y)c=φ1(y)φ2(x)c;

j. [φ1(x),φ1(y)]=0;

k. (φ2(x)b)·c=(φ2(x)c)·b;

l.φ1(z)(a·b)=(φ1(z)a)·b;

m. (x·y)·z=(x·z)·y.

證明?u=(a,x),v=(b,y),w=(c,z)∈g,需證乘積 ° 滿足式(2).

若(u°v)°w=(u°w)°v,由u,v,w的任意性,比較上兩式的右邊,令a=b=c=0,得條件h和m.令a=b=0時(shí),結(jié)合條件h,可得條件i; 令b=c=0時(shí),結(jié)合條件h,可得φ1(z)φ1(y)a=φ1(y)φ1(z)a,由a,y,z的任意性,可得條件j.令y=z=a=0,可得條件k,最后,令x=y=c=0,可得式(l).反之,若條件a—m成立,則g滿足式(1)～(3),具有Novikov結(jié)構(gòu).得證.

推論1設(shè)g=(a,b,φ,Ω),若b是阿貝爾的,且a,b上的左對(duì)稱乘積是平凡的,則式(7)在李代數(shù)g上定義一個(gè)仿射結(jié)構(gòu)當(dāng)且僅當(dāng)滿足下面的條件:

a.ω(x,y)-ω(y,x)=Ω(x,y);

b.φ2(x)-φ1(x)=φ(x);

c.φ2(x)ω(y,z)-φ2(y)ω(x,z)=φ1(z)·Ω(x,y);

d. [φ1(x),φ2(y)]=φ1(x)φ1(y).

進(jìn)一步,若式(7)在g上定義了一個(gè)Novikov結(jié)構(gòu),還需滿足條件:

e.φ1(z)ω(x,y)=φ1(y)ω(x,z);

f.φ1(x)φ2(y)=0;

g. [φ1(x),φ1(y)]=0.

證明因?yàn)?a,b上的左對(duì)稱乘積是平凡的,即a·b=x·y=0,?a,b∈a,x,y∈b.由定理1和定理2,結(jié)論顯然成立.

3 實(shí) 例

定理1和定理2給出了擴(kuò)張李代數(shù)g=(a,b,φ,Ω)具有Novikov結(jié)構(gòu)的充要條件,即找尋一系列方程的解,實(shí)際中這樣的解并不容易求出,因此,此方法在實(shí)際中只適用于一些特殊的李代數(shù).現(xiàn)僅考慮一種低維的情況.

例1設(shè)g為五維李代數(shù),其基為(a,b,c,x,y),非零李括號(hào)為

[x,y]=a,[x,a]=b,[y,a]=c

不難驗(yàn)算g是一個(gè)3步冪零李代數(shù),因此,g是2步可解的.現(xiàn)分3步在g上構(gòu)造一個(gè)Novikov結(jié)構(gòu).

a. 將g看成一個(gè)擴(kuò)張李代數(shù),取a=span{a,b,c},b=span{x,y},a,b為阿貝爾李代數(shù),令

則g=a×b=(a,b,φ,Ω)是b經(jīng)由a擴(kuò)張的李代數(shù).

b. 尋找滿足推論1中等式a—g的解φ1,φ2,ω.可假設(shè)a,b有一個(gè)平凡的左對(duì)稱乘積,只需簡(jiǎn)單驗(yàn)算,可取

c. 根據(jù)式(7)定義乘積°.因?yàn)?g=a×b,a?(a,o),b?(o,b),根據(jù)式(7),可取非零乘積

a°x=-b/2,x°a=b/2,y°a=c,y°x=-a

即可,這樣g=a×b=(a,b,φ,Ω)就具有Novikov結(jié)構(gòu).

[1] HUMPHREYS J E.Introduction to Lie algebras and representation theory[M].New York:Springer-Verlag,1972.

[2] 蘇育才,盧才輝,崔一敏.有限維半單李代數(shù)簡(jiǎn)明教程[M].北京:科學(xué)出版社,2008.

[3] DE GRAAF W A.Classification of solvable Lie algebras[J].Experimental Mathematics,2005,14(1):15-25.

[4] ZEL'MANOV E.On a class of local translation invariant Lie algebras[J].Soviet Mathematics-Doklady,1987,35:216-218.

[5] BURDE D.Classical r-matrices and Novikov algebras[J].Geometriae Dedicata,2006,122(1):145-157.

[6] BURDE D,DEKIMPE K,VERCAMMEN K.Novikov algebras and Novikov structures on Lie algebras[J].Linear Algebra and its Applications,2008,429(1):31-41.

[7] BENKART G M,MOODY R V.Derivations,central extensions,and affine Lie algebras[J].Algebras,Groups and Geometries,1986,3(4):456-492.

[8] 胡建華,趙衛(wèi)萍.一類特殊冪零李代數(shù)的結(jié)構(gòu)[J].上海理工大學(xué)學(xué)報(bào),2015,37(3):215-219.

[9] BURDE D,DEKIMPE K.Novikov structures on solvable Lie algebras[J].Journal of Geometry and Physics,2006,56(9):1837-1855.

[10] 劉紹學(xué),郭晉云,朱彬,等.環(huán)與代數(shù)[M].2版.北京:科學(xué)出版社,2009.

[11] 胡建華,劉國華.有限域上型A1的Chevalley群之間的同態(tài)[J].上海理工大學(xué)學(xué)報(bào),2009,31(4):307-310.

[12] BURDE D.Affine structures on nilmanifolds[J].International Journal of Mathematics,1996,7(5):599-616.

ConstructionofLieAlgebraswithNovikovStructureviaExtensions

HU Jianhua,WANGZimin,ZENGBowen

(CollegeofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

A method via extension was proposed to construct Lie algebra with Novikov structure over a field of characteristic zero.Using 2-cocycle and the representations of Lie algebras,the definition of extended Lie algebras was given by an Abelian Lie algebra and an arbitrary Lie algebra.A Lie algebra with Novikov structure is endowed with both affine structure and Novikov structure.With a proper product defined,the necessary and sufficient conditions for the extended Lie algebras endowed with affine structure was given.And the necessary and sufficient conditions for the extended Lie algebras endowed with Novikov structure was given.In practice the method is only suited to some special Lie algebras.An example was presented of the low-dimensional Lie algebra with the Novikov structure constructed by extension.

2-cocycle;affinestructure;Novikovstructure;extension

1007-6735(2017)05-0416-04

10.13255/j.cnki.jusst.2017.05.002

2017-03-29

上海理工大學(xué)教師教學(xué)發(fā)展研究基金資助項(xiàng)目(CFTD17015Z, CFTD17016Z)

胡建華(1978-),女,講師.研究方向:代數(shù)群及其表示理論.E-mail:smilydragon2011@163.com

O152

A

(編輯:石 瑛)