基于仿真的博弈系統優化策略研究

,

(上海理工大學 理學院,上海 200093)

基于仿真的博弈系統優化策略研究

田偉,劉懿芳

(上海理工大學 理學院,上海200093)

以石頭剪刀布博弈系統為例,提出一種新的理論方法優化該系統,目的是在不受其他因素影響下最大化玩家獲得的收益,這種新方法即凸優化.引入非零和矩陣建立凸優化算法模型,定量地創建了石頭剪刀布博弈系統收益方程,這種方法前人鮮有研究.創新地提出了博弈系統最優值的臨界方程即鞍點方程,并用強對偶理論證明了該方程的正確性.重點研究凸優化中的Newton算法對石頭剪刀布博弈系統進行數據仿真和最大化玩家獲得的收益.仿真結果表明,數值結果與理論假設相一致,驗證了該方法的可行性和正確性.該研究對于理解博弈系統和應用凸優化具有十分重要的意義.

仿真; 凸優化; 博弈系統; 鞍點

石頭剪刀布(rock-paper-scissors,RPS)作為一個基本的非合作博弈系統[1],已廣泛用于研究生物學中的競爭現象,如生態系統中物種的多樣性[2-7].納什均衡理論[8-10]在研究經典博弈論和進化博弈論中起著重要的作用,該理論假設玩家足夠理性,目的是為了確保玩家能夠了解對手的戰略,從而優化自身的策略[1,11-13].很多研究致力于在博弈系統中建立模型獲得系統最優,如石頭剪刀布博弈系統動力學模型[14-15]、無標度網絡記憶模型[16]和循環占優模型[17-19].此外,由于凸優化具有較好的可擴展性和廣泛的應用性,常用于解決電子技術[20-21]和軟件工程[22-25]等方面的優化問題.

目前,對凸優化的研究越來越受到重視,但將其應用于最優化博弈系統的研究鮮有報道.本文提出用凸優化優化博弈系統中玩家的收益,通過在凸優化模型中設定不同的值進行仿真,使系統最大收益處鞍點方程成立,從而證明凸優化的可行性,這在理論研究和實際應用中具有一定的創新性和前瞻性.

1 模 型

本文以2人非零和石頭剪刀布為例研究非合作博弈系統,系統中每個玩家進行多次回合,每輪玩家可以選擇石頭(rock,R)、剪刀(scissors,S)、布(paper,P)中的任意一個動作,如圖1所示.收益g(g>1)被定義為決定勝負的唯一參數[1],玩家根據g的大小決定選擇的動作,如圖2所示.當兩個玩家(X和Y)選擇相同的動作時,玩家X和玩家Y同時取得單位為1的收益;當玩家X擊敗玩家Y時,玩家X的收益為g,玩家Y的收益為0,反之亦然.

圖1 收益樹狀圖Fig.1 Payoff trees

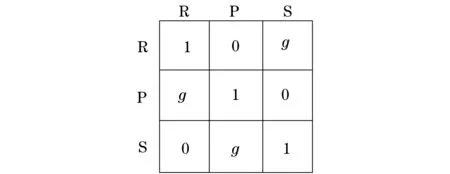
圖2 收益矩陣Fig.2 Payoff matrix

2 RPS博弈系統的凸優化

2.1凸優化方程的引入

玩家X和玩家Y每輪收益的期望值分別為

WX=XTAY

(1)

WY=YTAX

(2)

與傳統的收益方程相比,本文的收益方程是嚴格凸的.以下為凸優化問題

XR+XP+XS=1;YR+YP+YS=1

(3)

(4)

式中:玩家X的策略i∈{1,2,3};玩家Y的策略j∈{1,2,3}.

如上所述,式(1)～(4)具有凸性,因此所有最優解是全局最優解.Boyd等[26]表示凸優化是一個基本屬性,任何局部優化鞍點都是(全局)最優的.進一步假設,式(5)和式(6)嚴格可行.

2人非零和博弈系統的矩陣形式表示為YTAX+XTAY≠0.為定量研究該系統,假設玩家X先作選擇,然后玩家Y根據玩家X的選擇再作決定.玩家X想最小化收益WY,而玩家Y想最大化收益WY.同理,玩家X想最大化收益WX,而玩家Y想最小化收益WX.

玩家X最佳策略是利用變量X最小化收益YTAX

(7)

而玩家Y利用變量Y最大化收益

(8)

YRXR+YPXP+YSXS+g(YRXS+YPXR+YSXP)=

(YR+gYP)XR+(YP+gYS)XP+(YS+gYR)XS

(9)

假設χ=YR+gYP,ξ=YP+gYS,μ=YS+gYR.XR,XP,XS表示收益概率,χ,ξ,μ表示收益值.

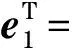
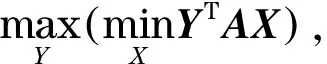
(10)

式中:i為確定性策略;ei為第i個位置為1,其他位置全為零的矩陣.

凸優化函數標準形式為

(11)

引入變量α表示內部最小化的值

(12)

矩陣向量表示為

(13)

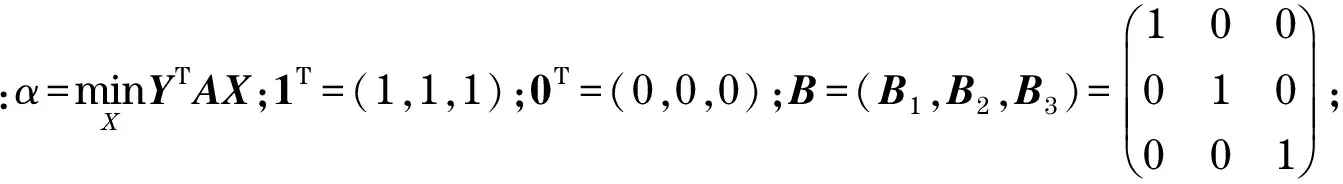
2.2鞍點方程

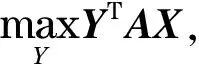
相當于

(14)

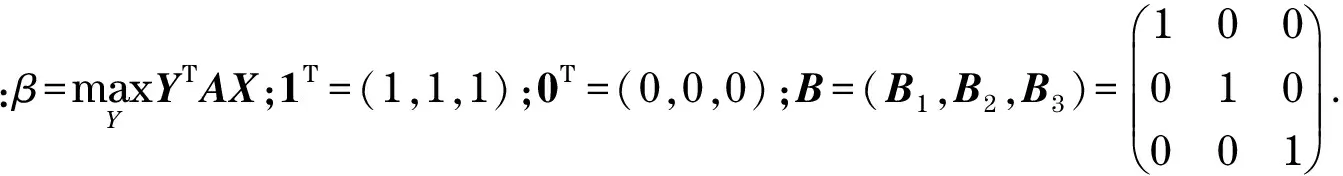
式(13)和式(14)分別為玩家X和Y的收益,兩式為對偶關系(在博弈系統中玩家Y和玩家X是對偶關系).

最初假設玩家X和Y有先后順序,實際上是玩家X和Y同時作決定.在此基礎上,結合式(13)和式(14),有

(15)

式(15)稱為鞍點方程,用于描述玩家獲得最大收益時的鞍點.式(13)和式(14)分別為式(15)的兩邊.

同理,玩家X的收益用鞍點方程表示為

(16)

用于描述系統收益最大值.其中式(16)的兩邊分別用式(17)和式(18)表示.

(17)

(18)

3 算 法

3.1Newton算法

本文提出的鞍點方程是用于表示系統收益最優的臨界方程,為驗證其正確性,利用Newton算法證明.

對于z∈domf,稱向量

Δznt=-2f(z)-1f(z)

(19)

為(f在z處的)Newton步徑[26].由2f(z)的正定性可知,除非f(z)=0,否則就有

(20)

因此Newton步徑為下降方向.

(21)

這是ν的二次凸函數,在ν=Δznt處達到最小值.因此,將z加上Newton步徑Δznt能夠極小化f在z處的二階近似[26].

凸優化問題

(22)

(23)

可將Newton方向Δznt及其相關向量w解釋為最優性條件

Cz*=D,f(z*)+CTz*=

ATy+CTν*=0

(24)

的線性近似方程組的解.用z+Δznt代替z*,用w代替ν*,并將第二個方程中的梯度項換成其在z附近的線性近似,從而得到

C(z+Δznt)=D,f(z+Δznt)+

CTw≈ATy+0+CTw=0

(25)

利用CX=D,以上方程變為

CΔznt=0,CTw≈-ATy

(26)

Newton方向Δznt由以下方程確定

(27)

式中,w是該二次問題的最優對偶向量.

Newton方向Δznt和Newton減量λ(z)分別為

(28)

3.2驗證理論

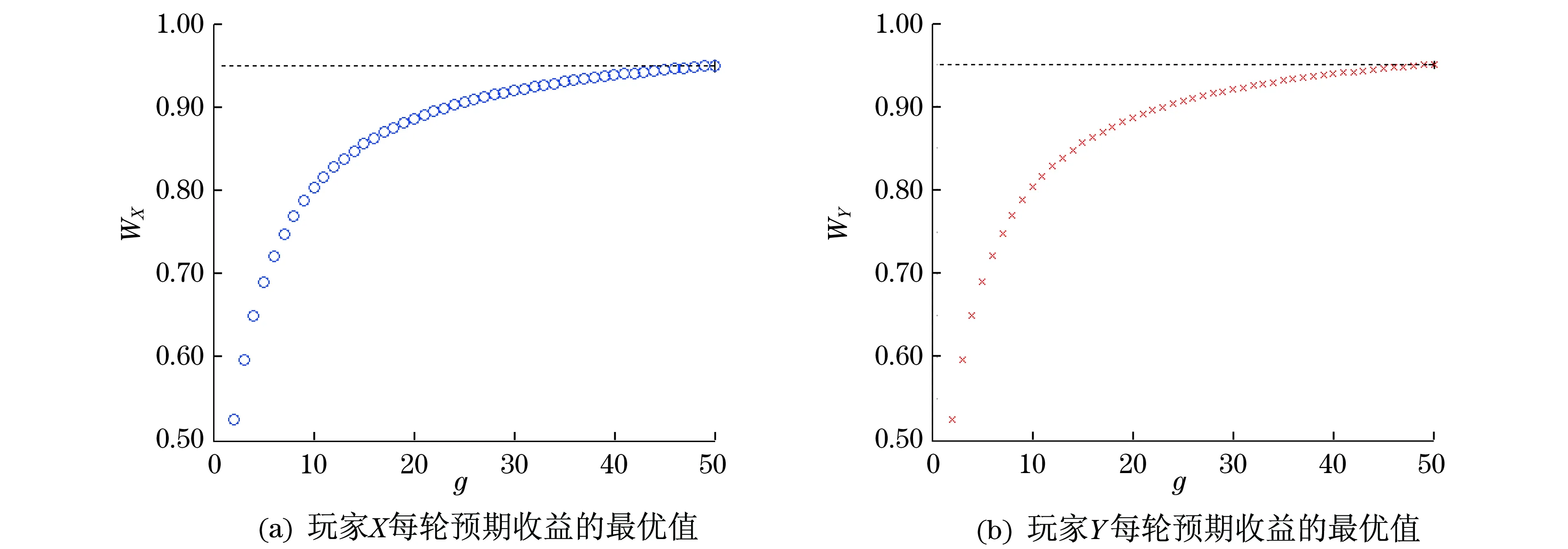
圖3 WX為玩家X獲得的最大回報值,WY為玩家Y獲得的最大回報值(單位為g1).Fig.3 Biggest gain of player X isWX,the biggest gain of player Y is WY (in units of g1).

4 結 論

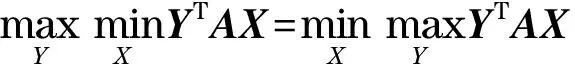
[1] WANG Z J,XU B,ZHOU H J.Social cycling and conditional responses in the rock-paper-scissors game[J].Scientific Reports,2014,4:5830.

[2] BIERNASKIE J M,GARDNER A,WEST S A.Multicoloured greenbeards,bacteriocin diversity and the rock-paper-scissors game[J].Journal of Evolutionary Biology,2013,26(10):2081-2094.

[3] LAIRD R A.Population interaction structure and the coexistence of bacterial strains playing ‘rock-paper-scissors’[J].Oikos,2014,123(4):472-480.

[4] LOERTSCHER S.Rock-scissors-paper and evolutionarily stable strategies[J].Economics Letters,2013,118(3):473-474.

[5] HE Q,MOBILIA M,T?UBER U C.Spatial rock-paper-scissors models with in homogeneous reaction rates[J].Physical Review E,2010,82(5):051909.

[6] SINERVO B,HEULIN B,SURGET-GROBA Y,et al.Models of density-dependent genic selection and a new rock-paper-scissors social system[J].The American Naturalist,2007,170(5):663-680.

[7] KERR B,RILEY M A,FELDMAN M W,et al.Local dispersal promotes biodiversity in a real-life game of rock-paper-scissors[J].Nature,2002,418(6894):171-174.

[8] BI Z D,ZHOU H J.Optimal cooperation-trap strategies for the iterated rock-paper-scissors game[J].PLoS One,2014,9(10):e111278.

[9] ZHOU H J.The rock-paper-scissors game[J].Contemporary Physics,2016,57(2):151-163.

[10] AUMANN R J,BRANDENBURGER A.Epistemic conditions for Nash equilibrium[J].Econometrica,1995,63(5):1161-1180.

[11] 汪筱陽,吳德偉,戴傳金.基于納什博弈論的功率控制策略及其牛頓迭代算法[J].電子設計工程,2013,21(1):74-76.

[12] BAHEL E,HALLER H.Cycles with undistinguished actions and extended rock-paper-scissors games[J].Economics Letters,2013,120(3):588-591.

[13] BAHEL E.Rock-paper-scissors and cycle-based games[J].Economics Letters,2012,115(3):401-403.

[14] WESSON E,RAND R.Hopf bifurcations in delayed rock-paper-scissors replicator dynamics[J].Dynamic Games and Applications,2016,6(1):139-156.

[15] SEMMANN D,KRAMBECK H J,MILINSKI M.Volunteering leads to rock-paper-scissors dynamics in a public goods game[J].Nature,2003,425(6956):390-393.

[16] LUBASHEVSKY I,KANEMOTO S.Scale-free memory model for multiagent reinforcement learning.Mean field approximation and rock-paper-scissors dynamics[J].The European Physical Journal B,2010,76(1):69-85.

[17] MOBILIA M.Oscillatory dynamics in rock-paper-scissors games with mutations[J].Journal of Theoretical Biology,2010,264(1):1-10.

[18] VERMA G,CHAN K,SWAMI A.Zealotry promotes coexistence in the rock-paper-scissors model of cyclic dominance[J].Physical Review E,2015,92(5):052807.

[19] SZOLNOKI A,PERC M.Zealots tame oscillations in the spatial rock-paper-scissors game[J].Physical Review E,2016,93(6):062307.

[20] 曾勇.基于博弈論的無線通信抗干擾關鍵技術研究[D].成都:電子科技大學,2014.

[21] JOSHI S,BOYD S.Sensor selection via convex optimization[J].IEEE Transactions on Signal Processing,2009,57(2):451-462.

[22] 唐璜,毛璐.基于博弈論的軟件動態調控策略的研究與實現[J].信息與電腦,2012(2):50-51.

[23] MATTINGLEY J,BOYD S.Cvxgen:a code generator for embedded convex optimization[J].Optimization and Engineering,2012,13(1):1-27.

[24] WANG T,JOBREDEAUX R,PANTEL M,et al.Credible autocoding of convex optimization algorithms[J].Optimization and Engineering,2016,17(4):781-812.

[25] 劉海姣,趙書田.一種關聯博弈的軟件調度線性規劃控制算法[J].微電子學與計算機,2016,33(7):121-124.

[26] BOYD S,VANDENBERGHE L.Convex optimization[J].IEEE Transactions on Automatic Control,2006,51(11):1859-1859.

OptimizingStrategyforGameTheorySystemBasedontheConvexOptimizationMethod

TIAN Wei,LIUYifang

(CollageofScience,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The convex optimization,which serves as a new optimized method,can be fully applied to the game theory system,aiming at maximizing the payoff of the game systems (for all players).The two-person non-zero-sum matrix was introduced to describe the equivalent of payoff in the hypothetical game theory system for making quantitative analyses and getting maximal payoff of the system.A saddle point equation was created to be the critical equation of the optimal value of the game theory system and Newton’s algorithm was used to simulate the game model.The simulation results show that,the results are consistent with the theoretical hypothesis values.The method was tested and verified to be feasible and accurate.The work is helpful for deeply understanding the game theory system and reasonably applying the convex optimization.

simulation;convexoptimization;gametheorysystem;saddlepoint

1007-6735(2017)05-0420-05

10.13255/j.cnki.jusst.2017.05.003

2017-05-21

國家自然科學基金資助項目(10874118)

田 偉(1977-),男,講師.研究方向:系統分析與集成.E-mail:tianwei@usst.edu.cn

O174.13

A

(編輯:丁紅藝)