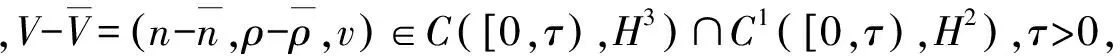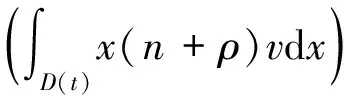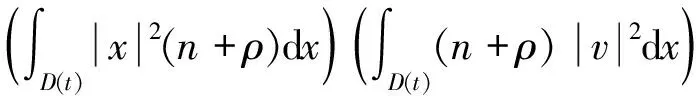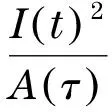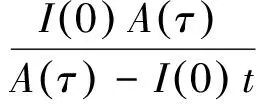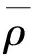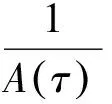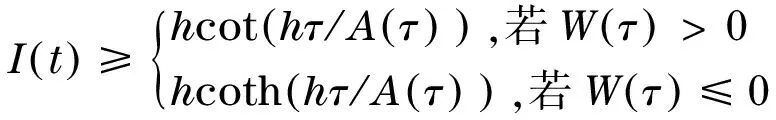一類三維非粘性可壓流體力學方程解的有限傳播速度及奇異性

,

(1.河海大學 理學院,南京 211100; 2.河海大學 文天學院,馬鞍山 243031)

一類三維非粘性可壓流體力學方程解的有限傳播速度及奇異性

韓平1,徐國靜2

(1.河海大學 理學院,南京211100;2.河海大學 文天學院,馬鞍山243031)

研究了一類三維非粘性的可壓流體力學方程局部光滑解的性質,證明了當方程的初值滿足一定條件時,解在有限時間內會形成奇異.討論了此方程具有有限傳播速度,并利用有限傳播速度討論解的奇異性.解的有限傳播速度對研究解的奇異性起非常重要的作用.

三維非粘性可壓流體力學方程; 有限傳播速度; 解的奇異性

1 問題的提出

研究了Vlasov-Fokker-Planck與Navier-Stokes方程的一類極限模型[1],在三維框架下,方程為

(1)

式中:n(x,t)∈+,ρ(x,t)∈+,均表示密度;v(x,t)∈3,表示流速;x∈3,表示空間變量;t>0,表示時間變量;壓力p與密度相關,滿足p=p(n,ρ)=n+ργ,γ>1.

在非粘性情況下,μ=0,在粘性情況下,μ>0.

若γ=1,μ=0,將n+ρ看成一個變量,則方程(1)變為經典的Euler方程.本文主要研究γ>1,μ=0的情況.

對方程(1),給定初值

(n,ρ,v)|t=0=(n0,ρ0,v0)

(2)

Sideris[2]研究了二維可壓流體方程的衰減奇異結構;Nishida[3]研究了一維帶阻尼項的Euler方程光滑解的整體存在性;Dafermos[4]研究了耗散項能阻止波動對解的破壞;Li[5]研究了帶線性退化的一般雙曲系統整體光滑解的存在性;Sideris等[6]研究了高維帶線性阻尼的Euler方程解的整體存在性及爆破.

利用一般雙曲方程的局部光滑解存在性理論,方程(1)的局部光滑解是存在的[7-8].雙曲型方程的特點是在一定條件下,解在有限時間內會爆破,本文主要討論方程(1)的有限傳播速度,并利用有限傳播速度討論解的爆破.

雙曲型方程光滑解的局部存在性定理是眾所周知的結論.對于一維的雙曲型方程的光滑解的有限時間爆破,特別是單個方程,如Burgers方程,可以利用特征線方法給出很好的描述,這一類方法對于研究高維方程組有一定的困難[5].本文借鑒文獻[6],通過定義一個積分平均量,得出式(1)滿足一定的微分不等式,從而證明了高維雙曲型方程組的解在一定條件下不能整體存在.由于光滑解的有限時間爆破,所以,需要進一步討論方程的弱解,即滿足積分方程的L∞解,此時方程中的導數應理解為解的弱導數[5].弱解的存在性以及光滑解的奇異形成機制,即解的導數在某范數下的爆破將是本文研究的內容.

2 局部存在性和有限傳播速度

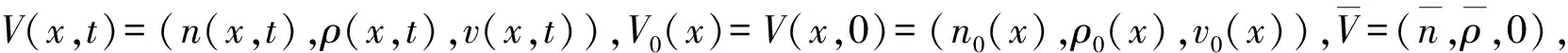
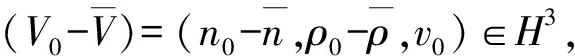
定理1可利用不動點定理證明,可參考文獻[7-8].現利用定理1證明方程(3)的解具有有限傳播速度.

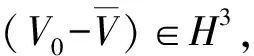
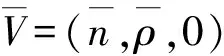
(3)

(4)

其中

(5)

任取τ∈[0,t),定義斜截錐:Gτ={(y,s):|y-x|≤σ(t-s),0≤s≤τ},將式(4)在Gτ上積分,利用散度定理,式(4)左邊項積分,可得

(6)

利用Cauchy不等式,可得

同理,

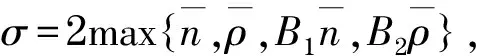
(7)

由此可知,式(6)的第3項積分是非負的,現估計式(4)的右邊項在Gτ上的積分.

利用Cauchy不等式,式(5)中E1,E2,E3分別估計為

同理,

式(4)的右邊項在Gτ上積分,可得

(8)

存在常數C>0,合并式(6)～(8),則式(4)化簡為

令

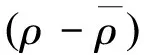
則有

由Gronwall不等式可得

因此,取x∈3,滿足|x|≥R+σt.若|y-x|≤σt,則有|y|≥R.因為?{x∈3||x|≤R},所以,V(y,0)=0.由上式可知,f(0)=0,f(τ)=0,即V(x,t)=0.定理2證畢.

3 解的奇異性

利用方程(1)得到一些等式和微分不等式,利用這些微分不等式可以獲得相應的估計,利用有限傳播速度定理2來證明當初值滿足一定條件時,方程(1)的局部光滑解在有限時間內的奇異性.有限傳播速度起關鍵作用.

固定R>0,定義:

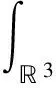
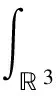
D(t)={|x|

|D(t)|是D(t)的體積.

(9)

其中,C0>0.‖·‖表示3上的L2的范數.

證明由式(1)的前2個方程可知

F1(t)=F1(0),F2(t)=F2(0)

則

F(t)=F(0)

(10)

利用式(1)的第3個方程及分部積分,可得

(11)

利用P(n,ρ)=n+ργ,γ>1的凸性,可得

(12)

由式(11)和式(12)可得

(13)

假設解被整體定義,利用式(10)和Cauchy-Schwarz不等式證明式(9).

所以,

(14)

現證明v(t)的L2模下界估計.因為,n∈+,ρ∈+,故式(1)中所以,有

(15)

將式(15)兩邊再積分,整理得

(16)

利用Cauchy-Schwarz不等式,由定理2,及|n+ρ|的一致有界性,有

(17)

其中,Ci>0,i=0,1,2,3.

由式(16)和式(17)可得

(18)

由式(14)和式(18)可得

定理3證畢.

I(0)>A(T)/T

(19)

或

I(0)>A(T)(T-1+J(T))

(20)

則τ

證明假設式(1)的解在[0,τ)上存在,利用有限傳播速度定理2和Cauchy-Schwarz不等式,可得

(21)

利用式(10),可得

(22)

聯立式(13),(21),(22),可得微分不等式

t∈[0,τ)

因為，A(t)是增的,所以,

t∈[0,τ)

(23)

因此,τ

令I(0)2+W(τ)>0,此時,I(t)是單調遞增的.令h2=|W(τ)|,則

將上式在0～τ上積分,得

則τ

定理5證畢.

[1] MELLET A,VASSEUR A.Asymptotic analysis for a Vlasov-Fokker-Planck/compressible Navier-Stokes system of equations[J].Communications in Mathematical Physics,2008,281(3):573-596.

[2] SIDERIS T C.Delayed singularity formation in 2D compressible flow[J].American Journal of Mathematics,1997,119(2):371-422.

[3] NISHIDA T.Nonlinear hyperbolic equations and related topics in fluid dynamics[M].Paris:Université de Paris-Sud,1978.

[4] DAFERMOS C M.Can dissipation prevent the breaking of waves[C]∥Transactions of the Twenty-Sixth Conference of Army Mathematicians.Research Triangle Park.Research Triangle Park,1981:187-198.

[5] LI T S.Global classical solutions for quasilinear hyperbolic systems[M].Chichester:John Wiley & Sons,1994.

[6] SIDERIS T C,THOMASES B,WANG D H.Long time behavior of solutions to the 3D compressible Euler equations with damping[J].Communications in Partial Differential Equations,2003,28(3):795-816.

[7] MAJDA A.Compressible fluid flow and systems of conservation laws in several space variables[M].New York:Springer,2012.

[8] KATO T.The Cauchy problem for quasi-linear symmetric hyperbolic systems[J].Archive for Rational Mechanics and Analysis,1975,58(3):181-205.

FinitePropagationSpeedandSingularityoftheSolutionforaSystemofThree-DimensionalInviscidCompressibleFluidEquations

HAN Ping1,XUGuojing2

(1.CollegeofScience,HohaiUniversity,Nanjing211100,China; 2.WentianCollege,HohaiUniversity,Maanshan243031,China)

The properties of local smooth solutions of a system of three-dimensional inviscid compressible fluid equations were investigated.It is proved that a singular solution will be generated in the limited time when the initial value of the equations satisfies some conditions.The finite speed of propagation was discussed and used to study the singularity of the solution.The finite speed of propagation of the solution plays a very important role to study the singularity of the solution.

three-dimensionalinviscidcompressibleequation;finitepropagationspeed;singularsolution

1007-6735(2017)05-0425-05

10.13255/j.cnki.jusst.2017.05.004

2017-04-27

國家自然科學基金資助項目(11201116)

韓 平(1991-),女,碩士研究生.研究方向:偏微分方程.E-mail:632401352@qq.com

O175.2

A

(編輯:石 瑛)