基于申威眾核處理器的混合并行遺傳算法

趙瑞祥，鄭 凱，劉 垚，王 肅，劉 艷，沈煥學，周謙豪

(1.華東師范大學 計算機科學與軟件工程學院，上海 200062； 2.數學工程與先進計算國家重點實驗室，江蘇 無錫 214215；3.華東師范大學 經濟與管理學部，上海 200062)(*通信作者電子郵箱kzheng@cs.ecnu.edu.cn)

基于申威眾核處理器的混合并行遺傳算法

趙瑞祥1,2，鄭 凱1,2*，劉 垚1,2，王 肅1,2，劉 艷1,2，沈煥學1,2，周謙豪3

(1.華東師范大學 計算機科學與軟件工程學院，上海 200062； 2.數學工程與先進計算國家重點實驗室，江蘇 無錫 214215；3.華東師范大學 經濟與管理學部，上海 200062)(*通信作者電子郵箱kzheng@cs.ecnu.edu.cn)

傳統遺傳算法求解計算密集型任務時，適應度函數的執行時間增加相當快，致使當種群規模或者進化代數增大時，算法的收斂速度非常緩慢。基于此，設計了“粗粒度-主從式”混合式并行遺傳算法(HBPGA)，并在目前TOP500上排名第一的超級計算機神威“太湖之光”平臺上實現。該算法模型采用兩級并行架構，結合了MPI和Athread兩種編程模型，與傳統在單核或者一級并行構架的多核集群上實現的遺傳算法相比，在申威眾核處理器上實現了二級并行，并得到了更好的性能和更高的加速比。實驗中，當從核數為16×64時，最大加速比達到544，從核加速比超過31。

混合并行遺傳算法；神威“太湖之光”；眾核；MPI；Athread

0 引言

隨著科技進步，計算密集型任務需求與日俱增，但許多情況下單純的串行計算已不能滿足當前的要求，單個芯片的性能提高遇到了瓶頸[1]：越來越高的集成度，導致高功耗[2]和散熱問題難以解決。采用多核或眾核已成為提高處理能力的重要手段，相應的程序也需要從串行轉向并行。但由于串行程序與并行程序存在巨大的差異，無法自動轉換，許多用串行方式實現的應用移植到眾核平臺運行面臨不小的挑戰。

目前關于并行遺傳算法的研究多數在多核平臺實現[3-5]，并采用消息傳遞接口(Message-Passing-Interface, MPI)編程模型，性能和加速比的提升受到主核數量的限制，當適應度函數的計算量復雜時性能和加速比的提升不明顯。也有關于在通用并行計算架構[6-9](Compute Unified Device Architecture, CUDA)上基于圖形處理器(Graphics Processing Unit, GPU)的粗粒度并行遺傳算法的實現報道[10]。為了與GPU架構兼容，在CUDA軟件模型中使用簡化的單向環移動，提高了遷移速度[11]。但受GPU結構的限制，只適用單指令多數據流(Single Instruction Multiple Data, SIMD)類型的數據并行，內部各處理核之間不允許通信，使其應用范圍受到很大局限。曾有學者試圖利用現場可編程門陣列(Field-Programmable Gate Array, FPGA)來實現遺傳算法的并行化，但很難實現。文獻[12-13]指出，FPGA在硬件架構和優化時，靈活性較弱，算法中的許多部分不能很好地映射到硬件。而本文的實驗平臺采用國產超算“神威·太湖之光”。該機是世界上首臺峰值運算性能超過十億億次量級的超級計算機，目前在TOP500中排行第一，也是中國首臺全部采用國產處理器構建的超級計算機。該機采用我國自主研制的“申威 26010”眾核處理器，通過主核和從核間的并行協作，可以達到極高的并行計算能力。該處理器與GPU相比具有較強的通信和同步能力，與FPGA相比具有較好的靈活性，突出的特點是從核處理能力較強。文獻[14]論證發現，“申威 26010”上逾98%的理論性能均源自于從核。所以編程時將串行的、復雜的、需要內存容量大的工作放在擁有較多內存的主核上完成，而獨立的、可以并行執行的、計算密集型的工作放在從核完成，更能體現出該眾核架構的優勢。

由于遺傳算法的種群中每個個體之間的數據獨立性強，具有天然的并行性，非常適合于在大規模并行機上實現。基于該平臺，本文將典型的遺傳算法進行了二級并行化設計，并結合兩種編程模型，MPI和Athread(SW26010專用加速線程庫)將其實現。目前已有的并行遺傳算法一般是實現一級并行(MPI模式)，尚未看到有相關的研究基于申威“26010”眾核處理器實現遺傳算法的二級并行。本文的工作在這個領域是一種新的嘗試。

1 混合式的二級并行模型的設計與實現

1.1 并行遺傳算法模型介紹

目前遺傳算法的并行模型可分為四種：主從式模型、粗粒度模型、細粒度模型和混合模型[15]。

曾國蓀等[16]指出，主從式模型的優點是簡單，且速度和效率優于串行遺傳算法，但缺陷是經常會出現主從節點機負載不均衡、通信瓶頸和延遲問題。在主從式模型中，選擇、交叉和變異操作由主節點機串行執行，而適應度評價由從節點機并行執行，所以這種模型適合適應度函數復雜的遺傳算法，對于適應度函數較簡單的情況，它將失去并行執行的優勢。

粗粒度模型中每經過一定的進化代，各個子群體間將交換若干個個體，一方面用來引入更優良的個體，另一方面豐富種群的多樣性，防止未成熟早收斂現象。對于粗粒度模型，確定遷移規模相當重要，遷移規模由遷移率、遷移周期兩個參數控制，通常遷移率越大則遷移周期越長[17]。鄭志軍等[18]通過實驗證明，大規模的遷移或遷移周期太短將導致通信開銷增多；而遷移規模太小又容易形成局部最優解，影響解的質量；遷移周期太長則會導致優秀個體不能及時傳播，反而降低收斂速度。

細粒度模型具有維持種群多樣性從而抑制早熟現象及能實現高度并行化等優勢[19]。但由于每個個體需要單獨占用一個節點，導致該模型通信開銷大，并行機難以承受，并且研究人員難以找到適用于該模型的并行機。

混合模型[20-21]是將上述三種模型混合形成的層次模型，一般有三種：粗粒度-細粒度、粗粒度-粗粒度、粗粒度-主從式。結合粗粒度模型適合遷移操作的特點和主從式模型適合計算密集型任務的優勢，本文采用粗粒度-主從式模型，上層用粗粒度模型，下層用主從式模型。

1.2 混合式的二級并行模型的設計

以往并行遺傳算法，實現的一般是一級并行(MPI模式)，存在通信延遲、負載不均衡、核的數量少、同步困難等問題，加速比較低，不能充分發揮出并行算法的優勢。考慮到“申威 26010”眾核處理器的物理結構和“粗粒度-主從式”混合并行遺傳算法邏輯結構相似，本文設計和實現了混合式的二級并行的遺傳算法，可以充分利用申威眾核架構實現遺傳算法的高度并行。

如圖1[14]所示，一個處理器節點擁有4個核組(Core Group, CG)，每一個核組由一個主核(Management Processing Element, MPE)和64個按照8×8的Mesh拓撲結構構成的從核(Computing Processing Element, CPE)組成，且核組間由片上內部網絡互聯，并支持低延遲的寄存器級數據通信。圖2中p1、p2、p3、p4分別代表4個子種群，每一個子種群就是一個島，各島之間按粗粒度模型并行進化，每一子種群又按分配的從核數量分成n組，除最后一組外，其他各組包含同等數量的個體，組數n不超過N(N為每個核組內的從核數，當前為64)。組內的個體按主從式模型并行進化，初始化、選擇、交叉、變異在主核中運行，適應度計算在從核中進行。通過將遺傳算法中的各子種群映射到核組的主核上，將子種群內的各組映射到該核組的從核上，核組間采用粗粒度模式并行，核組內采用主從式模式并行，實現了種群間和種群內的兩級并行，提高了算法的收斂速度和求解質量。

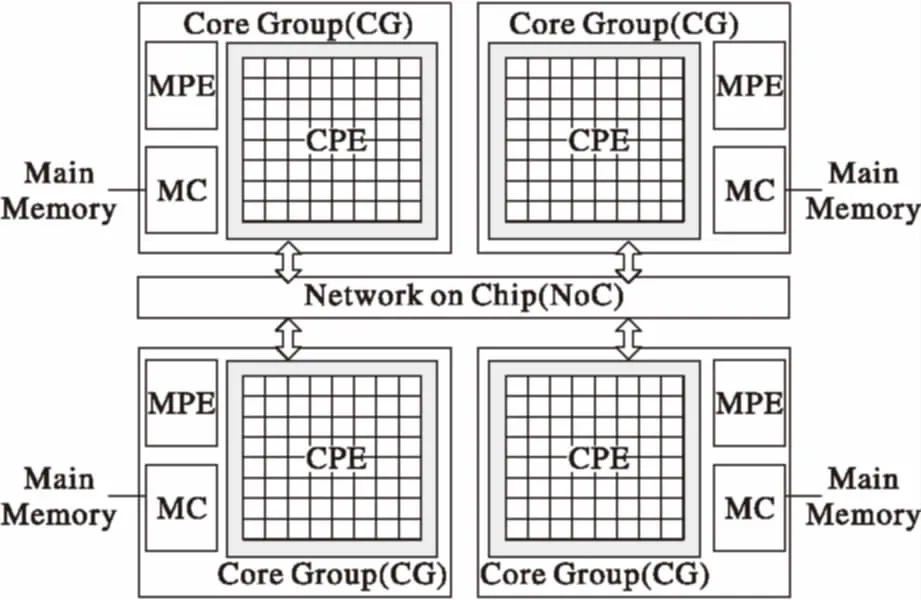
圖1 “申威 26010”眾核處理器架構

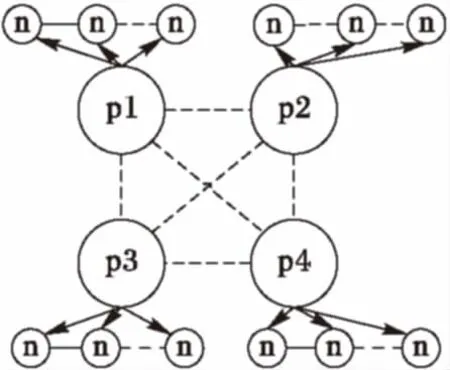
圖2 混合并行遺傳算法結構

如圖3所示，為本文采用的主從加速并行的并行模型。主從加速并行方法是“太湖之光”計算機系統支持的兩級并行方法，從核根據實際應用課題的核心計算內容進行眾核加速，而主核完成同步、通信、I/O和串行代碼的計算。本文的核心計算內容為適應度函數計算。為完成適應度函數的眾核計算，首先初始線程庫和創建線程組，啟動核組中的所有可用資源。然后將種群內個體信息通過Athread加載到對應從核上，此時主核處于等待狀態，從核進行眾核加速計算，計算完成后通過Athread將個體信息寫回主核。最后主核在確認線程組所有從核都完成任務后，停止從核流水線，關閉從核組，完成本次眾核加速計算任務。

圖3 主從加速并行示意圖

1.3 混合式的二級并行模型的實現

就并行編程來說，本文結合了消息傳遞和共享內存兩種編程模型，即MPI和Athread的混合編程。MPI一般用于主核間的通信。而節點內部的工作可通過“申威 26010”加速線程庫(Athread庫)完成，它是針對主從加速編程模型所設計的程序加速庫，其目的是為了用戶能夠方便、快捷地對核組內的線程進行控制和調度，從而更好地發揮核組內多運算核心的加速性能[22-23]。該混合編程模型分為兩層：上層為粗粒度模型中島間的并行，即每一個島對應一個進程；下層為島內部的并行，采用主/從式模型，主核上的進程啟動多個從核上的線程并行執行，每一個從核運行一個線程，從而實現了進程和線程的兩級并行。

進程并行的實現：將遺傳算法的求解任務分解為若干個相對獨立的子任務，為每一個子任務分配一個主核，即一個進程。子任務間的通信，使用MPI模型實現。進程間可以同步執行，也可以異步執行。文獻[24]表明，異步執行由于達到執行條件時不需要獲取其他進程狀態就可以執行，減少了等待時間，所以比同步速度更快。

線程并行的實現：將上一步分解完成的子任務繼續分解為二級子任務，每一個二級子任務對應核組的一個從核，即一個線程。因為核組內的若干線程共享內存，所以節點內使用共享存儲的Athread實現并行編程。

本文采用混合并行編程模型的目的是充分利用申威眾核系統的硬件資源，保證負載均衡，降低通信代價，從而提高并行程序的性能。若采用單一的MPI并行編程，實際只利用了主核的性能，核組內的從核沒有能夠發揮作用，浪費了寶貴的計算資源。采用混合并行編程模型后，由于進程內包含若干線程，各線程通過利用從核資源，使進程執行時間縮短，進程間通信延遲也相應降低，高效實現了進程和線程的兩級并行，算法的性能得到較大的提升。

2 混合并行遺傳算法描述及實現

2.1 混合并行遺傳算法描述及流程

混合并行遺傳算法流程如圖4所示。

圖4 混合并行遺傳算法流程

主要步驟如下。

1)初始化操作。程序通過調用MPI_Comm_size()函數獲得總進程數，并設定第0號進程為主進程，其他進程為從進程。主進程調用MPI_Bcast()將染色體上下限參數以廣播的方式發送給其他進程。從進程收到參數后，獨立并行地在相應主核內初始化種群。

2)適應度計算操作。從進程在主核內串行執行交叉、變異等操作，而后通過對應線程完成適應度計算。首先從核調用Athread_get()函數，從主核內獲取種群內個體信息，然后在從核內并行執行個體適應度計算，最后從核調用Athread_put()函數，將計算好的個體信息返回主核。

3)遷移操作。當遺傳算法中每代的個體適應度值計算完成后，通過輪盤賭策略選出將要遷移的若干個體(本文為3個)，進程通過調用MPI_Isend()函數，將選中的若干個體遷移到其他進程，而后通過MPI_Recv()函數接收來自其他進程的遷移個體，并隨機替換本種群中適應值小的若干個體。

4)歸約操作。若當前進化代數達到最大進化數，則跳出循環，停止執行以上操作，進入最后的歸約操作。進程調用MPI_Reduce()函數，在各子種群中選出最優個體作為最后結果。

混合并行遺傳算法模型可以從兩個方面實現，一是并行編程模型實現，二是混合并行遺傳算法實現。

2.2 混合并行遺傳算法實現

本文采用“粗粒度-主從式”混合并行遺傳算法模型。模型包括上下兩層，上層由粗粒度并行遺傳算法模型構成，該層將整個種群劃分為若干子種群，每一個子種群稱作一個島，對應一個核組的主核。島與島之間獨立并行的執行遺傳操作，當經過固定的進化代數，種群之間通過某種遷移策略進行島之間的個體遷移，以交換種群信息，使種群內優良個體得以保留，種群多樣性得以保持。下層由主從式并行遺傳算法模型構成，島內的遺傳操作包括遷移、變異、交叉、適應度計算等，除了適應度計算，其他操作都由在主核上運行的進程串行執行，而進程內啟動的若干線程按主從式模型在從核上進行適應度計算。

3 算法測試與結果分析

本文的測試函數為標準測試函數[25-26]:

通過求函數的最小值測試遺傳算法的性能。由于測試函數計算量小，執行時間短，不能充分體現出超算中從核的高性能。文獻[27]指出，可以在適應度函數的計算語句中加入一個掛起語句，可以根據問題的規模，設置將系統掛起的時間，模擬等時間的計算量，以分析遺傳算法針對不同規模問題的求解性能。本文也采用在適應度函數內加入掛起語句來增加計算量以模擬大規模問題的求解。

本實驗的運算平臺為無錫超算中心的神威“太湖之光”超級計算機，其硬件配置如表1[28]所示。遺傳算法具體參數如下：雜交概率為0.8，變異概率為0.15，遷移個體為3。

為驗證所設計HBPGA算法的性能，同時也為了測試申威眾核處理器中從核的性能，實驗采用4個評價指標：執行時間、從核加速比、加速比和求解精度。Rastrigin函數的測試結果反映在圖5、圖6和表3中，Hansen函數和Rosenbrock函數的測試結果反映在圖7和圖8中。

表1 神威“太湖之光”主要參數

圖5的種群大小為198，使用主核數為6，每個主核配11個從核，橫坐標是進化代數，縱坐標是執行時間。圖中MPI代表僅使用MPI通信，hybrid表示同時使用了MPI和Athread，即本文的HBPGA算法。由圖5所示，HBPGA的執行時間和執行時間的增長速度遠小于純MPI，執行速率最多提高了12.7倍。

圖5 兩類算法基于Rastrigin函數的執行時間

一般并行算法性能的提升使用加速比指標，但本文的算法使用了大量從核處理器，需要有新的衡量指標即從核加速比來衡量從核的性能。從核加速比定義如下：固定的并行問題w，獲取僅使用主核運行的情況下的并行運行時間Tg以及獲取主核和從核共同進行處理情況下的運行時間為Tc，得到從核加速比S=Tg/Tc。獲取串行執行時間Ts，得到加速比H=Ts/Tc。

表2的種群大小107 520，最大執行代數20，每個主核配64個從核。已測得串行執行時間為13 683.185 6 s。通過變化主核數得到表3。由表3可知，HBPGA隨著主核的增加，從核加速比不斷增加，當主核數為16時(從核數為16×64)，加速比達到544.38，從核加速比為31.85。

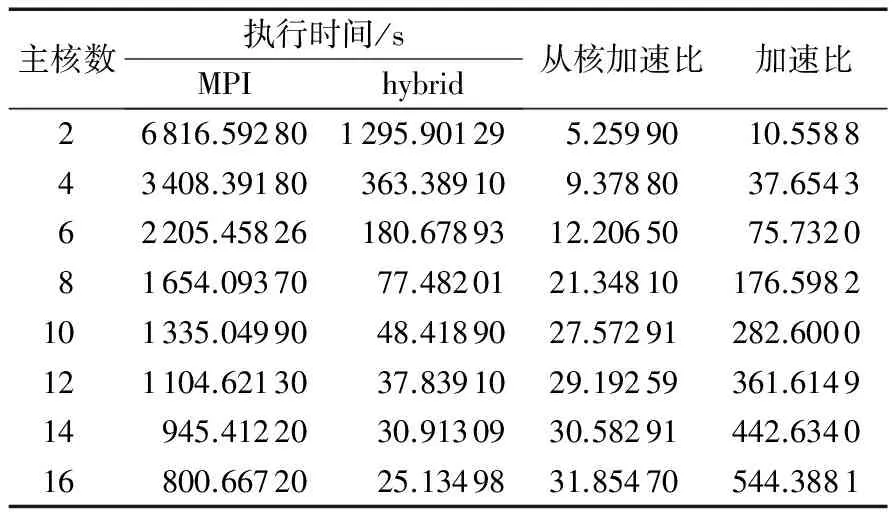
表2 從核加速比與主核數的關系(固定從核數)

為考察主核固定情況下從核增加對性能的影響，將主核數固定為10，逐步增加從核數，得到圖6。圖6中種群大小6 000，最大執行代數20。圖中顯示，隨著從核數的增加，HBPGA的從核加速比隨之增加。當從核數達到60時，從核加速比達到最大值24.74。

為衡量本文提出的HBPGA算法對解的質量的影響，采用Rastrigin函數進行了測試。測試中，種群大小設為198，執行30次實驗，都能收斂，平均收斂代數為11.9，優于串行算法的收斂代數(同等參數約為15)。實驗還使用Hansen函數和Rosenbrock函數在同等進化代數下對算法的執行時間進行了測試(圖7和圖8)，結果表明，與一級并行的MPI模型的算法相比，HBPGA算法在申威眾核處理器下明顯具有更短的執行時間。

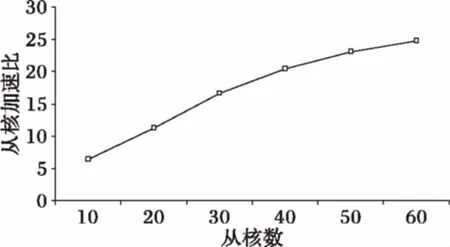
圖6 從核加速比與從核的關系(固定主核數)

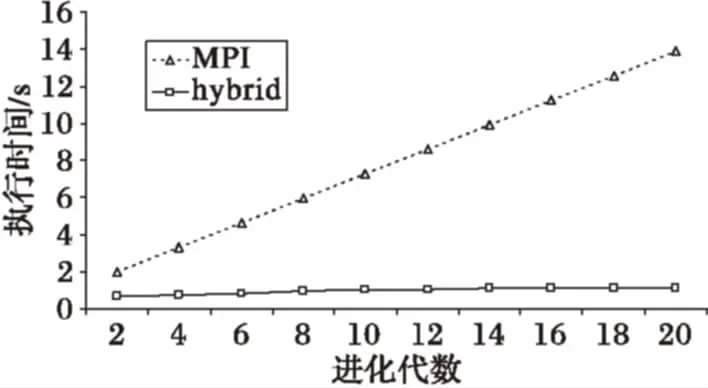
圖7 兩類算法基于Hansen函數的執行時間

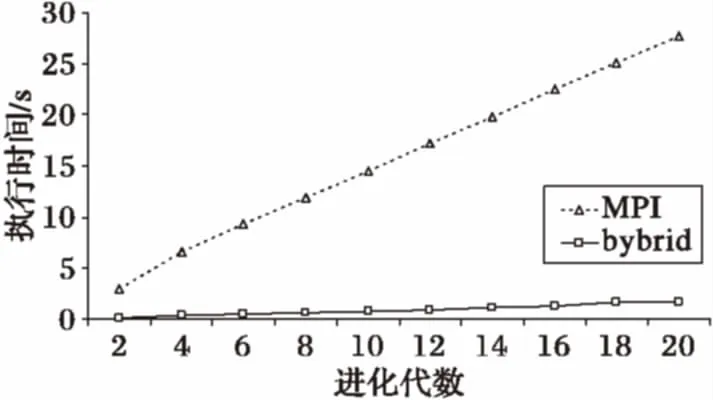
圖8 兩類算法基于Rosenbrock函數的執行時間

4 結語

本文通過分析申威眾核的物理拓撲和并行遺傳算法邏輯結構，并結合兩者的特點，設計出基于申威眾核的“粗粒度-主從式”混合并行遺傳算法，并進行了性能的比較和分析。該算法模型在眾核架構上具有一定的通用性，可以通過替換不同的適應度函數解決不同的問題，應用于不同場景。利用MPI和Athread兩種并行編程工具，使所設計的算法在申威眾核處理器上實現進程級和線程級的兩級并行。最后，對混合并行遺傳算法進行了實驗，實驗表明，不論與傳統串行遺傳算法還是單純采用MPI的并行遺傳算法比較，本文提出的基于申威眾核處理器的混合并行遺傳算法在求解速度和收斂代數方面都有明顯提高。

本文針對申威眾核處理器和并行遺傳算法進行了研究，還有很多后續的工作有待開展，如，對申威眾核架構更深層次的研究和分析，對本文提出的混合并行遺傳算法進一步性能優化，以及將算法應用于車輛導航、物流配送等組合優化問題等。

References)

[1] ESMAEILZADEH H, BLEM E, AMANT R S, et al. Dark silicon and the end of multicore scaling [C]// Proceeding of the 38th Annual International Symposium on Computer Architecture. New York: ACM, 2011: 365-376.

[2] 鄭方,張昆,鄔貴明,等.面向高性能計算的眾核處理器結構級高能效技術[J].計算機學報,2014,37(10):2176-2186.(ZHENG F, ZHANG K, WU G M, et al. Architecture techniques of many-core processor for energy-efficient in high performance computing [J]. Chinese Journal of Computers, 2014, 37(10): 2176-2186.)

[3] ZHENG L, LU Y, GUO M, et al. Architecture-based design and optimization of genetic algorithms on multi- and many-core systems [J]. Future Generation Computer Systems, 2014, 38(3): 75-91.

[4] UMBARKAR A J, JOSHI M S, HONG W C. Multithreaded Parallel Dual Population Genetic Algorithm (MPDPGA) for unconstrained function optimizations on multi-core system [J]. Applied Mathematics and Computation, 2014, 243: 936-949.

[5] 丁孟為.遺傳算法在多核系統上的性能分析和優化[D].上海：上海交通大學,2012.(DING M W. Performance analysis and optimization of genetic algorithms on multi-core systems [D]. Shanghai: Shanghai Jiao Tong University, 2012.)

[6] NVIDIA Corporation. NVIDIA’s next generation CUDA compute architecture: FERMI [EB/OL]. [2016- 09- 15]. http://www.nvidia.com/content/PDF/fermi_white_papers/NVIDIA_Fermi_Compute_Architecture_Whitepaper.pdf.

[7] LIU X, SMELYANSKIY M, CHOW E, et al. Efficient sparse matrix-vector multiplication on x86-based many-core processors [C]// Proceedings of the 27th International ACM Conference on International Conference on Supercomputing. New York: ACM, 2013: 273-282.

[8] SAINI S, JIN H, JESPERSEN D, et al. An early performance evaluation of many integrated core architecture based SGI rackable computing system [C]// Proceedings of the International Conference on High Performance Computing, Networking, Storage and Analysis. New York: ACM, 2013: Article No. 94.

[9] 巨濤,朱正東,董小社.異構眾核系統及其編程模型與性能優化技術研究綜述[J].電子學報,2015,43(1):111-119.(JU T , ZHU Z D, DONG X S. The feature, programming model and performance optimization strategy of heterogeneous many-core system: a review [J]. Acta Electronica Sinica, 2015, 43(1): 111-119.)

[10] POSPICHAL P, JAROS J, SCHWARZ J. Parallel genetic algorithm on the CUDA architecture [C]// Proceedings of the 2010 European Conference on the Applications of Evolutionary Computation, LNCS 6024. Berlin: Springer, 2010: 442-451.

[11] XUE Y, QIAN Z, WEI G, et al. An efficient Network-on-Chip (NoC) based multicore platform for hierarchical parallel genetic algorithms [C]// Proceedings of the 8th IEEE/ACM International Symposium on Networks-On-Chip. Piscataway, NJ: IEEE, 2014:17-24.

[12] GUO L, THOMAS D B, GUO C, et al. Automated framework for FPGA-based parallel genetic algorithms [C]// Proceedings of the 2014 24th International Conference on Field Programmable Logic and Applications. Piscataway, NJ: IEEE, 2014: 1-7.

[13] GUO L, GUO C, THOMAS D B, et al. Pipelined genetic propagation [C]// Proceedings of the 2015 IEEE 23rd Annual International Symposium on Field-Programmable Custom Computing Machines. Washington, DC: IEEE Computer Society, 2015: 103-110.

[14] 王一超,林新華,蔡林金,等.太湖之光上基于神威OpenACC 的GTC-P 移植與優化研究[EB/OL]. [2017- 05- 01]. http://max.book118.com/html/2017/0623/117447540.shtm.(WANG Y C, LIN X H, CAI L J, et al. Porting and optimizing GTC-P on TaihuLight supercomputer with Sunway OpenACC [EB/OL]. [2017- 05- 01]. http://max.book118.com/html/2017/0623/117447540.shtm.)

[15] 郭彤城,慕春棣.并行遺傳算法的新進展[J].系統工程理論與實踐,2002,22(2):15-23.(GUO T C, MU C D. The parallel drifts of genetic algorithms [J]. Systems Engineering—Theory & Practice, 2002, 22(2): 15-23.)

[16] 曾國蓀,丁春玲.并行遺傳算法分析[J].計算機工程,2001,27(9):53-55.(ZENG G S, DING C L. An analysis on parallel genetic algorithm [J]. Computer Engineering, 2001, 27(9): 53-55.)

[17] 李想,魏加華,傅旭東.粗粒度并行遺傳算法在水庫調度問題中的應用[J].水力發電學報,2012,31(4):28-33.(LI X, WEI J H, FU X D. Application of coarse-grained genetic algorithm to reservoir operation [J]. Journal of Hydroelectric Engineering, 2012, 31(4): 28-33.)

[18] 鄭志軍,鄭守淇.粗粒度并行遺傳算法性能分析[J].小型微型計算機系統,2006,27(6):1002-1006.(ZHENG Z J, ZHENG S Q. Performance analysis of coarse-grained parallel genetic algorithms [J]. Journal of Chinese Computer Systems, 2006, 27(6): 1002-1006.)

[19] BACH F R, JORDAN M I. Learning spectral clustering [J]. Advances in Neural Information Processing Systems, 2004, 16(2): 2006.

[20] XUE S, GUO S, BAI D. The analysis and research of parallel genetic algorithm [C]// Proceedings of the 2008 4th International Conference on Wireless Communications, Networking and Mobile Computing. Piscataway, NJ: IEEE, 2008: 1-4.

[21] CHENG C H, FU A W, ZHANG Y. Entropy-based subspace clustering for mining numerical data [C]// Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. New York: ACM, 1999: 84-93.

[22] 國家超級計算無錫中心.“神威·太湖之光”系統快速使用指南[EB/OL]. [2016- 09- 15]. http://www.nsccwx.cn/ceshi.php?id=13.(National Supercomputing Center in Wuxi. Guide of “Sunway TaihuLight” [EB/OL]. [2016- 09- 15]. http://www.nsccwx.cn/ceshi.php?id=13.)

[23] 國家超級計算無錫中心.“神威·太湖之光”編譯系統用戶手冊 [EB/OL]. [2016- 09- 15].http://www.nsccwx.cn/ceshi.php?id=12.(National Supercomputing Center in Wuxi. User’s manual of “Sunway Taihu-Light” computer compilation system [EB/OL]. [2016- 09- 15]. http://www.nsccwx.cn/ceshi.php?id=12.)

[24] ZHENG L, LU Y, GUO M, et al. Architecture-based design and optimization of genetic algorithms on multi-and many-core systems [J]. Future Generation Computer Systems, 2014, 38(3): 75-91.

[25] 胡玉蘭,潘福成,梁英,等.基于種群規模可變的粗粒度并行遺傳算法[J].小型微型計算機系統,2003,24(3):534-536.(HU Y L, PAN F C, LIANG Y, et al. Parallel genetic algorithm based on population size mutable coarse-grained [J]. Journal of Chinese Computer Systems, 2003, 24(3): 534-536.)

[26] TSOULOS I G, TZALLAS A, TSALIKAKIS D. PDoublePop: an implementation of parallel genetic algorithm for function optimization [J]. Computer Physics Communications, 2016, 209: 183-189.

[27] 凌實,劉曉平.基于MPI的主從式并行遺傳算法研究與實現[EB/OL].[2016- 12- 11]. http://xueshu.baidu.com/s?wd=paperuri%3A%2890fc2666352b25fdeaecbd242355ca7c%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.doc88.com%2Fp-0406863398613.html&ie=utf-8&sc_us=5462928728543012625.(LIN S, LIU X P. The study and implementation of master-slave parallel genetic algorithm based on MPI [EB/OL]. [2016- 12- 11]. http://xueshu.baidu.com/s?wd=paperuri%3A%2890fc2666352b25fdeaecbd242355ca7c%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Fwww.doc88.com%2Fp-0406863398613.html&ie=utf-8&sc_us=5462928728543012625.)

[28] FU H H, LIAO J F, YANG J Z, et al. The Sunway TaihuLight supercomputer: system and applications [J]. Science China Information Sciences, 2016, 59(7): 072001.

HybridparallelgeneticalgorithmbasedonSunwaymany-coreprocessors

ZHAO Ruixiang1,2, ZHENG Kai1,2*, LIU Yao1,2, WANG Su1,2, LIU Yan1,2, SHENG Huanxue1,2, ZHOU Qianhao3

(1.CollegeofComputerScienceandSoftwareEngineering,EastChinaNormalUniversity,Shanghai200062,China;2.StateKeyLaboratoryofMathematicalEngineeringandAdvancedComputing,WuxiJiangsu214215,China;3.FacultyofEconomicsandManagement,EastChinaNormalUniversity,Shanghai200062,China)

When the traditional genetic algorithm is used to solve the computation-intensive task, the execution time of the fitness function increases rapidly, and the convergence rate of the algorithm is very low when the population size or generation increases. A “coarse-grained combined with master-slave” HyBrid Parallel Genetic Algorithm (HBPGA) was designed and implemented on Sunway “TaihuLight” supercomputer which is ranked first in the latest TOP500 list. Two-level parallel architecture was used and two different programming models, MPI and Athread were combined. Compared with the traditional genetic algorithm implemented on single-core or multi-core cluster with single-level parallel architecture, the algorithm using two-level parallel architecture was implemented on the Sunway many-core processors, better performance and higher speedup ratio were achieved. In the experiment, when using 16×64 CPEs (Computing Processing Elements), the maximum speedup can reach 544, and the CPE speedup ratio is more than 31.

hybrid parallel genetic algorithm; Sunway “TaihuLight”; many-core; MPI; Athread

2017- 04- 10;

2017- 07- 11。

數學工程與先進計算國家重點實驗室開放基金資助項目(2016A05)。

趙瑞祥(1990—),男,吉林扶余人,碩士研究生,主要研究方向：計算機網絡、云計算; 鄭凱(1968—),男,浙江寧波人,副教授,博士,主要研究方向：計算機網絡、云計算; 劉垚(1981—),男,安徽靈璧人,高級工程師,碩士,主要研究方向：計算機網絡、高性能計算; 王肅(1980—),女,河南許昌人,講師,博士,主要研究方向：智能優化、信息系統; 劉艷(1976—),女,吉林通化人,助理研究員,博士,主要研究方向：智能優化、信息系統; 沈煥學(1992—),男,安徽安慶人,碩士研究生,主要研究方向：計算機網絡; 周謙豪(1997—),男,上海人,主要研究方向：高性能計算。

1001- 9081(2017)09- 2518- 06

10.11772/j.issn.1001- 9081.2017.09.2518

TP311.52; TP338.6

A

This work is partially supported by the Open Fund Project of the State Key Laboratory of Mathematical Engineering and Advanced Computing (2016A05).

ZHAORuixiang, born in 1990, M. S. candidate. His research interests include computer network, cloud computing.

ZHENGKai, born in 1968, Ph. D., associate professor. His research interests include computer network, cloud computing.

LIUYao, born in 1981, M. S., senior engineer. His research interests include computer network, high performance computing.

WANGShu, born in 1980, Ph. D., lecturer. Her research interests include intelligent optimization, information system.

LIUYan, borin in 1976, Ph. D., assistant research fellow. Her research interests include intelligent optimization, information system.

SHENHuanxue, born in 1992, M. S. candidate. His research interests include computer network.

ZHOUQianhao, born in 1997. His research interests include high performance computing.