海洋樁基水動力系數的確定方法研究

(山東科技大學 山東 青島 266590)

1 引言

樁基結構是海洋風電基礎中適用于近海海域的結構形式[1]。在樁基穩定性計算中，基樁的波浪力計算至關重要。目前計算小直徑樁的波浪力一般采用莫里森方程，其中的關鍵是合理確定慣性力系數CM和拖曳力系數CD[2]。目前確定CM和CD的主要有三種，一是利用瞬時值計算數CM和CD，二是利用傅里葉分析法計算CM和CD，三是利用最小二乘法計算CM和CD。本文就針對這三種計算方法并結合《海港水文規范》[3]以及美國API中所規定的CM和CD，分析這幾種方法的優劣。

2 慣性力系數CM和拖曳力系數CD的確定

2.1 瞬時值計算CM和CD。根據線性波理論，當cosωt=0時，速度u=0，加速度a有極值，利用該瞬時波浪力資料可計算CM值；當sinωt=0時，加速度a=0，速度u有極值，利用該瞬時波浪力資料可計算CD的值。

這種方法雖然計算簡單，但必須保證所取瞬時資料的速度及加速度兩個量中，一個值為極值，同時另一個為0.由于波浪的非線性效應，這一條件不一定能夠成立。此外，還應考慮觀測資料的某些不規律性。為了減小這種不規律性對結果所造成的誤差，有時對此瞬時附近的一個小時段取多個值，分析后進行平均。

2.2 傅里葉分析法計算CM和CD。在穩定流中，試驗證明CM和CD為雷諾數Re的函數，而在波浪運動中雷諾數是呈周期性變化的。美國的Keulegan和Carpenter發現系數CM和CD與拖曳力和慣性力的比值有關，并定義KC數為

式中Umax為波浪水質點運動的最大速度；T為波的周期。

目前人們大多認為在波動水流中系數CM和CD是與Re以及KC兩個參數有關。

Keulegan和Carpenter提出由于在波浪水流中流速及加速度兩值均隨時間而周期性地變動，則CM和CD也應在一個周期中統一地加以考慮，即可以在一個周期中用傅里葉分析法來取平均值，該值稱為傅里葉分析均值。他們認為波浪力應為一奇函數，即半周期內異號，則：

+ B1cosθ + B3cos3θ + B5cos5θ + …)

改寫成與莫里森方程相對應的表達式可得到：

-CD|cosθ|cosθ + 2(B3cos3θ + B5cos5θ + …)

如果僅取和莫里森方程相同的項可得：

應特別指出的是，在此認為CM和CD與相位角θ無關，在雷諾數Re和KC數已知時為一常數，且當n>3時，An和Bn各項均為0。

將(1)式的等號兩側各乘以cosθ并對θ在(0,2π)的范圍內積分可得

將(1)式的等號兩側各乘以sinθ并對θ在(0,2π)的范圍內積分可得

由上述兩式就可求得按傅里葉分析法所得的CM和CD的均值。另外也可根據最小二乘法原理，采用該種方法對CM和CD進行計算，此時所選用的CM和CD值應該符合以下條件：E2對CM和CD微分為0。

2.3 各國規范對CM和CD的建議值。美國API規定為：CD為0.6～1.0，CM為1.5～2.1；《海港水文規范》規定為：CD為1.2，CM為2.0；挪威DNV規定為： CD為0.5～1.0，CM為2.0；美國DTI規定為采用可靠的試驗結果。

從上述數據可以看出，各國對CM和CD的定義不盡相同，美國API針對桿件粗糙和光滑，定義了不同的CM和CD值，國內并沒有針對圓柱光滑度的規定，取值相對來說比較保守。最小二乘法(又稱最小平方法)是一種數學優化技術。它通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據，并使得這些求得的數據與實際數據之間誤差的平方和為最小，最小二乘法也可用于參數的計算。

3 波浪要素的計算

3.1 水質點的速度和加速度的計算方法.

(1)海浪譜。隨機波浪與頻率的選取有著較為密切的關系，頻率和波高、波浪頻率等波浪特征值有密切的聯系。實用海上波譜材料為根據大量實測數據統計繪制的。擬合相應的隨機波浪荷載是為了反映相類似的真實環境中海浪的情況。為了反映工程中海上風機所受的實際波浪力而在此采用我國的海浪譜——會戰譜[6]。其形式如下：

上式中：ω為圓頻率；HS為隨機波浪有效波高。

(2)波面方程。將波浪視為平穩隨機過程，假定其是由多個頻率不同、振幅不同、波數不同、初始隨機相位不同的線性波組成的，文中認為隨機波浪由若干余弦波擬合形成。任意組成波的形式如下式：

ηi(t)=Aicos(kix-ωit+εi)

式中：η(t)為波面方程；Ai為任一組成波的振幅；ki為任一組成波的波數；ωi為任一組成波的圓頻率；εi為任一組成波的v初始隨機相位，其值平均分布在[0,2π]范圍內。

根據Airy波理論，采用諧波疊加法，則隨機波浪的波面時程方程如下所示：

任意深度d處的速度時程方程和加速度時程方程如下所示：

3.2 波浪力的計算方法。在海洋工程中，計算小直徑樁波浪力時，經常采用Morison方程進行計算。Morison方程是1950年由美國加州大學伯克利分校的Morison等提出的，是一個半理論半經驗公式。該方法認為結構上的波浪力可以分為兩部分，一部分是波浪質點速度所引起的速度力，另一部分是由波浪質點的加速度所引起的慣性力。作用于單位長度樁體上的波浪力表達式如下：

式中各符號含義為：CD為拖曳力系數；CM為慣性力系數；ρ為海水密度；D為單樁直徑。

從上式中我們不難發現拖曳力是非線性的，所以需要通過Borgman L.E方程進行線性化處理。σu是線性化的關鍵，其計算式中積分上下限的取值應參照實際工程。

在實際計算中，可以采用等分頻率法將截斷頻率分段形成若干個不同大小的線性波浪，采用上述參數，通過現行疊加法得到相應的時程方程。

3.3 工程概況

(1)基本概況。上海東海大橋100MW海上風電示范項目工程位于上海市東海大橋東部海域，總裝機容重102MW，安裝34臺華銳風電科技有限公司生產的單擊容量3MW的SL3000離岸型風電機組。樁柱直徑D=1.7m，水深20.6m。

(2)水文特征。潮位特征(國家85高程)為：平均海平面為0.23米，平均高潮面為1.86米，平均低潮面為-1.34米，設計高潮面為2.55米，設計低潮面為-2.09米，極端高潮面為3.68米，極端低潮面為-2.93米。

設計波浪要素為：重現期為50年，平均波高為2.83米，平均周期長為7.76秒，波長為74.1米，H1%為5.81米，，H4%為5.06米，H5%為4.92米，H13%為4.24米。

4 計算結果分析

從會戰譜曲線圖中我們可以看出，譜值在圓頻率達到2.5以后的變化量幾乎很小，所以取0.2<ω<2.5范圍內進行計算。與此同時，我們還可以采用3.1中的計算方法，求得波面方程時程曲線。

由瞬時值法、傅里葉分析法、最小二乘法和《海港水文規范》、美國API確定的CM和CD如表4所示。

表4 CM和CD取值

CDCM規范法1.22最小二乘法0.581.42傅里葉分析法0.621.56瞬時值法0.811.12

據上述幾種方法確定的CM和CD，代入Morison方程計算得到的單位高度上的波浪力時程曲線，如圖5所示。

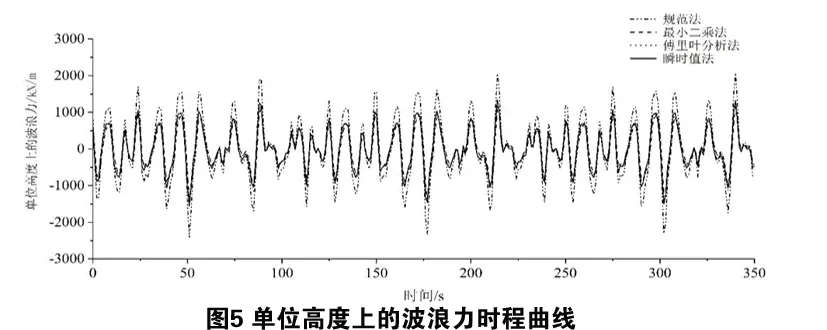
從圖中我們可以看出，瞬時值法和《海港水文規范》確定的CM和CD值偏差較大，而通過傅里葉分析法和最小二乘法計算得到的CM和CD值比較接近且更為合理。

5 結論

由瞬時值法計算得到的CM和CD值，由于其計算取值的條件過于苛刻，而實際情況并不十分符合計算原理，所以得到的計算結果誤差較大。而《海港水文規范》中所規定的CM和CD值的取值相對比較保守，根據國內規范計算得出的拖曳力和慣性力較大。傅里葉分析法和最小二乘法計算得到的CM和CD值比較合理，在實際工程中可以根據已有的波浪數據選擇適合的方法進行計算。