柱形生物質(zhì)和石英砂傳熱實(shí)驗(yàn)與模擬研究

郭飛宏 王澤宇 仲兆平

(1.東南大學(xué)能源與環(huán)境學(xué)院，南京 210096; 2.能源熱轉(zhuǎn)換及其過(guò)程測(cè)控教育部重點(diǎn)實(shí)驗(yàn)室，南京 210096)

柱形生物質(zhì)和石英砂傳熱實(shí)驗(yàn)與模擬研究

郭飛宏1,2王澤宇1,2仲兆平1,2

(1.東南大學(xué)能源與環(huán)境學(xué)院，南京 210096; 2.能源熱轉(zhuǎn)換及其過(guò)程測(cè)控教育部重點(diǎn)實(shí)驗(yàn)室，南京 210096)

從實(shí)驗(yàn)和模擬兩方面，利用虛擬球元法改進(jìn)傳統(tǒng)的計(jì)算流體力學(xué)耦合離散單元法(DEM-CFD)，對(duì)流化床內(nèi)的柱形生物質(zhì)和石英砂的流動(dòng)傳熱過(guò)程進(jìn)行了研究。建立了混合流動(dòng)與傳熱的實(shí)驗(yàn)系統(tǒng)，并進(jìn)行了模擬和分析，結(jié)果表明：雙組分顆粒混合指數(shù)(MI)經(jīng)過(guò)迅速增加、緩慢增加以及穩(wěn)定期3個(gè)階段。隨著表觀氣速的增加，顆粒混合指數(shù)升高，一定范圍內(nèi)的高氣速有利于柱形生物質(zhì)和石英砂的混合。加熱后的柱形生物質(zhì)和石英砂的初始溫度為120℃，流化空氣為常溫25℃。流化過(guò)程中，柱形生物質(zhì)顆粒溫度普遍大于石英砂的溫度。當(dāng)表觀氣速比較小時(shí)，雙組分顆粒的混合受到限制，流化床內(nèi)不同高度的顆粒平均溫度差較大；表觀氣速較大時(shí)，流化床顆粒平均溫度差不明顯。虛擬球元解決了傳統(tǒng)DEM-CFD計(jì)算模型不適用于大尺寸柱形顆粒系統(tǒng)的問(wèn)題。對(duì)比紅外熱圖像和模擬結(jié)果，實(shí)驗(yàn)值和模擬結(jié)果比較接近，改進(jìn)的DEM-CFD方法可以較好地模擬柱形生物質(zhì)和石英砂的流動(dòng)傳熱。

柱形生物質(zhì)； 石英砂； 傳熱； 實(shí)驗(yàn)； 模擬

引言

流化床中的氣固流動(dòng)屬于高濃度的流態(tài)化過(guò)程，具有高強(qiáng)度的熱量、質(zhì)量和動(dòng)量傳遞的優(yōu)點(diǎn)。流化床技術(shù)作為生物質(zhì)熱解或直接燃燒的主要技術(shù)，其內(nèi)部流動(dòng)復(fù)雜程度極高，成為氣固兩相流領(lǐng)域研究的熱點(diǎn)。相比實(shí)驗(yàn)研究，數(shù)值模擬能通過(guò)狀態(tài)參數(shù)設(shè)置快速方便地反映稠密相流動(dòng)和傳熱狀態(tài)，因此成為研究流化床流動(dòng)及傳熱的主要方法之一[1-3]。但由于數(shù)值計(jì)算方法采用了簡(jiǎn)化或抽象的模型來(lái)模擬真實(shí)條件下的流動(dòng)，其結(jié)果需要實(shí)驗(yàn)測(cè)量進(jìn)行定性或定量的驗(yàn)證。

TSUJI等[4]提出將DEM和CFD耦合的DEM-CFD方法后，在歐拉-拉格朗日框架中的氣固流動(dòng)模擬計(jì)算取得了長(zhǎng)足的發(fā)展。FENG等[5]基于DEM-CFD對(duì)由不同尺寸不同密度組成的雙組分顆粒的流化、混合及分離過(guò)程進(jìn)行了模擬。DI RENZO等[6]基于DEM-CFD對(duì)流化床中2種具有相同直徑但密度不同的雙組分顆粒進(jìn)行了模擬。在傳熱過(guò)程的流化床中，一些研究者也嘗試將DEM-CFD方法與傳熱模型相耦合[7-9]。傳統(tǒng)DEM方法只適用于球形顆粒，然而在實(shí)際過(guò)程中，生物質(zhì)流化床中不僅僅有規(guī)則的球形顆粒，還有很多的異形顆粒，并且尺度都較石英砂大，對(duì)于這類問(wèn)題的模擬，傳統(tǒng)的DEM-CFD方法往往無(wú)能為力。基于此，研究者對(duì)傳統(tǒng)的DEM-CFD方法進(jìn)行了擴(kuò)展研究，使之能夠適用于非球形顆粒流動(dòng)的模擬[10-11]。

本文從實(shí)驗(yàn)和模擬兩方面，采用DEM-CFD和虛擬球元法對(duì)柱形生物質(zhì)-石英砂雙組分流化床流動(dòng)及傳熱進(jìn)行模型建立、驗(yàn)證。為檢驗(yàn)?zāi)M結(jié)果的準(zhǔn)確性，搭建可視化-透紅外流化床實(shí)驗(yàn)臺(tái)，通過(guò)分析流化床內(nèi)顆粒混合指數(shù)、顆粒運(yùn)動(dòng)和溫度分布，以期揭示流化床雙組分流動(dòng)與傳熱的規(guī)律。

1 流動(dòng)和傳熱的基本理論

采用虛擬球元法來(lái)處理柱形顆粒的受力作用。在氣固曳力耦合方面采用改進(jìn)后的Ergun和Wen & Yu氣固曳力模型[12-13]，在氣固傳熱耦合方面采用等效直徑法改進(jìn)傳統(tǒng)Gunn對(duì)流傳熱公式。

1.1 改進(jìn)的氣固作用力

氣固兩相流動(dòng)中的氣相微分方程與單相流相似，但由于單個(gè)計(jì)算網(wǎng)格內(nèi)存在固體顆粒，因此必須引入氣相空隙率來(lái)考慮單位網(wǎng)格內(nèi)固體所占體積比例的影響。氣相連續(xù)相方程為

(1)

式中ε——單位網(wǎng)格空隙率，其值等于單位網(wǎng)格內(nèi)氣體所占的體積比例

ρf——?dú)怏w密度τ——應(yīng)力張量

uf——?dú)庀嗨矔r(shí)速度矢量

將柱形顆粒視為由緊密排列的單一尺寸虛擬小球組成。作為模型參數(shù)定義虛擬球的直徑為dfic，定義虛擬小球占柱形顆粒的體積分?jǐn)?shù)為afic。這樣如果dfic足夠小而afic足夠大，虛擬小球的聚團(tuán)就可以被視為大尺寸實(shí)心顆粒。則空隙率ε就可以表示為

ε=1-ap-asafic

(2)

式中ap——單位網(wǎng)格內(nèi)小尺寸顆粒的體積分?jǐn)?shù)

as——單位網(wǎng)格內(nèi)柱形顆粒的體積分?jǐn)?shù)

氣相動(dòng)量方程為

(3)

其中

(4)

式中p——當(dāng)?shù)貧庀嗥骄鶋毫?/p>

f——?dú)夤桃妨?/p>

β——?dú)夤桃妨ο禂?shù)

Np——單個(gè)網(wǎng)格內(nèi)石英砂顆粒個(gè)數(shù)

Nfic——單個(gè)網(wǎng)格內(nèi)虛擬顆粒的個(gè)數(shù)

Vp——單個(gè)石英砂顆粒體積

Vfic——單個(gè)虛擬顆粒體積

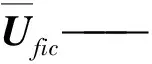
常用的曳力模型有Ergun模型、Wen & Yu模型[14]和Gibilaro模型[15]等。本研究中，根據(jù)空隙率的不同分別采用Ergun和Wen & Yu表達(dá)式計(jì)算，即

(5)

μf——?dú)庀嗾扯萊e——雷諾數(shù)

CD——流場(chǎng)內(nèi)單顆粒曳力系數(shù)

1.2 改進(jìn)的氣固對(duì)流換熱

氣固對(duì)流換熱Qf-p受到氣固兩相溫度差和對(duì)流傳熱系數(shù)的影響[16-17]，其表達(dá)式為

(6)

其中

βT=Nukf/dp

(7)

式中Qf-p——?dú)庀嗯c顆粒相對(duì)流換熱量

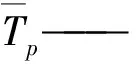
Sp——顆粒表面積Tf——流體溫度

βT——對(duì)流換熱系數(shù)

kf——?dú)庀鄬?dǎo)熱系數(shù)

dp——網(wǎng)格內(nèi)的顆粒平均直徑

Nu——Nusselt數(shù)

結(jié)合虛擬球元法的思想，把每個(gè)氣體和柱形生物質(zhì)的對(duì)流換熱看成是每個(gè)虛擬球元與氣體的對(duì)流換熱。通過(guò)直接數(shù)值模擬的方法比較，得知采用等效直徑和球形度表示的修正Gunn公式在模擬非球形顆粒時(shí)具有一定的準(zhǔn)確性[18-19]。等效直徑方法表達(dá)式為

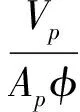
(8)

式中Ap——柱形顆粒的表面積

φ——圓球度，定義為等表面積的球體積與柱形顆粒體積的比值

本研究基于Gunn模型，Nu的計(jì)算式為

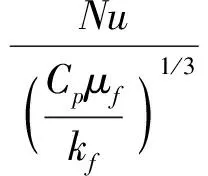
(1.33-2.4ε+1.2ε2)Re0.7

(9)

式中Cp——固體顆粒比熱容

2 實(shí)驗(yàn)系統(tǒng)及模型建立

2.1 實(shí)驗(yàn)系統(tǒng)

生物質(zhì)與石英砂混合流動(dòng)與傳熱實(shí)驗(yàn)裝置如圖1所示。實(shí)驗(yàn)裝置主要包括流化床主體、供風(fēng)系統(tǒng)、加熱系統(tǒng)、數(shù)據(jù)采集系統(tǒng)以及圖像采集系統(tǒng)。流化空氣為常溫空氣，研究熱顆粒(加熱后的顆粒)隨時(shí)間的冷卻情況和在流化床內(nèi)的流動(dòng)狀態(tài)。加熱后的顆粒初始溫度為120℃，流化空氣為常溫25℃。紅外熱像儀用來(lái)記錄顆粒溫度隨時(shí)間的變化情況，高速攝影儀用來(lái)記錄不同時(shí)間點(diǎn)的流動(dòng)狀態(tài)。實(shí)驗(yàn)測(cè)量所得的數(shù)據(jù)將為后續(xù)模擬結(jié)果的檢驗(yàn)提供依據(jù)。

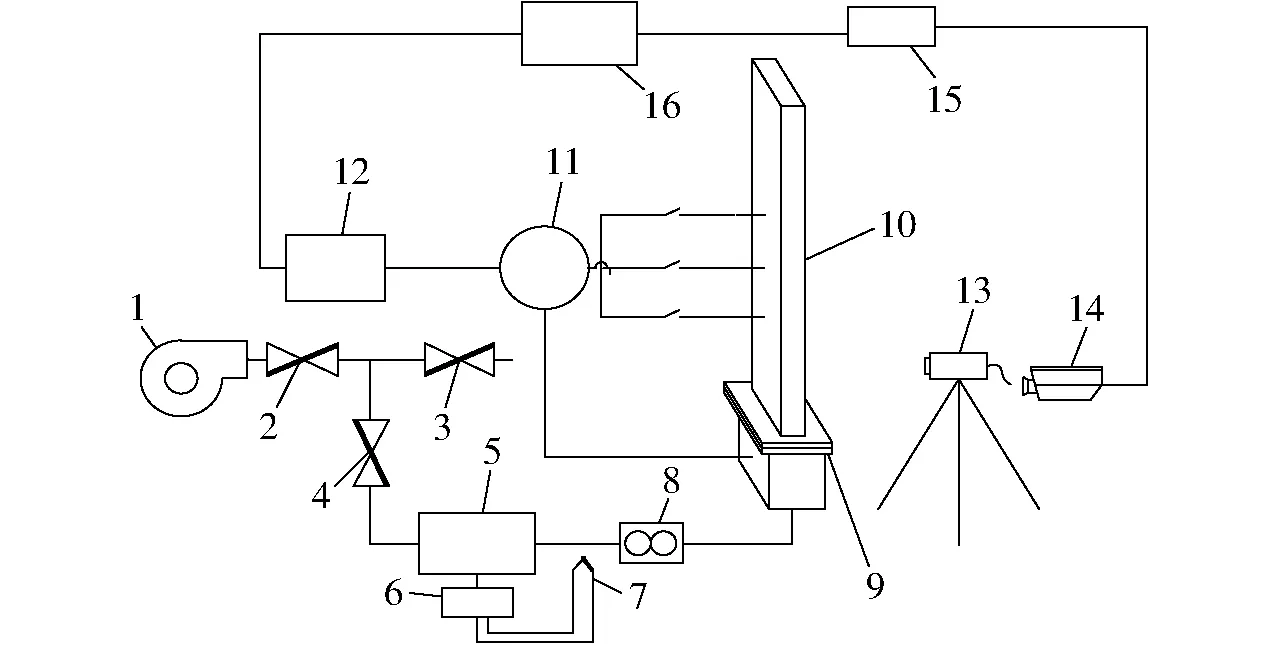
圖1 流化床實(shí)驗(yàn)系統(tǒng)Fig.1 Schematic diagram of fluidized bed system1.鼓風(fēng)機(jī) 2.總閥 3.放空閥 4.控制閥 5.氣體加熱器 6.溫控箱 7.熱電偶 8.轉(zhuǎn)子流量計(jì) 9.布風(fēng)板 10.流化床11.差壓變送器 12.USB數(shù)據(jù)采集器 13.高速攝影儀 14.紅外熱像儀 15.路由器 16.計(jì)算機(jī)

按照生物質(zhì)質(zhì)量分?jǐn)?shù)計(jì)算并取用實(shí)驗(yàn)所需的一定數(shù)量生物質(zhì)顆粒，并與石英砂混合后放入電加熱爐中加熱至顆粒初始溫度，保持1～2 h以使柱形生物質(zhì)顆粒內(nèi)部溫度分布均勻后迅速加入流化床中，同時(shí)調(diào)節(jié)流量計(jì)旋鈕使表觀氣速達(dá)到工況要求。分別用高速攝影儀和紅外熱像儀采集流化顆粒流動(dòng)狀態(tài)圖像和顆粒溫度分布。

2.2 實(shí)驗(yàn)材料

實(shí)驗(yàn)所用物料如表1所示，其中比熱容和導(dǎo)熱系數(shù)為KD2Pro型熱特性分析儀(美國(guó)DECAGON)測(cè)定10個(gè)樣品的平均值。

表1 實(shí)驗(yàn)材料性質(zhì)Tab.1 Properties of experimental material

2.3 物理模型

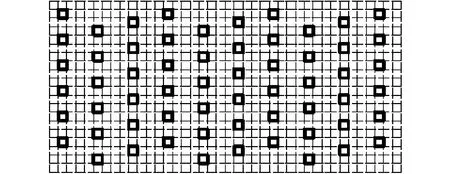
圖2 布風(fēng)板噴口設(shè)置Fig.2 Schematic diagram of air distribution plate

初始布置時(shí)，石英砂顆粒松散堆積于生物質(zhì)顆粒下部，柱形顆粒之間、柱形顆粒與石英砂之間存在著一定間隙，在布風(fēng)板氣流進(jìn)入床內(nèi)前，顆粒有1 s的時(shí)間自由下落成緊密堆積形式。本模擬中布風(fēng)板開(kāi)孔布置如圖2所示，布風(fēng)板尺寸為床體截面尺寸(80 mm×40 mm)，共開(kāi)有60個(gè)方形小孔，其開(kāi)孔率為5%。圖中粗實(shí)線代表布風(fēng)板噴口處，其余部分均為平壁面，每個(gè)網(wǎng)格尺寸為2 mm×2 mm，上下相鄰開(kāi)孔距離為4 mm，左右相鄰兩排噴口間距也為4 mm。實(shí)踐證明如噴口過(guò)于接近四周壁面，則會(huì)引起計(jì)算過(guò)程的發(fā)散，且會(huì)發(fā)生床內(nèi)顆粒超出邊界造成計(jì)算錯(cuò)誤，因此布風(fēng)板四周靠近壁面處都不設(shè)置噴口。模擬計(jì)算中，壁面采用無(wú)滑移邊界條件。入口邊界采用速度入口邊界條件，布風(fēng)板上氣孔內(nèi)設(shè)置為速度入口邊界條件，其余部分為壁面無(wú)滑移邊界條件。出口邊界采用常用的壓力出口邊界條件。本研究設(shè)置初始?jí)毫? Pa，初始?xì)庀嗨俣葹? m/s。

3 實(shí)驗(yàn)結(jié)果與討論

3.1 顆粒的混合分析

圖3和圖4為石英砂和柱形生物質(zhì)在不同氣速不同時(shí)刻下的混合情況。可見(jiàn)，柱形生物質(zhì)主要存在于中上部分的床層區(qū)域，在氣泡聚并并發(fā)生破碎時(shí)，一部分被抬高的生物質(zhì)穿過(guò)中間床層的空隙回落到中、低床層中，后又被周圍的石英砂抬升至床層頂部，以此往復(fù)運(yùn)動(dòng)。當(dāng)表觀氣速v=1.0 m/s時(shí)，顆粒整體膨脹高度較小，此時(shí)的柱形生物質(zhì)主要聚集在流化床的上部，雙組分的混合程度不是很好。當(dāng)表觀氣速v=1.5 m/s時(shí)，顆粒整體膨脹高度較大。t=0.5 s時(shí), 床料被噴口產(chǎn)生的高速氣體整體抬升至100 mm的高度。t=2.0 s時(shí),中間位置生成了大而明顯的氣泡，隨即便向上匯合并最終在頂層破裂。t為8、10 s時(shí),氣泡破裂，石英砂和生物質(zhì)開(kāi)始回落。當(dāng)表觀氣速v=2.0 m/s時(shí),柱形顆粒和石英砂的流動(dòng)更加劇烈，一方面顆粒的上升高度被進(jìn)一步抬升，另一方面生成更多的氣泡，柱形生物質(zhì)的分布區(qū)間更加廣泛。

圖3 不同氣速下流化床內(nèi)雙組分顆粒流動(dòng)圖Fig.3 Flow diagram of binary particles in fluidized bed at different gas velocities

圖4 不同時(shí)刻流化床內(nèi)雙組分顆粒流動(dòng)圖(v=1.5 m/s)Fig.4 Flow diagram of binary particles in fluidized bed at different time (v=1.5 m/s)

通過(guò)雙組分顆粒流動(dòng)圖像，分析了流化床流動(dòng)的混合效果。但在混合過(guò)程的中后期，肉眼已經(jīng)很難辨別混合效果的差距，因此合理準(zhǔn)確定量分析混合效果的方法顯得尤其必要，Lacey混合指數(shù)I[20]能有效克服標(biāo)準(zhǔn)偏差的缺點(diǎn)。其表達(dá)式如下

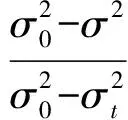
(10)

其中

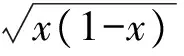
(11)

(12)

式中σ——實(shí)際混合時(shí)的標(biāo)準(zhǔn)差

σ0——完全分離時(shí)的標(biāo)準(zhǔn)差

x——某一顆粒在樣本中所占的比例

N——取樣網(wǎng)格中平均樣本數(shù)

σt——完全隨機(jī)混合時(shí)的標(biāo)準(zhǔn)差

圖5為不同表觀氣速下顆粒混合指數(shù)隨時(shí)間的變化曲線。可以看出，不同氣速下柱形生物質(zhì)和石英砂的混合指數(shù)基本上經(jīng)歷了迅速增加期、緩慢增加期以及穩(wěn)定期3個(gè)階段。v=1.0 m/s時(shí)，床料混合指數(shù)首先在1 s內(nèi)，由0迅速增至0.4，隨后在1～1.5 s的時(shí)間內(nèi)基本維持不變，在1.5～2.0 s內(nèi)混合指數(shù)又迅速增至0.56左右，之后維持在0.56左右。表觀氣速v=1.5 m/s時(shí)，0～1.0 s為混合指數(shù)的迅速增加期，I從0增至了0.60，隨后在1.5～2.0 s內(nèi)進(jìn)入到了緩慢增加期，在2.0～3.0 s內(nèi)混合指數(shù)在0.64左右上下波動(dòng)。v=2.0 m/s時(shí)，混合指數(shù)數(shù)值明顯比較高，最終穩(wěn)定在0.72左右。不同表觀氣速下，由混合指數(shù)變化規(guī)律可知，較高的表觀氣速有利于柱形生物質(zhì)和石英砂的混合。

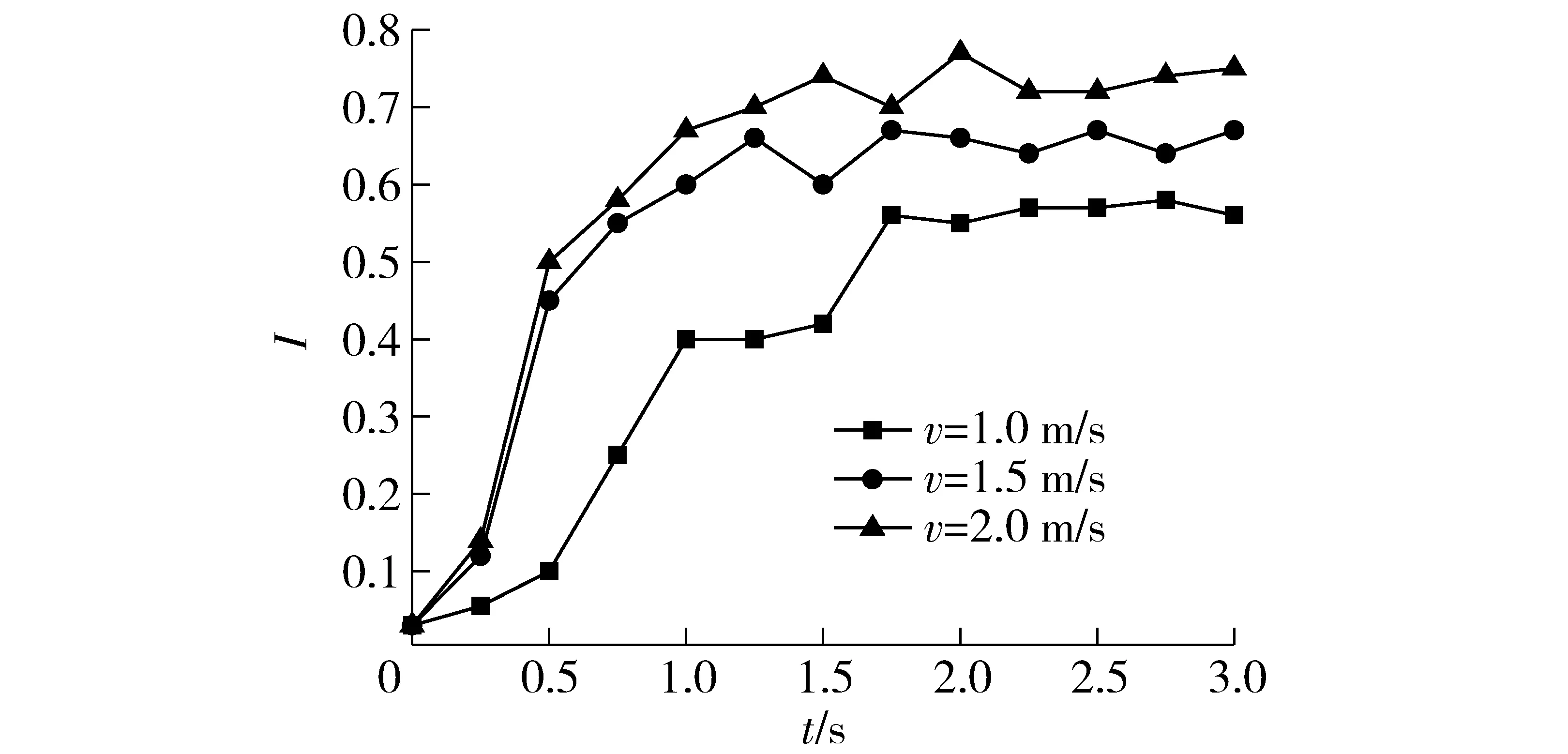
圖5 不同氣速下混合指數(shù)隨時(shí)間的變化曲線Fig.5 Variation curves of mixing index with time at different gas velocities

3.2 紅外熱圖像溫度分析

不同時(shí)刻和速度下，生物質(zhì)質(zhì)量分?jǐn)?shù)為10%的顆粒熱紅外溫度分布如圖6、7所示。由圖6可知，當(dāng)t=1 s時(shí)流化床內(nèi)的顆粒溫度分布不太均勻，床層底處的顆粒(h=20 mm)受到常溫空氣的冷卻，溫度低于高床層處(h=80 mm)的溫度。隨著表觀氣速的增加，這種溫度的不均勻性有一定程度的減小。隨著時(shí)間的增加，顆粒的溫度逐漸降低。當(dāng)t=20 s時(shí)，中床層(h=50 mm)的顆粒溫度相對(duì)較高，這主要是因?yàn)橹紊镔|(zhì)主要分布在中床層處，柱形生物質(zhì)的溫度高于石英砂的溫度。由于生物質(zhì)比熱較大，且表面?zhèn)鳠嵯禂?shù)較小，同時(shí)也由于單個(gè)生物質(zhì)質(zhì)量較大，溫度下降得較慢。圖7中較高的波峰主要是生物質(zhì)顆粒存在的區(qū)域，整體來(lái)看，中間床層的溫度較高，隨著時(shí)間的變化，高床層的溫度變化較大，中低床層的溫度趨于均勻，而低床層的溫度普遍低于中間床層的溫度。同時(shí)，靠近壁面的顆粒溫度也偏低。

圖6 顆粒的熱紅外溫度分布(t=1 s)Fig.6 Infrared temperature distribution of particles (t=1 s)

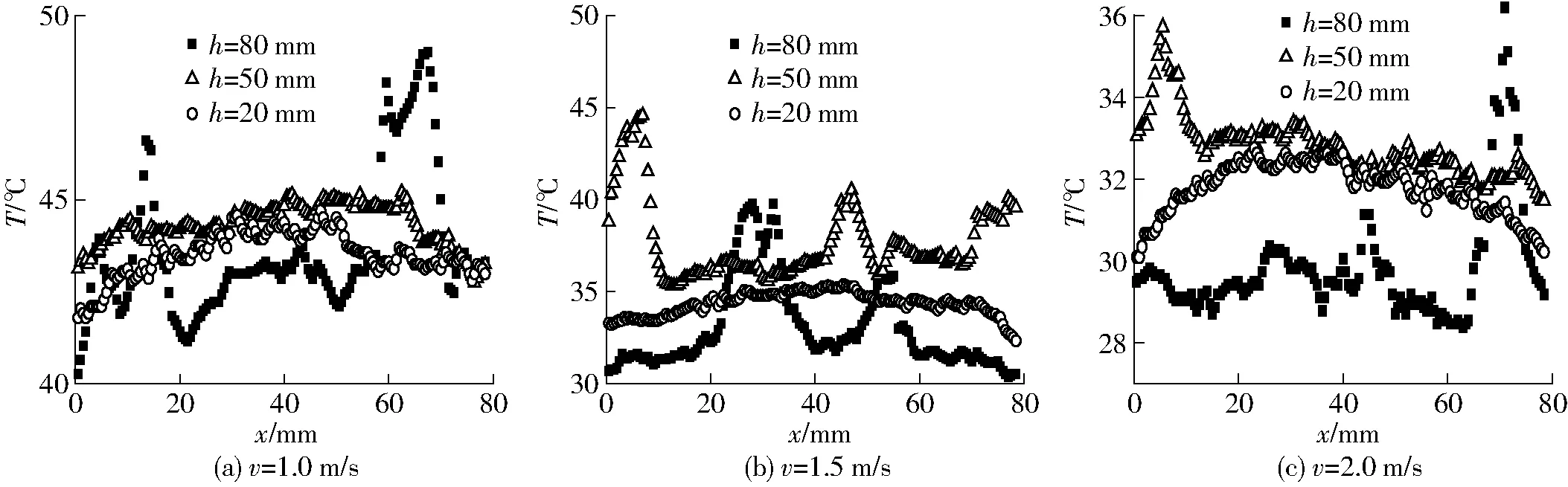
圖7 顆粒的熱紅外溫度分布(t=20 s)Fig.7 Infrared temperature distribution of particles (t=20 s)

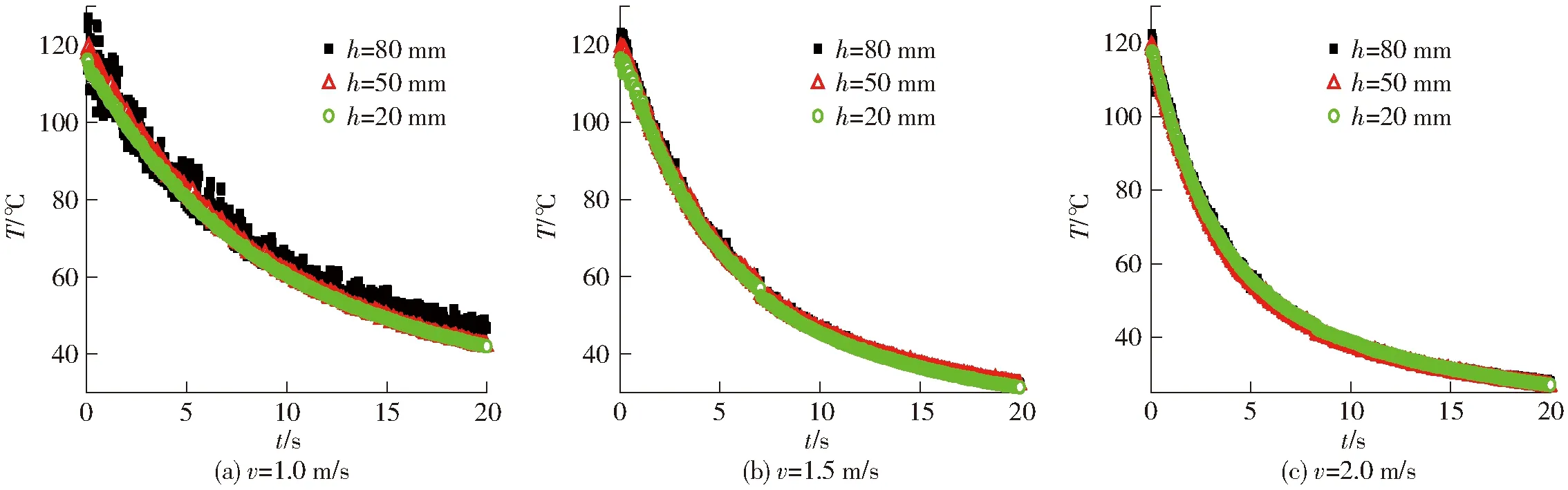
圖8 不同氣速下顆粒溫度隨時(shí)間的變化曲線Fig.8 Variation curves of particle temperature with time at different gas velocities

圖8為生物質(zhì)質(zhì)量分?jǐn)?shù)為15%的工況下，不同氣速條件下的顆粒平均溫度隨著時(shí)間的變化曲線。流化床內(nèi)床料溫度隨著時(shí)間的推移，下降速度逐漸降低。表觀氣速對(duì)流化床溫度的影響較為明顯。由圖8可以看出當(dāng)表觀氣速為1.0、1.5、2.0 m/s時(shí)，床內(nèi)流化開(kāi)始后0～3 s的時(shí)間內(nèi)床料平均溫度從120℃分別下降到了95℃、83℃、73℃；床內(nèi)流化開(kāi)始后0～20 s的時(shí)間內(nèi)床料平均溫度分別下降到了42℃、33℃、29℃。可見(jiàn)，當(dāng)表觀氣速比較大時(shí)，流化床內(nèi)的顆粒平均溫度降幅比較大。當(dāng)v=1.0 m/s時(shí)，床內(nèi)生物質(zhì)與石英砂混合情況并不理想，導(dǎo)致大部分生物質(zhì)顆粒在最高床層區(qū)域運(yùn)動(dòng)，在平均溫度趨勢(shì)圖中則表現(xiàn)為：高床層區(qū)域的顆粒平均溫度明顯高于其他2個(gè)床層高度下的顆粒平均溫度，并且平均溫度產(chǎn)生較大幅度的震蕩。t=20 s，v=1.0 m/s時(shí)，h=80 mm處的顆粒平均溫度為50℃，比其他床層高度的顆粒平均溫度高5～8℃，這說(shuō)明生物質(zhì)顆粒的冷卻速度明顯小于石英砂顆粒。而v=1.5 m/s和v=2.0 m/s時(shí)，由于床內(nèi)氣泡數(shù)量較多，尺寸較大，生物質(zhì)能夠充分與氣泡接觸，床內(nèi)物料混合較劇烈，使得各床層高度下的床料溫差并不明顯。

3.3 模擬值和實(shí)驗(yàn)值的對(duì)比

圖9、10給出了不同表觀氣速下，顆粒溫度和位置分布隨時(shí)間變化的模擬情況。從床層高度、床內(nèi)顆粒和氣泡運(yùn)動(dòng)狀態(tài)等方面，對(duì)比模擬結(jié)果與高速攝影儀拍攝的顆粒瞬時(shí)運(yùn)動(dòng)狀態(tài)圖像，可以看出模擬結(jié)果與實(shí)際工況具有一定的相似度。當(dāng)v=1.5 m/s和v=2.0 m/s時(shí)，床內(nèi)產(chǎn)生了較為強(qiáng)烈的氣固換熱，由于布風(fēng)板噴口處氣體溫度較低，床層底部區(qū)域顆粒溫度較低，床層中間低溫氣泡周圍的也存在著少量低溫石英砂顆粒。由于柱形生物質(zhì)具有大尺寸、大比熱、低導(dǎo)熱率等特點(diǎn)，溫度下降緩慢，總體上柱形生物質(zhì)溫度比石英砂更高。當(dāng)t=0.5 s時(shí)床內(nèi)生物質(zhì)顆粒均在125℃，大部分石英砂的溫度也在120～125℃之間，但靠近壁面處的石英砂顆粒溫度較低，在105～115℃之間，布風(fēng)板上部的顆粒溫度在105～110℃之間。當(dāng)時(shí)間進(jìn)行到2 s時(shí)，床料被抬升至150 mm高度。柱形生物質(zhì)溫度下降至100～110℃，床內(nèi)石英砂降為95℃左右，壁面處的石英砂溫度為85～90℃。當(dāng)t=10 s時(shí)，床料溫度下降至25～40℃之間，生物質(zhì)溫度較大，在50～60℃之間。氣速較高時(shí)，溫度下降的趨勢(shì)更加明顯。

圖11和圖12為表觀氣速v=1.5、2.0 m/s時(shí)不同床層高度顆粒平均溫度隨時(shí)間變化的實(shí)驗(yàn)值和模擬值變化曲線。實(shí)驗(yàn)過(guò)程中，由于雙組分顆粒的混合作用，顆粒平均溫度會(huì)在較短時(shí)間內(nèi)上下波動(dòng)，但整體呈現(xiàn)下降的趨勢(shì)，且溫度下降的速度隨時(shí)間的增加而逐漸減緩。模擬時(shí)，當(dāng)表觀氣速v=1.5 m/s時(shí)，經(jīng)過(guò)8 s后，顆粒平均溫度從120℃下降至50℃左右，其中顆粒(h=40 mm, 60 mm)的平均溫度比較接近，而顆粒(h=15 mm)平均溫度比其他位置的溫度低3℃左右。當(dāng)表觀氣速v=2.0 m/s時(shí)，4 s后顆粒平均溫度從120℃下降到了80℃左右。與紅外熱像儀采集的數(shù)據(jù)比較，在t=4、8 s和v=1.5 m/s、2.0 m/s下，模擬值與實(shí)驗(yàn)值的偏差都在10%以內(nèi)，模擬效果較好。但模擬值相對(duì)于實(shí)驗(yàn)值，波動(dòng)更加明顯。這是為了縮短模擬過(guò)程的計(jì)算時(shí)間，避免計(jì)算程序發(fā)散，在模擬工況下石英砂顆粒直徑設(shè)為0.8 mm，數(shù)量最多為20萬(wàn)個(gè)，而在實(shí)驗(yàn)中石英砂顆粒粒徑為0.5 mm。因此實(shí)驗(yàn)中的石英砂顆粒數(shù)量多于模擬程序中的石英砂顆粒，而作為流化介質(zhì)，石英砂顆粒數(shù)量越多，床內(nèi)的顆粒接觸傳熱就越充分，溫度分布就越均勻。

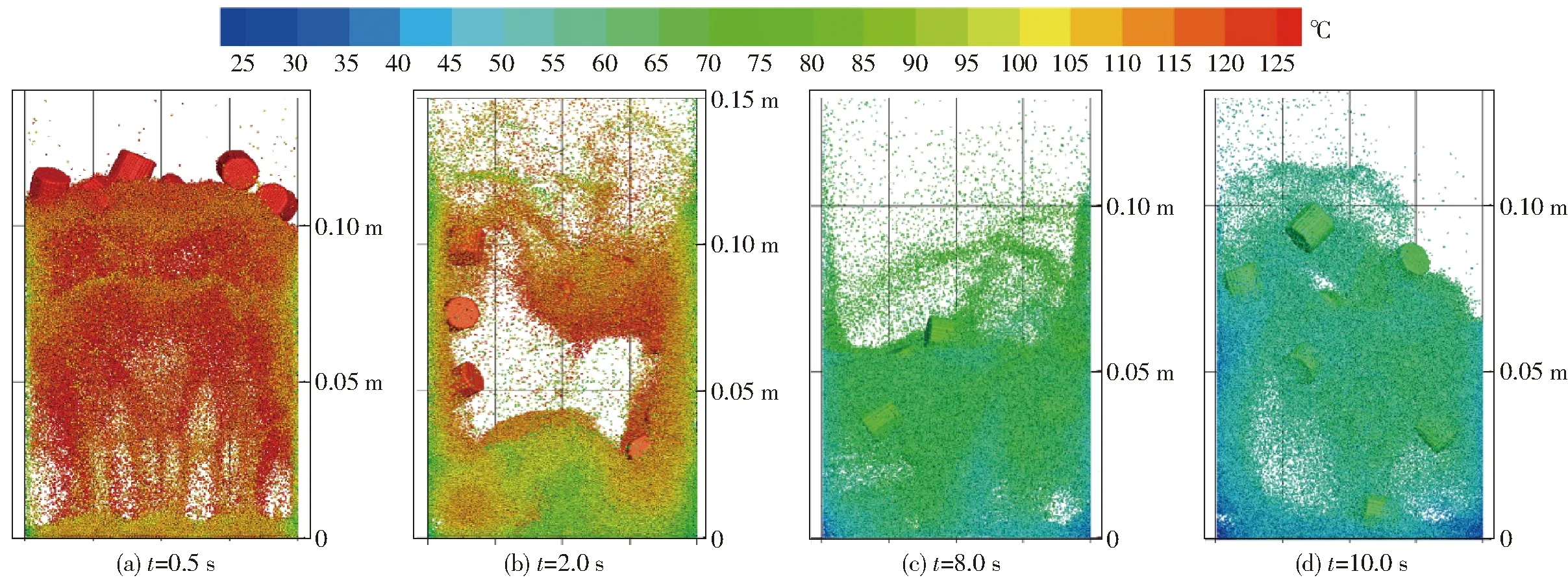
圖9 顆粒位置及溫度分布隨時(shí)間的變化 (v=1.5 m/s)Fig.9 Variation of particle position and temperature distribution with time (v=1.5 m/s)

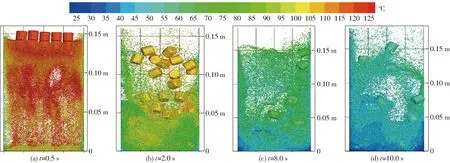
圖10 顆粒位置及溫度分布隨時(shí)間的變化 (v=2.0 m/s)Fig.10 Variation of particle position and temperature distribution with time (v=2.0 m/s)

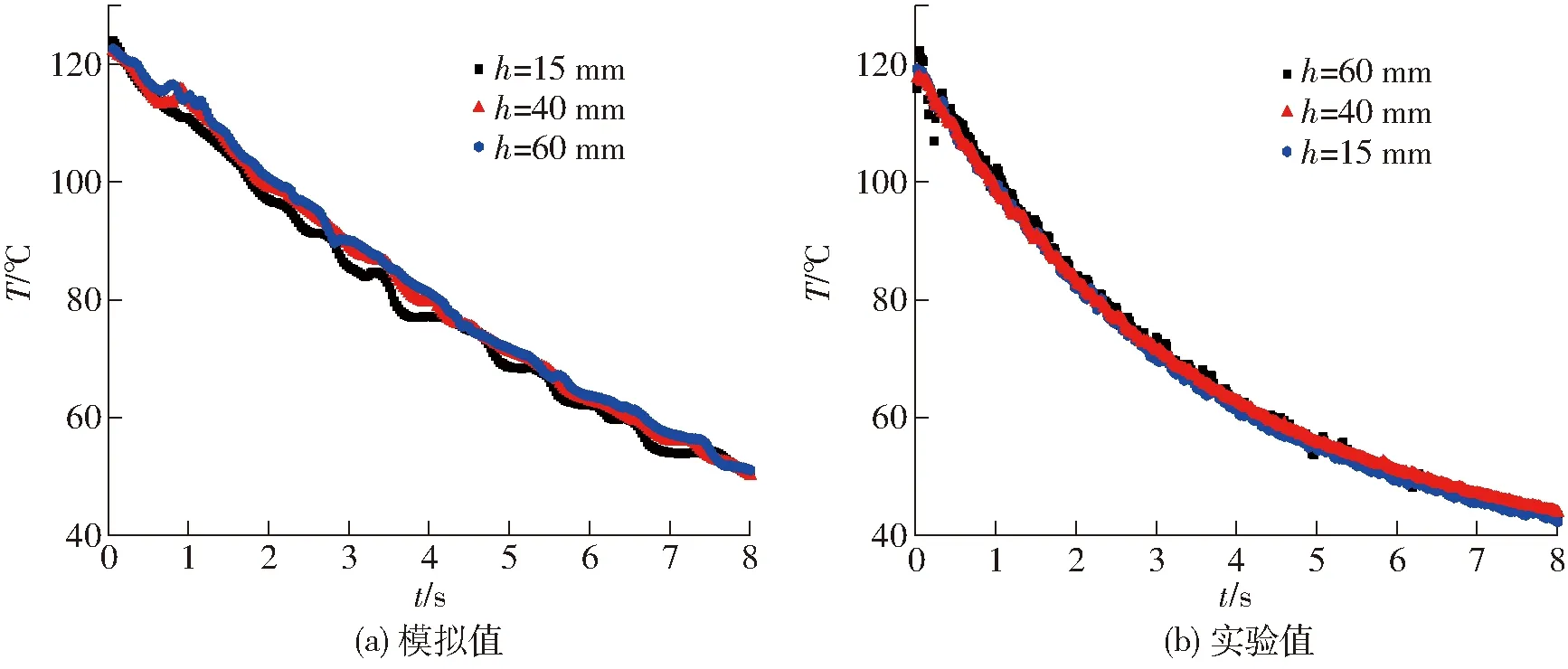
圖11 不同床層高度顆粒平均溫度隨時(shí)間的變化(v=1.5 m/s)Fig.11 Variations of average particle temperature at different bed heights (v=1.5 m/s)

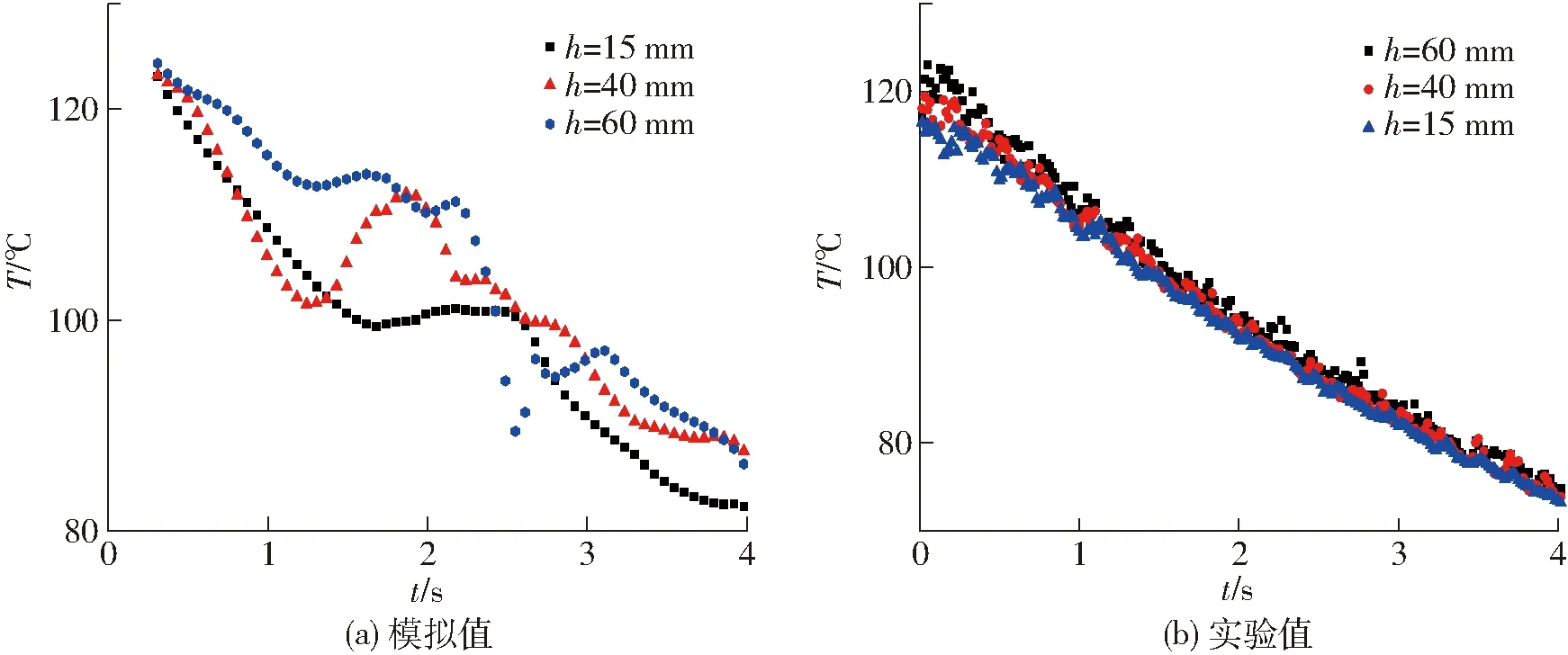
圖12 不同床層高度顆粒平均溫度隨時(shí)間的變化(v=2.0 m/s)Fig.12 Variations of average particle temperature at different bed heights (v=2.0 m/s)

4 結(jié)論

(1)采用混合指數(shù)定量分析了柱形生物質(zhì)和石英砂在流化床中的混合情況，混合指數(shù)經(jīng)過(guò)了迅速增加期、緩慢增加期以及穩(wěn)定期3個(gè)階段。隨著表觀氣速的增加，混合指數(shù)升高，高氣速工況有利于柱形生物質(zhì)和石英砂的混合。

(2)柱形生物質(zhì)顆粒溫度普遍大于石英砂的溫度。當(dāng)表觀氣速比較小時(shí)，雙組分顆粒的混合受到限制，流化床內(nèi)不同高度的顆粒平均溫度差較大；表觀氣速較大時(shí)，流化床各高度下的顆粒平均溫度差并不明顯。

(3)模擬時(shí)，柱形生物質(zhì)的溫度降幅小于石英砂，壁面處的顆粒溫度也較小。實(shí)驗(yàn)值和模擬值比較接近，改進(jìn)的DEM-CFD方法可以較好地模擬柱形生物質(zhì)和石英砂的流動(dòng)傳熱。

1 郭雪巖,柴輝生,晁東海.大顆粒流化床傳熱數(shù)值模擬與氣固傳熱模型比較[J].上海理工大學(xué)學(xué)報(bào), 2012, 34(1): 81-87.

2 李洪昌,李耀明,唐忠.風(fēng)篩式清選裝置振動(dòng)篩上物料運(yùn)動(dòng)CFD-DEM數(shù)值模擬[J/OL].農(nóng)業(yè)機(jī)械學(xué)報(bào), 2012, 43(2):79-84.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1&file_no=20120217&journal_id=jcsam.DOI：10.6041/j.issn.1000-1298.2012.02.017.

LI Hongchang, LI Yaoming, TANG Zhong.Numerical simulation of material motion on vibrating screen of air-and-screen cleaning device based on CFD-DEM [J/OL].Transactions of the Chinese Society for Agricultural Machinery, 2012, 43(2): 79-84.(in Chinese)

3 王維,王璐瑤,許英梅.流化床氛圍下多孔物料干燥傳熱傳質(zhì)的數(shù)值模擬[J].化工學(xué)報(bào),2012,63(4): 1044-1049.

WANG Wei, WANG Luyao, XU Yingmei.Numerical simulation on porous material drying with fluidized bed [J].CIESC Journal, 2012, 63(4): 1044-1049.(in Chinese)

4 TSUJI Y, KAWAGUCHI T, TANAKA T.Discrete particle simulation of two-dimensional fluidized bed[J].Powder Technology, 1993, 77(1): 79-87.

5 FENG Y, XU B, ZHANG S, et al.Discrete particle simulation of gas fluidization of particle mixtures[J].AIchE Journal, 2004, 50(8): 1713-1728.

6 DI RENZO A, DI MAIO F P, GIRIMONTE R, et al.DEM simulation of the mixing equilibrium in fluidized beds of two solids differing in density [J].Powder Technology, 2008, 184(2): 214-223.

7 ZHOU Z, YU A, ZULLI P.Particle scale study of heat transfer in packed and bubbling fluidized beds[J].AIchE Journal, 2009, 55(4): 868-884.

8 郭飛宏,王澤宇,仲兆平.基于球元重建與大渦模擬耦合并行算法的數(shù)值模擬[J].東南大學(xué)學(xué)報(bào):自然科學(xué)版,2017,47(2):283-290.

GUO Feihong, WANG Zeyu, ZHONG Zhaoping.Numerical simulation based on sphere reconstruction and large eddy simulation coupled parallel algorithm [J].Journal of Southeast University:Natural Science Edition, 2017, 47(2):283-290.(in Chinese)

9 劉安源, 劉石.流化床內(nèi)顆粒碰撞傳熱的理論研究[J].中國(guó)電機(jī)工程學(xué)報(bào), 2003, 23(3): 161-165.

LIU Anyuan, LIU Shi.Theoretical study on impact heat transfer between particles in fluidized bed [J].Proceedings of the Chinese Society for Electrical Engineering, 2003, 23(3): 161-165.(in Chinese)

10 REN B, ZHONG W Q, CHEN Y, et al.CFD-DEM simulation of spouting of corn-shaped particles[J].Particuology, 2012, 10(5): 562-572.

11 ZHONG W Q, ZHANG Y, JIN B S, et al.Discrete element method simulation of cylinder-shaped particle flow in a gas-solid fluidized bed [J].Chemical Engineering & Technology, 2009, 32(3): 386-391.

12 ILIUTA I, LARACHI F, GRANDJEAN B.Pressure drop and liquid holdup in trickle flow reactors: improved Ergun constants and slip correlations for the slit model [J].Industrial & Engineering Chemistry Research, 1998, 37(12): 4542-4550.

13 MIANOWSKI A, RADKO T, SIUDYGA T.The reactivity of cokes in Boudouard-Bell reactions in the context of an Ergun model [J].Journal of Thermal Analysis and Calorimetry, 2015, 122(2): 1013-1021.

14 NIVEN R K.Physical insight into the Ergun and Wen & Yu equations for fluid flow in packed and fluidized beds [J].Chemical Engineering Science, 2002, 57(3): 527-534.

15 LETTIERI P, BRANDANI S, YATES J G, et al.A generalization of the Foscolo and Gibilaro particle-bed model to predict the fluid bed stability of some fresh FCC catalysts at elevated temperatures [J].Chemical Engineering Science, 2001, 56(18): 5401-5412.

16 ZHAO Y, JIANG M, LIU Y, et al.Particle-scale simulation of the flow and heat transfer behaviors in fluidized bed with immersed tube[J].AIchE Journal, 2009, 55(12): 3109-3124.

17 DI MAIO F P, DI RENZO A, TREVISAN D.Comparison of heat transfer models in DEM-CFD simulations of fluidized beds with an immersed probe [J].Powder Technology, 2009, 193(3): 257-265.

18 TAVASSOLI H，EAJF P，JAM K.Direct numerical simulation of fluid-particle heat transfer in fixed random arrays of non-spherical particles[J].Chemical Engineering Science, 2015, 129: 42-48.

19 FOTOVAT F, ANSART R, HEMATI M, et al.Sand-assisted fluidization of large cylindrical and spherical biomass particles: experiments and simulation[J].Chemical Engineering Science, 2015, 126: 543-559.

20 李少華，朱明亮，張立棟，等.回轉(zhuǎn)裝置內(nèi)三組元顆粒徑向混合評(píng)價(jià)方法分析[J].化工進(jìn)展, 2013(6): 1224-1229.

LI Shaohua，ZHU Mingliang，ZHANG Lidong, et al.Analysis of three-component radial mixing evaluation methods in rotary retorting [J].Chemical Industry and Engineering Progress, 2013(6): 1224-1229.(in Chinese)

ExperimentandImprovedSimulationonHeatTransferforCylindricalBiomassandQuartzSand

GUO Feihong1,2WANG Zeyu1,2ZHONG Zhaoping1,2

(1.SchoolofEnergyandEnvironment,SoutheastUniversity,Nanjing210096,China2.KeyLaboratoryofEnergyThermalConversionandControl,MinistryofEducation,Nanjing210096,China)

From the two aspects of experiment and simulation, virtual spherical method was used to improve the numerical simulation of the traditional computational fluid dynamics coupling discrete element method (CFD-DEM).The cylindrical particle was regarded as aggregation of small virtual ball, and particle volume factor concept was also introduced to amend the gas-solid force.The gas force acting on the cylindrical particle was calculated through the calculation between gas phase and virtual sphere.The experimental system of flow and heat transfer was established, and the simulation and comparative analysis were also carried out.The mixing index (MI) of the special binary particles was followed by three stages: rapid increase, slow increase and stable phase.With the increase of superficial gas velocity, the mixing index of particles was increased, and the higher gas velocity was favorable for the mixing of the cylindrical biomass and quartz sand.In the experiment of heat transfer, the temperature of cylindrical biomass particles was generally higher than that of quartz sand.When the superficial gas velocity was small, the fluidization of particles was restricted, and the average temperature difference at different heights of fluidized bed was larger.At large gas velocity, the average temperature difference was not obvious.The fictitious element method was employed to solve the incompatibility of the traditional DEM-CFD model.Compared with the infrared thermal images and the simulation results, they were very close and the improved DEM-CFD method can simulate the flow and heat transfer of cylindrical biomass and quartz sand.

cylindrical biomass; quartz sand; heat transfer; experiment; simulation

10.6041/j.issn.1000-1298.2017.10.034

TK6

A

1000-1298(2017)10-0272-08

2017-01-15

2017-03-15

國(guó)家自然科學(xué)基金項(xiàng)目(U13161115、51276040)和東南大學(xué)優(yōu)秀博士學(xué)位論文培育基金項(xiàng)目(YBJJ1644)

郭飛宏(1986—)，男，博士生，主要從事生物質(zhì)與煤的混合燃燒及模擬研究，E-mail: kerry151@126.com

仲兆平(1965—)，男，教授，博士生導(dǎo)師，主要從事固體廢棄物利用研究，E-mail: zzhong@seu.edu.cn