一種修正的Osher通量在高階WCNS中的特性

朱華君， 燕振國， 劉化勇,*， 毛枚良,2

1.中國空氣動力研究與發展中心 空氣動力學國家重點實驗室， 綿陽 621000 2.中國空氣動力研究與發展中心 計算空氣動力研究所， 綿陽 621000

一種修正的Osher通量在高階WCNS中的特性

朱華君1， 燕振國1， 劉化勇1,*， 毛枚良1,2

1.中國空氣動力研究與發展中心 空氣動力學國家重點實驗室， 綿陽 621000 2.中國空氣動力研究與發展中心 計算空氣動力研究所， 綿陽 621000

將一種基于多維修正的Osher通量運用于高階加權緊致非線性格式(WCNS)中，該修正通量主要在垂直于激波面的界面上增加耗散，能夠改善Osher通量的激波捕捉穩定性，同時對邊界層和接觸間斷的分辨率影響非常小。對修正的Osher通量在高階WCNS中的特性進行研究，通過數值模擬測試了基于Osher通量的WCNS的激波穩定性、熱流預測精度、邊界層模擬能力、激波邊界層干擾模擬能力，并與Steger-Warming通量和Roe通量進行了對比。結果表明修正后的Osher通量比Harten修正的Roe通量具有更好的激波捕捉魯棒性，而邊界層、駐點熱流值和激波邊界層干擾的模擬則明顯優于Steger-Warming通量。上述結果說明了基于修正的Osher通量的高階WCNS具有較好的激波捕捉特性、熱流預測精度和邊界層計算能力。

通量； 高階WCNS； 激波穩定性； 熱流計算； 邊界層計算

通量的設計對高階精度激波捕捉格式是非常重要的。高階精度格式為了捕捉激波，一般采用基于特征線理論的迎風型通量，通過其迎風特性引入一定的耗散從而使得激波穩定；而為了模擬精細的流場結構，又要求通量的耗散盡可能地小。所以設計能夠較好地捕捉激波，同時又具有較小耗散的通量是具有一定難度的。迎風型通量通常包括通量差分型通量和通量分裂型通量。一般前者相對于后者具有更小的耗散，但是前者更容易出現激波不穩定現象。通量差分型通量主要有Roe通量和Osher通量。Osher通量通過在相空間中將通量導數沿著積分曲線進行積分來提取左右迎風特性，它關于左右狀態是可微的，捕捉定激波非常銳利，而且一維情況下對應的Osher格式滿足熵條件[1-7]，但是在計算多維激波問題時原始的Osher通量容易出現激波不穩定。Amaladas和Kamath發現Osher通量計算強激波問題很難得到收斂解[8]。為了解決通量差分型通量的激波不穩定性問題，已有許多學者提出了各種修正方法。Sanders等基于5個界面的特征速度最大差異發展了一種H型的修正方法[9]。Pandolfi和D’Ambrosio基于相鄰4個界面的特征速度最大差異進行修正[10]，但是修正量的計算公式要比文獻[9]中的復雜。Ren提出了旋轉Riemann算子[11]。最近，筆者借鑒文獻[9-10]的思想，給出了一種基于相鄰界面的局部最大特征速度變化量的簡化熵修正方法，測試結果表明修正的Osher通量改善了一階格式和二階格式的多維激波問題求解的魯棒性[12]。本文將該修正的Osher通量運用到高階精度格式的計算中。

高階加權緊致非線性格式(WCNS)是鄧小剛和毛枚良在1997年提出的[13]，WCNS對物理變量作非線性加權插值，在光滑區域各子模板的權值趨于最優權使得格式達到五階精度，在間斷附近跨間斷模板取近似零權值以阻止跨間斷插值。2011年他們又提出了混合使用節點和半節點的混合型WCNS(HWCNS)[14]，同年還提出了守恒網格導數計算方法(CMM)使得格式滿足幾何守恒律[15]。由于CMM形式不唯一，2013年鄧小剛等又提出了SCMM網格導數計算方法[16]，解決了網格導數和雅可比計算的唯一性問題。大量的數值模擬表明滿足幾何守恒律的WCNS具有很強的網格適應性和魯棒性[17-19]。通量的設計對于高階激波捕捉格式是非常重要的。目前，WCNS大都采用Steger-Warming通量和Roe通量，還沒有運用Osher通量以及與其他通量進行比較。

本文將修正的Osher通量運用于高階WCNS，并對格式特性進行研究。通過二維無黏和黏性圓柱繞流、層流邊界層、激波邊界層干擾、空心圓柱裙(Hollow Cylinder-Flare)和三維鈍錐高超聲速繞流算例的模擬，測試了該計算策略的激波穩定性、熱流預測精度和邊界層模擬能力。

1 控制方程和高階WCNS

三維可壓非線性Navier-Stokes方程可寫為

式中：U為守恒向量，下標t表示時間；Fi和Fv分別為無黏通量和黏性通量。取黏性通量為零，則Navier-Stokes方程退化為Euler方程，其形式及其在曲線坐標系下的變換形式詳見文獻[16]。本文將主要基于二維Euler方程介紹Osher通量和修正方法，該修正方法在三維的推廣是直接而簡單的。二維Euler方程的形式為

Ut+f(U)x+g(U)y=0

(1)

(2)

式中：f、g分別為x、y方向的通量函數；ρ為密度；u、v分別為x、y方向的速度分量；e為總能；p為壓力；狀態方程為p=(γ-1)·(e-ρ(u2+v2)/2)；γ為比熱比。

由物理空間到計算空間的坐標變換為ξ=ξ(x,y)，η=η(x,y)，τ=t，其中ξ、η與τ分別為計算空間中的2個空間坐標和時間坐標。此時式(1)變為

(3)

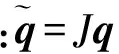
高階WCNS的空間離散包括3個方面內容：計算通量導數的差分格式、計算半點左右值的插值算法和計算半點通量的計算格式。本文考慮五階WCNS，通量導數的差分算子采用六階差分算子，

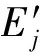
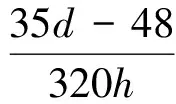
(4)

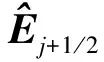
本文著重討論的是半點通量的計算格式，筆者將考慮原始的Osher通量、修正的Osher通量以及作為對比的Roe通量和Steger-Warming通量。時間離散采用三步Runge-Kutta方法[21]。對于Navier-Stokes方程的黏性項中導數的離散，本文采用六階中心差分格式。

2 Osher通量和修正方法

2.1 Osher通量

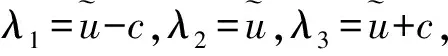
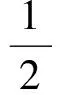
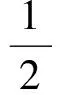
(5)

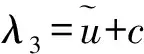
2.2 修正方法

由于原始的Osher通量在處理多維問題時仍然按一維Riemann問題近似地計算單元邊界面的數值通量，在計算多維激波時容易出現紅斑現象或者激波不穩定現象。文獻[12]針對一階精度和二階精度的有限體積方法，借鑒文獻[9-10]的思想，基于垂直于控制體交界面的4個界面兩側的特征速度信息對Osher通量進行修正，數值結果表明該修正可以改善Osher通量在多維激波模擬時的魯棒性。本文將修正方法推廣應用于高階WCNS中，對半點處的Osher通量進行修正。

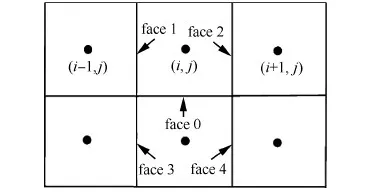
圖1 與界面face 0相接的4個界面 Fig.1 Four interfaces connected to interface face 0

考慮圖1中face 0上半點處的通量，基于垂直方向的局部最大特征速度變化量引入修正量，得到修正的Osher通量為

(6)

對于三維情況，該修正方法的推廣是直接的，只是垂直于交界面的相鄰界面變為8個。

3 數值結果與分析

本節將運用圓柱繞流、激波邊界層干擾、空心圓柱裙等算例，測試基于修正Osher通量的WCNS的激波穩定性、熱流計算精度和邊界層模擬能力。

3.1 無黏圓柱繞流

考慮無黏圓柱繞流，計算狀態為Ma∞=8.0。研究結果表明網格與激波的相對位置對通量的激波穩定性有較為明顯的影響，相對位置的微弱變化可能導致激波穩定性結果完全不同[22]。本文通過微弱地改變網格與激波相對位置生成了11套網格來測試激波穩定性，網格生成方法詳見文獻[12]。對于激波的穩定性，有對稱性、收斂性、激波位置3個方面的考察指標，如表1所示。這樣對數值解作質量評估分為8種，如表2所示，其中數值解特性中3個數字依次分別代表對稱性、收斂性和激波位置指標，例如類型5表示對稱的不收斂的激波位置正確的解。

為了書寫方便，將本文修正的Osher通量，簡記為Osher-Z，將基于Harten熵修正[23]的Roe通量記為Roe-Harten，將基于本文修正的Roe通量記為Roe-Z。表3給出了各種通量的測試結果。在所有11套網格中Osher-Z和Steger-Warming通量都能得到對稱、收斂、正確的解，都沒有出現“紅斑”現象。Roe-Harten在其中的7套網格上會出現紅斑或者激波不穩定現象，而Roe-Z通量不會出現嚴重的紅斑現象，但還是會在其中的 5套網格上出現激波不穩定、流場不對稱的現象。以上結果表明，Osher-Z通量在捕捉激波的魯棒性方面與Steger-Warming通量是相近的，并且明顯優于Roe通量。

表1 數值解的3種特性Table 1 Three properties of numerical solution

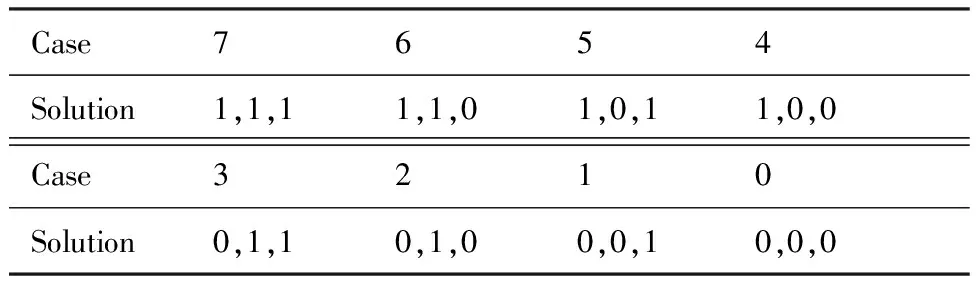
表2 數值解的質量評估Table 2 Quality evaluation of numerical solution

表3不同激波網格相對位置下不同通量的測試結果

Table3Testresultsfordifferentnumericalfluxesongridswithdifferentshock-grid-position

Flux012345678910Osher00000000000Osher?Z77777777777Roe?Harten77000000577Roe?Z44444777777Steger?Warming77777777777

3.2 黏性圓柱繞流

高超聲速二維黏性圓柱繞流的熱流預測問題是測試通量捕捉激波穩定性和測試通量熱流預測能力的一個良好算例，許多研究工作都基于該算例對通量進行考核[22，24]。其計算條件為來流馬赫數Ma∞=8.1，來流壓力P∞=370.6 Pa，雷諾數Re=1.3×105，來流溫度T∞=63.73 K，壁溫Tw=300 K。所采用的網格頭部局部圖如圖2(a)所示。在本算例中Roe-Harten會出現紅斑現象，不能得到正確的激波解，如圖2(b)所示，因此不再對其進行考核。

通過改變壁面第1層網格雷諾數測試各通量的熱流計算精度和網格適應性，本文考慮3套網格，第1層網格雷諾數分別為13、53和208。圖3給出了這3套網格上基于不同通量的五階WCNS計算得到的壁面熱流分布圖，其中：θ為圓柱表面對應點至圓心的連線與x軸之間的夾角；q為物面熱流；q0為圖柱頭部熱流。可以看出Roe-Z流，得到的熱流值相近，隨壁面第1層網格的網格雷諾數變化并不大。相反地，Steger-Warming通量的熱流值隨第1層網格雷諾數的變化較大，當網格雷諾數為52時，頭部熱流已經出現偏差，而當網格雷諾數達到208時，頭部已出現非常明顯的過熱，熱流值偏離理論值較遠。

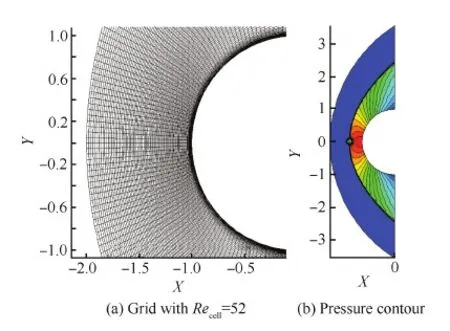
圖2 計算網格和Roe-Harten通量計算得到的壓力圖 Fig.2 Computational grid and pressure contour obtained by Roe-Harten flux

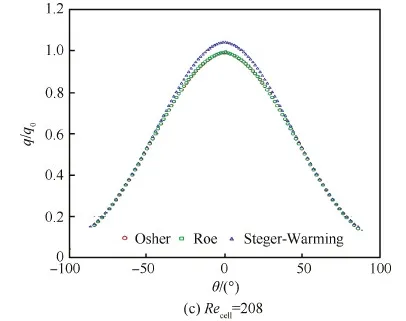
圖3 不同雷諾數時第1層網格的壁面熱流分布 Fig.3 Surface heating profiles of different fluxes for different grid Reynolds number

3.3 平板邊界層算例

考慮低速平板邊界層的流動，計算狀態為Ma∞=0.2,Re=2.0×106。計算域為一長方形，入口邊界位于平板頭部前1/2平板長度處，上邊界位于1/2倍平板長度處。考慮兩套計算網格：第1套網格規模為104×96(流向×法向)并且物面網格雷諾數為Recell=5，第2套網格50×62(流向×法向)并且Recell=100，如圖4所示。

截取x=1線上的速度分布并與Blasius解進行比較。圖5和圖6分別給出了Recell=5和Recell=100情況下分別運用修正的Osher通量、基于Harten修正的Roe通量和Steger-Warming通量的WCNS計算結果，圖中η為無量綱坐標。

從圖5和圖6中可看出，對于x方向速度u，當Recell=5時Osher通量和Roe通量的結果相近，而Steger-Warming通量計算結果有微弱的偏離；當Recell=100時Osher通量的結果仍然與Blasius解符合得很好，Roe通量結果出現微弱偏離，而Steger-Warming的結果出現明顯的偏離，最大偏離處達到10%。對于y方向速度v，當Recell=5時Osher通量比Roe通量的結果更靠近Blasius解，而Steger-Warming的結果出現較大偏離；當網格雷諾數為100時，Roe通量計算結果也偏離Blasius解，Steger-Warming的結果偏離變得更大，最大偏離處達到20%。

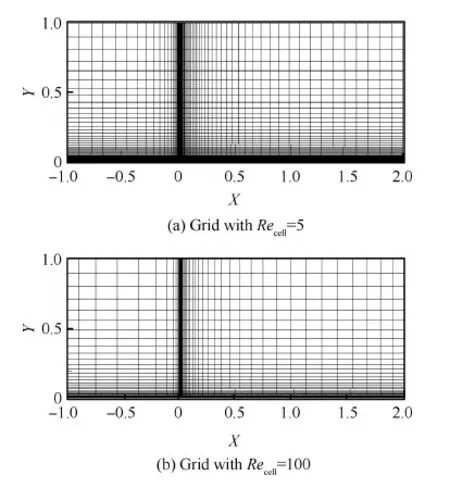
圖4 平板邊界層的2套計算網格 Fig.4 Two grids for boundary layer computing

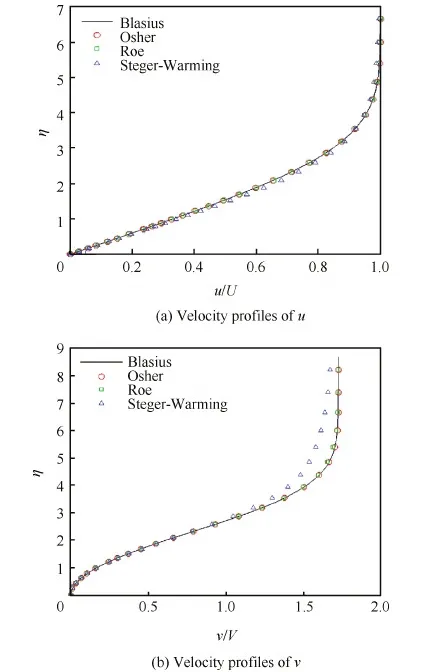
圖5 x=1處的速度分布(Recell=5) Fig.5 Velocity profiles for x=1 (Recell=5)

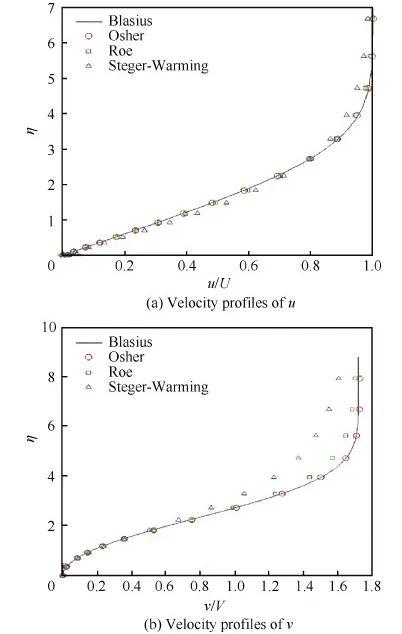
圖6 x=1處的速度分布(Recell=100) Fig.6 Velocity profiles for x=1 (Recell=100)

從上述結果可以看出，相比Roe通量和Steger-Warming通量，Osher通量的數值耗散小，能夠更好地模擬出層流邊界層附近的黏性流動，Osher通量的結果隨第1層網格雷諾數的變化更小，模擬邊界層更加準確，能在較大的網格雷諾數下得到較為準確的邊界層，從而能夠降低格式對網格量的需求。

3.4 激波平板邊界層干擾

入射斜激波和層流平板邊界層干擾算例是最簡單的激波邊界層干擾算例，通過該算例可以很好地考察計算方法對這類問題的模擬能力。在該問題中，從x=0開始有1個平板，1個入射角度為30.8° 的斜激波在xsh=1處與平板邊界層相互干擾，來流狀態為Ma∞=2.15，Re=2.0×106，其中雷諾數的參考長度為xsh。具體計算狀態和邊界處理可以參見文獻[25]。

采用修正的Osher通量、Steger-Warming通量和基于Harten修正的Roe通量3種通量對該問題進行了計算。圖7中給出了Osher通量計算得到的無量綱壓力云圖。在激波入射點(xsh)附近，邊界層會產生小尺度的流動分離，要準確地模擬這些流動現象不僅要魯棒地模擬激波以及激波/激波干擾，而且還需要準確的模擬平板邊界層的發展。圖8給出了不同通量的計算結果沿物面的壓力分布，并與實驗結果進行了對比。從圖中可看出，Osher通量的計算結果與實驗結果符合得較好；在本算例中，Roe通量計算結果在大部分區域都與Osher計算結果相近，兩者未展現出明顯差異；然而，Steger-Warming通量的計算結果與實驗結果出現了明顯的偏差。

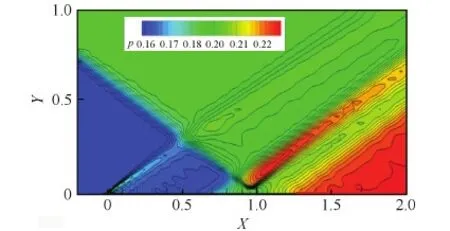
圖7 無量綱壓力云圖 Fig.7 Nondimensional pressure contour

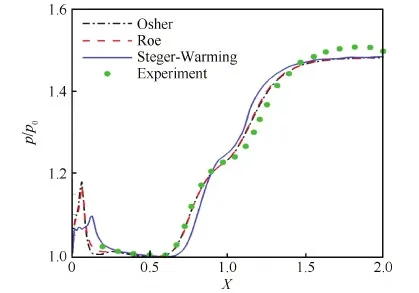
圖8 不同通量物面壓力分布圖 Fig.8 Wall pressure distributions for different fluxes

3.5 空心圓柱裙

空心圓柱裙算例包含復雜的壓縮拐角流動和激波邊界層干擾現象[26-27]，通過該算例可以很好地測試不同求解方法對這類問題的模擬能力。其模型外形及尺寸如圖9所示，對稱面上的計算網格如圖10所示。通過改變物面法向網格數目生成了一系列網格(法向網格數分別為40、60和100)，通過不同網格密度的模擬結果來測試不同通量對這類問題的模擬能力。

圖9 空心圓柱裙算例模型尺寸 Fig.9 Size of hollow cylinder-flare model

計算采用了之前算例中耗散較小的修正的Osher通量和基于Harten修正的Roe通量。圖11 給出了相應的計算結果，其中法向網格數為100的2個模擬結果幾乎完全重合，此處僅僅給出了其中Osher通量的模擬結果。無論是壓力系數Cp還是熱流Q分布，隨著網格的加密兩者都會逐漸趨近于網格收斂解，而且網格收斂解在大部分區域能夠與實驗結果較好地吻合。Osher通量和Roe通量的計算結果僅僅在最粗的網格上表現出較明顯的差異，在其他網格上兩者計算結果差異較小。

圖10 空心圓柱裙算例對稱面計算網格 Fig.10 Grids of symmetric face of hollow cylinder-flare

圖11 空心圓柱裙算例壓力系數和熱流分布 Fig.11 Pressure coefficients and heat flux profiles of hollow cylinder-flare

3.6 三維鈍錐高超聲速繞流

采用鈍錐高超聲速繞流[17]測試Osher通量在高超聲速三維黏性流動中的表現。鈍錐球頭半徑為Rn=27.94 mm，半錐角為15°，長度為球頭半徑的16倍。計算條件：來流馬赫數Ma∞=10.6，迎角α=20°，每米雷諾數Re=3.973×106m-1，來流溫度T∞=47.3 K，壁溫Tw=294.44 K。

所采用的計算網格，物面網格雷諾數Recell=Re·Δn≈4,其中Δn為物面附近第1層網格垂直物面方向的網格尺寸。圖12給出了修正的Osher通量的計算結果在不同子午面上的熱流分布(用駐點熱流值Qw0歸一化)，并與實驗結果進行了對比。從計算結果來看，Osher通量計算結果與實驗結果吻合較好。

高超聲速流動中熱流的預測結果對計算網格非常敏感，邊界層內通常需要很密的計算網格來保證熱流計算結果的正確性。發展網格敏感性低、在較稀網格下能夠正確預測熱流分布的計算方法對熱流的工程預測有重要意義。本文在圖12 的密網格(Fine Grid)的基礎上生成了一系列較稀的網格，對不同通量的網格敏感性以及在較稀網格中的熱流預測能力進行測試。圖13給出了θ=90° 子午面上不同通量在不同網格上計算結果的對比。其中基于Harten修正的Roe通量僅僅在最稀網格上得到了物理的解，而在最密網格和中等網格上都出現了激波不穩定現象，無法給出物理的解。圖14給出了密網格上修正的Osher通量和基于Harten修正的Roe通量的熱流云圖。Osher通量在3套網格中均未出現激波不穩定現象，其魯棒性明顯優于Roe通量。在未出現激波不穩定的計算結果中，Osher通量明顯給出了最接近網格收斂解的計算結果，即使在最稀的網格上計算結果依然比較準確。

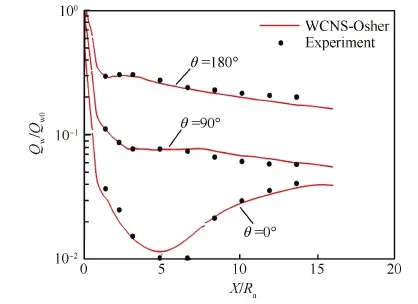
圖12 鈍錐算例熱流計算結果 Fig.12 Heat flux computational results of blunt cone

圖13 鈍錐算例不同網格下不同通量的熱流對比 Fig.13 Comparison of heat flux computational results of blunt cone for different fluxes on different grids

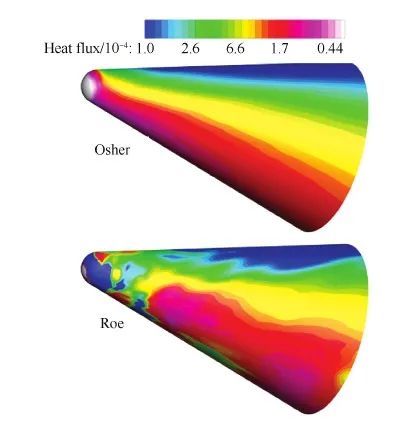
圖14 鈍錐算例無量綱熱流云圖 Fig.14 Dimensionless heat flux contour on blunt cone

圖13中同時給出了采用文獻[28]中總變差不增(Total Variation Diminishing, TVD)限制的三階精度格式在中等網格上的計算結果。類似WCNS的測試結果，采用Roe通量的計算結果出現了嚴重的激波不穩定，而Osher通量的計算結果未出現激波不穩定，說明了Osher通量比Roe通量更魯棒，而且Osher通量的熱流計算結果明顯優于Steger-Warming通量的計算結果。

該算例結果表明，3種通量的特性在三維算例中的結論與在二維算例上的結論保持一致。

4 結 論

本文研究了一種修正的Osher通量在高階WCNS中的特性，并與Roe通量和Steger-Warming通量進行對比。二維高超聲速無黏和黏性圓柱繞流算例、層流邊界層算例、激波邊界層干擾算例、空心圓柱裙(Hollow Cylinder-Flare)算例和三維鈍錐高超聲速繞流的計算結果表明：

1) 修正的Osher通量的激波穩定性比Roe通量好，與Steger-Warming相近。

2) 修正的Osher通量在光滑區域相對Steger-Warming通量具有更小的耗散，耗散與Roe通量耗散接近，能夠在較稀的網格上更好地模擬邊界層和熱流分布。

上述結果說明了Osher通量在高階格式中的特性優于Roe通量和Steger-Warming通量。

[1] ENGQUIST B, OSHER S. Stable and entropy satisfying approximations for transonic flow calculations[J]. Mathematics of Computation, 1980, 34(149): 45-57.

[2] ENGQUIST B, OSHER S. One sided difference approximation for nonlinear conservation laws[J]. Mathematics of Computation, 1981, 36(154): 321-351.

[3] OSHER S, SOLOMON F. Upwind difference schemes for hyperbolic systems of conservation laws[J]. Mathematics of Computation, 1982, 38(158): 339-374.

[4] OSHER S, CHAKRAVARTHY S. Upwind schemes and boundary conditions with application to Euler equations in general geometries[J]. Journal of Computational Physics, 1983, 50(3): 447-481.

[5] CHAKRAVARTHY S, OSHER S. Numerical experiments with the Osher upwind scheme for the Euler equations[J]. AIAA Journal, 1983, 21(9): 1241-1248.

[6] OSHER S. Riemann solvers, the entropy condition, and difference approximations[J]. SIAM Journal on Numerical Analysis, 1984, 21(2): 217-235.

[7] OSHER S, CHAKRAVARTHY S. High resolution schemes and the entropy condition[J]. SIAM Journal on Numerical Analysis, 1984, 21(5): 955-984.

[8] AMALADAS J R, KAMATH H. Accuracy assessment of upwind algorithms for steady-state computations[J]. Computers & Fluids, 1998, 27(8): 941-962.

[9] SANDERS R, MORANO E, DRUGUET M. Multidimensional dissipation for upwind schemes: Stability and applications to gas dynamics[J]. Journal of Computational Physics, 1998, 145(2): 511-537.

[10] PANDOLFI M, D’AMBROSIO D. Numerical instabilities in upwind methods: Analysis and cures for the “carbuncle” phenomenon[J]. Journal of Computational Physics, 2001, 166(2): 271-301.

[11] REN Y X. A robust shock-capturing scheme based on rotated Riemann solvers[J]. Computers & Fluids, 2003, 32(10): 1379-1403.

[12] ZHU H J, DENG X G, MAO M L, et al. Osher flux with entropy fix for two-dimensional Euler equations[J]. The Advances in Applied Mathematics and Mechanics, 2016， 8(4): 670-692.

[13] DENG X G, MAO M L. Weighted compact high-order nonlinear schemes for the Euler equations: AIAA-1997-1941[R]. Reston: AIAA, 1997.

[14] DENG X G, MAO M L. New high-order hybrid cell-edge and cell-node weighted compact nonlinear schemes: AIAA-2011-3857[R]. Reston: AIAA, 2011.

[15] DENG X G, MAO M L, TU G H, et al. Geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2011, 230(4): 1100-1115.

[16] DENG X G, MIN Y B, MAO M L, et al. Further studies on geometric conservation law and applications to high-order finite difference schemes with stationary grids[J]. Journal of Computational Physics, 2013, 239: 90-111.

[17] 燕振國, 劉化勇, 毛枚良, 等. 三階HWCNS的構造及其在高超聲速流動中的應用[J]. 航空學報, 2015, 36(5):1460-1470.

YAN Z G, LIU H Y, MAO M L, et al. Development of 3rd-order HWCNS and its application in hypersonic flow[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1460-1470 (in Chinese).

[18] 涂國華, 燕振國, 趙曉慧, 等. SA和SST湍流模型對高超聲速邊界層強制轉捩的適應性[J]. 航空學報, 2015, 36(5):1471-1479.

TU G H, YAN Z G, ZHAO X H, et al. SA and SST turbulence models for hypersonic forced boundary layer transition[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(5): 1471-1479 (in Chinese).

[19] 燕振國, 劉化勇, 毛枚良, 等. 基于高階耗散緊致格式的GMRES方法收斂特性研究[J]. 航空學報, 2014, 35(5): 1181-1192.

YAN Z G, LIU H Y, MAO M L, et al. Convergence property investigation of GMRES method based on high-order dissipative compact scheme[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(5): 1181-1192 (in Chinese).

[20] DENG X G, ZHANG H X. Developing high-order weighted compact nonlinear schemes[J]. Journal of Computational Physics, 2000, 165(1): 22-44.

[21] SHU C W, OSHER S. Efficient implementation of essentially non-oscillatory shock capturing schemes[J]. Journal of Computational Physics, 1988, 77(2): 439-471.

[22] KITAMURA K, SHIMA E, NAKAMURA Y, et al. Evaluation of Euler fluxes for hypersonic heating computations[J]. AIAA Journal, 2010, 48(4): 763-776.

[23] HARTEN A. On a class of high resolution total-variation-stable finite-difference schemes[J]. SIAM Journal of Numerical Analysis, 1984, 21(1): 1-23.

[24] KITAMURA K. A further survey of shock capturing methods on hypersonic heating issues: AIAA-2013-2698[R]. Reston: AIAA, 2013.

[25] MA Y K, YAN Z G, ZHU H J. Improvement of multistep WENO scheme and its extension to higher orders of accuracy[J]. International Journal of Numerical Methods Fluids, 2016, 82(12): 818-838.

[26] DELERY J M， PANARAS A G. Shock-wave/boundary-layer interactions in high-Mach-number flows: AGARD-AR-319[R]. 1996.

[27] MOSS J N， DOGRA V K， PRICE J M. DSMC simulations of viscous interactions for a hollow cylinder-flare configuration: AIAA-1994-2015[R]. Reston: AIAA, 1994.

[28] KIM K H, KIM C. Accurate, efficient and monotonic numerical methods for multi-dimensional compressible flows Part II: Multi-dimensional limiting process[J]. Journal of Computational Physics, 2005, 208(2): 570-615.

(責任編輯： 鮑亞平, 蔡斐)

URL：www.cnki.net/kcms/detail/11.1929.V.20160926.0950.006.html

PropertiesofOsherfluxwithentropyfixinhigh-orderWCNS

ZHUHuajun1,YANZhenguo1,LIUHuayong1,*,MAOMeiliang1,2

1.StateKeyLaboratoryofAerodynamics,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China2.ChinaComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China

Osherfluxwithamulti-dimensionalentropyfixisappliedforhighorderweightedcompactnonlinearscheme(WCNS).Theentropyfixtechniqueisusedtomainlyimprovethedissipationontheinterfacesperpendiculartotheshockwave,andcanthusimproveshockwavestabilityandmaynotinfluencecontactresolution.ThepropertiesoftheOsherfluxinhighorderWCNSschemesarestudied.Numericalinvestigationsaremadetotestpropertiesofshockwavestability,accuracyofviscousheatingcomputation,andboundarylayerandshockboundarylayerinteractioncalculationabilities.ComparisonswithSteger-WarmingfluxandRoefluxarealsomade.NumericalresultsshowthattheOsherfluxwithentropyfixismorerobustthanRoefluxwithHartenfixinshockcapturing,andisbetterinviscousheatingcomputationthanSteger-Warmingflux.TheseresultsillustratethathighorderWCNSbasedonOsherfluxwithentropyfixisrobustincaputuringshockwaves,cangetaccurateheatflowpredictionandhasgoodsimulationoftheboundarylayer.

flux;highorderWCNS;shockwavestability;heatflowcomputation;boundarylayercalculation

2016-06-17；Revised2016-07-28；Accepted2016-08-25；Publishedonline2016-09-260950

s：NationalNaturalScienceFoundationofChina(11301525,11372342and11572342)

.E-mailhyliu@skla.cardc.cn

2016-06-17；退修日期2016-07-28；錄用日期2016-08-25； < class="emphasis_bold">網絡出版時間

時間：2016-09-260950

www.cnki.net/kcms/detail/11.1929.V.20160926.0950.006.html

國家自然科學基金 (11301525,11372342,11572342)

.E-mailhyliu@skla.cardc.cn

朱華君， 燕振國， 劉化勇， 等． 一種修正的Osher通量在高階WCNS中的特性J． 航空學報,2017,38(5):120543.ZHUHJ,YANZG,LIUHY,etal.PropertiesofOsherfluxwithentropyfixinhigh-orderWCNSJ.ActaAeronauticaetAstronauticaSinica,2017,38(5):120543.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0241

V211; O355

A

1000-6893(2017)05-120543-10