尋找數學有趣的密碼

文︳徐 晟

尋找數學有趣的密碼

文︳徐 晟

很多人都說數學是枯燥的，乏味的學科。這是因為數學是形式科學的一種，它抽象、嚴密，越到高一級知識越明顯，學生不易接受。所以，教學時一定要將數學知識通俗化、趣味化，才能讓學生易于理解。但現實教學情況不容樂觀，因此許多學生學數學時感到恐懼和焦慮。

比如，中學數學中“無理數”概念的學習。這個概念可是引發了數學史上的第一次數學危機，它是抽象的、難理解的。如果教學中不作通俗化的處理，學生根本就不知道這個概念是怎么產生的，有什么本質屬性。因此，教材是這樣編排的（如圖）。

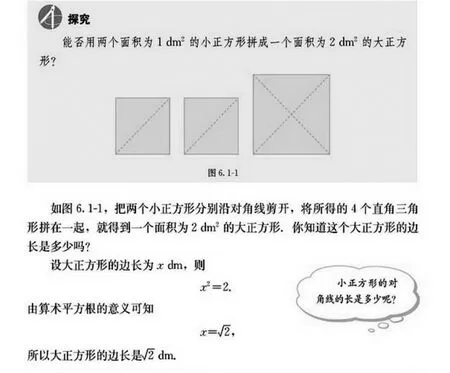
為什么學習數，要從幾何開始？這樣設計，是符合歷史，也符合邏輯的。因為，無理數的發現，正是從研究正方形的對角線與邊的關系中產生的。

歷史上，古希臘數學家畢達哥拉斯將數學知識運用得純熟之后，覺得不能只滿足于用來算題解題，于是他試著從數學領域擴大到哲學，用數的觀點去解釋世界。經過一番刻苦實踐，他提出“萬物皆為數（指有理數）”的觀點：數的元素就是萬物的元素，世界是由數組成的，世界上的一切沒有不可以用數來表示的，數本身就是世界的秩序。

但是，畢達哥拉斯學派的弟子希帕索斯發現了一個驚人的事實，一個正方形的對角線與其一邊的長度是不可公度的（若正方形的邊長為1，則對角線的長不是一個有理數）。這一不可公度性與畢氏學派的“萬物皆為數”的觀點大相徑庭。這一發現使該學派領導人惶恐，認為這將動搖他們在學術界的統治地位，于是極力封鎖該真理的流傳。希帕索斯被迫流亡他鄉。不幸的是，在一條海船上還是遇到畢氏門徒。最終他被畢氏門徒殘忍地投入了水中殺害。

希帕索斯的發現，第一次向人們揭示了有理數系的缺陷，證明了它不能同連續的無限直線等同看待，有理數并沒有布滿數軸上的點，在數軸上存在著不能用有理數表示的“孔隙”。而這種“孔隙”經后人證明簡直多得不可勝數。于是，古希臘人把有理數視為連續銜接的那種算術連續統的設想徹底地破滅了。不可公度的發現，對以后2000多年數學的發展產生了深遠的影響，促使人們從依靠直覺、經驗轉向依靠證明，推動了公理幾何學和邏輯學的發展，并且孕育了微積分思想。人們為了紀念希帕索斯這位為真理而獻身的可敬學者，就把不可公度的量取名“無理數”——這就是無理數的由來。

由無理數引發的數學危機一直延續到19世紀下半葉。1872年，德國數學家戴德金從連續性的要求出發，用有理數的分割來定義無理數，并把實數理論建立在嚴格的科學基礎上，從而結束了無理數被認為無理的時代，也結束了持續2000多年的數學史上的第一次大危機。

由此看來，無理數來之不易，學習無理數概念時，讓學生知道這段歷史，既可以幫助他們更好地理解概念，也增添了趣味性。

你是有心人，教學可以從這一點出發，學習概念后，再讓學生從數學美的角度體驗數學的有趣。

我們來看看與無理數有關的美妙的式子，趣味會來得更足。比如這個式子：

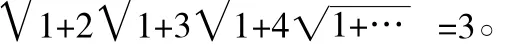
這個優美的式子來自印度數學奇才拉馬努金。他曾經深入地研究了形如上式的無窮根式并得到了這個神奇的結果。傳說拉馬努金曾經把這個結果放在《印度數學會刊》上征集證明，結果數月內無人能應。

如果上式還不足以讓人驚嘆，那再看看這個：

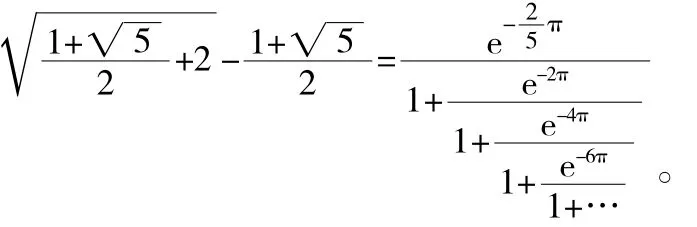
這個絕美的公式不僅將圓周率和e聯系起來，還將黃金分割數也包含在內。它的發現者，仍然是印度數學奇才拉馬努金。1913年，來自南印度的小職員拉馬努金，給當時32歲就已經執掌英國數學界牛耳的哈代去了一封長達9頁的信，信中附帶了120條他發現的公式，上面這個公式就是其中的一條。這條公式令哈代完全摸不著頭腦，他從沒見過這樣的公式，連稍微接近點的都沒有！但是哈代確信這個公式是對的，因為沒有人能有這樣的想象力去編造這樣漂亮的公式。果然不久之后，數學家們就嚴格地證明了這個公式，它和諧而又氣勢磅礴的形式令每一個初次見到它的人都會為之悸動！借用哈代的一句話：“這個公式完全打敗了我，我無法確信世界上居然還會有這種東西存在！”

數學就是那么巧妙，圓周率和e都是無理數，那你再看看它——eπi+1=0。這就是受到我們萬世敬仰的歐拉公式。它將數學里最重要的幾個數字聯系到了一起：兩個無理數：自然對數的底e，圓周率π；兩個單位：虛數單位i和自然數的單位1；以及被稱為人類偉大發現之一的0。數學家們評價它是“上帝創造的公式”。

歷史上的歐拉是一位全才數學家，同時也是一名虔誠的教徒，篤信上帝的存在。據說有一次俄國的葉卡捷琳娜二世邀請狄德羅訪問她的宮廷，而狄德羅是一名不折不扣的無神論者。不久，葉卡捷琳娜二世就厭倦了狄德羅那喋喋不休的無神論說教之詞，讓歐拉來好好教訓他一頓。歐拉開門見山地質問道：“eπi+1=0，所以上帝存在，請回答！”結果不懂數學的狄德羅被弄得一頭霧水，無言以對。

你看，本來枯燥難懂的無理數概念，經過挖掘，前后多了許多有趣的事情。學習前，可以了解歷史故事，學習后，可以欣賞美妙的公式。

也許你會問，欣賞過后呢？我們能否自己創造？最后看看這個例子，你就知道答案了。

話說世人皆知勾三股四弦五，而鮮有人知道這個簡單的等式：33+43+53=63。這個完美的式子可以在上述提到的英國數學家哈代所著的《數論導引》中找到，它是一類三次不定方程最簡單的特解。學習勾股定理時，我們都會寫32+42=52。然而寫完就了事。實際上，稍微類比運算一下，就能得出33+43+53=63。可是，大家都沒有想到它，與數學有趣的密碼失之交臂，多么令人遺憾！

（作者單位：長沙市雅禮中學）