數學實驗課堂需要“生動”

吳永慶

[摘 要]數學實驗課堂是開放性的課堂，它能夠給予學生積極思考、動手實踐、自主探索、合作交流的機會，是學生經歷知識的形成過程，感悟數學思想和方法，獲得基本的數學活動經驗的重要場所。在數學實驗課堂中應該給予學生充足的實驗探究時間，盡可能不給或少給限制和提示，鼓勵學生用自己喜歡的契合自身實際的認知方式去探索和發現，尊重學生思維的獨立性和多樣性。

[關鍵詞]多邊形內角和；實驗；生動

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2017）29-0028-02

弗賴登塔爾提出：“‘學一個活動的最好方法是做，通過‘做進行‘再創造。”《義務教育數學課程標準（2011年版）》也提出：“學生學習應當是一個生動活潑的、主動的和富有個性的過程。認真聽講、積極思考、動手實踐、自主探索、合作交流等，都是學習數學的重要方式。學生應當有足夠的時間和空間經歷觀察、實驗、猜測、計算、推理、驗證等活動過程。”因此，教師在課堂中要挖掘可以給學生進行實驗活動的素材，創設實驗問題情境，由學生主動構建解決問題的基礎模型，給予學生充足的實驗探究時間，讓學生多角度嘗試和發現，從而經歷知識的形成過程，感悟數學思想和方法，獲得基本的數學活動經驗，最終形成數學研究素養。

【教學片段一】自主探究 尋求方向

（從四邊形開始探索多邊形的內角和時，學生通常會選擇一些特殊的四邊形，試圖通過特殊的例子尋找實驗的思路和方法）

生1：我們組選用正方形來研究。正方形的四個角都是90°，所以四邊形的內角和是360°。

生2：我們組選用長方形進行研究。由于長方形的四個角都是90°，所以我們認為四邊形的內角和是360°。

生3：我們組選擇的是平行四邊形。把平行四邊形分成兩個三角形，一個三角形的內角和是180°，平行四邊形的內角和就是兩個180°，也就是360°，所以我們也認為四邊形的內角和是360°。

（雖然學生選擇的都是特殊的多邊形，但他們的實驗思路卻具有一般性）

師：其他的四邊形的內角和也可以像平行四邊形一樣分成兩個三角形來求嗎？請小組合作，任意畫一個四邊形進行實驗研究。

生（實驗研究后總結）：不論是什么樣的四邊形，只要任意連接其中一條對角線，就可以把四邊形分成兩個三角形（如圖1）。因此，四邊形的內角和是360°。

實驗研究能夠培養學生的思維能力、動手能力、探索和合作精神，因此，教師應設計開放式的實驗，在學生實驗探究過程中盡可能不給或少給限制和提示，讓學生自主尋找實驗思路，思考實驗方法。對于同一問題，學生在探究時會出現殊途同歸的情況，對此，教師應當在學生實驗探究的過程中扮演問題關鍵點的點撥者，引導學生把握實驗研究的方向。在四邊形內角和的研究中，其中兩組學生通過研究正方形和長方形很快就猜測四邊形的內角和是360°，這是試圖從特殊情況去獲取一般情況，而第三組的學生把平行四邊形轉化成兩個三角形，通過三角形的內角和推理得到四邊形的內角和。雖然平行四邊形也是特殊的四邊形，但這個實驗的思路和方法卻是值得推廣的。此時，教師應通過追問引導學生步入正確的實驗軌道。顯然，只有在教學中給予學生廣闊的實驗空間，對學生思維不加限制，并在學生遇到困難時進行點撥，才能讓學生充分地動起來。

【教學片段二】方法遷移 多面開花

（對于五邊形的內角和，因為已經有了四邊形內角和的研究經驗，絕大多數學生很容易想到將五邊形分成若干個已知內角和的多邊形來進行研究）

生1：我們把五邊形分成三個三角形（如圖2），所以五邊形的內角和是180°×3=540°。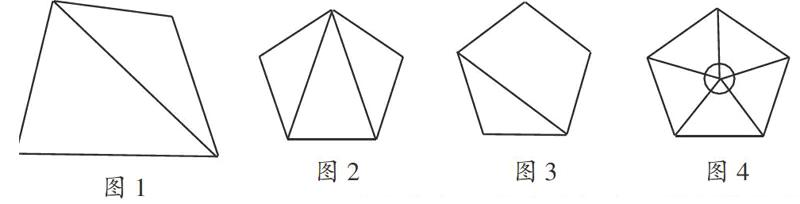

生2：我們把五邊形分成一個三角形和一個四邊形（如圖3），所以五邊形的內角和是180°+360°=540°。

生3：我們把五邊形分成五個三角形（如圖4），但是中間卻多算了一個周角的度數，所以五邊形的內角和是180°×5-360°=540°。

對于五邊形內角和的實驗探究，教材推薦的方法與生1的相同，從節省時間的角度來講，教師可以直接引導學生利用生2的方法進行研究，然而，積累數學實驗經驗重于知識的獲取，只有在探究時給予學生充足的時間，不束縛研究思路，回報才會是豐碩的：學生的思路打開了，他們能夠利用探索四邊形內角和的經驗，將五邊形轉化成已知內角和的多邊形，這不僅僅是三角形，也可以是三角形“+”四邊形；不僅僅是“+”，也可以出現“-”——生3的思路又為深度探究提供了思維支撐。至此，學生的“動”讓整節課展現了更新的活力。

【教學片段三】提煉規律 深度理解

1.成果匯總，初探規律

根據推導出的不同多邊形的內角和，教師組織學生歸納并總結規律。

2.深度探究規律

師：多邊形的內角和為什么不是幾條邊就是幾個180°的和，而是邊數減2后乘以180°？你們能夠用自己的研究來解釋這個現象嗎？

生1：我們在研究五邊形內角和時將五邊形分成了五個三角形，但是這種分法必定多算了一個周角，也就是180°×2，所以用“180°乘以邊數（5）后必須減去多算的兩個180°。研究六邊形時也存在這樣的問題，所以多邊形的內角和一定是“180°×（邊數-2）”。

生2：我們是把多邊形分成若干個三角形，在分的時候發現至少三個頂點才能得一個三角形，在此基礎上，而每增加一個頂點，就會多得一個三角形，多邊形是幾條邊就有幾個頂點，那么這樣分得的三角形個數就必定比多邊形的頂點數少2，可以看成“邊數-2”，所以多邊形的內角和是“180×（邊數-2）”。endprint

弗賴登塔爾說：“在較低層次的活動過程中的想法、制造的數學工具等會變成高層次學習時思考的物件。”也就是說，在實驗探究的過程中，學生探究的思路，活動的過程、表達的語言、總結的公式等都會變成更高層次學習的媒介。對于這些重要的生成性資源，教師要有意識地進行拾取，讓學生退回下一層或自然進入更高層次的學習。在學生通過實驗探究出多邊形內角和的一般規律“180°×（邊數-2）”后，教師對學生的結論進行有意引導，可引發學生對規律的進一步探究，從而讓學生對于規律的理解上升到更高層次。

【教學片段四】外延拓展 擴大成果

師：其實多邊形除了內角之外還有外角。如圖5，這個三角形中的∠1、∠2、∠3是內角，而∠4、∠5、∠6是和這些內角相對應的外角。通過剛才的實驗探究我們發現每一種多邊形都有固定的內角和，且這些多邊形的內角和是有規律可循的，即180°的倍數，是不是多邊形的外角和和內角和一樣也存在著規律呢？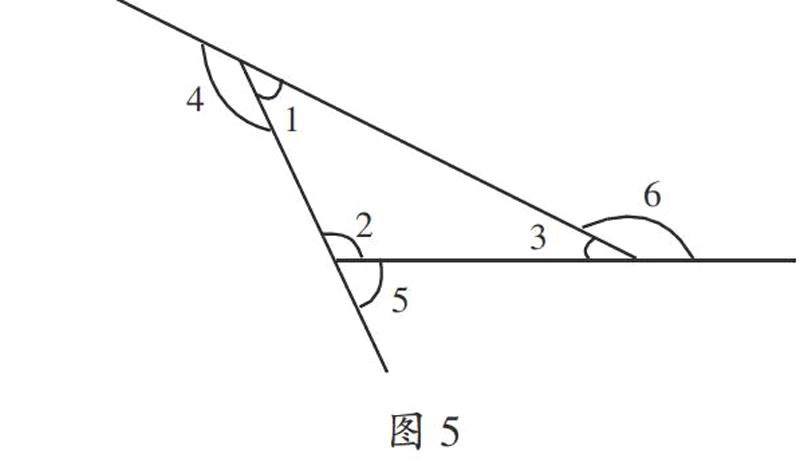

生1：我們組用量角器量出了每個外角的度數，求出三角形的外角和是360°。

生2：我們組是認為每個內角和對應的外角的和正好是一個平角（180°），那么三角形內角與外角的總和就是180°×3=540°，而三角形的內角和是180°，所以外角和就是540°-180°=360°。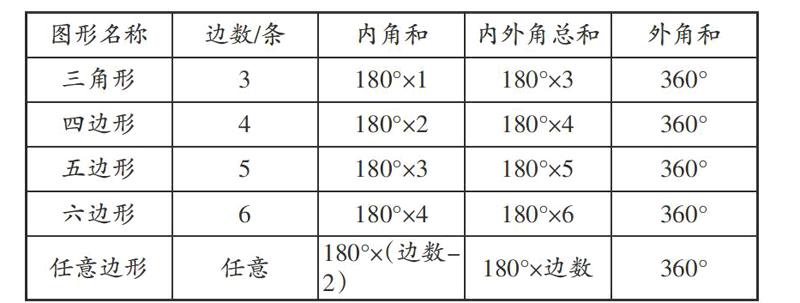

在研究三角形外角和的基礎上，學生自主實驗探究四邊形、五邊形、六邊形的外角和。

數學實驗課堂應當是開放性的課堂，教學內容的選擇不要拘泥于教材，要關注與學生探究活動中有關的知識，讓學生的體驗過程更加完整。通過數據匯總，學生發現內外角總和總是比內角和多“180°×2”，更是明晰了360°的來歷。這樣，外角和作為本節課的主要知識，既讓學生感受到了每種多邊形內角和的“統一”，又讓學生在教學最后對外角和的挖掘研究中感悟到數學的“同一”，這不正是數學的美嗎？

讓學生“動”起來的數學實驗課堂，能創造更多的機會并給予充足的時間讓學生在實驗探究中經歷知識形成的過程，從而理解數學概念、體會數學思想、形成數學技能。

[ 參 考 文 獻 ]

[1] 弗賴登塔爾.作為教育任務的數學[M].陳昌平，唐瑞芬等，編譯.上海：上海教育出版社，1995.

[2] 陳士文.白話數學：“1”和“三角形”[J].小學數學教師，2016（2）.

[3] 陳燕虹.“數學是人類活動”觀點下的數學活動[J].小學數學教師，2016（6）.

（責編 金 鈴）endprint