直升機人機耦合誘發振蕩分析及研究

徐鵬輝，鞠艷秋，齊 馳

(陸軍航空兵學院，航電與兵器工程系，北京 101123)

直升機人機耦合誘發振蕩分析及研究

徐鵬輝，鞠艷秋，齊 馳

(陸軍航空兵學院，航電與兵器工程系，北京 101123)

針對直升機飛控系統和駕駛員在回路所引起的人機耦合振蕩問題，提出了閉環穩定性分析方法。以某型直升機縱向辨識模型為基礎，結合McRuer駕駛員模型和設計的增穩系統，構建了完整的人機耦合分析模型。綜合運用經典控制理論中的基本分析方法并結合實際背景，研究了直升機固有模態的根軌跡以及時域、頻域特性，對比分析了人機耦合誘發振蕩的表現、原因。同時，從控制器設計和駕駛員操縱兩個環節分析，提出了解決人機耦合誘發振蕩的可行措施。仿真結果表明，所提出的人機耦合誘發振蕩的分析方法可以定性、定量分析人機耦合振蕩的物理本質并有效地解決研究問題，在飛控設計和飛行操縱應用中具有理論參考意義。

人機耦合；飛控系統；穩定性分析

0 引言

在現代直升機設計中，為獲得良好的操縱品質，高增益寬頻帶的飛控系統已成為先進直升機設計的重要目標，這也是性能優越的直升機的必然要求，也是未來直升機設計的發展趨勢。然而，當駕駛員與飛控系統同時在直升機控制回路時，飛控系統的設計必須考慮駕駛員在閉環系統的影響，否則，直升機閉環系統的性能可能會被削弱，甚至會誘發人機耦合振蕩，威脅飛行安全，同時損害直升機性能并影響直升機對規定作戰任務的完成情況，造成戰時的巨大損失。因此，研究人機耦合誘發振蕩的原因并提出可行性的解決措施對如何在新時期環境下發揮直升機的最佳性能，保證駕駛員安全操縱具有十分重大的意義。

為分析駕駛員在操縱回路的影響，20世紀40年代，學術界已經開始了駕駛員建模的研究[3]，目前已比較成熟。如McRuer提出了穿越頻率模型[4，5]，該模型表征了駕駛員在操縱回路的開環總傳遞函數具有H(s)=ωcge-τe,s/s的頻率特性(其中，ωc為穿越頻率，τe為等效滯后時間)，駕駛員通過主動操縱調整增益，使ωc接近最高截止頻率，保證了閉環系統的穩定性。該模型通過試驗驗證是一個有效的模型，在人機振蕩分析中被廣泛采用[2]。Hess提出了內外環結構模型[6,7]，該模型以駕駛員的視覺感知、神經肌肉系統感知以及前庭系統感知為反饋信號，描述了駕駛員雙閉環反饋主動操縱的人機交互行為。Mayo建立了生物力學饋入模型[8]，該模型表征了人機耦合振蕩的交互傳遞行為，即直升機的振動通過駕駛桿以被動方式傳遞給駕駛員，而駕駛員通過生物力學饋入的形式由駕駛桿再傳遞回直升機，該模型實質上是一個被動操縱模型。一般情況下，由駕駛員主動操縱引起的振蕩屬于低頻范圍，通常在1～2Hz左右；而由駕駛員被動操縱引起的振蕩屬于高頻范圍，通常在2～8Hz[2]。

對于直升機人機耦合問題的研究，文獻[9]基于Mayo生物力學饋入駕駛員模型，分析了由于駕駛員被動操縱而誘發的直升機垂向圓錐模態不穩定現象。文獻[10]和文獻[11]在文獻[9]的基礎上，結合McRuer穿越頻率模型和Mayo生物力學饋入模型，開展了直升機垂向振蕩的時域分析，同時比較了頻域的Nyquist曲線特性，驗證了其建立的復合駕駛員模型的有效性。然而，文獻[9]-[11]的閉環建模中并未考慮直升機實際的飛控系統。Hess基于內外環結構駕駛員模型，針對不同飛行任務，如著艦、懸停、加速/減速等，分析了不同的人機耦合振蕩案例[12-15]，其主要采用了時域仿真，對于人機耦合振蕩的內在機理缺乏足夠的討論。文獻[16]構建了直升機不同飛行任務的駕駛員工程模型，并提出了與McRuer穿越頻率模型等效的換算方法。文獻[17]分析了靜不穩定電傳飛機作動器速率限制引起的駕駛員誘發振蕩問題，建模中的駕駛員模型處理為簡單的增益環節，討論了駕駛員操縱增益和作動器速率限制值對閉環穩定性的影響。

以上文獻針對直升機人機耦合問題的研究主要是結合不同的駕駛員模型和直升機動力學模型構建人機耦合閉環開展的分析。然而，文獻中的閉環模型很少包含有飛控系統，McRuer認為“產生人機耦合的主要原因是飛控設計失敗”[1]，因此，拋開飛控系統單獨討論由駕駛員操縱誘發振蕩的觀點存在一定的片面性。盡管Hess在建模中包含了飛控系統，但其僅采用時域分析法，很難直觀揭示人機耦合問題的本質。同時，文獻中很少采用頻域法、根軌跡法等多種分析方法從不同角度開展直升機人機耦合的穩定性和魯棒性分析。因此，本文結合直升機駕駛員和飛控系統兩個主要人機耦合誘發因素，采用時域分析法、頻域分析法、模態根軌跡分析法等經典控制理論中的常用分析方法，對人機耦合振蕩的原因及人機耦合閉環的穩定性開展研究，并在此基礎上，結合實際情況提出解決人機耦合誘發振蕩的可行性措施。

1 直升機人機耦合模型

為便于分析問題的本質，本文對直升機人機耦合模型做如下簡化：

1) 采用直升機單通道模型，不考慮通道間的耦合，為盡可能保證仿真的真實度，采用某型直升機縱向辨識模型作為研究對象；

2) 設駕駛員的飛行任務為前飛縱向姿態保持，不考慮其它通道的操縱及影響；

3) 設前飛時操縱采用增穩模式，縱向通道的控制響應類型為RCAH(Rate Command Attitude Hold)模式。

直升機人機耦合閉環結構框圖如圖1所示。圖中，飛控系統模型為C，該控制器為P控制器并以俯仰角θ為反饋信號；直升機機體模型為G；r為駕駛員根據姿態保持任務調整操縱策略以及駕駛員模型輸出的疊加信號；直升機的控制輸入u是駕駛員操縱指令和負反饋輸入之和的增穩運算輸出。同時，閉環系統內部響應造成的載荷干擾為d1，外界對直升機的擾動(如陣風等)為d2。

閉環系統的建模主要包括直升機建模、駕駛員建模以及飛控系統的建模，以下對各環節的具體建模過程進行分析。

1.1直升機模型

由文獻[18]，某型直升機縱向辨識模型傳遞函數為：

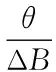
該辨識模型不僅能準確反映機體俯仰角θ與駕駛桿縱向操縱量(百分比)的直接對應關系，而且能反映出直升機的具體模態特性。傳遞函數中存在與擺振響應-控制輸入對相關聯的復數極點很接近的復數零點，反映了耦合的揮舞-擺振-機身系統動態的關鍵特征。等效時間延遲表示已知的控制系統液壓和傳動滯后。

1.2駕駛員模型

由于McRuer駕駛員模型簡潔成熟，且物理含義明確，所以采用該模型作為人機耦合駕駛員模型，其傳遞函數如下[5]：

式中，s為Laplace算子；tpl為與神經傳導和刺激相關的傳遞時間延遲，通常取值范圍為0.13～0.30；1/(TNs+1)為手臂的神經肌肉延遲等效，表示駕駛員操縱速率不高于該極點，通常取值為0.10；kpl為駕駛員操縱增益，是實現最優操縱所要調整的參數，通常取值范圍為1～100；TL為駕駛員對操縱過程預測需要的超前補償時間常數(TL≠TN)，反映了駕駛員精神負荷的大小，通常取值范圍為0～2.5；Tl為中樞信息的傳遞和加工過程時滯，反映了駕駛員體力負荷的大小，通常取值范圍為0～20；kplg(TLs+1)/(Tls+1)是模型的可調參部分，駕駛員根據飛行狀態實時調節，相當于一個超前-滯后環節。駕駛員在回路的閉環帶寬通常低于4rad/s，如果存在不穩定模態頻率高于閉環帶寬4rad/s，駕駛員將很難采取校正動作。

1.3飛控系統模型

為構建完整的閉環系統且保證控制器設計的合理性，本文設計了飛控增穩系統，其控制結構為：

式中，控制器的標稱參數為kp=-0.27838。

內環增穩回路Gin對直升機機體的控制響應如圖2所示。從系統的階躍響應結果可以分析得出，此時系統超調量為191%，穩態誤差為0.5323，表明系統產生的超調量和靜差較大，且系統初始狀況下還會出現較為劇烈的振蕩；然而從系統根軌跡和頻域響應的MATLAB分析結果可以發現雖然該系統最后趨于穩定，但很明顯的是，無論從穩態響應還是動態響應方面，系統都還有待改進。這表明采取P型的飛控系統并不能很理想化地使系統保持很好的穩定性。因此，為保證直升機系統穩態特性與動態特性都得到較好的兼顧，飛控系統仍有待改進，以解決系統穩定性與穩態誤差的矛盾，使系統的整體性能更為優化。

2 人機耦合誘發振蕩原因分析

2.1時域分析法

加入駕駛員模型后對含有增穩系統的直升機機體系統的響應如圖3所示。下面根據仿真結果以及經典控制理論中的三種分析方法，即時域分析法，根軌跡分析法，頻域分析法，并結合實際背景分析產生人機耦合誘發振蕩的原因。

根據經典控制理論中的時域分析方法，對一個給定系統的分析主要分為穩態響應分析和動態響應分析，穩態過程表征的是系統的輸出量復現輸入量的程度，提供有關穩態誤差的信息，通常用穩態誤差來描述。而動態特性在此基礎上還反映了系統的阻尼情況和響應速度等信息，重點強調的是系統在調節過程中的狀態參量指標。一般而言，要求自動控制系統具有“穩、準、快”三大特性，通常用上升時間tr、調節時間ts、超調量σ、峰值時間tp以及穩態誤差Δ來衡量系統的穩態與動態特性。

通常情況下，采取階躍響應信號作為控制系統的典型輸入信號對各種控制系統的特性進行比較和研究。觀察圖3中的階躍響應曲線，很明顯在接入駕駛員模型的含有P控制器的機體中，系統在初始階段便存在發散狀態，即通常所說的不穩定狀態，且最大振幅竟為最終穩定狀態的近乎2倍，超調量達到61.5%。這樣的不穩定狀態就是人機耦合誘發振蕩在時域中的表現，也即為產生振蕩的原因。由圖像可以看出，系統的上升時間為0.552s，調節時間為293s，由于駕駛員延遲環節模型的引入，系統在初始階段便開始產生振蕩，振蕩的劇烈程度隨時間逐漸減小，直至大約293s后才逐漸進入平穩狀態。那么這樣的振蕩必然會對系統性能產生不良影響，尤其是在直升機系統剛開始投入工作時產生的劇烈振蕩甚至可能會威脅駕駛員的生命安全,且調節時間過長，很容易引發危險事故。由文獻[1]，結合實際背景，駕駛員的動態特性通常可以認為是一種純增益，在這種情況下對于整個直升機系統而言，系統的響應速度增大，上升時間、調節時間減少，動態特性較為理想，例如在圖3中的階躍響應所示的結果，但不可避免地導致超調量和穩態誤差的增大，最終引發不穩定狀態，也即通常所說的人機耦合誘發振蕩趨勢。此外，我們可由階躍響應看出，此時系統的終值為0.841，這說明系統依然存在靜差，也就說明系統無法最終達到非常精確的穩定狀態。

2.2根軌跡分析法

由文獻[2]，對于系統增益的穩定性分析而言，直升機的運動模態可以被認為是各種模態綜合作用的表現，每一種模態都含有其特性，例如模態頻率、阻尼、對響應的抗干擾能力等等，那么直升機的實際運動狀態也將由這些模態的特性所決定。通過觀察模態根軌跡就可以根據已知的開環零極點分布確定當系統參數變化時，閉環極點隨參數變化的軌跡，進而可以研究閉環系統極點分布變化的規律。而且用根軌跡法只要進行簡單計算就可得知系統參數變化對閉環極點的影響趨勢。這種定性分析尤其在研究系統性能和提出改善系統性能的合理途徑方面特別有意義。

觀察圖4中所展示的接入駕駛員時系統的模態根軌跡圖可以發現，系統此時的根軌跡有處于復平面右半平面的部分，且存在閉環極點，分別位于虛軸和右半平面，由根軌跡法和勞斯判據及其與時域的聯系可知系統此時有振蕩響應，處于不穩定狀態。由文獻[2]，對照此時系統模態可知，此時系統具有長周期模態和俯仰振蕩模態， 由長周期模態特性可知此時系統阻尼降低，容易引發不穩定狀態，且伴隨著機體處于以上兩種模態時，會出現機體重心發生改變，對應的力矩改變也會使直升機狀態發生變化，產生與短周期模態相反的現象。因此從根軌跡的復平面上看，人機誘發振蕩的原因也非常顯而易見，即由于機體模態對應發生了改變導致直升機的整體狀況發生了變化，也容易誘發人機振蕩。

2.3頻域分析法

那么由頻域穩定性判據，該人機系統為非最小相位系統，由文獻[22]結合圖5、圖6中系統的伯德圖及奈奎斯特曲線得知，此時系統的相角裕度為-19.3deg，幅值裕度為-25.8dB，均為負值，且由奈奎斯特穩定性判據得R=P-Z也不等于零，因此從頻域穩定性的角度來看，此時系統也出現了不穩定狀態，即出現了人機誘發振蕩。

根據文獻[1]，通常在實際飛行過程中，在駕駛員試圖調整系統增益值時以及在為克服系統頻域內的額外延時所造成的相角減少而增加低頻段的超前補償校正時以及由于駕駛員自身的生物力學對駕駛桿的作用試圖增加人機系統穩定性時所導致的低頻段內的振蕩現象，都是引發人機耦合誘發振蕩的常見原因。

以上分別從經典控制理論中的時域分析法、根軌跡模態分析法和頻域分析法，結合實際背景，從不同角度對人機耦合誘發振蕩的原因進行了分析。那么針對產生的人機誘發振蕩，如何采取合理可行的方式加以消除或緩解，就成了亟待解決的重要問題。

3 解決人機耦合誘發振蕩的措施

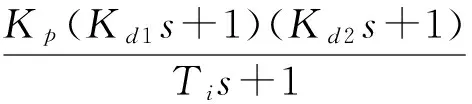
4 結 論

基于以上仿真設計與分析過程，可得到以下結論：

1)在實際飛行過程中，由于駕駛員操縱原因和機體本身狀態的改變等原因，容易引發人機耦合誘發振蕩，在控制系統原理中的時域、頻域、模態根軌跡中都有其具體表現，通過結合應用經典控制理論中的分析方法，可以定性定量地對人機耦合誘發振蕩問題進行原因分析。

2)在采取多角度的經典控制理論分析方法的基礎上，結合實際背景，可以對人機耦合誘發振蕩問題進行較為詳細、充分的研究與解釋，從而比較深刻地揭示出這一問題的本質原因。

3)仿真設計結果表明，通過完善飛控系統并斷開人工操作環節，可以有效地緩解人機耦合誘發振蕩問題，使直升機人機系統保持較為穩定的狀態，取得較為良好的效果。

4)選取比較具有代表性的機型和飛控系統以及相應的駕駛員模型，對于精確的分析過程和最終結論的得出具有十分重要的參考意義。

[1] McRuer D T. Aviation Safety and Pilot Control: Understanding and Preventing Unfavourable Pilot-Vehicle Interactions[M]. Washington, DC: National Academy Press, 1997.

[2] Pavel M D, Jump M, Vu B D, et al. Adverse rotorcraft pilot couplings-Past, present and future challenges[J]. Progress in Aerospace Sciences, 2013, 62(1): 1-51.

[3] Tustin A. The nature of the human operator's response in manual control and its implications for controlled design[J]. Journal of IEE, 1947, 94(1): 190-202.

[4] McRuer D T, Jex H R. A Review of Quasi-Linear Pilot Models[J]. IEEE Transactions on Human Factors in Electronics, 1967,8(3): 231-249.

[5] McRuer D T, Krendel E S. Mathematical Models of Human Pilot Behavior[R]. AGARD AG-188, 1974.

[6] Hess R A. Theory for Aircraft Handling Qualities Based Upon a Structural Pilot Model[J]. Journal of Guidance, Control, and Dynamics, 1989, 12(6): 792-797.

[7] Hess R A. Simplified Approach for Modelling Pilot Pursuit Control Behaviour in Multi-Loop Flight Control Tasks[J]. Journal of Aerospace Engineering, 2006, 220(2): 85-102.

[8] Mayo J R. The involuntary participation of a human pilot in a helicopter collective control loop[C]// 15th European Rotorcraft Forum, Amsterdam, The Netherlands, 1989:1-12.

[9] Quaranta G，Masarati P, Venrooij J. Impact of pilots' biodynamic feedthrough on rotorcraft by robust stability[J]. Journal of Sound and Vibration, 2013, 332(1): 4948-4962.

[10] Masarati P, Quaranta G, Bernardini A，et al. Voluntary Pilot Action Through Biodynamics for Helicopter Flight Dynamics Simulation[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(3): 431-441.

[11] Muscarello V, Quaranta G, Masarati P. The role of rotor coning in helicopter proneness to collective bounce[J]. Aerospace Science and Technology, 2014, 36(1): 103-113.

[12] Hess R A. Modeling Human Pilot Adaptation to Flight Control Anomalies and Changing Task Demands[J]. Journal of Guidance, Control, and Dynamics, Article in Advance, 2015, 6(1): 1-12.

[13] Hess R A. Modeling the Pilot Detection of Time-Varying Aircraft Dynamics[J]. Journal of Aircraft, 2012, 49(6): 2100-2104.

[14] Hess R A, Marchesi F. Analytical Assessment of Flight Simulator Fidelity Using Pilot Models[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(3): 760-770.

[15] Hess R A. Simplified Technique for Modeling Piloted Rotorcraft Operations Near Ships[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1339-1349.

[16] 楊松山. 直升機駕駛員模型研究[J]. 飛行力學, 1993, 11(4):42-47.

[17] 曹啟蒙，李穎暉，徐浩軍. 基于線性矩陣不等式的電傳飛機人機閉環系統穩定域[J]. 航空學報, 2013, 34(1): 19-27.

[18] Tischler M B. System identification requirements for high-bandwidth rotorcraft flight control system design[J]. Journal of Guidance, Control, and Dynamics, 1990, 13(5): 835-841.

[19] Zhou K M, Doyle J C, Glover K，著，毛劍琴, 鐘宜生, 等，譯.魯棒與最優控制[M].北京: 國防工業出版社, 2006.

[20] US Army AMCOM. Aeronautical design standard ADS33E-PRF, performance specification, handling qualities requirements for military rotorcraft[S]. Redstone, Alabama: ASMC N/A, 2000: 76-77.

[21] Chen R T N, Hindson W S. Influence of High-Order Dynamics on Helicopter Flight-Control System Bandwidth[J]. Journal of Guidance, Control, and Dynamics, 1986, 9(2): 190-197.

[22] 鄭昕亮.線性非最小相位系統特性的研究[J]，山東工業技術，2015(2)：204-204.

TheAnalysisoftheHelicopterPIOandtheResearchoftheSolutions

XU Penghui , JU Yanqiu , QI chi

(Department of Helicopter Avionics and Weapon Engineering, Army Aviation Institute, Beijing 101123, China)

Closed-loop analysis method was proposed for pilot induced coupling with helicopter flight control system in closed loop. Combining with the longitudinal identification model of a certain helicopter, McRuer pilot model, and the designed stability augmentation system, frequency domain model was established for pilot induced coupling analysis. By combining the basic analytical methods of the classical automatic control theory and the real backgrounds, the properties of the root locus and the characteristics of the time domain as well as the frequency domain were studied and the properties as well as the reasons of the PIO were also analyzed in comparison. Meanwhile, feasible measures to solve the PIO were discussed considering the controller design and pilot's manipulation. Results showed that the analysis method proposed could not only reveal the physical nature of PIO qualitatively, but also quantitatively, which have theoretical reference significance in both flight control system design and pilot's manipulation applications.

pilot induced coupling; flight control system; stability analysis.

2017-03-02

徐鵬輝(1994-)，男，山東省龍口市人，在讀本科生，主要研究方向：飛行器動力學與設計。

1673-1220(2017)04-006-07

V249.122

A