勻強電場中四個重要結論的推導及其運用

江西 徐亮亮 江秀梅 劉大明

解題之路隱荊棘，撥開云霧見光明——四個結論引路。

勻強電場中四個重要結論的推導及其運用

在高考物理試題中，力電綜合題是每年必考的壓軸題型。其中，力學與電場綜合也是非常重要的，尤其以勻強電場為背景命制綜合試題較多。

本文主要研究勻強電場，給出了勻強電場中四個重要而好用的結論，以饗讀者。

【重要結論1】在勻強電場中，所有平行(包括同一直線上)且相等線段兩端點電勢差相等。

【證明】如圖1所示，在勻強電場中，任一一束平行線確定下來，則它們與電場線之間的夾角θ為確定值。同理，在這束平行線中的任一直線上，取長度為l的任一線段AB，電荷量為q的點電荷沿直線從A點移到B點，則電場力做功都為確定值，即W=qUAB=qElcosθ。于是有UAB=

Elcosθ，其中E為勻強電場的場強。

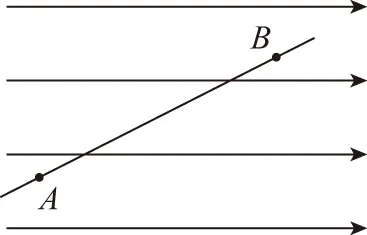
圖1

根據重要結論1，極容易推導一系列其他重要結論，姑且稱它們為重要推論：

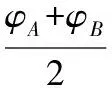
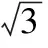
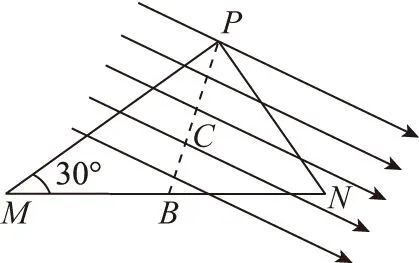
圖6

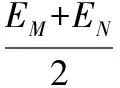
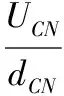
七、場強疊加法

庫侖定律的適用范圍是真空中的點電荷，而實際帶電體，如帶電圓盤、帶電導線等產生的場強的求解常常要用到場強的對稱性和疊加原理才能順利求解。

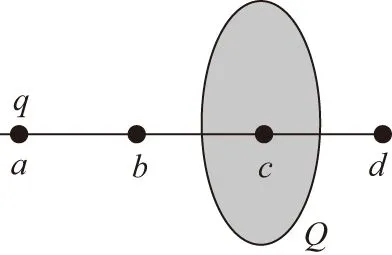
圖7

【例7】(2013新課標全國卷Ⅰ)如圖7所示，一半徑為R的圓盤均勻分布著電荷量為Q的電荷，在垂直于圓盤且過圓心c的軸線上有a、b、d三個點，a和b、b和c、c和d間的距離均為R，在a點處有一電荷量為q(qgt;0) 的固定點電荷，已知b點處的場強為零，則d點處場強的大小為(k為靜電力常量)

( )

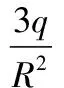
【解析】b和d處的場強都是點電荷和圓盤產生的場強的疊加，而b和d又關于圓盤對稱，圓盤在b、d兩點處產生的場強大小相等、方向相反。點電荷在b和d兩點處產生的場強用庫侖定律即可得到。

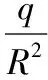
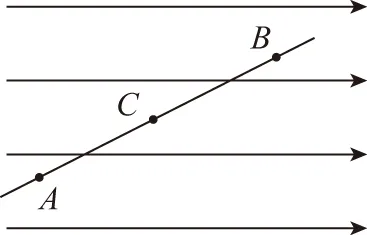
圖2

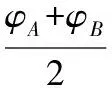
【推論2】如圖3所示，在勻強電場中，四邊形ABCD為平行四邊形，A、B、C、D四點的電勢分別為φA、φB、φC、φD，則φA-φB=φD-φC或φA-φD=φB-φC。

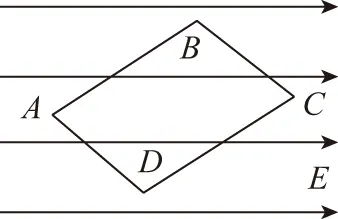
圖3

【證明】AB與DC平行且相等，根據重要結論2，得到φA-φB=φD-φC；同理，亦有φA-φD=φB-φC。

【例1】如圖4所示，在一勻強電場區域中，有A、B、C、D四點恰好位于一長方形的四個頂點上，已知A、B、C三點電勢分別為φA=2 V，φB=4 V，φC=0，則D點電勢φD為________。

圖4

【解析】四邊形ABCD為長方形，根據推論2，有：

φA-φB=φD-φC，即φD=φA-φB+φC=-2 V。

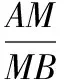
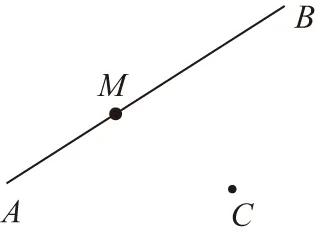
圖5

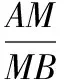
【重要結論3】等勢面(或等勢線)與電場線垂直，沿著電場線方向電勢越來越低。

【例2】在例1基礎上，畫出勻強電場的一條電場線。

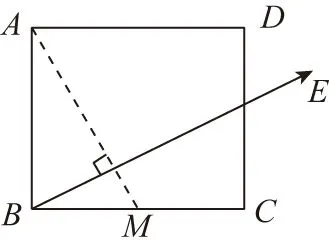
圖6

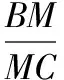
【重要結論4】在勻強電場中有一個圓，其圓面與電場線平行。那么，圓上的點與圓心的電勢差遵循余弦關系，即UOA=Ucosθ(如圖7所示)。其中，θ為半徑OA與電場線之間的夾角，U由勻強電場的強度E和圓半徑的長度R決定，即U=ER。

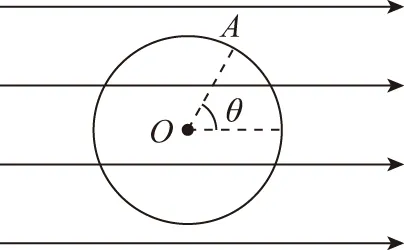
圖7

【證明】設一個電荷量為q的點電荷沿半徑方向從O點移到A點，則電場力做功為W=qUOA=qERcosθ，令U=ER，得到UOA=Ucosθ。

特別指出，U實際上是與電場線平行的半徑線段兩端點的電勢差，即θ=0時，UOA=U。

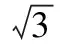
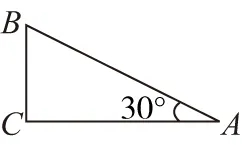
圖8

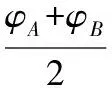
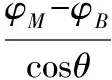
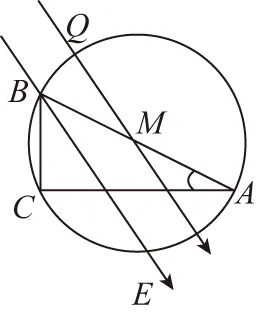
圖9

【答案】3 5

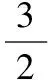
(1)無電場時，小球到達A點時的動能與初動能的比值；

(2)電場強度的大小和方向。

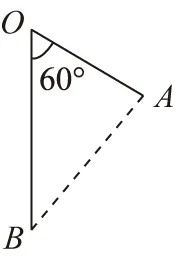
圖10

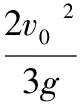
設小球到達A點時的動能為Ek，由動能定理得

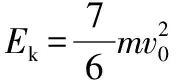
所以Ek∶Ek0=7∶3。

(2)令OA=2L，則OB=3L。設小球帶電后，到達A的動能EkA，到達B的動能為EkB，由動能定理得：

qUOA+mg2Lcos60°=EkA-Ek0

和qUOB+mg3L=EkB-Ek0

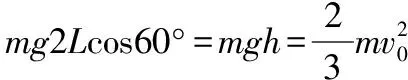
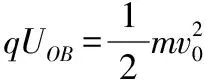
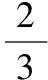
根據重要推論2，OB上可取一點M(OM=2MB)，使得φM=φA，連接AM，即為一條等勢線，不難推知△OAM為等邊三角形。根據重要推論3，知在∠AOB的角平分線為一條電場線，斜向下與豎直方向成30°角，如圖11所示。

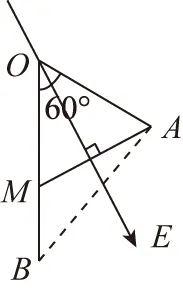
圖11

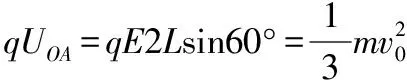
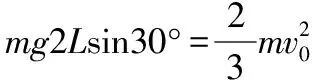
(作者單位：江西省南昌市南鋼學校 江西省撫州市第一中學 江西省撫州市第一中學)

安徽省靈璧縣黃灣中學)