深度剖析“帶電粒子在電磁場中的運動”的三類問題

上海 虞利剛

掌握高頻考點，號準命題“脈搏”。

深度剖析“帶電粒子在電磁場中的運動”的三類問題

帶電粒子在電磁場中運動是高考命題的熱點內容之一，雖然在最近兩年的新課標命題中有一些變化，由壓軸題角色變為選擇題，計算量和綜合度下降，但是考查學生基本方法的目標未變，所以該部分內容在高三復習依然是重中之重。本文就帶電粒子在電磁場中的運動問題進行分析，希望讀者領悟其中的方法。

一、帶電粒子在復合場中運動問題

【例1】如圖1所示，在同時存在勻強電場和勻強磁場的空間中取正交坐標系Oxyz(z軸正方向豎直向上)，一質量為m、電荷量為q的帶正電小球從原點O以速度v沿x軸正方向出發。下列說法正確的是

( )

圖1

A．若電場、磁場分別沿z軸正方向和x軸正方向，小球只能做曲線運動

B．若電場、磁場均沿z軸正方向，小球有可能做勻速圓周運動

C．若電場、磁場分別沿z軸正方向和y軸負方向，小球有可能做勻速直線運動

D．若電場、磁場分別沿y軸負方向和z軸正方向，小球有可能做勻變速曲線運動

【解析】四個選項如表1所示：

表1

【答案】BCD

【感悟】力是改變物體運動狀態的原因，所以分析粒子的運動狀態首先要熟知力的特點。

(1)三種場力：重力大小為G=mg，總是豎直向下，為恒力，做功只取決于初末位置的高度差。是否考慮重力看具體的問題而定。電場力大小為F=qE，方向與場強方向及電性有關，做功只取決于初末位置的電勢差，要注意電荷分為正負電荷兩種，不同電荷受力方向不同。洛倫茲力大小F洛=qvB(v⊥B)，方向用左手定則判定，洛倫茲力永不做功，速度變化時，洛倫茲力也要發生變化。

(2)粒子做直線運動還是曲線運動要看粒子受到的合力方向與速度方向是不是共線。

(3)粒子受到的合力為0，粒子處于平衡狀態；粒子受到的合力為恒力，做勻變速運動，若合力方向與速度共線，為勻變速直線運動；粒子只受重力作用且初速度方向與重力垂直，粒子做平拋運動(類平拋運動是合力恒定且方向與初速度方向垂直)；粒子受到的合力大小恒定，方向總是指向圓心并與速度方向垂直，粒子做圓周運動。

總之，正確分析帶電粒子的受力及運動特征是解決問題的前提。本題中的D項有些同學誤以為速度變化，洛倫茲力變化而排出D項。所以畫出受力分析圖示就清晰了。

二、帶電粒子在有界場中運動問題

( )

圖2

圖3

【答案】D

【總結】(1)直線邊界，如圖4所示，粒子從某一邊界射入磁場時和從同一邊界射出時，速度方向與邊界的夾角相等。

圖4

(2)平行邊界，如圖5所示，存在臨界條件。一種是與邊界線的臨界，甲圖中O1圓對應的軌跡與邊界相切；另一種是與邊界的臨界，甲圖中O2圓對應的軌跡與邊界點相交。

圖5

【例3】(圓形界問題)如圖6所示，圓形區域內有垂直于紙面向里的勻強磁場，一個帶電粒子以速度v從A點沿直徑AOB方向射入磁場，經過Δt時間從C點射出磁場，OC與OB成60°角。現將帶電粒子的速度變為v/3，仍從A點沿原方向射入磁場，不計重力，則粒子在磁場中的運動時間變為

( )

圖6

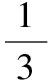
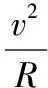
圖7

【答案】B

【總結】(1)帶電粒子沿半徑方向射入圓形磁場的粒子，必沿半徑方向射出。

(2)如圖8所示，粒子速度的偏向角φ等于回旋角α，且等于AC弦與切線的夾角(弦切角)θ的兩倍，即φ=α=2θ。

(3)如圖8所示，相對的弦切角相等，與相鄰的弦切角互補，即：θ+θ′=180°。

圖8

( )

圖9

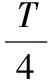
圖10

【答案】AB

【總結】帶電粒子在磁場中運動，常常遇到磁場的有界而產生臨界問題，對于此類問題采用以下兩種方法。

(1)動態放縮法：當帶電粒子射入磁場的方向確定，但射入時的速度v大小或磁場的強弱B變化時，粒子做圓周運動的軌道半徑r隨之變化。在確定粒子運動的臨界情景時，可以以入射點為定點，將軌道半徑放縮，作出一系列的軌跡，從而探索出臨界條件。如圖11所示，粒子進入長方形邊界OABC形成的臨界情景為②和④。

圖11

(2)定圓旋轉法：當帶電粒子射入磁場時的速率v大小一定，但射入的方向變化時，粒子做圓周運動的軌道半徑r是確定的。在確定粒子運動的臨界情景時，可以以入射點為定點，將軌跡圓旋轉，作出一系列軌跡，從而探索出臨界條件，如圖12所示為粒子進入單邊界磁場時的情景。

圖12

三、帶電粒子在組合場中運動問題

【例5】(2017·山東省濰坊模擬)在如圖13所示的坐標系中，第一和第二象限(包括y軸的正半軸)內存在磁感應強度大小為B、方向垂直xOy平面向里的勻強磁場；第三和第四象限內存在平行于y軸正方向、大小未知的勻強電場。p點為y軸正半軸上的一點，坐標為(0，l)；n點為y軸負半軸上的一點，坐標未知。現有一帶正電的粒子由p點沿y軸正方向以一定的速度射入勻強磁場，該粒子經磁場偏轉后以與x軸正半軸成45°角的方向進入勻強電場，在電場中運動一段時間后，該粒子恰好垂直于y軸經過n點。粒子的重力忽略不計。求：

圖13

(1)粒子在p點的速度大小；

(2)第三和第四象限內的電場強度的大小；

(3)帶電粒子從由p點進入磁場到第三次通過x軸的總時間。

【解析】粒子在復合場中的運動軌跡如圖14所示

圖14

(1)由幾何關系可知

rsin45°=l

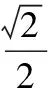
由類平拋運動規律有

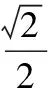
聯立以上方程解得

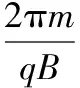
故粒子從開始到第三次通過x軸所用時間為

【總結】常見的組合場問題主要表現為以下兩種情形。

(1)先電場后磁場模型

表2

表3

(2)先磁場后電場模型

對于粒子從磁場進入電場的運動，常見的有兩種情況：①進入電場時粒子速度方向與電場方向相同或相反；②進入電場時粒子速度方向與電場方向垂直。(如圖15所示)

圖15

上海市七寶中學)