概率統計中與分布列有關的問題的探討

廣西 包日勇

概率統計中與分布列有關的問題的探討

廣西 包日勇

新課標高考中概率統計的大題往往都是概率與統計的結合，既含有統計方面的知識，也有概率的計算，理科中更注重分布列的研究，而超幾何分布和二項分布是最為常考的兩種概率分布.如何根據已知條件，快速確定概率分布的類型，熟練掌握這兩種概率分布的解題要點，是決勝高考的關鍵.

一、抓住關鍵字眼，準確把握分布類型

概率統計的大題往往文字較多，篇幅較長，在解題過程中，要學會抓住關鍵字眼，快速準確地判斷出概率和分布列的類型，切忌生搬硬套.

【例1】為了降低汽車尾氣的排放量，某廠生產甲、乙兩種不同型號的節排器，分別從甲、乙兩種節排器中隨機抽取100件進行性能質量評估檢測，綜合得分情況的頻率分布直方圖如圖所示：

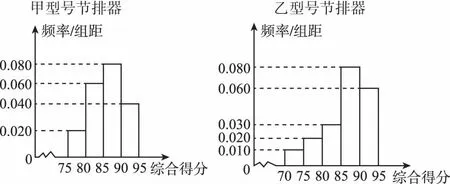
節排器等級及利潤如表格

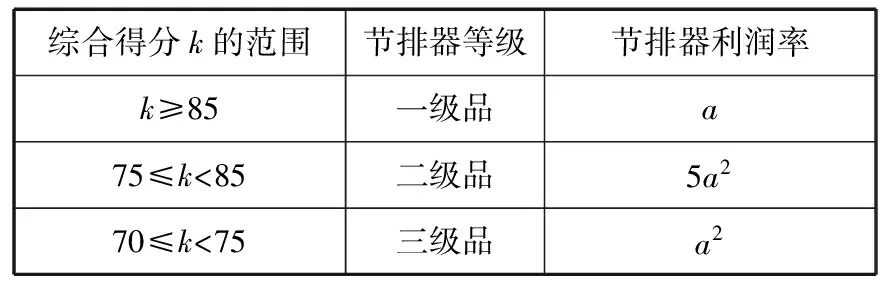
綜合得分k的范圍節排器等級節排器利潤率k≥85一級品a75≤klt;85二級品5a270≤klt;75三級品a2

(Ⅰ)將頻率分布圖中的頻率視為概率，則

(ⅰ)若從甲型號節排器中按節排器等級用分層抽樣的方法抽取10件，再從這10件節排器中隨機抽取3件，求至少有2件一級品的概率；

(ⅱ)若從乙型號節排器中隨機抽取3件，求二級品數ξ的分布列及數學期望E(ξ)；

(ⅲ)從抽出的乙型號節排器中隨機抽取3件，求二級品數η的分布列及數學期望E(η)；

(Ⅱ)從長期來看，投資哪種型號的節排器平均利潤較大？

分析：第(ⅱ)問中從乙型號節排器中隨機抽取3件，求二級品數ξ的分布列，因為題目中有“將頻率分布圖中的頻率視為概率”，說明可認為乙型號節排器有無數多個，為對無限總體的研究，可以看作做了3次獨立重復試驗，研究取得二級品這一事件發生的次數問題，符合二項分布.第(ⅲ)問中從抽出的100件乙型號節排器中隨機抽取3件，即“在(從)……(有限個中)選取……”，則為對樣本的研究，為有限總體不放回抽樣，研究二級品數這一事件發生的問題，則考的是古典概型，也就是相當于100個產品中含有25個二級品，從中抽出3個，研究其中所含的二級品數問題，符合超幾何分布.

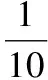
(ⅱ)若從乙型號節排器中隨機抽取3件，從生產線上下來的乙型號節排器有無數多個，可以看作一個獨立重復過程，把取得二級品這一事件看作A，相當于做了3次獨立重復試驗，研究事件A發生的次數問題，為二項分布.

所以ξ～B(3,0.25)，E(ξ)=3×0.25=0.75.

(ⅲ)從抽出的100件乙型號節排器中隨機抽取3件，屬于有限總體不放回抽樣，研究其中所含的二級品數問題，為超幾何分布.

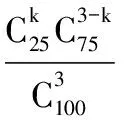
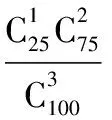
(Ⅱ)設X為投資甲型號節排器獲得的平均利潤，Y為投資乙型號節排器獲得的平均利潤，由題意得出甲、乙的分布列如下：

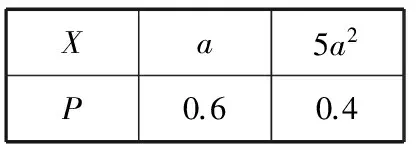
Xa5a2P0．60．4

甲：E(X)=0.6a+2a2

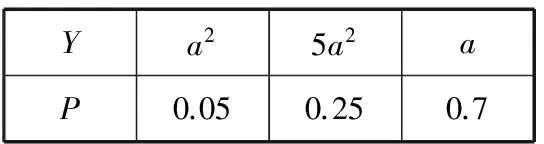
Ya25a2aP0．050．250．7

乙：E(Y)=0.7a+1.3a2

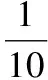
評析：本題在解題過程中，認真弄清題意，確定類型，區分這兩種概率計算，分析所研究的分布列滿足的條件，才能順利求解.

解題要點一：與統計相結合的概率題目，通常以抽樣與頻率分布直方圖相結合為背景，若有“頻率視為概率”的字眼，則為對無限總體的研究，有 “實驗具有重復性”，“有放回抽樣”等字眼，則整個過程為一重復過程；有“實驗次數多”字眼，雖然對總體抽樣時不放回，但在大量的情況下可看作獨立重復，則考的是獨立重復試驗，若研究某一事件有多少次發生問題，一般為二項分布.

解題要點二：若有“在(從)……(有限個中)選取……”的字眼，則為對樣本的研究，為有限總體，若采用不放回抽樣，是古典概型，若研究恰好有某一事件發生的問題，則考的是古典概型，通常為超幾何分布.

二、審清題意，分析清楚概率事件

在解題過程中，除了要抓關鍵字眼外，還要注意分析要研究的概率事件，正確判斷隨機變量的取值.有些題目雖然表面上看滿足超幾何分布或二項分布的前提，但所研究的概率事件卻并不相同.

【例2】(2015·福建)某銀行規定，一張銀行卡若在一天內出現3次密碼嘗試錯誤，該銀行卡將被鎖定，小王到銀行取錢時，發現自己忘記了銀行卡的密碼，但是可以確定該銀行卡的正確密碼是他常用的6個密碼之一，小王決定從中不重復地隨機選擇1個進行嘗試.若密碼正確，則結束嘗試；否則繼續嘗試，直至該銀行卡被鎖定.

(Ⅰ)求當天小王的該銀行卡被鎖定的概率；

(Ⅱ)設當天小王用該銀行卡嘗試密碼次數為X，求X的分布列和數學期望.

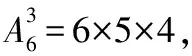
解：(Ⅰ)設“當天小王的該銀行卡被鎖定”的事件為A，則

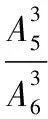
(Ⅱ)依題意得，X所有可能的取值是1，2，3，

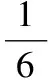
所以X的分布列為

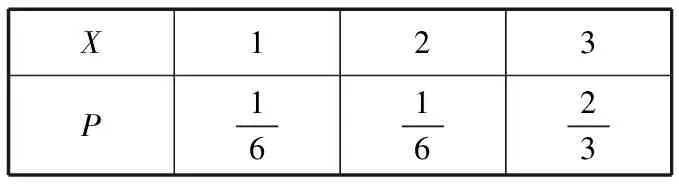
X123P161623

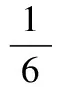
評析：題目中屬于有限總體，不放回的抽樣，但研究的是嘗試密碼次數，這與超幾何分布研究的概率事件不同.因此在解題中既要注意分析前提條件，也要看清概率事件才行.

解題要點三：在概率統計解題中，仔細審題，注意分析要研究的概率事件，正確判斷隨機變量的取值，超幾何分布和二項分布有著不同的前提，超幾何分布是針對有限總體不放回，二項分布是針對有放回或無限總體情形.但也不能只看到這一前提就判斷出分布列的類型，要清楚“從含有M件次品的N件產品中任取n件，其中所含次品數問題”，才服從超幾何分布；而“在n次獨立重復試驗中，事件A發生的次數問題”才服從二項分布.若“從含有M件次品的N件產品中任取n件”，但研究的不是次品數問題，則也不是超幾何分布.同樣若“在n次獨立重復試驗中”，但不是研究某事件發生的次數，則也不是二項分布.因此解題中還應注意題目中要研究的概率事件是什么.

【例3】廠家在產品出廠前，需對產品做檢驗，廠家將一批產品發給商家時，商家按合同規定也需隨機抽取一定數量的產品做檢驗，以決定是否接收這批產品.

(Ⅰ)若廠家庫房中的每件產品合格的概率為0.8，從中任意取出4件進行檢驗.求至少有1件是合格品的概率;

(Ⅱ)若廠家發給商家20件產品，其中有3件不合格，按合同規定該商家從中任取2件，都進行檢驗，只有2件都合格時才接收這批產品，否則拒收.求該商家可能檢驗出不合格產品數ξ的分布列及期望E(ξ)，并求該商家拒收這批產品的概率.

分析：(Ⅰ)為獨立重復試驗，利用對立事件概率容易得出；(Ⅱ)從含3件不合格品的20件產品中選2件，研究所含不合格品的問題，為超幾何分布.

解:(Ⅰ)記“廠家任取4件產品檢驗，其中至少有1件是合格品”為事件A,

(Ⅱ)ξ可能的取值為0,1,2,

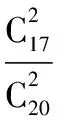
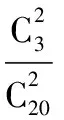
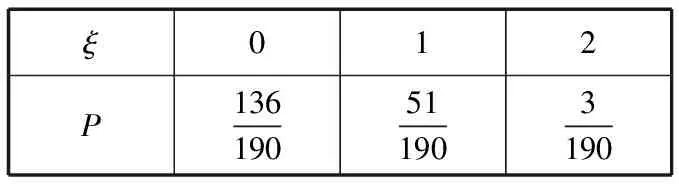
ξ012P136190511903190

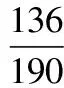
記“商家任取2件產品檢驗，都合格”為事件B，則商家拒收這批產品的概率

評析：認真分析清楚分布列類型就能正確求解，此題想法并不難，但運算量相對大些，容易在時間緊張時算錯，因此在運算時必須講究技巧，可借助期望的計算公式減少運算量，提高運算的準確率.

三、巧妙借助公式，簡化計算提高準確率

概率統計的題目，基本上在分析清楚分布列后都要求計算期望和方差，這是運算量相對較大的地方.熟練掌握二項分布和超幾何分布的期望方差公式及其聯系，對于提高速度和準確率都是有效的.

解題要點四：在與分布列有關的問題，基本上都涉及期望和方差，因此熟記超幾何分布與二項分布的期望和方差公式，對快速正確作答很有幫助.

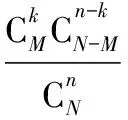
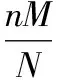
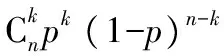
E(X)=np,DX=np(1-p).

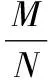
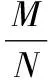
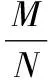
廣西合浦廉州中學)