動(dòng)量和能量綜合四大模型歸納

浙江

汪顯和

三把“金鑰匙”開啟四類“不能再”現(xiàn)象。

動(dòng)量和能量綜合四大模型歸納

汪顯和

動(dòng)量守恒問題是新高考中的一大亮點(diǎn)，這塊曾經(jīng)幾乎被擱置起來的重要的物理學(xué)知識(shí)在新高考中開始顯得極為重要。在考題中往往將動(dòng)量的問題和能量的問題結(jié)合起來，聯(lián)系生活中的情景，形成一類難度較大的綜合題，使得許多同學(xué)在解題過程中感覺難度很大，容易失分。總結(jié)動(dòng)量和能量綜合大題的分析，筆者認(rèn)為此類問題最為關(guān)鍵的核心部分可以歸納為四種模型。相關(guān)的動(dòng)量能量的綜合問題幾乎都是這四種當(dāng)中的某一類或者是幾類合成起來的，具體解題過程中我們只要能夠找出問題的最根本的模型就可能快速、準(zhǔn)確地將問題予以解決。

一、“穿到不能再穿”模型

【例1】如圖1所示，光滑水平面上質(zhì)量為M的木塊在水平面上處于靜止?fàn)顟B(tài)，有一質(zhì)量為m的子彈以水平速度v0擊中木塊并與其一起運(yùn)動(dòng)，求系統(tǒng)所產(chǎn)生的內(nèi)能？

圖1

【解析】取子彈和木塊為參考系。由于地面光滑，故系統(tǒng)的動(dòng)量守恒。取向右為正方向。

根據(jù)動(dòng)量守恒定律有：mv0=(M+m)v

【總結(jié)】這種子彈穿入木塊最后達(dá)到兩者相對(duì)靜止的狀態(tài)，我們總結(jié)為“穿到不能再穿”的模型。子彈打擊木塊的時(shí)間非常短，假如沒有“光滑水平面”的條件，子彈穿入木塊的過程也可以認(rèn)為系統(tǒng)的動(dòng)量守恒，也可以應(yīng)用動(dòng)量守恒定律進(jìn)行求解。

二、“滑到不能再滑”模型

【例2】圖2所示，在光滑的水平面上有一塊質(zhì)量為M的粗糙木板，一質(zhì)量為m的物塊以速度v0滑上木板的左端，物塊與木板的動(dòng)摩擦因數(shù)為μ。要使木塊不會(huì)從木板右端掉下來，則木板的長(zhǎng)度至少要多長(zhǎng)？

圖2

【解析】取物塊和木板為系統(tǒng)研究。由于地面光滑，故系統(tǒng)的動(dòng)量守恒。要使m不會(huì)從M的右端滑下來，臨界的狀態(tài)是m剛好滑到M最右端的時(shí)候兩者相對(duì)靜止，即有共同的速度v。取初速度的方向?yàn)檎较颉?/p>

根據(jù)動(dòng)量守恒定律有：mv0=(M+m)v

在滑動(dòng)過程中系統(tǒng)減少的動(dòng)能轉(zhuǎn)化為內(nèi)能

【總結(jié)】像這種小物塊在木板發(fā)生相對(duì)滑動(dòng)最后達(dá)到兩者相對(duì)靜止的狀態(tài)，我們把它總結(jié)為“滑到不能再滑”的模型。

三、“壓到不能再壓”模型

【例3】如圖3所示，光滑水平面上有質(zhì)量分別為m1、m2的A、B兩物體。靜止物體B左側(cè)固定一處于原長(zhǎng)的輕彈簧，物體A以初速度v0水平向右運(yùn)動(dòng)，接觸彈簧以后將壓縮彈簧，求在壓縮彈簧過程中彈簧的最大彈性勢(shì)能。

圖3

【解析】A、B和彈簧為研究系統(tǒng)。由于地面光滑，故系統(tǒng)的動(dòng)量守恒。由于剛開始的時(shí)候B是靜止不動(dòng)的，A運(yùn)動(dòng)一段時(shí)間后與彈簧接觸，彈簧將會(huì)被壓縮。壓縮的彈簧對(duì)A有向左的力，故A減速，彈簧對(duì)B有向右的力，故B加速。總有一個(gè)時(shí)刻A的速度和B的速度相等，即A、B有共同速度，此時(shí)刻兩者相距最近。此時(shí)的彈簧壓縮量最大，彈性勢(shì)能最大。取向右為正方向。

系統(tǒng)減少的動(dòng)能轉(zhuǎn)化成為彈簧的彈性勢(shì)能。

【總結(jié)】這個(gè)模型中，由于開始A的速度大于B的速度，兩者距離逐漸減小彈性勢(shì)能增大，當(dāng)A的速度小于B的速度時(shí)兩者之間的距離增大彈性勢(shì)能減小；A、B間距離最小，也就是壓到不能再壓的時(shí)候，彈簧的彈性勢(shì)能最大，這就是“壓到不能再壓”模型。對(duì)于這個(gè)模型，假如說A與彈簧接觸后就被粘連，那么可以讓我們同學(xué)分析，A接觸彈簧之后由A、彈簧、B組成系統(tǒng)的運(yùn)動(dòng)的情況，以及能量和動(dòng)量的變化的情況。

四、“升到不能再升”模型

圖4

【例4】如圖4所示，質(zhì)量為M的帶有圓弧曲面的小車靜止在光滑水平面上，另有一質(zhì)量為m的小球以水平速度v0沖上小車的曲面。求m能夠在小車的曲面上上升的最大高度。

所謂就業(yè)觀，具體就是學(xué)生在參加工作選擇某一職業(yè)時(shí)所表現(xiàn)出的一種態(tài)度和觀念，它是學(xué)生對(duì)自己就業(yè)的一種反應(yīng)性傾向，由行為傾向、情感傾向和認(rèn)知傾向三大要素組成。對(duì)大學(xué)生而言，就業(yè)并不意味著就是簡(jiǎn)單地找一份工作，還與學(xué)生后期的人生發(fā)展與職業(yè)理想有著密不可分的必然聯(lián)系。因此，學(xué)生在校期間，形成一種良好的就業(yè)觀是其人生觀、價(jià)值觀和世界觀的重要體現(xiàn)，對(duì)大學(xué)生未來職業(yè)發(fā)展的理想以及就業(yè)認(rèn)知和就業(yè)心態(tài)及其后期在職場(chǎng)上所體現(xiàn)出的態(tài)度和修養(yǎng)也發(fā)揮著決定性作用。

【解析】對(duì)m和M整個(gè)系統(tǒng)而言，m在曲面向上運(yùn)動(dòng)的過程中，M也同時(shí)向右運(yùn)動(dòng)。由于m豎直方向上速度有向上的分量，可以知道系統(tǒng)的動(dòng)量不守恒。但由于水平地面是光滑的，對(duì)系統(tǒng)而言在水平方向上的合力等于零，故系統(tǒng)在水平方向上動(dòng)量守恒。另外從運(yùn)動(dòng)過程可以知道當(dāng)小球在豎直方向上的分速度等于零時(shí)，小球到達(dá)最大高度，此時(shí)小球和小車具有共同的速度。取向右方向?yàn)檎较颉?/p>

根據(jù)動(dòng)量守恒定律可知：mv0=(M+m)v

系統(tǒng)減少的動(dòng)能轉(zhuǎn)化為小球上升過程中所增加的重力勢(shì)能。

【總結(jié)】這個(gè)模型中，小球在上升的過程中，最后豎直方向上的分速度變?yōu)榱悖簿褪钦f在豎直方向的能夠上升的高度達(dá)到最大，我們稱之為“升到不能再升”模型。對(duì)于此類模型往往系統(tǒng)的總動(dòng)量并不守恒，但是在某一個(gè)方向上的動(dòng)量確是守恒的，此時(shí)我們就要利用這個(gè)方向上的動(dòng)量守恒進(jìn)行問題的解決。

以上是動(dòng)量和能量綜合問題的四種核心關(guān)鍵模型。可以看出，動(dòng)量和能量綜合的問題關(guān)鍵在于確定研究的對(duì)象，然后找到動(dòng)量守恒和能量守恒的過程，最后列出動(dòng)量守恒和能量守恒的方程。對(duì)于動(dòng)量守恒定律的關(guān)鍵是根據(jù)問題情境判斷系統(tǒng)動(dòng)量是否守恒，或者是在某一個(gè)方向上動(dòng)量守恒。而能量守恒的關(guān)鍵在于搞清楚物體在運(yùn)動(dòng)過程中是什么能量和什么能量之間的轉(zhuǎn)化，在轉(zhuǎn)化過程中能量的定量關(guān)系如何，最后列出相關(guān)方程。聯(lián)立動(dòng)量守恒和能量守恒的相關(guān)方程，就可以解決問題。具體問題中的動(dòng)量和能量的問題幾乎都在這四種模型之內(nèi)，或者就是這四種中的兩種或多種的組合，解題過程中只要分析清楚問題的情景過程，明確各個(gè)物理過程中的動(dòng)量和能量的相關(guān)情況，逐個(gè)聯(lián)立方程就可解決問題。

圖5

【牛刀小試】如圖5所示，質(zhì)量為m2的小環(huán)穿在光滑水平細(xì)桿上。小環(huán)通過不可伸長(zhǎng)的細(xì)線懸掛著質(zhì)量為m1的木塊。m1和m2處于靜止?fàn)顟B(tài)。質(zhì)量為m0的子彈以初速度v0水平射入木塊并留在其中，求木塊能夠上升的最大高度。

【解析】這個(gè)問題涉及兩個(gè)過程，分別對(duì)應(yīng)兩種模型。

過程一是“穿到不能再穿”的過程。這個(gè)過程中研究對(duì)象取m0和m1。由于作用時(shí)間非常短，兩者之間產(chǎn)生很大的內(nèi)力故子彈和木塊的動(dòng)量守恒。取初速度的方向?yàn)檎较颍O(shè)子彈射入木塊后木塊和子彈的速度為v1，根據(jù)動(dòng)量守恒定律有：m0v0=(m0+m1)v1。

過程二是“升到不能再升”的過程。這個(gè)過程中研究對(duì)象是子彈、木塊和小環(huán)。這個(gè)系統(tǒng)的總動(dòng)量不守恒，但是水平方向上動(dòng)量守恒。當(dāng)木塊上升到最高點(diǎn)時(shí)，小環(huán)和木塊有共同的速度。取向右為正方向。

根據(jù)動(dòng)量守恒定律有：(m0+m1)v1=(m0+m1+m2)v2

在木塊上升過程中，子彈和木塊的重力勢(shì)能增加，系統(tǒng)的動(dòng)能減小轉(zhuǎn)化為重力勢(shì)能

根據(jù)能量守恒定律有：

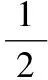
聯(lián)立上述方程可以解得：

即木塊能夠上升的最大高度為

浙江省蘭溪市第一中學(xué))