“一動碰一靜”速度公式的推導與應用

北京

公衍錄(特級教師)

“一動碰一靜”速度公式的推導與應用

公衍錄(特級教師)

從2017年起，全國物理考綱已將選修3-5作為物理高考的必考內容，而彈性碰撞問題一直是高考的熱點。求解該類問題需要的數學運算比較麻煩，但是若應用“一動碰一靜”的速度公式，就可使該類問題的求解變得簡單。

一、“一動碰一靜”速度公式的推導

圖1

如圖1所示，在光滑水平面上，質量為m1、m2的兩球發生對心彈性碰撞，碰撞前的速度分別為v1和零，求兩球碰撞后各自的速度。

二、“一動碰一靜”速度公式的應用

1.直接應用于求解“一動碰一靜”的問題

【例1】(2015·全國卷Ⅰ)如圖2，在足夠長的光滑水平面上，物體A、B、C位于同一直線上，A位于B、C之間。A的質量為m，B、C的質量都為M，三者都處于靜止狀態，現使A以某一速度向右運動，求m和M之間滿足什么條件才能使A只與B、C各發生一次碰撞。設物體間的碰撞都是彈性的。

圖2

【解析】A向右運動與C發生第一次彈性碰撞，碰撞過程中，系統的動量守恒、機械能守恒。設向右為正方向，開始時A的速度為v0，第一次碰撞后C的速度為vC1，A的速度為vA1。由動量守恒定律和機械能守恒定律得:

mv0=mvA1+MvC1①

【答案】ABD

2.間接應用于求解“一動碰一動”的一般彈性碰撞問題

圖3

【例2】(2014·全國卷Ⅰ)如圖3，質量分別為mA、mB的兩個彈性小球A、B靜止在地面上方，B球距地面的高度h=0.8 m，A球在B球的正上方。先將B球釋放，經過一段時間后再將A球釋放。當A球下落t=0.3 s時，剛好與B球在地面上方的P點處相碰，碰撞時間極短，碰后瞬間A球的速度恰好為零。已知mB=3mA，重力加速度大小g=10 m/s2。忽略空氣阻力及碰撞中的動能損失。求：

(1)B球第一次到達地面時的速度；

(2)P點距離地面的高度。

將h=0.8 m代入，求得vB=4 m/s ②

由于碰撞時間極短，重力的作用可以忽略，兩球碰撞前后的動量守恒，總動能保持不變。選豎直向下為正方向，有

設P點距地面的高度為h′，由運動學規律可得

聯立②③④⑤⑥⑦式，并代入已知條件可求得：

h′=0.75 m。

【答案】(1)4 m/s (2)0.75 m

【點評】上面第(2)問在得到④⑤式后，直接代入數字求解，麻煩且容易出錯。可采用以下幾個比較簡單的方法求解。

【解法2】逆向思維法

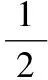
直接應用“一動碰一靜”速度公式可得到B、A球碰撞前瞬間的速度

【解法3】等效法

【解法4】巧選參考系法

由于參考系B球具有對地的速度v2，故碰后瞬間A球對地的速度為

(作者單位：北京市豐臺區豐臺第二中學)

山東省高青縣第一中學)

如果m>M，第一次碰撞后，A與C速度同向，且A的速度小于C的速度，不可能與B發生碰撞；如果m=M，第一次碰撞后，A停止，C以A碰前的速度向右運動(交換速度)，A不可能與B發生碰撞；所以只需考慮m

第一次碰撞后，A反向運動與B發生碰撞。設與B發生碰撞后，A的速度為vA2，應用“一動碰一靜”的速度公式，同理有：

根據題意，要求A只與B、C各發生一次碰撞，應有vA2≤vC1⑥

聯立④⑤⑥式得m2+4mM-M2≥0 ⑦