訓練七 碰撞與動量守恒

《教學考試》物理命題研究中心

訓練七 碰撞與動量守恒

《教學考試》物理命題研究中心

1.(2017·山東省棗莊市質量檢測)質量為60 kg的建筑工人，不慎從高空跌下，由于彈性安全帶的保護，使他懸掛起來；已知彈性安全帶的緩沖時間是1.2 s，安全帶長 5 m，不計空氣阻力影響，g取10 m/s2，則安全帶所受的平均沖力的大小為

( )

A.100 N B.500 N

C.600 N D.1 100 N

2.(2017·安徽省合肥市第一中學高三第三階段考試)如圖所示，F1、F2等大反向，同時作用在靜止與于光滑水平面上的A、B兩物體上，已知兩物體質量關系MA>MB，經過相等時間撤去兩力，以后兩物體相碰且粘為一體，這時A、B將

( )

A.停止運動 B.向右運動

C.向左運動 D.仍運動但方向不能確定

3.(2017·遼寧省本溪市高級中學、大連育明高級中學、大連二十四中高三聯合模擬考試)一位質量為m的運動員從下蹲狀態向上跳起，經Δt時間，身體伸直并剛好離開地面，速度為v，在此過程中，下列說法正確的是

( )

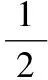
B.地面對他的沖量為mv-mgΔt，地面對他做的功為零

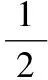
D.地面對他的沖量為mv+mgΔt，地面對他做的功為零

( )

A.碰后小球B的動量大小為PB=3 kg·m/s

B.碰后小球B的動量大小為PB=5 kg·m/s

C.小球B的質量為15 kg

D.小球B的質量為3 kg

5.(多選)(2017·西藏自治區拉薩中學期末)如圖所示，小車AB放在光滑水平面上，A端固定一個輕彈簧，B端粘有油泥，小車AB質量為M，質量為m的木塊C放在小車上，用細繩連接于小車的A端并使彈簧壓縮，開始時AB和C都靜止，當突然燒斷細繩時，C被釋放，使C離開彈簧向B端沖去，并跟B端油泥粘在一起，忽略一切摩擦，以下說法正確的是

( )

A.彈簧伸長過程中C向右運動，同時AB也向右運動

B.C與B碰前，C與AB的速率之比為M∶m

C.C與油泥粘在一起后，AB立即停止運動

D.C與油泥粘在一起后，AB繼續向右運動

6.(2017·黑龍江省牡丹江市第一高級中學月考)光滑水平面上有一質量為M的木板，在木板的最左端有一質量為m的小滑塊(可視為質點)。小滑塊與木板之間的動摩擦因數為μ。開始時它們都處于靜止狀態，某時刻給小滑塊一瞬時沖量，使小滑塊以初速度v0向右運動。經過一段時間小滑塊與木板達到共同速度v，此時小滑塊與木板最左端的距離為d，木板的位移為x，如圖所示。下列關系式正確的是

( )

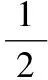
(1)木板B上表面的動摩擦因素μ；

(3)當A滑離C時，C的速度。

9.(2017·遼寧省本溪市高級中學、大連育明高級中學、大連二十四中高三聯合模擬考試)如圖所示，CDE為光滑的軌道，其中ED是水平的，CD是豎直平面內的半圓，與ED相切與D點，且半徑R=0.5 m，質量m=0.1 kg的滑塊A靜止在水平軌道上，另一質量M=0.5 kg的滑塊B前端裝有一輕質彈簧(A、B均可視為質點)以速度v0向左運動并與滑塊A發生彈性正碰，若相碰后滑塊A滑上半圓軌道并能過最高點C，取重力加速度g=10 m/s2，則:

(1)B滑塊至少要以多大速度向前運動；

(2)如果滑塊A恰好能過C點，滑塊B與滑塊A相碰后輕質彈簧的最大彈性勢能為多少？

參考答案

2.A 【解析】根據動量定理得F1t=MAvA，同理F2t=MBvB，F1、F2等大反向，故MAvA=-MBvB，設A的初速度方向為正方向，根據動量守恒定律得MAvA+MBvB=(MA+MB)v，解得v=0，可知粘合體靜止，A項正確。

3.D 【解析】人的速度原來為零，起跳后變化v，以向上為正方向，由動量定理可得I-mgΔt=mv-0，故地面對人的沖量為mv+mgΔt，人在跳起時，地面對人的支持力豎直向上，在跳起過程中，在支持力方向上沒有位移，地面對運動員的支持力不做功，D項正確。

5.BC 【解析】小車、物塊和彈簧組成的系統動量守恒，開始時總動量為零，當彈簧伸長的過程中，C向右運動，則小車向左運動，A項錯誤；規定向右為正方向，在C與B碰前，根據動量守恒得，0=mvC-Mv，解得vC∶v=M∶m，B項正確；因為小車、物塊和彈簧組成的系統動量守恒，開始總動量為零，當C與泥粘在一起時，總動量仍然為零，則小車停止運動，C項正確，D項錯誤。

【解析】(1)當A在B上滑動時，A與BC整體發生作用，由于水平面光滑，A與BC組成的系統動量守恒：

系統動能的減小量等于滑動過程中產生的內能

Q=μmgL②

而Q=ΔEk④

(3)當A滑下C時，設A的速度為vA，C的速度為vC，A與C組成的系統動量守恒:

A與C組成的系統動能守恒：

9.(1)v0=3 m/s (2)Ep=0.375 J

B與A發生彈性碰撞，碰撞過程動量守恒、機械能守恒，以向左為正方向，由動量守恒定律得：

Mv0=Mv1+mv2

聯立并代入數據解得v0=3 m/s。

(2)由于B與A碰撞后，當兩者速度相同時有最大彈性勢能Ep，設共同速度為v，A、B碰撞過程系統動量守恒、機械能守恒，以向左為正方向，由動量守恒定律得：

Mv0=(M+m)v