巧用端點 回避討論
——破解一類“不等式恒成立求參數范圍”問題

山東 郭允遠

巧用端點 回避討論
——破解一類“不等式恒成立求參數范圍”問題

山東 郭允遠

含參數的不等式在給定區間內恒成立，求參數的范圍問題，是導數應用中的重要題型，在高考中多以壓軸題呈現，此類問題通常是通過對參數分類討論、求導、構造新函數、再求導等多步驟完成，過程之復雜令考生望而生畏，甚至直接舍棄第二問.對此，本文給出解決此類問題的一種方法，可以避免繁瑣的分類討論，對有些繁難的題目可以輕松破解.

此方法的思路是在審題中注意研究已知區間左端點的函數值或導函數值，并依據恒成立的不等式(或其變形)，構造一個必然成立的不等式，解此不等式得到參數的一個范圍(必要條件)；然后再證明該范圍(或該范圍內的一部分)是“不等式恒成立”的充分條件. 即從“不等式恒成立”的必要條件和充分條件兩個方面，求得參數的取值范圍.

【例1】(2016·臨沂11月質檢)已知函數f(x)=ln(x+1)-ax,a∈R.

(Ⅰ)求函數f(x)的單調區間；

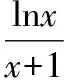
解：(Ⅰ)略；

(Ⅱ)當m≥0時，討論f(x)與g(x)的圖象的交點個數.

解：(Ⅰ)略.

① 因為g(1)=0，由g(x)≤0在[1,+∞)上恒成立，則必有g′(1)≤0.

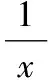
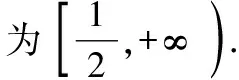
此解法由①②兩個方面構成，通過①由給定區間左端點的導函數值構造不等式g′(1)≤0，求得a的范圍，但此范圍是原不等式恒成立的必要條件；又通過步驟②證明此范圍是原不等式恒成立的充分條件.綜合①②知，所求a的范圍即是原不等式恒成立的充要條件，故而正確.

【例2】已知函數f(x)=alnx,a∈R.

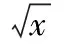
(Ⅱ)若對?x∈[1,e]，都有f(x)≥-x2+(a+2)x成立，求a的取值范圍.

解：(Ⅰ)略；

(Ⅱ)①令u(x)=f(x)+x2-(a+2)x=alnx+x2-(a+2)x，由題意，對?x∈[1,e]，u(x)≥0恒成立，則必有u(1)=1-(a+2)≥0，解得a≤-1.

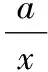
因為x∈[1,e]，所以x-1≥0，2x-a≥2x+1gt;0，所以u′(x)≥0，則u(x)在[1,e]上為單調增函數，則u(x)≥u(1)≥0，即原不等式成立.

綜上，實數a的取值范圍為a≤-1.

此解法是由給定區間左端點的函數值構造一個不等式，求得a的范圍，然后通過②證明此范圍是原不等式恒成立的充分條件.

【例3】已知函數f(x)=a2x3-3ax2+x+1，當x∈[1,+∞)時，f(x)gt;0，求實數a的取值范圍.

解：①令f(1)gt;0，得a2-3a+2gt;0，解得alt;1或agt;2.

②當a≤0時，由x∈[1,+∞)，易得f(x)=a2x3-3ax2+x+1gt;0，即當a≤0時，f(x)gt;0在x∈[1,+∞)上恒成立；

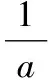
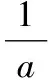
綜上，實數a的取值范圍是(-∞,0]∪(2,+∞).

本題同例2的方法先求得a的一個范圍，但需要對此范圍進行甄別，通過檢驗去除不合題意的部分，然后證明其余范圍是原不等式恒成立的充分條件.

【例4】(2015·山東理)設函數f(x)=ln(x+1)+a(x2-x)，其中a∈R.

(Ⅰ)討論函數f(x)極值點的個數，并說明理由；

(Ⅱ)若?xgt;0,f(x)≥0成立，求a的取值范圍.

解：(Ⅰ)略；

(Ⅱ)當a=0時，對?xgt;0,f(x)gt;0顯然成立；

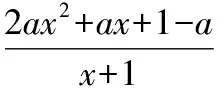
山東省臨沂市教育科學研究中心)