高考新熱點
——極值點偏移問題的通性通法

四川 肖 斌

高考新熱點
——極值點偏移問題的通性通法

四川 肖 斌

已知函數f(x)在定義域內有唯一的極值點x=x0，且x1,x2是f(x)的兩個零點(或滿足f(x1)=f(x2))，證明：x1+x2gt;(或lt;)2x0.

這便是近幾年數學高考和診斷考試中異常火爆的極值點偏移問題，本文試做系統探究.

一、極值點偏移的概念

1.極值點不偏移

2.極值點偏移

二、極值點偏移問題的通性通法

1.構造對稱型差函數

對于函數y=f(x)，若滿足f(a-x)=f(a+x)(或f(x)=f(2a-x))，則函數y=f(x)的圖象關于直線x=a對稱(即極值點不偏移).因此，要確定一個函數圖象不對稱(即極值點偏移)，只需考查f(a-x)與f(a+x)(或f(x)與f(2a-x))具有不等關系即可.因此，一個自然而然、卻極為重要的破解策略是構造基于對稱的差函數F(x)=f(x0+x)-f(x0-x)(或F(x)=f(x)-f(2x0-x)).

【例1】已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點.

(Ⅰ)求a的取值范圍；

(Ⅱ)設x1，x2是f(x)的兩個零點，證明：x1+x2lt;2.

【分析】

【解析】(Ⅰ)過程略.a的取值范圍為(0,+∞).

(Ⅱ)證明：f′(x)=(x-1)ex+2a(x-1)=(x-1)(ex+2a)，由(Ⅰ)知agt;0，f(x)在(-∞,1)上單調遞減，在(1,+∞)上單調遞增.

不妨設x1lt;x2，則有x1lt;1lt;x2，因為f(x1)=f(x2)=0，所以x1+x2lt;2?x1lt;2-x2lt;1?f(x1)gt;f(2-x2)?f(x2)gt;f(2-x2),

構造函數F(x)=f(x)-f(2-x)=(x-2)ex+a(x-1)2-[-xe2-x+a(1-x)2]=(x-2)ex+xe2-x,xgt;1，

則F′(x)=(x-1)(ex-e2-x)gt;0,所以函數F(x)在(1,+∞)上單調遞增，

所以F(x)gt;F(1)=0，即xgt;1時，f(x)gt;f(2-x).

因為x2gt;1,所以f(x2)gt;f(2-x2)，所以原不等式成立.

【感悟拓展】極值點偏移問題的證明步驟可歸納為“一求二差三判四脫”：

①求函數f(x)的極值點x0；

②構造差函數F(x)=f(x)-f(2x0-x)；

③判斷差函數F(x)的單調性，證明F(x)gt;(或lt;)0，即f(x)gt;(或lt;)f(2x0-x)；

④由x1,x2的范圍，結合f(x1)=f(x2)及原函數f(x)的單調性，“脫掉”f，確定x1+x2與2x0的大小關系.

口訣：極值偏離對稱軸，構造差函數覓行蹤；四個步驟環環扣，兩次單調性緊跟從.

【類題演練】(2016·蘭州市高三診斷)已知函數f(x)=ex-ax-1(a為常數)，曲線y=f(x)在與y軸的交點A處的切線斜率為-1.

(Ⅰ)求a的值及函數y=f(x)的單調區間；

(Ⅱ)若x1lt;ln2，x2gt;ln2，且f(x1)=f(x2)，試證明：x1+x2lt;2ln2.

【解析】(Ⅰ)過程略.a=2，y=f(x)的單調遞減區間為(-∞,ln2)，單調遞增區間為(ln2,+∞).

(Ⅱ)證明：由(Ⅰ)知f(x)=ex-2x-1，設xgt;ln2，所以2ln2-xlt;ln2，

所以g(x)在(ln2,+∞)上單調遞增，g(x)gt;g(ln2)=0，

即xgt;ln2時，f(x)gt;f(2ln2-x).

因為x1lt;ln2，x2gt;ln2，2ln2-x2lt;ln2，且f(x1)=f(x2)，

所以f(x1)=f(x2)gt;f(2ln2-x2)，即

f(x1)gt;f(2ln2-x2).

由(Ⅰ)知函數y=f(x)在(-∞,ln2)上單調遞減，

所以x1lt;2ln2-x2，所以x1+x2lt;2ln2.

2.將雙變量作差進行一元代換后構造新函數

在求解一類以指數型函數為背景的極值點偏移問題時，由于含有雙變量x1,x2，通常將雙變量作差進行一元代換后構造新函數，比如令t=x2-x1,轉化為單變量t的函數．

【例2】(2016·湖北省長沙市高三模擬試題節選)函數f(x)=ex-ax+a(a∈R)，其圖象與x軸交于A(x1,0),B(x2,0)兩點，且x1lt;x2.

(Ⅰ)求a的取值范圍；

【解析】(Ⅰ)f′(x)=ex-a，若a≤0，則f′(x)gt;0，則f(x)是單調增函數，這與題設矛盾，所以agt;0.當f′(x)lt;0時，xlt;lna，f(x)單調遞減；當f′(x)gt;0時，xgt;lna，f(x)單調遞增，故當x=lna時，f(x)取得極小值．

因為函數f(x)=ex-ax+a(a∈R)的圖象與x軸交于兩點A(x1,0),B(x2,0)，

所以f(lna)=a(2-lna)lt;0，即agt;e2，此時，存在1lt;lna，有f(1)=egt;0；存在3lnagt;lna，有f(3lna)=a3-3alna+agt;a3-3a2+agt;0，

又由f(x)在(-∞,lna)上單調遞減，在(lna,+∞)上單調遞增及曲線在R上不間斷，可知agt;e2為所求取值范圍．

(Ⅰ)若函數f(x)的圖象在x=0處的切線方程為y=2x+b，求a,b的值；

(Ⅱ)若函數f(x)在R上是增函數，求實數a的取值范圍；

【解析】(Ⅰ)過程略.a=-1,b=1.

(Ⅱ)由題意f′(x)≥0，即ex-x-a≥0恒成立，所以a≤ex-x恒成立．

設h(x)=ex-x，則h′(x)=ex-1．

x(-∞，0)0(0，+∞)h′(x)-0+h(x)減函數極小值增函數

所以h(x)min=h(0)=1，所以a≤1．

因為x1,x2是函數g(x)的兩個不同極值點，不妨設x1lt;x2，

所以agt;0且g′(x1)=0，g′(x2)=0．

(若a≤0，則g″(x)=ex-2agt;0，即g′(x)是R上的增函數，g′(x)=0至多有一個實根，與g(x)恰有兩個不同的極值點x1,x2矛盾)

所以ex1-2ax1-a=0，ex2-2ax2-a=0．

3.將雙變量作商進行一元代換后構造新函數

【例3】(2017·哈爾濱市高三模擬試題)已知函數f(x)=x2-(a-2)x-alnx.

(Ⅰ)判斷函數f(x)的單調性；

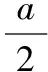
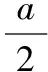
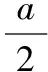
(Ⅰ)求f(x)的解析式并寫出定義域；

4.化歸為幾何—對數—算術平均值不等式模型

【例4】(2017·云南11校跨區調研試題改編)已知f(x)=lnx-ax有兩個零點x1,x2，

(Ⅰ)求實數a的取值范圍；

(Ⅱ)求證：x1·x2gt;e2.

(Ⅱ)證明：不妨設x1gt;x2gt;0,由已知得lnx1=ax1,lnx2=ax2,

相加得lnx1+lnx2=a(x1+x2),欲證x1x2gt;e2,只需證ln(x1x2)gt;2,

【類題演練】(2010·天津卷·理21題節選)已知函數f(x)=xe-x(x∈R)，如果x1≠x2，且f(x1)=f(x2)，證明：x1+x2gt;2.

證明：由f(x1)=f(x2)，得x1e-x1=x2e-x2，兩邊同時取以e為底的對數，

通法是熟練了的技巧，技巧是陌生的通法，當我們對一種解題技巧有刻骨銘心的感悟時，最易固化成我們心靈深處的通法.

本文概述的四種方法貌似不同，實則相通，文中的每一道題目幾乎都可用多法破解，這些策略已由生澀的技巧演進為必須熟練掌握的通性通法了.

四川省巴中中學)