解三角形的幾個技巧
2017-12-14 03:18:07山西李有貴
教學考試(高考數學) 2017年6期
山西 李有貴
解三角形的幾個技巧
山西 李有貴
解三角形問題的常規解法是利用正余弦定理,以及三角函數公式求解.孰不知勾股定理是余弦定理的特殊情形,銳角三角函數的定義方法是在直角三角形中定義的,因而解三角形的問題,可以通過作高得到直角三角形,利用三角函數的定義、勾股定理,以及特殊直角三角形來解題.
一、構造特殊直角三角形解題

【解析】如圖,作AE⊥BC于E,CF⊥AB于F.








由勾股定理得


所以∠BAC=60°.




二、利用三角函數的定義解題
【例2】已知在△ABC中,若C=120°,tanA=3tanB,sinA=msinB,則實數m=________.
【解析】如圖,

作AD⊥BC交BC延長線于D,設CD=1,




【評注】過A作三角形的高AD.由C=120°為特殊角,既可以利用特殊直角三角形中三邊之間的關系,又可以利用三角函數的定義得到tanA,tanB的表達式,因而可以利用方程求解.利用兩角和的正切公式求出x后,利用正弦定理求出m.


【簡解】如圖,作AD⊥BC于D,



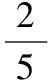
在△ABD中,

三、轉化為方程(組)解題




在△BCD,△ABD中,由勾股定理得
x2+h2=49②,y2+h2=64③,
③-②得y2-x2=15,即(y+x)(y-x)=15,
②+③-2×①得(y-x)2=9,即y-x=3.






【簡解】如圖,作平行四邊形BADC,

作CE⊥AB,DF⊥AB,垂足為E,F.
所以△BCE≌△ADF.


所以AF=BE=4x.在△BDF中,







四、構造相似三角形解題
【例4】已知△ABC,AB=AC=4,BC=2,點D為AB延長線上一點,BD=2,連接CD,則△BDC的面積是________,cos∠BDC=________.



【評注】求三角形面積最常用的公式是底與高的積的一半,求角的余弦值用三角函數定義求解.因而想到作AB邊上的高CE,BC邊上的高AF,利用等腰三角形性質,構造相似三角形求解.

山西省臨縣第一中學)
猜你喜歡
小學生學習指導(低年級)(2022年9期)2022-10-08 03:12:02
中學生數理化·中考版(2022年8期)2022-06-14 06:55:52
中等數學(2022年2期)2022-06-05 07:10:50
小學生學習指導(低年級)(2021年4期)2021-07-21 01:59:26
小學生學習指導(低年級)(2020年6期)2020-07-25 02:31:36
小學生學習指導(低年級)(2018年9期)2018-09-26 05:59:44
瘋狂英語·新讀寫(2018年2期)2018-09-07 09:32:10
中學生數理化·八年級數學人教版(2016年3期)2016-04-13 09:17:06
山東青年(2016年1期)2016-02-28 14:25:25
當代修辭學(2014年3期)2014-01-21 02:30:44

