一道高考題的解法與變式
山東 尹承利
一道高考題的解法與變式
山東 尹承利
高考試題大都具有典型性,既對知識與方法進行考查,又對思維縝密性進行考查,在我們教與學的過程中,重視對高考題潛在的知識、方法和應用價值進行挖掘,對于提高分析問題、解決問題的能力是頗為有益的.本文就2017年高考全國數學卷Ⅰ理科第10題(拋物線問題)的解法和變式進行探究,從而達到做一題會一類題、舉一反三、觸類旁通的效果.
一、試題呈現
例題(2017·全國卷Ⅰ理·10)已知F為拋物線C:y2=4x的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,|AB|+|DE|的最小值為
( )
A.16 B.14 C.12 D.10
二、解法分析
分析1.該題考查直線與拋物線(圓錐曲線)的位置關系,考查學生的分析問題解決問題的能力和數形結合的思想.在涉及直線與拋物線(圓錐曲線)的交點問題時,一般都設交點坐標為(x1,y1),(x2,y2),同時把直線方程與拋物線(圓錐曲線)方程聯立,消元后,可得x1+x2,x1x2,再把相關弦長用x1,x2表示出來,并代入剛才的x1+x2,x1x2,這種方法即解析幾何中的“設而不求”法,可減少計算量,簡化解題過程.
解法1.由題意易知直線l1,l2的斜率都存在且不為0.
設直線l1的方程為y=k(x-1)(不妨設kgt;0),

其判別式Δ=[-(2k2+4)]2-4k2·(-k2)=16(1+k2)gt;0.

所以由拋物線的定義得



設D(x3,y3),E(x4,y4),則x3+x4=2+4k2,
所以|DE|=x3+x4+p=2+4k2+2=4k2+4.


所以|AB|+|DE|取得最小值16.故選A.
點評:本解法取直線的斜率k為參數,設出直線方程并與拋物線方程聯立,運用“設而不求”、拋物線定義和均值不等式求解.“設而不求”是數學解題中的一種頗為有用的手段,往往能避免盲目推演而造成的無益的循環運算,從而達到準確、簡捷的解題效果.
分析2.由于數學中的定義是建構數學知識的基石,因而拋物線(圓錐曲線)的定義不僅是重要的知識點,也是解答許多數學問題的工具.在解答許多問題時,若能靈活、巧妙地應用拋物線(圓錐曲線)的定義,不僅能深化對拋物線(圓錐曲線)這一數學概念的深刻理解,而且還能提高學生應用定義去分析和解決問題的能力,開拓學生的思維視野.對于過拋物線(圓錐曲線)焦點的直線與拋物線的位置關系(即焦點弦問題)問題常利用拋物線的定義求解,回歸定義可使問題的解決變得簡單、方便.
解法2.如圖,

設AB傾斜角為θ.作AK1垂直準線,AK2垂直x軸.

所以|AF|·cosθ+p=|AF|.






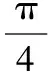
所以|AB|+|DE|的最小值為16.故選A.
點評:本解法取直線的傾斜角θ為參數,運用拋物線的定義、幾何關系轉化為角θ的正弦函數求解.
上述兩種方法是常規方法,需要同學們認真體會和熟練掌握.
通過該題,我們可以得到一般性的結論:已知F為拋物線C:y2=2px(pgt;0)的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,則|AB|+|DE|的最小值為8p.(證明仿照高考題的兩種解法即可)
三、試題變式

( )

分析:由例題的解法2可知




變式2.已知F為拋物線C:y2=4x的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,|AB|·|DE|的最小值為
( )
A.64 B.32 C.16 D.10

由該變式,我們可以得到一般性的結論:已知F為拋物線C:y2=2px(pgt;0)的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,則|AB|·|DE|的最小值為16p2.(證明仿照變式2的解法即可.)
變式3.已知F為拋物線C:y2=4x的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,四邊形ADBE面積的最小值為
( )
A.64 B.32 C.16 D.10
(1)對移動設備依賴加深。雖然利用碎片時間進行學習,但非教育類的各種類型的微信公眾平臺也層出不窮,學生在使用本微信公眾平臺時,有些自制能力差的可能被別的內容吸引,造成時間的浪費。解決這個問題的方法是一方面保證學習資源的質量,另一方面推送些時間管理、自律養成的網文。

由該變式,我們可以得到一般性的結論:已知F為拋物線C:y2=2px(pgt;0)的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,則四邊形ADBE面積的最小值為8p2.(證明仿照變式3的解法即可.)
變式4.已知F為拋物線C:y2=4x的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,線段AB的中點為M,線段DE的中點為N.
(Ⅰ)求△FMN面積的最小值;
(Ⅱ)求線段MN的中點P的軌跡方程.



(Ⅱ)設線段MN的中點P(x,y),

消去k后得y2=x-3.
故線段MN的中點P的軌跡方程為y2=x-3.
由該變式,我們可以得到一般性的結論:已知F為拋物線C:y2=2px(pgt;0)的焦點,過F作兩條互相垂直的直線l1,l2,直線l1與C交于A,B兩點,直線l2與C交于D,E兩點,線段AB的中點為M,線段DE的中點為N,則△FMN面積的最小值為p2.(證明仿照變式4(Ⅰ)的解法即可.)

山東省泰安英雄山中學)

