解題過程中挖掘“隱含信息”的幾種典型視角

四川 何志雄

解題過程中挖掘“隱含信息”的幾種典型視角

四川 何志雄

隱含信息是指題目中隱而未顯、含而未露同時需要不斷挖掘并利用條件進行推理和變形才能顯現出來的信息，它們常常巧妙地隱藏在題設背后，極易被忽略，但卻對揭示問題本質、實現解題突破、優化思維過程等起著關鍵作用，本文結合實例略談挖掘隱含信息的幾種常見視角，供大家參考．

一、挖掘定義的內涵

定義揭示了概念最本質的屬性，是研究概念的基礎和最有力的工具．挖掘定義的內涵實質上是為解題挖掘出最本質的條件，也是在為解題尋找一把鑰匙，讓解題過程更加簡捷明快，但只有在全面、深刻地理解定義的基礎上，才能從定義中挖掘出隱含信息，進一步指導解題．

【例1】 已知f(x)=ax2+bx+3a+b是偶函數，定義域為[a-1，2a]，則點(a，b)的軌跡是

( )

A．點 B．線段

C．直線 D．圓錐曲線

分析：本題常常會誤選成C，理由是因為f(x)是偶函數，于是得出一次項系數b=0，同時錯誤地以為a∈R．這樣的思路就恰好忽略了對奇(偶)函數定義的內涵的挖掘．

點評：挖掘定義的內涵解題不僅促進了對數學知識的融會貫通，而且比用其他方法更能顯得技高一籌，因此教學中應重視對這種無形知識的開發和利用．

二、挖掘局部與整體的內在聯系

對于題設出現較復雜的幾何體或代數式的情形，可將復雜的整體分解成若干個局部，然后對各個局部分別研究或著重研究某一特殊局部，接下來利用局部與整體的內在聯系，由局部推測或激活整體，以局部解決獲取整體解決．

( )

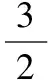
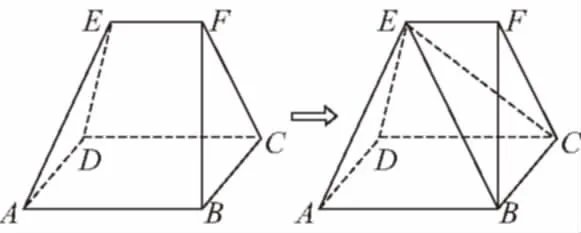
分析：本題的背景是非典型多面體，沒有現成的體積公式可用，可考慮對圖形進行分解，將其分割成特殊的幾何體，然后再挖掘局部與整體的內在聯系，使問題巧妙獲解.

解：直接計算該多面體的體積費時且比較困難，可連接BE,CE，則原多面體的體積轉化為四棱錐E-ABCD和三棱錐E-BCF的體積之和，易得四棱錐E-ABCD的體積VE-ABCD=6，由局部與整體的關系可知原多面體的體積應大于6，故選D.

【例3】 已知二次函數f(x)=ax2+bx(a,b為常數，a≠0)，f(2)=0，且方程f(x)=x有等根.

(Ⅰ)求f(x)的解析式；(Ⅱ)是否存在常數p，q(plt;q)，使f(x)的定義域和值域分別是[p，q]和[2p，2q]，如果存在，求出p，q的值；如果不存在，說明理由.

三、挖掘變元的取值范圍

這里所謂變元的取值范圍是指題設中并未給定，但卻隱藏在題中等式、不等式或圖形內的變元的取值范圍，挖掘出此類變元的取值范圍不僅是解題的必經之路，而且對于提高思維的嚴密性和敏捷度大有裨益.

分析：若直接判斷函數f(x)的奇偶性，則很難發現f(x)與f(-x)的關系，但若注意到函數的定義域，則絕對值符號就很容易去掉，問題的解決也就峰回路轉了.

【例5】 設α，β為銳角，且α+β=120°，試求函數y=cos2α+cos2β的最值．

點評：類似于本題，當題設中的某些條件是由多個變元組成的代數式時，各變元間往往不再具有獨立關系，而是一個變元的取值要受到另一個變元的制約或影響，此時應把其中一個變元用其他變元表示，并借助某些條件把其他變元的范圍求出來，這也是解決此類問題的關鍵一步.

四、挖掘代數關系的幾何背景

有些代數問題，若能根據已知代數關系的結構，挖掘出它的幾何背景，則可以通過化數為形，利用數學模型的直觀性，將抽象的數量關系轉化為具體的圖形，從而使問題巧妙地得到解決.

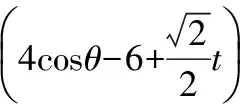
分析：本題表面上是一個關于t的二次式，但又有三角函數作另外的約束條件，因此從純代數角度采用常規思路難以解決.仔細觀察目標式后，不難挖掘出這樣的隱含信息：目標式的結構類似于兩點間的距離公式，于是可考慮從幾何角度解決問題.

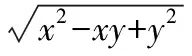
分析：仔細研究目標不等式，不難挖掘出這樣的隱含信息：目標不等式中的三個根號的值均大于0，該不等式的結構類似于“三角形中兩邊之和大于第三邊”，因此可考慮從幾何角度解決問題.

點評：在解決代數問題時，揭示出隱含在內部的幾何背景，不僅使抽象問題直觀化，復雜問題簡單化，獲得了避繁就簡、化難為易的新穎解法，而且對創造型思維的開發和培養也很有益處.

五、挖掘所給圖形是否經過特殊位置

在題設所給的圖形中，對尚未直接顯現出來的各個元素，通過合情的推理運算或添加適當的輔助線，將圖形所經過的特殊位置揭示出來，并充分發揮這些位置的作用，可以達到化難為易、迅速導出結論的目的.

( )

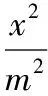
A.0 B.1

C.2 D.不能確定

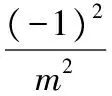
【例9】 已知A和B為拋物線y2=4px(pgt;0)上除原點以外的兩個動點，若OA⊥OB，OM⊥AB，求點M的軌跡方程，并說明它表示什么曲線.

點評：能否順利挖掘出圖形經過特殊位置的關鍵在于平時多進行這方面的思維訓練和總結歸納.

六、挖掘常見幾何圖形的固有屬性

研究幾何問題時，挖掘幾何圖形的固有屬性常常是必不可少的一環.若能充分挖掘出圖形的固有屬性，則往往會使代數運算大為簡化，使問題簡單明了，有時也可以用挖掘出的屬性繞開計算的暗礁，達到事半功倍的效果.

【例10】 已知點A(a，b)是圓D：x2+y2-2dx-2ey+f=0內的一定點，弦BC與點A組成一個直角三角形，且∠BAC=90°，求弦BC中點P的軌跡方程.

分析：要解決本題，不妨作出一個能大致反映題設的草圖，然后聯想到有“直角三角形中斜邊上的中線等于斜邊的一半”這樣的幾何屬性，若能及時挖掘出這樣的隱含信息，問題也就迎刃而解了.

四川省資陽市雁江區教育教學研究室)