巧借曲線切線,妙解五類問題
廣東 劉光明
巧借曲線切線,妙解五類問題
廣東 劉光明
曲線切線問題不僅僅是導數的幾何意義那么簡單,仔細琢磨推敲,曲線的切線可以從導數的幾何意義、恰到好處證明不等式、求參數范圍、含參函數的零點問題、曲線上點到直線的最短距離等角度進行考查,本文就此以例題分別展開闡述,期望從中以窺曲線切線的分析策略.
一、直接利用導數的幾何意義
【例題1】已知函數f(x)=2x3-3x,若過點P(1,t)存在三條直線與曲線y=f(x)相切,求實數t的取值范圍.

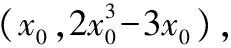
【評注】與曲線的切線有關的問題,主要從三個方面著手,一是曲線的切點,借助導數的幾何意義求出切線斜率;二是切點在曲線上;三是切點在切線上.無論含參與否,都緊抓以上三個方面聯立方程或者轉化為熟悉的知識點處理即可.
二、巧借曲線的切線化曲為直,化解計算尷尬,證明不等式
【例題2】已知函數f(x)=aex+(2-e)x(a為實數,e為自然對數的底數),曲線y=f(x)在x=0處的切線與直線(3-e)x-y+10=0平行.
(Ⅰ)求實數a的值,并判斷函數f(x)在區間[0,+∞)上的零點個數;
(Ⅱ)證明:當xgt;0時,f(x)-1gt;xln(x+1).
【簡解】(Ⅰ)a=1,函數f(x)在區間[0,+∞)上沒有零點(過程詳解略).
(Ⅱ)證明:不妨先證明當xgt;0時,f(x)-1≥x·x成立.
設g(x)=ex+(2-e)x-1-x2(xgt;0),則g′(x)=ex-2x+2-e,設φ(x)=ex-2x+2-e,
所以?x0∈(0,1),使得φ(x0)=0,故x∈(0,x0)∪(1,+∞)時,φ(x)gt;0,即g′(x)gt;0,x∈(x0,1)時,g′(x)lt;0,因此,函數g(x)在區間(x0,1)上單調遞減,在區間(0,x0)和(1,+∞)上單調遞增,且g(0)=g(1)=0,所以g(x)≥0(xgt;0),當且僅當x=1時等號成立,可得f(x)-1≥x·xgt;xln(x+1),故f(x)-1gt;xln(x+1).
【變式練習題1】(2015·山東卷理·21題節選改編)設函數f(x)=ln(x+1)+a(x2-x),當alt;0時,?x0∈(0,+∞)使得f(x0)lt;0.
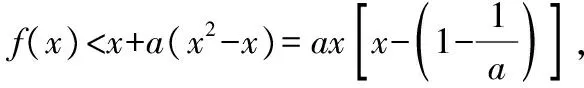
【評注】構造函數證明不等式中,若多次求導后均未能實現單調性或最值的求解,那么需要考慮放縮.中學階段的曲線切線,加上函數的凹凸性,恰好是一種極好的放縮.人教A版教材選修2-2第32頁習題1.3B組第1題中的不等式exgt;xgt;lnx提供了一個不錯的放縮思路.故平時多積累一些放縮的例子,為以后的不等式證明提供快捷思路.
三、巧借過定點切線,指引討論參數的方向
【例題3】已知函數f(x)=x+xlnx,若k∈Z,且k(x-1)lt;f(x)對任意xgt;1恒成立,求k的最大值.


【評注】通過曲線的切線去探求參數的范圍,主要還是利用導數求單調性、極值、邊界變化情況(變化趨勢),考慮函數的凹凸性,然后描繪曲線的大致圖象,數形結合,進而得到參數范圍.不過,借切線為邊界,只是探求參數的范圍,解決小題可以,但解答題需慎用.

( )
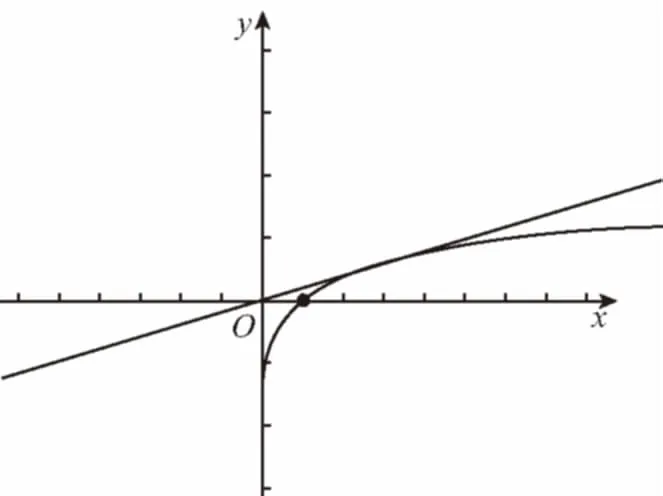

四、借用兩曲線的公切線,突破含參函數零點的討論



【評注】兩條曲線相切,其關鍵點是兩曲線在相切處導數值相等、函數值也相等.
五、妙用切線為橋梁,轉換思想求距離

【簡解】由直線的方程與橢圓的方程可以知道,直線l與橢圓不相交,設直線m平行于直線l,則直線m的方程可以寫成4x-5y+k=0,

令方程(*)中的判別式Δ=64k2-4×25(k2-225)=0,解得k1=25,k2=-25.
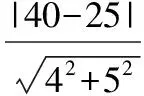

( )


【評注】由例題5和變式練習題3可知,對于求解曲線上一點到直線的最短距離問題,如果僅僅是利用導數處理最值,可能會遇到計算困難.巧妙借助切線,從幾何和代數相結合的角度,避免繁雜計算,自然轉化成點到直線距離問題,易懂易操作.特別是兩條不相交曲線間的最短距離,首先應該關注兩曲線是否對稱,借助對稱軸橋梁,處理距離最值.

廣東省華南師范大學附屬中學汕尾學校)

