幾何題組訓練
——立體幾何的計算

四川 陳曉芳

廣東 卜大海

遼寧 李海武

江蘇 王懷學

幾何題組訓練
——立體幾何的計算

四川 陳曉芳

廣東 卜大海

遼寧 李海武

江蘇 王懷學

1 公式法求幾何體的體積和表面積

1.1幾何體的側面積與表面積

【典例1】(1)若一個圓錐的側面展開圖是一個半徑為3 cm,圓心角為60°的扇形，則該圓錐的側面積和體積分別為________.

【解析】(1)如圖，PA=3 cm,∠BPA=60°，設OA=r，

所以，該圓錐的體積為

【變式1】一個高為2的圓柱，底面周長為2π，該圓柱的表面積為________．

【變式2】邊長為1的正方形的一邊所在直線為旋轉軸，將該正方形旋轉一周所得圓柱的側面積等于

( )

A．2π B．π C．2 D．1

【變式3】用一張4 cm×8 cm的矩形硬紙卷成圓柱的側面，則軸截面的面積為________(接頭忽略不計).

( )

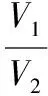
【解析】(1)在正△ABC中，D為BC中點，

因為平面BB1C1C⊥平面ABC,

AD⊥BC,AD?平面ABC,

所以AD⊥平面BB1C1C,

即AD為三棱錐A-B1DC1底面上的高.

故選C.

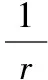
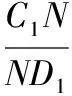
【變式4】Rt△ABC的邊長分別是3,4,5，現以斜邊AB所在的直線為軸把△ABC(及其內部)旋轉一周后，所得幾何體的體積是________ ．

1.2 “選準底面，找對高”

【典例】如圖所示，在邊長為4的正方形紙片ABCD中，AC與BD相交于O，剪去△AOB，將剩余部分沿OC，OD折疊，使OA，OB重合.

(1)以A，B，C，D，O為頂點的四面體O-ACD是怎樣的四面體？

(2)求證：OA⊥CD;

(3)求四面體的體積．

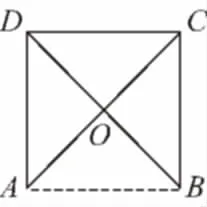
【解析】(1)折疊后的四面體如圖所示．OA,OC,OD兩兩相互垂直，即側棱兩兩垂直的三棱錐；

(2)證明:

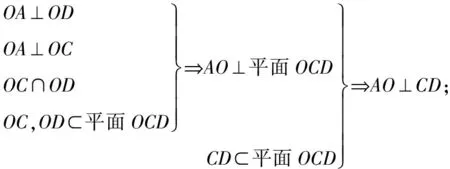
【變式1】如圖所示，在邊長為4的正方形紙片ABCD中，E，F分別為邊BC，CD的中點.

(1)沿圖中虛線折起，使得B，C，D三點重合，此時4個面圍成怎樣的幾何體？

(2)求圍成的幾何體的體積.

【變式2】如圖所示，在邊長為4的正方形紙片ABCD中，AC與BD相交于O,剪去△AOB,將剩余部分沿OC，OD折疊，使OA，OB重合，則以A(B)，C，D，O為頂點的四面體的體積為________.

【變式3】如圖，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC，AC=BC=CC1=2，AC⊥BC，點D是AB的中點,求四面體B1C1CD的體積．

1.3認清幾何體中的相關元素

【典例】在直棱柱ABC-A1B1C1中，AB⊥BC,BN⊥CB1,M∈AB.

求證：B1C⊥平面BNM.

【證明】在直棱柱ABC-A1B1C1中，B1B⊥平面ABC，

且AB?平面ABC,所以B1B⊥AB.

又AB⊥BC，B1B∩BC=B,B1B,BC?平面B1BC,

所以AB⊥平面B1BC,

因為B1C?平面B1BC,

所以AB⊥B1C，即MB⊥B1C,

因為MB⊥B1C，NB⊥B1C，MB∩BN=B,

MB,BN?平面BNG.

所以B1C⊥平面BNM.

【變式2】一個直角梯形的兩底長分別為2和5，高為4，繞其較長的底旋轉一周，所得到的幾何體的表面積為________.

1.4用直截面法求幾何體的體積

【典例】四面體的六條棱中，有五條棱長都等于a，則該四面體的體積的最大值為________.

【解析】如圖，在四面體ABCD中，

設AB=BC=CD=AC=BD=a，AD=x，

取AD的中點為P，BC的中點為E，連接BP,EP,CP．

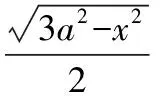
所以VA-BCD=VA-BPC+VD-BPC

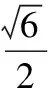
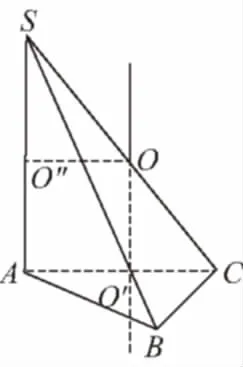
【變式1】已知球的直徑SC=4，A,B是該球球面上的兩點，AB=2，∠ASC=∠BSC=45°，則棱錐S-ABC的體積為

( )

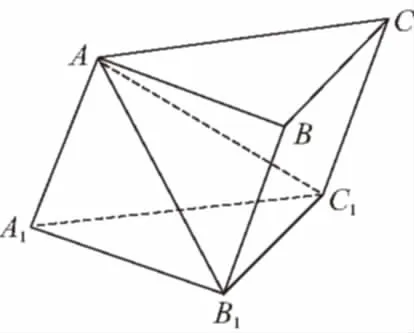
【變式2】如圖，在三棱柱ABC-A1B1C1中，側棱AA1⊥平面AB1C1，AA1=1，底面△ABC是邊長為2的正三角形，求此三棱柱的體積.

1.5用等體積法求體積

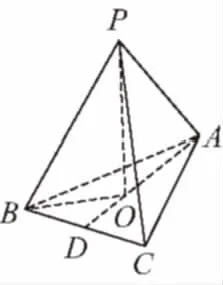
【典例1】將邊長為1的正方形ABCD沿對角線AC折起，使△ABD為正三角形，則三棱錐A-BCD的體積為

( )

【解析】如圖，取AC的中點O,連接BO,DO,

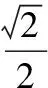
因為△ABD為正三角形,DB=1,DO2+BO2=DB2,

所以DO⊥OB,所以DO⊥平面ABC,

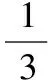
故選D.

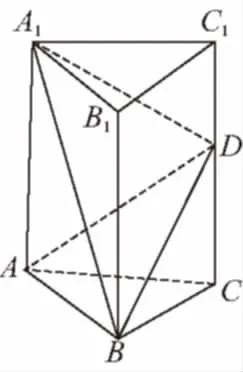
【變式1】如圖，直三棱柱ABC-A1B1C1中，各側棱和底面的邊長均為a，點D是CC1上任意一點，連接A1B,BD,A1D,AD，則三棱錐A-A1BD的體積為________．

【變式2】如圖，四棱錐P-ABCD中，PA⊥底面ABCD，底面ABCD是矩形，AB=2,AD=3,PA=4，點E為棱CD上一點，則三棱錐E-PAB的體積為________．

【變式3】如圖，在長方體ABCD-A1B1C1D1中，AB=BC=1，AA1=2，E是側棱BB1的中點．

(1)求證：A1E⊥平面ADE；

(2)求三棱錐A1-ADE的體積．

【典例2】如圖，正方體ABCD-A1B1C1D1的棱長為1，E，F分別為線段AA1，B1C上的點，則三棱錐D1-EDF的體積為________．

【解析】(法1)三棱錐D1-EDF的體積即為三棱錐F-DD1E的體積．

因為E，F分別為AA1，B1C上的點，

所以在正方體ABCD-A1B1C1D1中，

(法2)將E點平移到A點，將F點平移到C點，

( )

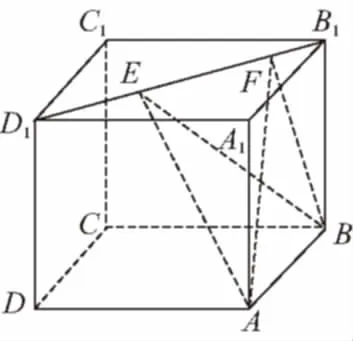
A.AC⊥BE

B.EF∥平面ABCD

C.三棱錐A-BEF的體積為定值

D.△AEF的面積與△BEF的面積相等

【變式3】如圖，在棱長為1的正方體ABCD-A1B1C1D1中,E是棱BC上的一點，則三棱錐D1-B1C1E的體積為________.

2 球的相關計算

2.1球的截面的性質

①弦AB，CD可能相交于點M；

②弦AB，CD可能相交于點N；

③MN的最大值為5；

④MN的最小值為1.其中真命題的個數為

( )

A.1個 B.2個

C.3個 D.4個

【解析】當弦AB，CD相交時，則在一個截面圓上，由于ABlt;CD，所以弦AB，CD可能相交于點M，弦AB，CD不可能相交于點N.故①是真命題；②是假命題；

連接OM，ON，當OMN為三角形時，由于OM+ONgt;MN，OM-ONlt;MN，所以，當MN共線且在球心O的不同側時，MN取得最大值5；當MN共線且在球心O的同側時，MN取得最小值1.故③④為真命題.

【變式1】已知過球面上三點A，B，C的截面和球心的距離等于球半徑的一半，且AB=BC=CA=1，則該球的半徑是

( )

【變式2】用與球心距離為1的平面去截球，所得的截面面積為π，則球的體積為

( )

【變式3】過球的一條半徑的中點，作垂直于該半徑的平面，則所得截面的面積與球的表面積的比為

( )

( )

【變式5】一個與球心距離為1的平面截球所得的圓面面積為π，則球的表面積為________．

2.2將三棱錐補形成長方體求外接球的半徑

【解析】如圖，將正三棱錐補形成正方體，可知球心O為體對角線PD的中點，

設P到平面ABC的距離為h，

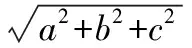
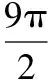
【變式2】正四面體的四個頂點都在同一個球面上，且正四面體的高為4，則這個球的表面積是________．

【變式3】如圖，在三棱錐V-ABC中，VA⊥底面ABC,∠ABC=90°,若VA=1,AB=2,BC=3，則三棱錐外接球的表面積為________．

2.3確定球心的位置

【評注】當球面上有四點P，A，B，C滿足PA，PB，PC兩兩互相垂直時，正三棱錐P-ABC的外接球就是以PA，PB，PC為棱的正方體的外接球，球心在其體對角線的中點處．

從局部看，簡單幾何體的頂點到其外接球球心的距離是相等的，可以先考慮到一個平面上的點(三個或三個以上)等距離的點的集合，因此可以借助勾股定理、垂徑定理、射影定理等計算圓心位置．

( )

【變式2】如圖，三棱錐S-ABC中，SA⊥平面ABC，SA=2，△ABC是邊長為1的正三角形，則其外接球的體積是________.

【變式4】某球的外切圓臺上下底面半徑分別為r,R，求該球的體積________.

3 簡單幾何體中的最值問題

3.1利用運動變化的觀點求解幾何體的最值

【典例】已知在半徑為2的球面上有A,B,C,D四點，若AB=CD=2，則四面體ABCD的體積的最大值為________．

【解析】如圖，過CD作平面ECD，

使AB⊥平面ECD，交AB于E，

設點E到CD的距離EF=d，

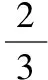
當球的直徑通過AB與CD的中點時，

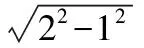
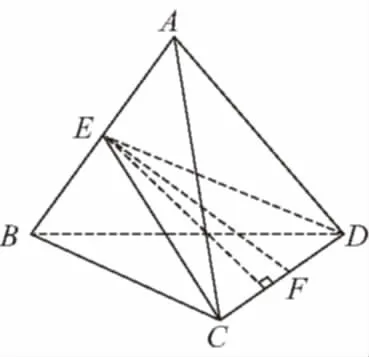
【變式1】三棱錐A-BCD中，AB=BC=CA=BD=CD=1，則該三棱錐體積的最大值為________．

【變式3】在封閉的直三棱柱ABC-A1B1C1內有一個體積為V的球，若AB⊥BC,AB=6,BC=8,AA1=3,則V的最大值是

( )

3.2利用側面展開圖“化曲為直”求距離的最值

【典例1】如圖，已知圓錐的底面半徑為1，母線SA長為6，M為SA的中點，有一根繩子從A點出發，沿圓錐的側面繞一周到達M點，問繩子最短是多少？

【解析】沿母線SA將圓錐側面展開，

AM點分別對應展開圖中的A1，M1點，

則在展開圖中，線段AM1的長度即為最短繩長.

所以△SA1A是正三角形，

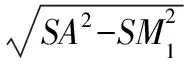
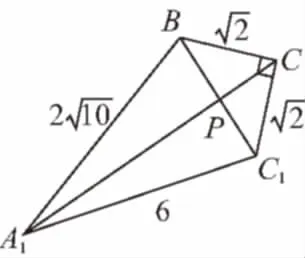
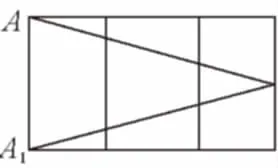
【變式3】如圖，已知正三棱柱ABC-A1B1C1的底面邊長為1，高為8，一質點自A點出發，沿著三棱柱的側面繞行兩周到達A1點的最短路線的長為________．

3.3利用基本不等式求體積的最值

【典例】(1)已知正六棱柱的12個頂點都在一個半徑為3的球面上，當正六棱柱的體積最大(柱體體積=底面積×高)時，其高的值為________.

(2)一個圓柱體的體積是16 πcm,求其表面積的最大值.

【解析】(1)設正六棱柱的底面邊長為a，高為2h，

則a2+h2=9，

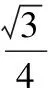
(2)設圓柱體的高為h，底面半徑是r，16π=πr2h，

圓柱體的表面積

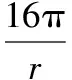
圓柱體的表面積Smax=24π.

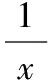
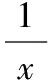
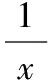
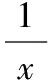
3.4利用導數求體積的最值

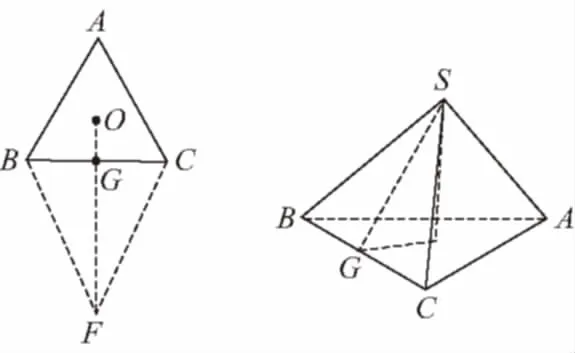
【典例1】某商場為促銷要準備一些正三棱錐形狀的裝飾品，用半徑為10 cm的圓形包裝紙包裝．要求如下：正三棱錐的底面中心與包裝紙的圓心重合，包裝紙不能裁剪，沿底邊向上翻折，其邊緣恰好達到三棱錐的頂點，如圖所示．設正三棱錐的底面邊長為xcm，體積為Vcm3．在所有能用這種包裝紙包裝的正三棱錐裝飾品中，V的最大值是多少？并求此時x的值．

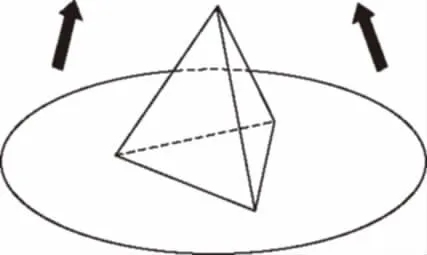
【解析】正三棱錐展開如圖所示．當按照底邊包裝時體積最大．

設正三棱錐側面的高為h0，高為h．

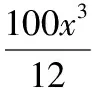
【變式1】設正四棱錐的側棱長為1，則其體積的最大值為________．

【變式2】有一個各條棱長均為a的正四棱錐，現用一張正方形包裝紙將其完全包住，不能剪裁，但可以折疊，則包裝紙的最小邊長是________．

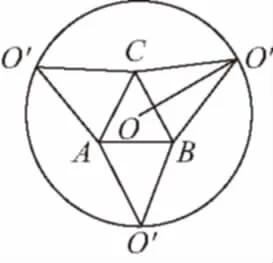
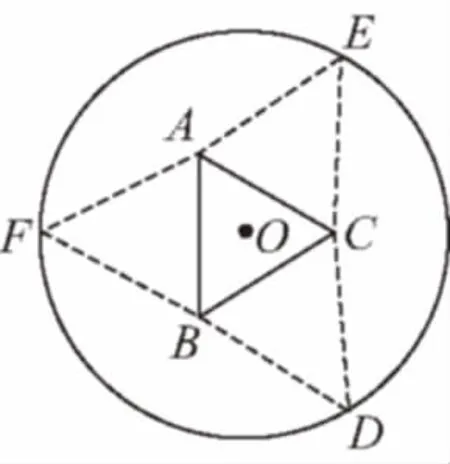
【變式3】如圖，圓形紙片的圓心為O，半徑為5 cm，該紙片上的等邊三角形ABC的中心為O.D，E，F為圓O上的點，△DBC，△ECA，△FAB分別是以BC，CA，AB為底邊的等腰三角形.沿虛線剪開后，分別以BC，CA，AB為折痕折起△DBC，△ECA，△FAB，使得D，E，F重合，得到三棱錐.當△ABC的邊長變化時，所得三棱錐體積(單位：cm3)的最大值為________.

3.5構造二次函數求最值

【典例】如圖所示，為了制作一個圓柱形燈籠，先要制作4個全等的矩形骨架，總計耗用9.6米鐵絲，再用S平方米塑料片制成圓柱的側面和下底面(不安裝上底面).當圓柱底面半徑r取何值時，S取得最大值？并求出該最大值(結果精確到0.01平方米).

【解析】設圓柱形燈籠的母線長為l，則8l+16r=9.6，

解得l=1.2-2r(0lt;rlt;0.6)，

則S=2πrl+πr2=2πr(1.2-2r)+πr2=-3π·(r-0.4)2+0.48π，

當r=0.4時，S=0.48π≈1.51，S取得最大值約為1.51平方米.

【評注】在求表面積或體積的最值時，常常將目標表示為某個量(半徑或高等)的二次函數，然后用配方法尋求最值(注意標出定義域).

【變式1】已知圓錐的底面半徑為R，高為3R，在它的所有內接圓柱中，全面積的最大值是________．

【變式2】已知圓錐的底面半徑為R，高為3R，在它的所有內接圓柱中，側面積的最大值是________．

3.6構造三角函數求最值

【典例】如圖，半徑為R的球O中有一內接圓柱．當圓柱的側面積最大時，球的表面積與圓柱的側面積之差是________．

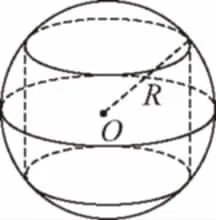
【解析】如圖，設球的一條半徑與圓柱相應的母線夾角為α，

則圓柱的側面積S=2π·Rsinα·2Rcosα=2πR2sin2α，

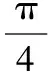
此時球的表面積與該圓柱的側面積之差為2πR2．

【評注】在球的相關截面中，我們常常將從球心引出的角度設為參量α，將目標量表示為參量α的三角函數，然后由正弦值或余弦值的有界性[-1,1]，得出目標函數的最值.

【變式1】點P在直徑為2的球面上，過P作兩兩垂直的三條弦，若其中一條弦長是另一條弦長的2倍，則這三條弦長之和為最大值是________．

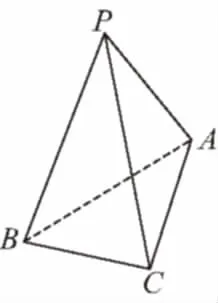
【變式2】如圖所示，三棱錐P-ABC的底面ABC為等腰三角形，AB=AC=a，側棱長均為2a，問BC為何值時，三棱錐P-ABC的體積V最大，最大值是多少？

參考答案

1 公式法求幾何體的體積和表面積

1.1幾何體的側面積與表面積

【典例1】1.6π 【解析】底面圓的周長2πr=2π，所以圓柱的底面半徑r=1，所以圓柱的側面積為4π，兩個底面積為2πr2=2π，所以圓柱的表面積為6π.

2.A 【解析】以正方形的一邊所在直線為軸旋轉得到的圓柱底面半徑r=1，高h=1，所以側面積S=2πrh=2π.故選A.

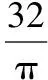
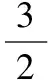
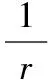
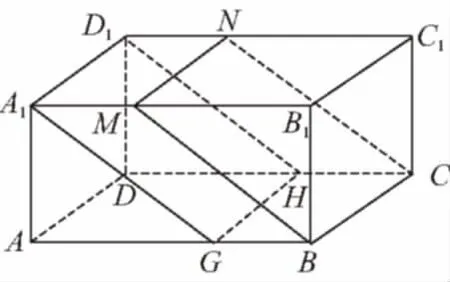
3.2 【解析】將該長方體站立放置，分別是直三棱柱、直四棱柱、直三棱柱．VAA1G-DHD1=VA1GBM-D1HCN=VMBB1-NCC1,由于它們等高，因此底面積也應該相等，也就是說SRt△A1AG=S=SRt△BB1M，即AG×h=GB×h，所以AG=2GB．所以=2.

1.2“選準底面，找對高”

【典例】

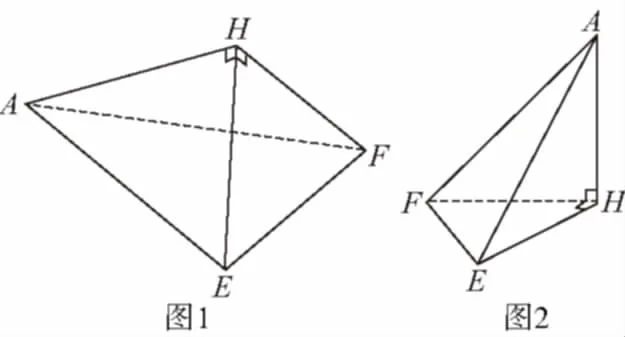
1.【解析】(1)4個面圍成幾何體是一個三棱錐，它的底面是AEF，B,C,D三點重合于一點，設為點H，側棱AH，HE，HF兩兩垂直，如圖1.

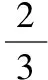
1.3認清幾何體中的相關元素

1.4用直截面法求幾何體的體積

1.5用等體積法求體積

【典例1】

3.【解析】(1)證明：由勾股定理知，

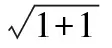
則A1A2=A1E2+AE2，

所以A1E⊥AE.

因為AD⊥平面AA1B1B，A1E?平面AA1B1B，

所以A1E⊥AD，

而AD∩AE=A，所以A1E⊥平面ADE.

【典例2】

1.D 【解析】連接BD，AC，因為AC⊥BD,AC⊥DD1,BD∩DD1=D,則AC⊥平面BB1D1D，BE?平面BB1D1D，所以AC⊥BE,A正確；BD∥B1D1，EF∥平面ABCD正確；又因為△BEF面積是定值，AC⊥平面BB1D1D，三棱錐A-BEF的高即為A到平面BB1D1D的距離，所以三棱錐A-BEF的體積是定值，從而A，B，C正確.因為點A，B到直線B1D1的距離不相等，所以△AEF的面積與△BEF的面積不相等，D錯誤.故選D.

2.球的相關計算

2.1球的截面的性質

【典例1】

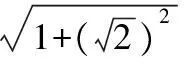
2.2將三棱錐補形成長方體求外接球的半徑

2.3確定球心的位置

3簡單幾何體中的最值問題

3.1利用運動變化的觀點求解幾何體的最值

【典例1】

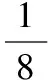
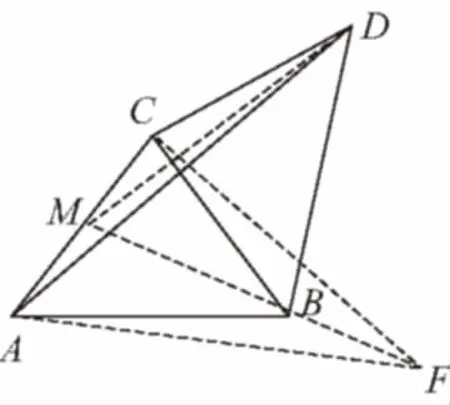
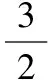
3.2利用側面展開圖“化曲為直”求距離的最值

3.3利用基本不等式求體積的最值

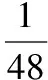
3.4利用導數求體積的最值

【典例1】

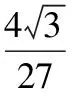
3.5構造二次函數求最值

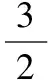
3.6構造三角函數求最值