片狀體最小懸浮速度的計算模型

袁成宇，王 娟，陳致水，廖宇蘭

(海南大學 機電工程學院，海口 570228)

?

片狀體最小懸浮速度的計算模型

袁成宇，王 娟，陳致水，廖宇蘭

(海南大學 機電工程學院，海口 570228)

片狀體最小懸浮速度可通過傳統理論計算和試驗獲取，因此提出了一種處于壓差阻力狀態下的片狀體最小懸浮速度的計算模型。同時，以甘蔗葉為對象，通過自制的懸浮速度測試裝置進行了測試。通過比較發現：傳統理論計算的蔗葉最小懸浮速度與實測的最小懸浮速度相差較大，最大相對誤差為97.3%，最小相對誤差為39.4%；而采用本文提供的方法所得的計算結果與實測值的最大相對誤差為24.9%，最小相對誤差為4.75%。

片狀物；最小懸浮速度；數學模型

0 引言

物料懸浮速度是指在垂直氣流的作用下，物料所受氣流作用力等于該物料本身的重力，而使其保持平衡狀態時的氣流速度，它是進行風選除雜及確定物料氣力輸送運動的主要依據。目前，獲取物料懸浮速度的方法主要有理論計算與實驗測量兩種。對于比較規則的球體或類似球體物料，一般通過理論計算可以獲得比較合理的結果；而對于與球體偏差較大或者不規則物料，一般通過體積當量球等理論可計算得出相應的懸浮速度。例如，須山啟介等對谷粒在垂直氣流中的懸浮速度，李學軍等對茶葉的懸浮速度及在空氣中的運動、周作伸等對羽毛在空氣中的運動，干方建等對煙草在氣流中的懸浮運動進行了理論分析，得出了相應的計算結果，但在分析過程中采用了近似處理，其結果可能與實際情況產生一定偏差，最終仍需通過試驗方法加以修正。本文根據片狀顆粒在垂直流場中的受力分析，給出了一種相對簡單的懸浮速度計算模型，并通過自制的測試裝置驗證該模型計算結果與不規則片狀體傳統理論計算的懸浮速度的一致程度。

1 懸浮速度傳統計算方法

目前，懸浮速度一般是根據物料在流場中的受力平衡進行計算的，即物料重力等于流動阻力和浮力之和。傳統方法計算的公式表達為

(1)

其中，v為顆粒最小懸浮速度(m/s)；ρs為懸浮顆粒密度(kg/m3)；ρg為氣流密度(kg/m3)；d為顆粒直徑(m)；C為阻力系數；g為重力加速度(9.81N/kg)。當不規則顆粒處于壓差阻力區時，C為常數取0.44，顆粒直徑以體積當量直徑代替，此時懸浮速度的計算公式為

(2)

其中，de為等體積當量直徑，de=1.24(m/ρs)1/3，m為顆粒質量；K為形狀影響系數。利用公式(2)可求出的顆粒的懸浮速度，但對片狀體而言，由于其形狀與球體存在很大差異，即使通過形狀影響系數修正，其計算結果也可能存在較大偏差。

2 片狀體最小懸浮速度計算模型

設有一均質片狀顆粒在流速為u流場中的壓差阻力區處于懸浮狀態，其受力分析如圖1所示。

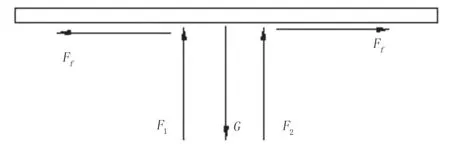
圖1 葉片懸浮態受力分析

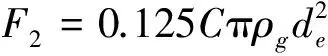
G=F1+F2

(3)

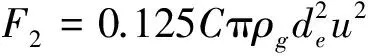
(4)

由貝努力方程可近似認為風速與風動壓的關系為

(5)

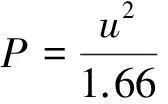
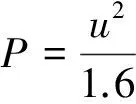
(6)

整理可得片狀顆粒懸浮速度的公式為

(7 )

當懸浮片狀物的密度ρs?ρg時，則式(7)可以簡化為

(8)

式(8)即為片狀體最小懸浮速度計算的數學模型。其中，V為片狀體的體積(m3)；S為迎流面積(m2)；ρs為懸浮顆粒密度(kg/m3)；m為質量(kg)。從公式(8)可知：片狀體的最小懸浮速度不需要考慮體積當量直徑和形狀系數的影響，當均質片狀體迎風面積相同時，最小懸浮速度僅與質量m有關。

3 試驗驗證

為驗證公式(8)的合理性，通過自制的懸浮速度測量裝置對一定幾何尺寸的甘蔗葉的最小懸浮速度進行了試驗驗證。

3.1 試驗裝置與測量儀器

自制的試驗測量裝置見圖2所示。其中，D為調節風機轉速的變頻器，其調節范圍為0～50Hz；風速儀為testo405-V1手持式測速儀，其測量范圍為0～20m/s，精度為0.01m/s；稱重計最大量程為10kg，精度為0.1g；蔗葉的幾何尺寸采用游標卡尺測量。

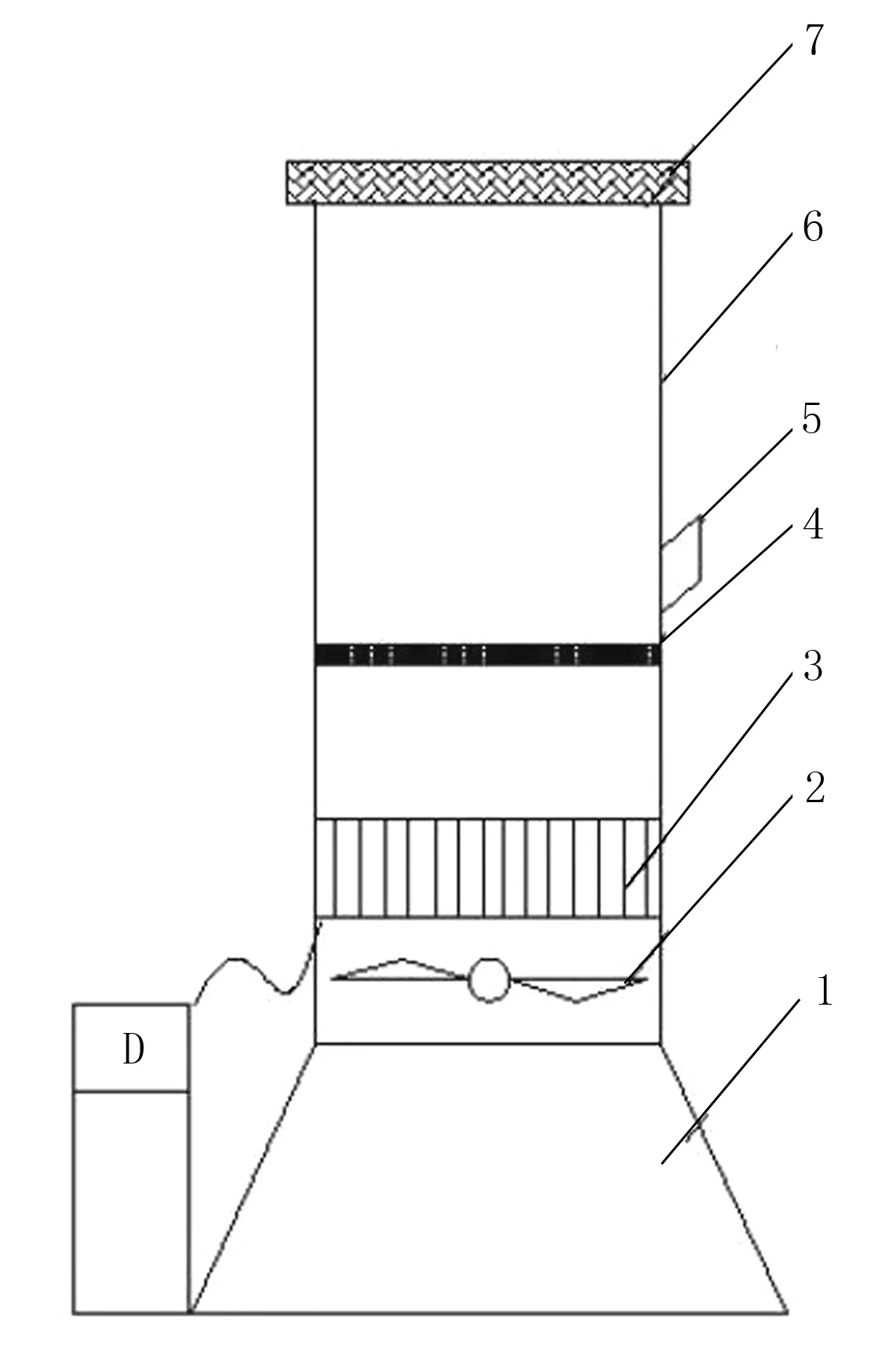
圖2 懸浮速度測量裝置

3.2 試驗材料

試驗樣品為成熟甘蔗上采取的甘蔗青葉中間段，取自學校某試驗基地，其含水率處于71.01%～73.14%，平均寬度處于3.1～4.2cm之間。表1為試驗樣品的其他基本參數。

表1 試驗樣品參數

3.3 測試裝置精度驗證

由于是自制懸浮速度裝置，先需要驗證測試裝置是否滿足懸浮速度的測試要求。驗證采用的方法為：對物料網上方的玻璃圓管徑向截取5個等距截面，每個截面按等面積同心圓環原理選取7個測點，設測點從左至右為測點1～測點7。當變頻器示數為45Hz時，各個截面上風速的測量結果如表2所示。

表2 截面上風速測量結果(變頻器讀數為45Hz)

從表2中測量數據可知:試驗裝置可滿足懸浮速度試驗的測量要求。

3.4 測量方法

首先將樣品置于物料網中央，調節變頻器，使蔗葉段在氣流作用下上升進入測量段并保持其懸浮，通過玻璃圓管邊上的標尺記下此時蔗葉上升的高度和變頻器的讀數；取出樣品后，再將變頻器調至相同的讀數，測量標記位置所處截面風速即為最小懸浮速度。每一樣品在同一條件下測量3次，取3次平均值作為蔗葉的最小懸浮速度。

3.5 測量結果

將測量所得結果與傳統懸浮速度計算方法和本文提供的計算方法所得結果相比較，如圖3所示。

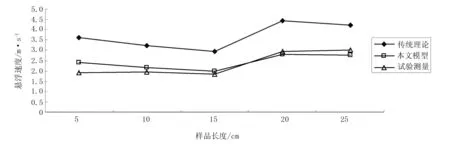
圖3 3種方式所得結果比較圖

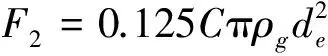
4 結論

通過分析片狀體在垂直流場中的受力，建立了一種相對簡單的懸浮速度計算模型。該模型相比傳統懸浮速度計算方法更加簡潔，計算結果更接近試驗測量結果。試驗驗證發現：在計算片狀體最小懸浮速度時，本文提供的計算模型相比傳統方法關于不規則顆粒懸浮速度的計算方法具有明顯的優越性；但對尺寸較小的片狀體，其計算結果也存在較大誤差。

[1] 干方建，潘曉陽，胡開文. 煙草物料風力輸送速度的分析和研究[J].合肥工業大學學報，1999 ，22(2)：131-133.

[2] 彭建恩. 物料懸浮速度的研究[J].糧食科技與經濟，2001(4)：37.

[3] 張佳，莊衛東，陳彬. 農業物料懸浮速度試驗臺的研制[J]. 黑龍江八一農墾大學學報，1998，10(3)：56-59.

[4] 李學軍，陳嘉真. 茶葉在空氣流中的懸浮速度[J].茶葉科學，1987，7(1)：63-64.

[5] 譚子成. 關于顆粒懸浮速度概念的引申[J].通風除塵，1992(2)：20-21.

[6] 李愛平，汪春. 苜蓿段長度對干燥速度與懸浮速度影響的試驗[J]. 農業機械學報,2006 (8):169-171.

[7] 周作伸，劉貴富. 羽毛空氣動力學特性的試驗研究[J]. 農業機械學報,1989(1):48-52.

[8] 張繼成,陳海濤,紀文藝,等.大豆脫出物懸浮速度試驗研究[J].農機化研究，2013,35(4)：127-131.

[9] 王維，王婭妮.物料懸浮速度測試臺的設計與試驗研究[J].中國農機化學報，2016(6)：45-46.

[10] 須山啟介，清水浩.單一谷粒懸浮速度研究[J].糧食與飼料工業, 1984(2):265-269.

A Calculation Model for the Minimum Suspension Velocity of a Sheet

Yuan Chengyu, Wang Juan, Chen Zhishui, Liao Yulan

(college of mechanical and electrical engineering, Hainan University,Haikou 570228, China)

The minimum suspension velocity of the sheet bodies can be obtained by conventional theoretical calculations and experimental. In the paper, the author provided a computing model of sheet bodies’ minimum suspension velocity in the pressure drag area. and conducted a verification test in sugarcane leaves through the self-made test device. The result showed that the sugarcane leaves minimal suspension speed by traditional theoretical calculations is large difference with the results of experimental measurements, the maximum relative error was 97.3% and the minimum relative error is 39.4%; while the calculation result by this paper is small difference with the results of experimental measurements,the maximum relative error is 24.9% and the minimum relative error is 4.75%.

sheet body; minimum suspension velocity; mathematical model

2016-07-07

海南省自然科學基金項目(20163061)

袁成宇(1976-),男，湖南邵陽人，副教授，在職博士研究生，(E-mail)ycy@hainu.edu.cn。

S183

A

1003-188X(2017)08-0062-04