基于改進HHT的電壓閃變檢測*

倪良華，肖李俊，呂干云，歷馨

（南京工程學院電力工程學院，南京211167）

0 引 言

電網中分布式電源的大量接入以及各種非線性、沖擊性和波動性負荷的投入，加劇了電網中的電壓波動［1］，電網中的電壓閃變頻繁出現，給工業生產和社會生活造成嚴重影響。供用電企業都希望檢測到準確的電壓閃變參數，從而有針對性地加裝補償設備進行電壓閃變治理，以改善電能質量。

近年來，電壓波動和閃變檢測問題已逐漸成為研究熱點，IEC給出了衡量閃變強度值的檢測原理框圖，學者們根據框圖提出了多種計算短時閃變、長時閃變的計算方法，但這些方法不適用于時變電壓閃變信號的檢測。目前常用的閃變檢測方法主要有平方解調法、小波變換法［3］，FFT分解法［4］、Hilbert變換法和S變換法［2］等等。文獻［3］采用小波包分析與擬同步檢波的方法，雖可提取電壓閃變包絡、高頻細節以及突變時間，但如何選擇合適的小波基仍需進一步研究。文獻［4］采用FFT方法檢測閃變信號，但對于閃變頻率非FFT頻率分辨率整數倍的閃變信號，采用FFT方法會產生柵欄效應，從而影響結果的準確性。文獻［5］中使用Teager能量算子對電壓閃變信號進行辨識，此方法對低頻部分的閃變信號具有較高的辨識準確度，但對高頻部分閃變信號，辨識準確度卻較低。文獻［6］采用原子分解法檢測電壓閃變信號，其檢測參數的準確度較高，但是計算量大，運行時間較長。文獻［7］首先使用數學形態濾波將閃變信號中的諧波與噪聲等干擾信號濾除，然后采用Hilbert變換方法求出閃變包絡線。不過數學形態學的濾波效果受選取的結構元素以及形態濾波器結構的影響，且使用Hilbert變換方法不能直接得到閃變的參數。文獻［8］提出Prony與Hilbert相結合的方法，選擇基于Hilbert變換的算法對電壓波動信號進行檢測，引入擴展Prony算法估計出信號頻率參數，但抗噪能力不理想。文獻［9］采用HHT方法進行電壓閃變參數辨識，但該方法中的EMD存在著模態混疊以及端點飛翼現象，使得分解出的IMF分量不理想，嚴重影響了閃變參數檢測的準確度。

針對HHT算法中EMD分解出的IMF分量不理想而導致閃變參數檢測誤差較大的問題，基于四點插值細分算法與HHT算法，提出了改進HHT的電壓閃變檢測方法。通過借助四點插值細分算法“分裂”新的控制點供三次樣條插值擬合包絡線，優化了EMD的“篩選”過程。仿真結果表明，采用四點插值細分算法改進的HHT方法能夠有效降低噪聲的干擾，且對模態混疊問題有一定的抑制作用，提高了最終檢測出的閃變參數準確度。

1 電壓閃變信號的數學模型

電壓閃變分為周期與非周期性閃變，其中周期性電壓閃變對電力系統危害最大，所以主要研究周期性電壓閃變。

周期性電壓閃變信號可抽象地看成以工頻電壓為載波，受到電壓閃變分量為調幅波的調制，其數學形式為［10］：

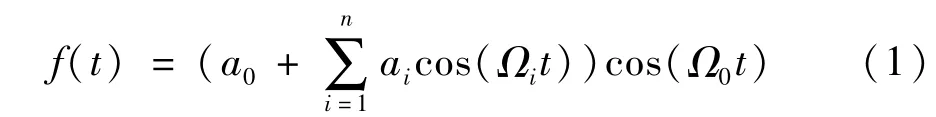
式中a0、Ω0分別是工頻載波電壓幅值及角頻率；而ai、Ωi分別是調幅波電壓的幅值及角頻率；Ωi的取值范圍為人對電壓波動的覺察范圍，一般取0.05 Hz～35 Hz。

2 HHT基本原理

HHT是一種信號處理方法，可以用于處理非平穩、非線性信號。該方法首先通過使用EMD將多分量信號分解為一組IMF分量，然后使用Hilbert變換對每個IMF分量進行分析處理，最終得到每個IMF分量的幅值與頻率［11］。

2.1 經驗模態分解

經驗模態分解（EMD）的本質是通過一系列計算，將一個非平穩非線性信號轉化為一組平穩的固有模態函數（IMF）分量。其中，每個IMF分量波形的上、下包絡線均值為零，且零點與極值點數目相等或者相差為1。EMD具體計算過程如圖1所示。

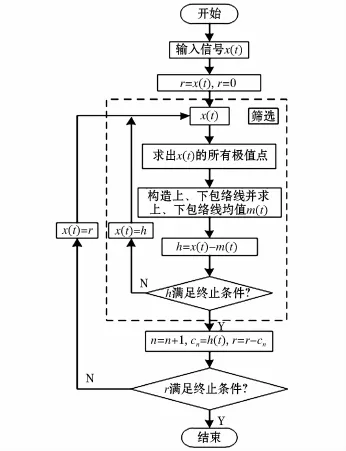
圖1 EMD分解流程圖Fig.1 Flow chart of EMD decomposition

從圖1中可以看出，EMD分解過程主要為虛線框中的“篩選”步驟。即先在原信號數據序列中找出所有的極大值點與極小值點，隨后使用三次樣條插值算法分別對極大值點和極小值點數據序列進行擬合，此時得到相應的上包絡線和下包絡線，接著求出上、下包絡線的均值，并用原信號數據序列減去它，從而得到一個新的信號數據序列，然后對產生的新的信號數據序列進行檢測，若發現新的信號數據序列不滿足IMF相關終止要求，則對該信號數據序列再進行一次“篩選”，直到滿足要求后再進行下一步計算。

2.2 Hilbert變換

對一連續的電壓閃變信號X（t），其Hilbert變換Y（t）為：

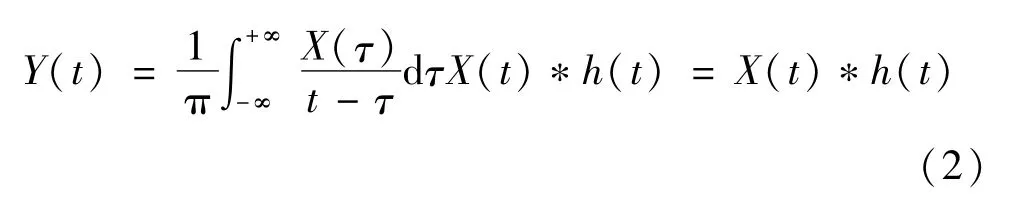
式中*表示卷積；t表示時間；τ表示積分分量。

電壓閃變信號 X（t）的幅值 a（t），相位 θ（t）以及瞬時頻率 f（t）可以通過式（3）～式（5）獲得：

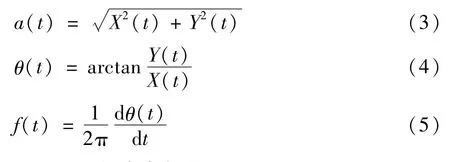
3 改進HHT閃變參數辨識原理

EMD在對閃變信號進行分解時，其中的“篩選”步驟產生的上、下包絡線存在著過包絡與欠包絡問題，甚至有時還存在著“過沖”現象［12］。這些情況的出現，降低了分解出的IMF分量理想程度，使得最終通過Hilbert變換檢測的閃變信號幅值和頻率誤差較大。

為此提出了一種改進HHT方法進行電壓閃變參數檢測，該方法主要是對EMD中的“篩選”步驟進行優化，即借助四點插值細分算法的“分裂”作用增加用于擬合上、下包絡線的控制點，繼而減緩了上、下包絡線的過包絡、欠包絡和“過沖”問題，分解的具體過程如圖2所示。通過此方法可以提升EMD分解的IMF分量的理想程度，并最終使閃變參數檢測準確度得到提高。

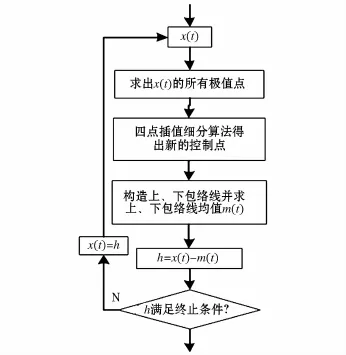
圖2 優化的EMD中“篩選”步驟流程圖Fig.2 Flow chart of“sifting”step in improved EMD

3.1 四點插值細分算法

四點插值細分算法是一種快速、離散的插值方法，該方法借助相鄰的四個控制點來計算新控制點，且每次“分裂”都使用相同的運算規則，屬于一種穩定的細分格式［13］。四點插值細分算法定義如下［14］。

根據下列細分規則，求出第k+1層的控制點。

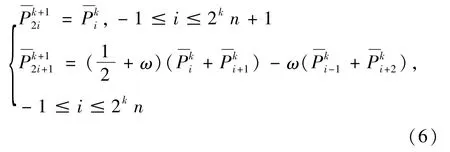
其中ω為張量參數，一般取其為1/16時，擁有最佳的Holder正則性。為使細分迭代層數可控，可對控制點的總個數進行限制，具體個數視實際情況而定。經過多次驗算，本文采用的四點插值細分算法“分裂”兩次時效果最好，因此迭代層數設為兩層。

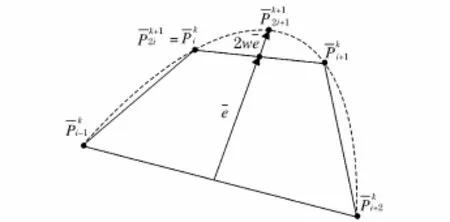
圖3 四點插值細分算法分裂圖Fig.3 Split chart of four point interpolation subdivision algorithm

從圖3中可以看出，第k+1層上的偶數序列的控制點為第k層上的舊控制點，而第k+1層上的奇數序列的控制點為第k層上相鄰的四個舊控制點依據相關運算規則而求出的，這種情況與式（6）相對應。

3.2 改進HHT閃變信號檢測

閃變信號在經過Hilbert變換處理后，分別得出工頻載波幅值A0與頻率f0以及去除直流分量的閃變包絡值A（t）；然后使用添加四點插值細分算法的EMD方法對閃變包絡信號進行分解，得到一組IMF分量；最后再次通過Hilbert變換求取每個IMF分量的幅值ai與頻率fi。具體流程如圖4所示。

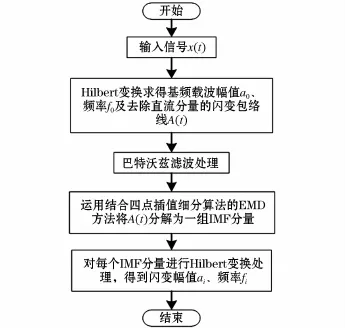
圖4 改進HHT電壓閃變參數檢測流程圖Fig.4 Flow chart of modified HHT detection method of voltage flicker

在運用優化的EMD分解過程中，求得極值點P0（x0，y0），P1（x1，y1），……Pn（xn，yn）（x0≤x1≤…≤xn，n≥5）后，令這些極值點為四點插值細分算法的初始控制點。隨后用式（6）所示的細分規則分裂出新的控制點 Pn+1（xn+1，yn+1），Pn+2（xn+2，yn+2），……，Pm（xm，ym），m≥6。接著對包含分裂出的新控制點在內的所有控制點使用三次樣條插值法進行擬合，并分別求出上、下包絡線。此種方法可以有效緩解提取包絡時出現的過包絡、欠包絡以及“過沖”問題，同時亦保留了三次樣條插值具有二階光滑度的優點［15］。

采用四點插值算法優化的EMD包絡線提取效果如圖5所示，從圖中可以看出，采用了四點插值算法優化的EMD產生的包絡線較之前未采用四點插值細分算法優化的EMD產生的包絡線更加光滑，且在局部區域有效地緩解了對信號的欠包絡、過包絡現象，從而提升了包絡的理想程度。

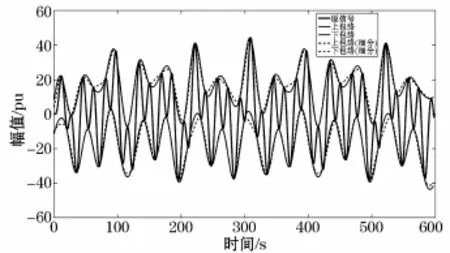
圖5 EMD提取包絡線對比示意圖Fig.5 Comparison chart of EMD extract envelop

4 仿真分析

4.1 含噪聲單一分量閃變信號

設信號表達式為：

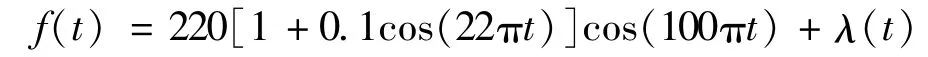
信號中工頻為50 Hz，調幅波頻率為11 Hz，幅值為基頻載波的0.1，同時在此信號基礎之上，又添加了信噪比為20 dB的高斯白噪聲。

首先使用Hilbert變換提取閃變信號包絡，得到工頻載波的頻率與幅值，結果如表1所示。隨后使用巴特沃茲濾波器對提取的調制分量包絡進行濾波，接著通過使用HHT方法與改進HHT方法分別對此信號進行檢測分析，得到結果如表2所示。在EMD分解過程中，采用四點插值細分算法而得的包絡線與未采用四點插值細分算法而得的包絡線對比情況如圖6所示。

表1 Hilbert變換辨識的工頻載波頻率和幅值Tab.1 Frequency and amplitude of power frequency carrier identification based on Hilbert transform

表2 含噪聲單一分量信號HHT與改進HHT檢測Tab.2 Detection of single component signal with noise between HHT and modified HHT

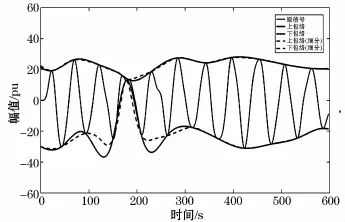
圖6 含噪聲單一分量信號包絡提取對比圖Fig.6 Comparison chart of envelop extraction in single component signal with noise

從圖6中可以看出，閃變信號成分較為簡單，信號波形分布基本均勻，采用四點插值細分算法提取的包絡線與未采用四點插值細分算法提取的包絡線總體上是吻合的，但由于信號中存在噪聲，因而圖中從左至右第四和第五個波峰分布異常，在這種情況下可以看到采用四點插值細分算法提取的包絡線較未采用四點插值細分算法提取的包絡線更為光滑，且在局部減緩了欠包絡與過包絡問題。

從表1中可以看出，使用Hilbert變換算法得到工頻頻率與幅值參數檢測準確度高，抗噪聲能力較好。從表2中可以看出，改進HHT方法檢測結果較未改進HHT方法檢測得出調幅波的頻率和幅值參數的誤差小。同時對比表1可以發現，兩種方法檢測出的調幅波參數誤差較表1都有一定升高，這是因為EMD分解過程受到了高斯白噪聲的影響，從而導致分解的IMF分量理想程度較低，然而改進HHT方法有效地降低了噪聲的干擾，提升了分解出的IMF分量的理想程度，從而使信號的頻率與幅值的檢測準確度得到提高。

4.2 多分量閃變信號

（1）不含噪聲

設信號表達式為：

f（t）=220［1+0.04cos（28πt）］+0.1cos（60πt）+λ（t）］cos（100πt）

信號中工頻為50 Hz，調幅波頻率為14 Hz，幅值為工頻載波的0.04，調幅波頻率為30 Hz，幅值為工頻載波的0.1。使用HHT方法與改進HHT方法的分別對此信號進行檢測，得出的結果如表3所示。

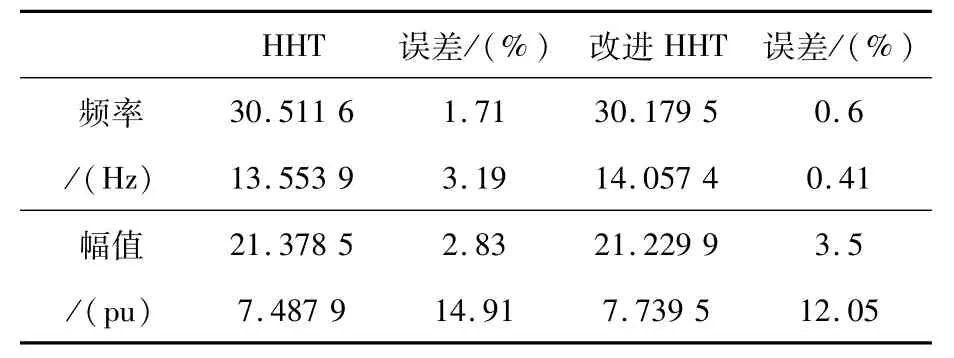
表3 多分量信號HHT與改進HHT檢測Tab.3 Detection of multi-component signals between HHT and modified HHT

其中，在EMD分解過程中，增加四點插值細分算法而得的包絡線與未增加四點插值細分算法而得的包絡線對比情況如圖7所示。

從圖7可以看出，閃變信號成分較為復雜，波形分布較圖6中的波形更為緊密。在相鄰波峰或波谷分布間隔較大的區域，采用四點插值細分算法提取的包絡線與未采用四點插值細分算法提取的包絡線基本吻合一致，但是在相鄰波峰或波谷分布間隔較小的區域，采用四點插值細分算法提取的包絡線較未采用四點插值細分算法提取的包絡線光滑度更好，且過包絡與欠包絡問題得到了緩解。

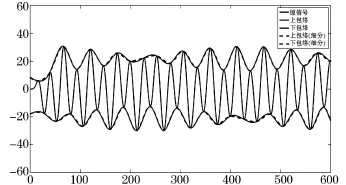
圖7 多分量信號包絡提取圖Fig.7 Chart of envelop extraction in multi-component signals

從表3中可以看出，在對多分量閃變信號檢測中，采用改進HHT算法的閃變頻率檢測準確度較未改進HHT算法的閃變頻率檢測準確度更高，優化效果明顯，而在對閃變幅值檢測時，在部分頻域具有優化效果。同時，通過對EMD分解IMF分量數目的統計，改進HHT分解的IMF分量個數為4個，而未改進HHT分解的IMF分量個數為7個。由此可以看出，改進HHT算法中的EMD分解可以有效緩解模態混疊問題。

（2）含噪聲

設信號表達式為：

f（t）=220［1+0.04cos（28πt）］+0.1cos（60πt）+λ（t）］cos（100πt）+λ（t）

該信號在多調制頻率信號基礎之上，添加了信噪比為20 dB的高斯白噪聲。在使用Hilbert變換提取包絡后，使用巴特沃茲濾波器進行濾波，隨后通過使用HHT與改進HHT算法分別對此信號進行解析，得到結果如表4所示。

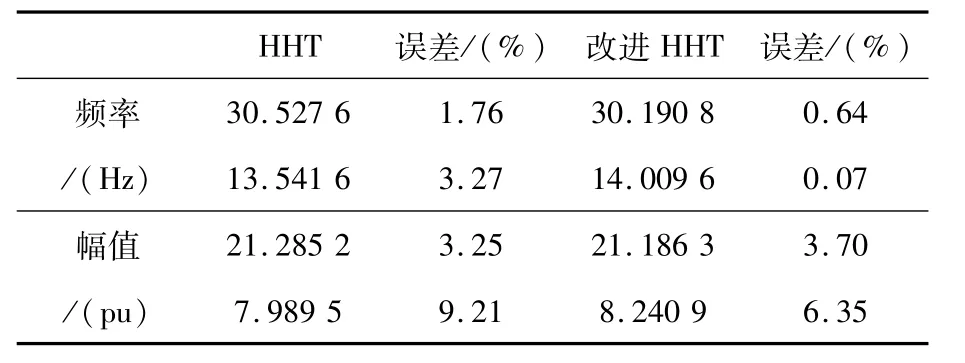
表4 多分量帶噪聲信號HHT與改進HHT檢測Tab.4 Detection of multi-component signals with noise between HHT and modified HHT

在EMD分解過程中，采用四點插值細分算法而得的包絡線與未采用四點插值細分算法而得的包絡線對比情況如圖8所示。

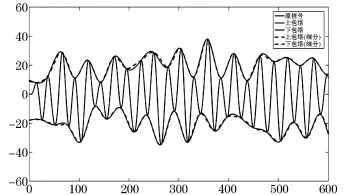
圖8 含噪聲多分量信號包絡提取圖Fig.8 Chart of envelop extraction in multi-component signals with noise

從圖8可以看出，由于閃變信號成分復雜且包含有噪聲分量，所以信號波形在局部波動較大。同時可以發現，采用四點插值細分算法與未采取四點插值細分算法提取的包絡線的區別與圖7類似。即在信號波形變化較為復雜的地方，采用四點插值細分算法提取的包絡光滑度更好，過包絡與欠包絡問題得到了緩解。

從表4可以看出，在對閃變頻率進行檢測時，采用改進HHT算法檢測的準確度與未采用改進HHT算法檢測的準確度更高，而對閃變幅值進行檢測時，改進HHT算法與未改進HHT算法相比，只在部分頻域上的檢測準確度出現提升。同時，通過對比表3與表4中的數據，發現閃變信號添加高斯白噪聲后，采用未改進HHT算法檢測閃變信號參數的準確度大部分出現了下降，而采用改進HHT算法的閃變信號參數檢測的準確度并未出現明顯變化。由此可得，改進HHT算法在對多分量閃變信號進行分析時，具有良好的抗噪能力。

5 結束語

針對應用HHT算法進行電壓閃變參數檢測過程中EMD分解出的IMF分量不理想而導致檢測準確度不高的問題，提出了一種采用四點插值細分算法對HHT進行改進的電壓閃變參數檢測方法。通過四點插值細分算法“分裂”更多的控制點供三次樣條插值算法擬合包絡線，使包絡線的過包絡與欠包絡問題得到緩解，優化了EMD的“篩選”過程，使EMD分解的IMF分量更加理想，從而最終提升了電壓閃變參數的檢測準確度。通過仿真計算，驗證了所提方法具有一定優越性。研究結果表明：采用改進HHT算法檢測電壓閃變信號，可以更有效地降低噪聲的干擾，對模態混疊具有一定的抑制作用。