基于改進PSO算法的VSC-HVDC控制器的優化設計

鄧旗，張英敏，李興源

（四川大學電氣信息學院，成都610065）

0 引 言

近年來隨著海上風電等新能源的大規模開發與接入，傳統的電力裝備、電網結構的運行技術等在接納新能源時顯得越來越力不從心［1］，柔性直流（VSCHVDC）輸電以其自身良好的動態無功支撐、潮流翻轉時直流電壓極性不變、可向弱交流電網以及無源網絡供電等優勢逐漸引起廣泛的關注［2-4］。

控制系統是直流輸電的核心，在VSC-HVDC系統中通常采用基于直接電流控制的雙閉環控制器，其中內環電流控制器的作用是實現電流的快速跟蹤；外環控制器實現系統有功功率和無功功率的解耦控制［5］。在目前投入的工程中，直流控制系統的控制器基本上選用的是PI控制器［6］，合適PI參數的選取與否將直接影響系統的動態響應特性和其穩定性。在工程實踐中，通常采用試湊法或經驗法來對PI參數進行調試，但是在調試的過程中對技巧和經驗的要求較高，并且調試后的參數也不一定能使系統的性能達到最優，這使得PI參數的優化成為控制器設計中的一個難點［7］。針對上述方法的不足，文獻［8］根據Bode圖求出在高壓直流輸電系統中滿足其穩定性要求的PI控制器的參數范圍，然后按照一定的步長對其進行劃分得到有限組的樣本集，再將樣本逐一帶入PSCAD/EMTDC中進行仿真并通過計算性能指標找到工程意義上的全局最優PI參數。但該方法依賴于步長的選擇，步長太大容易使尋優陷入局部最優，優化出來的參數可能不是全局最適合的，甚至找不到合適的穩定參數；步長太小劃分的樣本集較多，有利于系統全局的尋優，但是同時計算量以及存儲數據占用的空間大，該方法存在一定的局限性和盲目性。文獻［7，9］基于高壓直流輸電（HVDC）系統的等效傳遞函數模型，采用粒子群優化算法對系統控制器的參數進行了優化，通過對電流階躍響應的仿真結果驗證了所優化出來結果的有效性。文獻［10-11］通過Simplex算法對VSC-HVDC系統中控制器的參數進行了優化，得到了較為理性的效果。

針對以上方法的不足，文章首先以VSC-HVDC系統的數學模型為基礎，建立了VSC整流側定有功功率的小信號模型，進而推導出其內環電流的開環等效傳遞函數，基于PSO算法對外環PI參數進行了優化整定，為避免PSO算法過早的陷入局部最優解，在基本的PSO算法基礎上對權重的取值進行了改進，使其兼顧“全局的粗略探測”和“局部的精細挖掘”。最后通過仿真驗證了該算法的有效性。

1 VSC-HVDC控制系統的數學模型

以圖1所示的VSC-HVDC系統整流側定有功功率為例，其主要由換流變壓器、濾波器、相電抗器和直流電容組成，us為公共連接點（Point of Common Coupling，PCC）電壓，uc為換流器輸出的交流側電壓，Ps為交流系統與VSC交換的有功功率，Is為流入換流器的電流（以流入換流器為正），R為VSC功率損耗的等效電阻，L為總的等效電感包括換流電抗電感和變壓器電感。

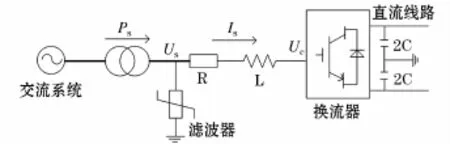
圖1 VSC整流側系統等效模型Fig.1 Equivalent model of VSC rectifier side system

以下將基于VSC直接電流控制，通過對整流側定有功功率控制的小信號建模推導出外環電流整定值的輸出到Ps這一過程的等效傳遞函數［12］。

1.1 VSC-HVDC系統的控制方式

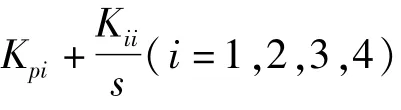
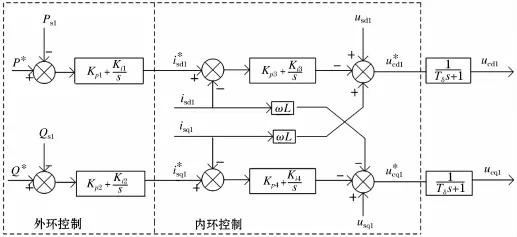
圖2 有功功率及無功功率控制器框圖（VSC1）Fig.2 Block diagram of active power and reactive power controller（VSC1）

1.2 內環電流控制器的小信號模型

如圖1所示，在以下研究中只考慮系統的基波分量，為了實現有功和無功的解耦控制，通常以PCC點電壓us為基準來構建同步旋轉坐標系［14-15］，其穩態數學模型為：

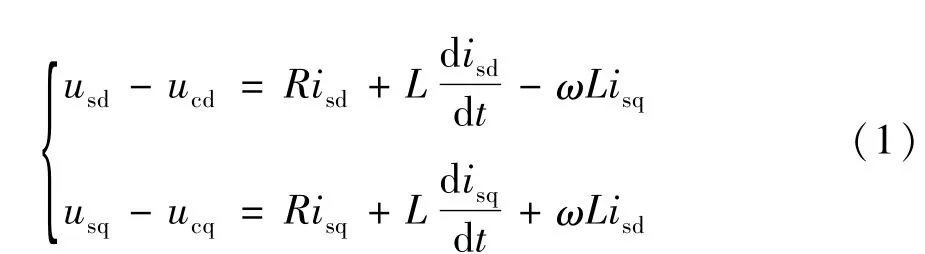
當系統在穩定點發生小擾動時，對式（1）進行線性化［16］并對其進行拉普拉斯變換可得：

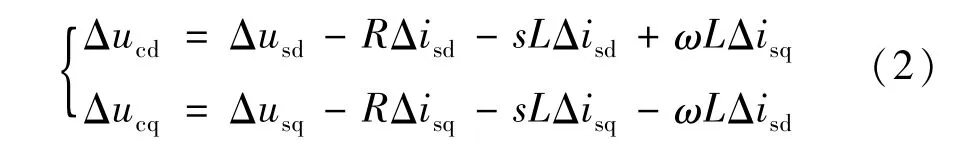
式中 usd、usq和 ucd、ucq分別為 PCC點電壓 us和VSC交流側電壓uc的d軸和q軸分量；isd、isq為流入換流器電流Is的d和q軸分量；ω為角頻率。

而在其內環電流控制器中：

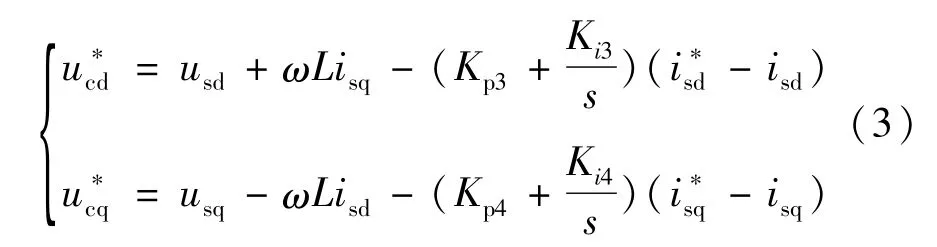
對式（3）進行線性化可得：

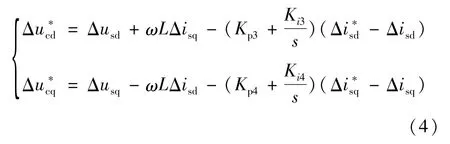
通常換流器具有一定的慣性，采用時間常數為Tδ的一階環節來模擬換流器的延時［17］，Tδ為換流器的開關周期，則：

對式（5）在穩定點附近線性化可得：

聯立式（2）、式（4）、式（6）可得：

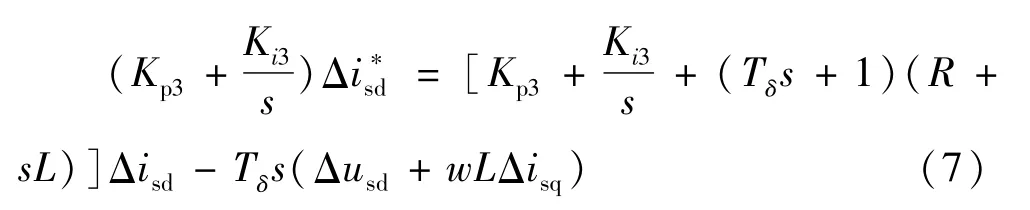
在本文中與VSC相連交流系統的短路比（Short-Circuit Ratio，SCR）較大，為強交流系統，并且以上的線性化是基于在穩定點附近進行的小擾動，因此Δusd≈0；通過對q軸的適當控制也可以使isq在穩態運行點保持不變［18］，從而 Δisq≈0；一般換流器的開關頻率較高，Tδ較小，所以在式（7）中項 Tδs（Δusd+wLΔisq）可等效為0。在此基礎上可得到內環控制的d軸電流的等效閉環傳遞函數：

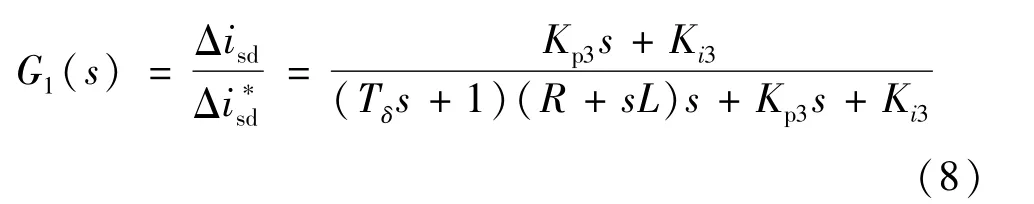
1.3 外環電壓控制器的小信號模型

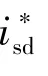
當以us為d軸的參考方向時，usq=0。在d-q軸同步旋轉坐標系下根據瞬時無功功率理論：

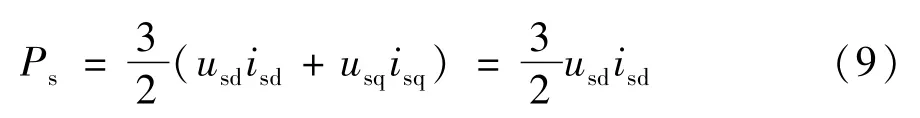
對式（9）線性化可得：

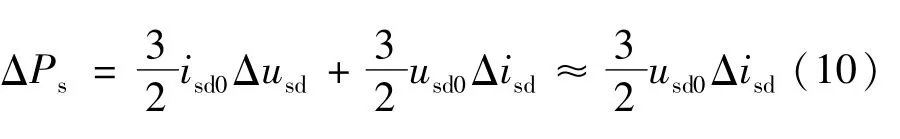
式中isd0、usd0下標含0的物理量代表其在穩態工作點的值。

由式（8）、式（10）可得：從內環輸入到交流系統與換流器交換的有功功率這一部分的等效開環傳遞函數為：

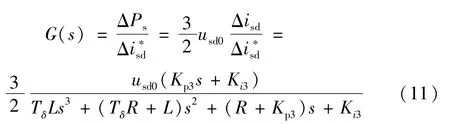
2 粒子群（PSO）優化算法

2.1 PSO算法的基本原理

粒子群優化（PSO）算法［19］是模擬鳥群覓食行為而發展起來的一種基于群體協作的隨機搜索算法，在該算法中每個粒子（也就是群體中的每只鳥）都代表所研究待優化問題的一個潛在的解，所有粒子都會由其待優化的函數決定的適應度值，其值大小的程度由目標函數的具體情況來決定應該選取最大值還是最小值。PSO算法首先會在可行解的空間中初始化一群粒子，該粒子的特征由速度、位置、適應度值三項指標來表示，在每一次迭代中，每個粒子通過追蹤自身個體極值Pbest和群體中極值Gbest來更新自己的位置和速度，并且在每一次更新后就要重新計算一次適應度值，通過比較新粒子的適應度值和個體極值、群體極值的適應度值來更新個體極值 Pbest和群體極值Gbest。

算法的流程：

（1）初始化：隨機產生 Size（粒子群規模）個粒子，隨機初始種群產生位置矩陣和速度矩陣；

（2）個體評價：將各個粒子的初始位置作為個體極值，計算每個粒子的適應值BestP，進而產生種群的最優位置以及目前群體的最優適應度值BestS；

（3）以下式來更新粒子的速度和位置，產生新的種群，每更新一次首先要檢查新粒子的速度和位置是否越界。

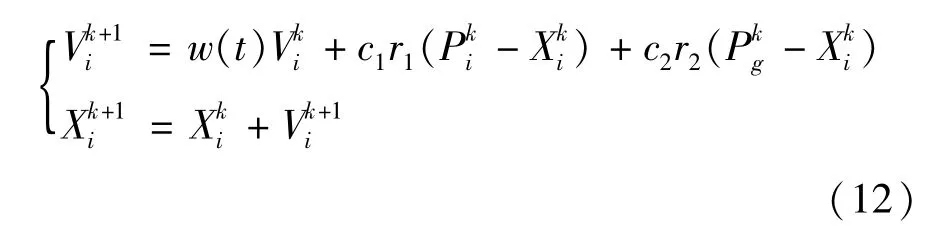
式中 k為當前迭代次數；i=1，2，…，Size；w（t）為慣性權重；Vi為粒子的速度；Xi為粒子的位置；Pi、Pg分別為粒子個體極值和種群極值；c1為局部學習因子，c2為全局學習因子，一般取c2的值要大一些；r1和r2為0-1的隨機數；

（4）比較新的粒子當前適應度值和自身歷史最優適應度值BestP，如果當前適應度值優于BestP，則該適應度值賦值給BestP，從而更新了該粒子的最優位置以及最優適應度值；同理也可用于比較當前適應度值和種群最優適應度值BestS；

（5）檢查結束條件（事先設定的最大迭代次數或計算精度），若滿足則結束尋優；否則k=k+1；轉至（3）繼續搜索。

2.2 PSO算法的改進

慣性權重w體現的是粒子繼承先前速度的能力，使得粒子保持運動慣性并逐步擴展搜索空間，能夠起到維護全局和局部搜索平衡的作用［20］。較大的慣性權重有利于算法全局的搜索，而一個相對較小的慣性權重則更有利于局部的搜索。為了能更好的平衡算法的全局搜索與局部搜索能力，在迭代的初期使w較大，從而保持算法有較強的全局搜索能力，隨著迭代的進行，使w逐漸變小以使算法在全局最優解附近進行更加精確的局部搜索，從而提高尋優的精度。本文以式（13）來定義慣性權重w：

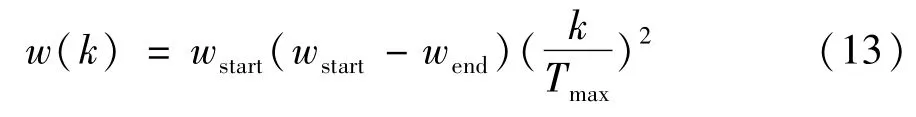
式中wstart為初始慣性權重；wend為迭代至最大次數時的慣性權重；k為當前的迭代次數；Tmax為最大迭代次數。在這里取經驗值wstart=0.9，wend=0.4。

2.3 在MATLAB中VSC-HVDC系統PI控制器參數優化的實現

PSO算法求解控制器的最優動態響應的前提是需要給出一個能表征系統性能指標的目標函數，在本文中以時間乘絕對誤差積分（Integral of time multiplied by the absolute value of error，ITAE）為尋優的性能指標函數，定義為：

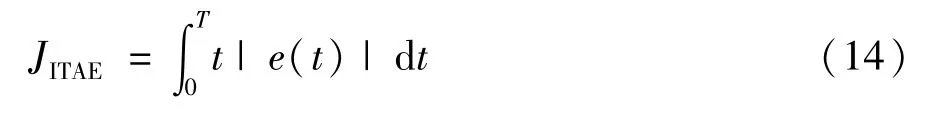
式中t為時間，T為仿真結束時間，對于VSCHVDC整流側定有功功率來說e（t）即為有功功率在動態調整過程中的實際輸出值與整定值的差值。該指標綜合考慮了穩態誤差與調節時間的關系，可使系統具有動態響應過程快速，超調量小，波動小等優點。基于該目標函數在MATLAB中進行控制器優化設計的流程圖如圖3所示。

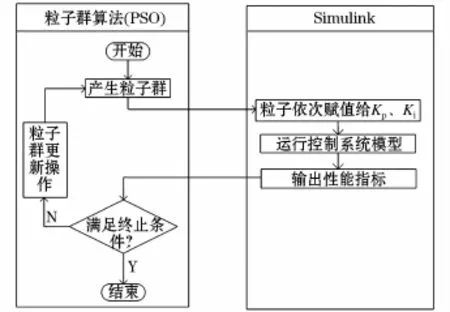
圖3 PSO優化PI控制器的過程示意圖Fig.3 Flow chart of optimizing PI controller with PSO

在圖3中，PSO將產生的粒子群（初始和更新后的種群）中的粒子依次賦值給PI控制器的參數Kp，Ki然后運行控制系統中的Simulink模型，得到該組參數對應的性能指標，其指標傳遞到PSO中作為該粒子的適應度值，最后判斷是否退出算法。

3 電磁暫態時域仿真分析

3.1 仿真中的直流系統

為了研究整流側定有功功率控制系統中外環PI控制器參數的優化，把在MATLAB中優化出來的控制器參數，輸入到數字仿真軟件PSCAD/EMTDC的模型中進行驗證所優化的有效性。在本文中所使用的模型為兩端的VSC-HVDC系統，左右兩端成對稱分布，其中換流器VSC1為整流站，采用定有功功率和定無功功率控制，VSC2為逆變站，如圖4所示。

圖4中的仿真參數：系統采用電壓源換流器，雙極運行；直流系統的額定電壓為±160 kV；換流器采用SPWM調制，其開關的頻率為1 980 Hz；整流側定有功功率為200 MW；兩側交流系統的頻率為工頻50 Hz；交流系統的額定電壓為220 kV；兩側連接變壓器的變比為220/160，其額定容量均為1 000 MVA；兩端的等效電阻R1、R2為1Ω；等效電感 L1、L2為0.072 4 H。

圖4 兩端VSC-HVDC系統結構Fig.4 System structure of two-terminal VSC-HVDC

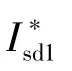
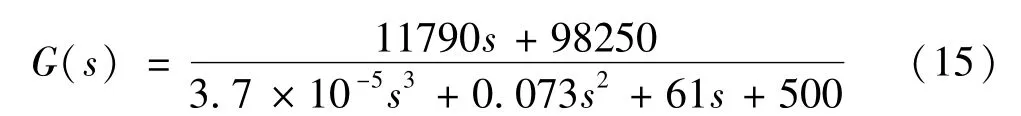
3.2 改進PSO算法整定PI控制器參數

由上述推導出的控制器傳遞函數G（s）以及以式（14）為優化目標的性能指標函數，可以在MATLAB中進行參數的尋優。在粒子群算法的程序中取c1為1.3，c2為1.7；粒子群的規模為100；最大迭代次數Tmax為100。本文中待優化的參數只有整流側定有功功率的外環PI參數Kp和Ki，其中在搜索時控制器參數 Kp的范圍為［0.03，1］；Ki的范圍為［1，100］，仿真時間設為20 s。

用粒子群算法按圖3所示的流程對控制器進行優化，經過100次的迭代，最終得到整流側定有功功率控制的最優PI參數為Kp=0.245 5，Ki=95.558 7，其性能指標JITAE=2.535 9×10-4。而初始系統外環的PI參數為Kp=0.05，Ki=50，其性能指標JITAE=4.207 7×10-4。優化前后的PI參數和性能指標值如表1所示。

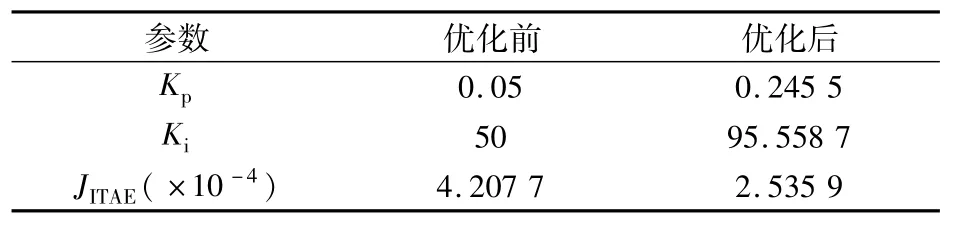
表1 優化前后的PI參數以及目標函數值的比較Tab.1 Comparison of PI parameters and objective function values before and after optimization

3.3 有功功率階躍響應的比較

為驗證優化后的PI參數的有效性，在1 s時將有功功率的整定值降低50 MW到150 MW，以觀察有功功率跟蹤其整定值的情況。圖5為在1 s時有功功率的整定值發生變化后在不同參數情況下所對應的階躍響應曲線。

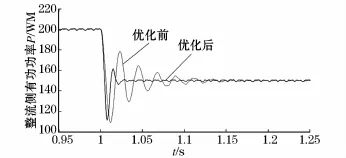
圖5 整流側有功功率階躍響應曲線（150 MW）Fig.5 Step response curve of the rectifier active power（150 MW）

仿真結果表明：用粒子群算法優化后得到的控制器參數，能夠使柔性直流輸電系統的有功功率整定值在發生階躍變化時快速的跟蹤其值，以滿足動態響應性能的要求。與原始PI參數相比，優化后的控制器參數使得振蕩周期從6個減小到2個，在暫態過程中系統的振蕩能量明顯降低，從而證明了用粒子群算法優化控制器參數的有效性。

3.4 最優PI控制器的魯棒性檢驗

為驗證這組最優控制器參數的魯棒性，使系統運行在不同的工作點，觀察有功功率的階躍響應特性的變化。在仿真開始前，取整流側定有功功率的原始整定值為100 MW，在1 s時使有功的整定值變為70 MW，圖6為有功整定值為100 MW時不同控制器參數所對應的階躍響應曲線。

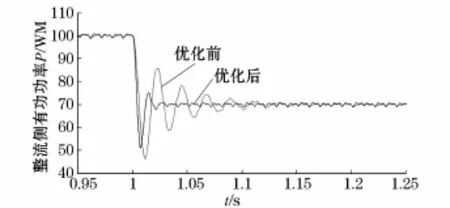
圖6 整流側有功功率階躍響應曲線（100 MW）Fig.6 Step response curve of the rectifier active power（100 MW）

圖6的仿真結果表明，優化出來的控制器參數在系統運行于不同的工作狀態時，對系統振蕩的首擺和后續擺動都有良好的阻尼作用，使震蕩幅值減小，穩定收斂的速度加快。

為了進一步驗證這組參數的魯棒性，取原始的有功功率的整定值為100 MW，在1 s時令潮流翻轉，即整流側有功功率的整定值由100 MW變為-100 MW，持續時間為0.5 s，圖7為系統潮流翻轉時，在不同參數狀態下的系統階躍響應曲線。

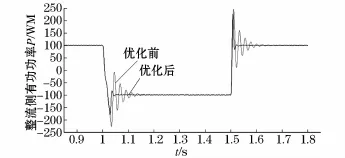
圖7 整流側有功功率階躍響應曲線（-100 MW）Fig.7 Step response curve of the rectifier active power（-100 MW）

由圖7的仿真結果可以得到，經過優化后的控制器參數，在系統潮流翻轉時，跟蹤整定值的速度加快，超調量減小，系統性能得到改善，測試結果表明采用優化后的PI控制器參數具有良好的魯棒性。

3.5 優化算法的性能對比

采用文獻［8］的傳統優化算法，對處于穩定運行區域內的可行解進行劃分，最終得出整流側定有功功率控制的最優PI參數為：Kp=0.18，Ki=58.27，其性能指標JITAE=3.641×10-4。從目標函數性能指標上可以看出文獻［8］的優化效果劣于本文所提改進粒子群算法。為了進一步驗證兩種優化算法的特性，對整流側有功功率的階躍響應進行了比較：在1 s時有功功率的整定值由200 MW減少到150 MW；在1 s時有功功率發生潮流翻轉，由100 MW變為-100 MW。其仿真結果如圖8所示。

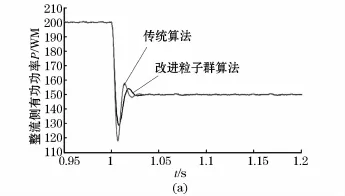
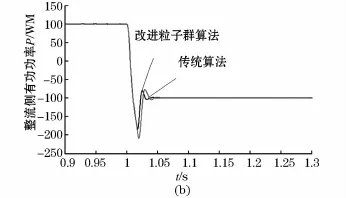
圖8 兩種算法下整流側有功功率階躍響應曲線Fig.8 Step response curve of the rectifier active power by two different algorithms

由圖8可知，文獻［8］中的傳統算法取得了較為理想的效果，但是與本文所提改進粒子群算法相比，其振蕩首擺的幅值較大，振蕩的能量也較高，控制的效果相對較差。

4 結束語

根據推導出的VSC-HVDC控制系統的內環電流等效傳遞函數的表達式，利用改進的PSO算法對控制系統的PI參數進行了優化，在PSCAD/EMTDC仿真環境下，對系統在不同運行狀態下進行了有功功率階躍響應的測試，得到以下結論：

（1）以VSC-HVDC系統的動態性能評價指標作為粒子群優化算法目標函數的控制器參數優化方法，其控制量與整定值有很好的契合度，系統動態性能得到很大的提高；

（2）與原始的PI參數相比，本文中的粒子群優化算法使系統的動態性能指標值JITAE降低了39.7%，系統的響應特性明顯提高了；

（3）優化出來的控制器參數具有良好的魯棒性，這為PI控制器參數的尋優提供了一種系統化的方法。