筆算開平方，你也來試試吧！

余中華

筆算開平方，你也來試試吧！

余中華

平時有同學會問：“不用平方根表和計算器，可不可以求出一個數的平方根呢？”我們先一起來研究一下，怎樣求？這里1156是四位數，所以它的算術平方根的整數部分是兩位數，且易觀察出其中的十位數是3.于是問題的關鍵在于：怎樣求出它的個位數a（設其個位數為a）.為此，我們從a所滿足的關系式來進行分析.

根據兩數和的平方公式，可以得到：

1156=（30+a）2

即1156=302+2×30a+a2，

所以1156-302=2×30a+a2，

即256=（3×20+a）a.

這就是說，a是這樣的一個正整數，它與“3×20”的和，再乘它本身，等于256.

為了便于求得a，可用下面的豎式來進行計算：

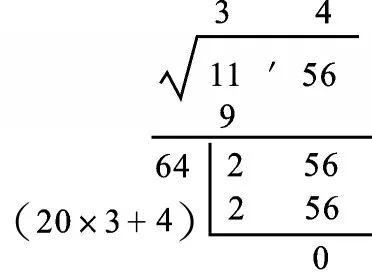
根號上面的數3是平方根的十位數.將256試除以“20×3”，得4.由于4與“20×3”的和為64，64與4的積等于256，4就是所求的個位數a.豎式中的余數是0，表示開方正好開盡.于是得到1156=342，或=34.

上述求平方根的方法，稱為筆算開平方法，用這個方法可以求出任何正數的算術平方根或其平方根的近似值，它的計算步驟如下：

1.將被開方數的整數部分從個位起向左每隔兩位劃為一段，用撇號分開（如豎式中的11＇56），分成幾段，表示所求平方根是幾位數；

2.根據左邊第一段里的數，求得平方根的最高位上的數（如豎式中的3）；

3.用第一段的數減去最高位上數的平方，在它們的差的右邊寫上第二段數組成第一個余數（豎式中的256）；

4.把求得的最高位數乘20去試除第一個余數，所得的最大整數作為試商（如“3×20”除256，所得的最大整數是4，即試商是4）；

5.用商的最高位數的20倍加上這個試商再乘以試商.如果所得的積小于或等于余數，試商就是平方根的第二位數；如果所得的積大于余數，就把試商減小再試［如豎式中（20×3+4）×4=256，說明試商4就是平方根的第二位數］；

6.用同樣的方法，繼續求平方根的其他各位上的數.

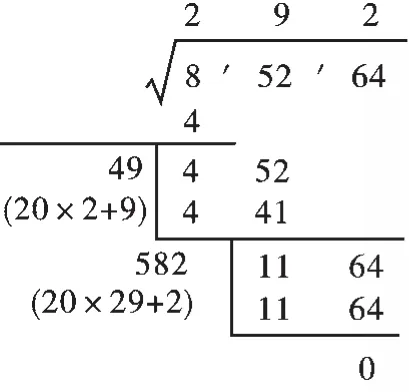
如遇開不盡的情況，可根據所要求的精確度求出它的近似值.例如求的近似值（精確到0.01），可列出下面的豎式，并根據這個豎式得到≈3.54.

筆算開平方運算較繁，在實際中直接應用較少，但用這個方法可求出一個正數的平方根的具有任意精確度的近似值.

我國古代數學的成就燦爛輝煌，早在公元前1世紀問世的我國經典數學著作《九章算術》里，就在世界數學史上第一次介紹了上述筆算開平方法.據史料記載，國外直到公元5世紀才有對于開平方法的介紹.

江蘇省海安縣墩頭鎮仇湖初級中學）