巖石非線性黏彈塑性蠕變模型研究

楊廣雨，王 偉，熊德發，馮曉偉

(1.河海大學 巖土力學與堤壩工程教育重點實驗室，江蘇 南京 210098；2.河海大學 巖土工程科學研究所，江蘇南京 210098)

巖石非線性黏彈塑性蠕變模型研究

楊廣雨1，2，王 偉1，2，熊德發1，2，馮曉偉1，2

(1.河海大學 巖土力學與堤壩工程教育重點實驗室，江蘇 南京 210098；2.河海大學 巖土工程科學研究所，江蘇南京 210098)

提出一種新的非定常粘滯系數的流變元件，然后將提出的非線性流變元件引進到Poyting-Thomson模型中，從而建立了新的非線性黏彈塑性流變模型，該模型不但可以較好地模擬巖石蠕變三個階段，而且模型參數較少。推導出模型的本構方程及蠕變方程，并探討了模型參數的辨識方法，最后利用本文建立的非線性流變模型所得到的理論曲線與砂巖蠕變試驗曲線進行對比分析。結果表明：本文建立的非線性流變模型具有較高的準確性及合理性。

巖石流變；非線性元件；加速蠕變；飽依丁-湯姆遜模型

巖石流變是影響巖土工程長期穩定性的一個重要因素，在對巖石流變現象的模擬方法中，利用彈簧、滑塊及黏性元件模擬巖石蠕變現象是較為常用的方法，但是傳統的基本元件都為線性元件，只能模擬巖石蠕變的前兩個階段，即衰減階段和穩定階段，無法模擬加速蠕變階段。因此，很多學者開始將非線性流變元件引入到現有的流變模型中去以便能模擬巖石加速蠕變階段[1-11]。本文針對傳統的Poyting-Thomson模型無法模擬巖石加速蠕變階段的不足，通過引進非定常黏滯系數的黏滯元件，建立了非線性流變模型，擬合結果表明本文建立的模型的正確性及可行性。

1 巖石非線性黏彈塑性流變模型

1.1 改進的非線性流變元件及模型本構關系

本文在熊良宵等[12]構建的非線性流變元件的基礎上通過改進提出一種新的非定常黏塑性元件，該元件中的黏滯系數是與流變時間t有關的函數，改進后的非線性流變元件示意圖見圖1。

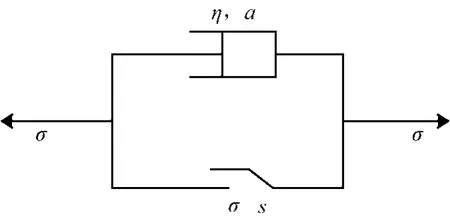
圖1 本文使用的非線性流變元件Fig.1 The non-linear rheological component

改進后的元件滿足以下應力-應變關系。

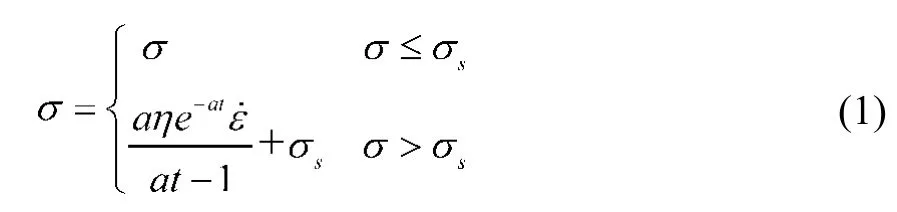
將上述改進后的流變元件（下圖2的第1部分）與傳統的飽依丁-湯姆遜體模型（下圖2的第2部分）進行串聯，從而可以得到新的非線性流變模型，見圖2。

圖2 本文建立的巖石非線性流變模型Fig.2 The nonlinear rheological model of rock

由于本文建立的模型的本構關系受到應力σs的影響，所以，需要根據應力σ與σs關系來建立模型的本構關系，由模型的性質可知，需要分兩種情況來建立模型的本構關系，第一種是當σ ≤ σs時，第二種情況是當σ ＞σs時。下面對這兩種情況分別推導其本構關系。

當σ ≤ σs時，此時由于滑塊受力小于摩擦阻力，滑塊無法滑動，因此圖2的第一部分應變為零，第一部分相當于一個剛體，對模型的本構關系沒有影響，此時模型就變成傳統的飽依丁-湯姆遜模型。

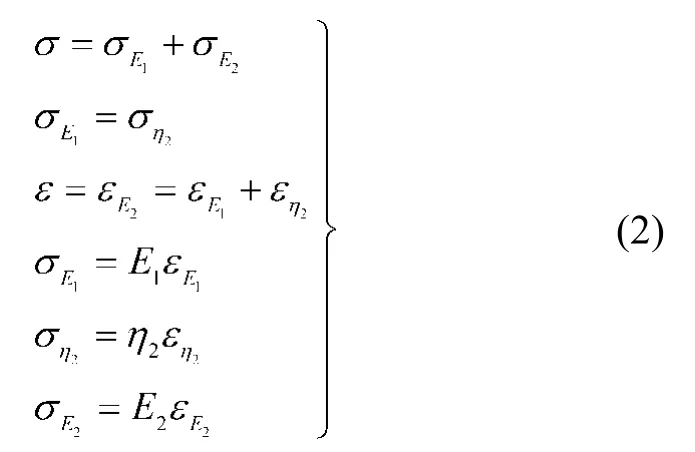
當σ ≤ σs時，模型的狀態方程為

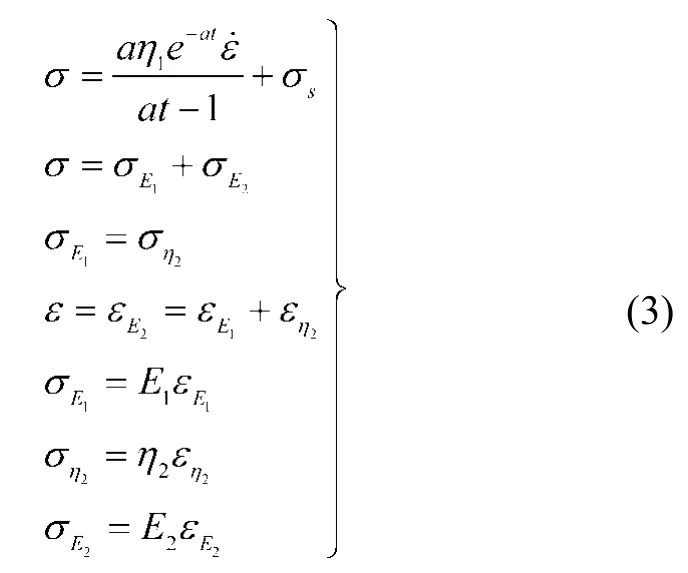
式中：σEi(i=1，2)為對應彈性元件所受的應力，εEi(i=1，2)為對應元件的應變，εηi(i=1，2)為模型中對應黏性元件的應變，σηi(i=1，2)為模型中對應黏性元件所受到的應力，ηi(i=1，2)為對應黏性元件的黏滯系數，ε時模型的應變，ε·為模型的應變率。

利用上述得到的(2)、(3)式，可以求得模型的本構關系。

當σ ≤ σs時，模型本構關系為

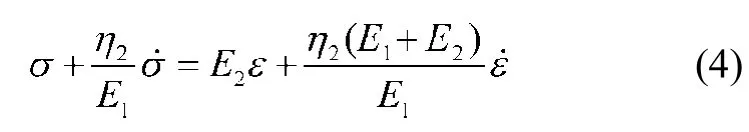
當σ ＞ σs時，模型的本構方程為

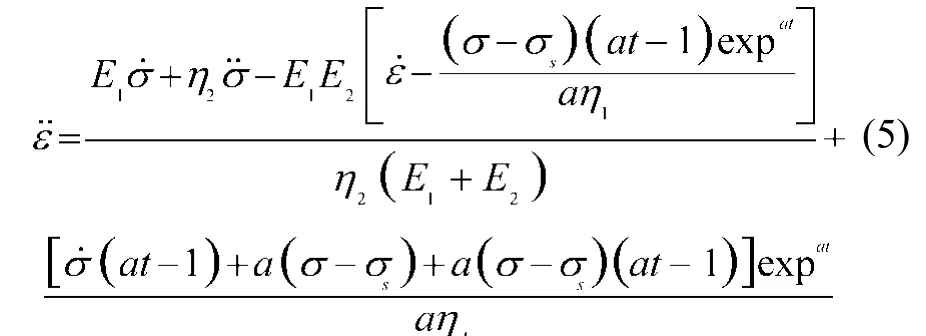
1.2 非線性流變模型蠕變特性分析

為了探究建立的模型具有哪些流變特性，首先需要建立σ =σ0時的巖石流變方程，根據兩式，利用Laplace變換求解方程時，首先需要求解當時間t=0時的初始條件。當t=0時，應力狀態不同時，初始條件也是有差別的。下面分別給出當時間t=0時σ ≤ σs與σ ＞ σs的初始條件。

當σ0≤ σs時，σ0為定常數，ε(0)為

當σ0＞ σs時，σ =0，σ¨=0，

根據上述初始條件結合式，利用Laplace變換和逆變換可以求得模型的蠕變方程。

當σ0≤ σs時，模型的蠕變方程為

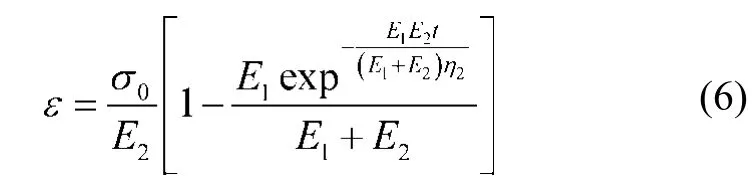
當σ0＞ σs時，模型的蠕變方程為

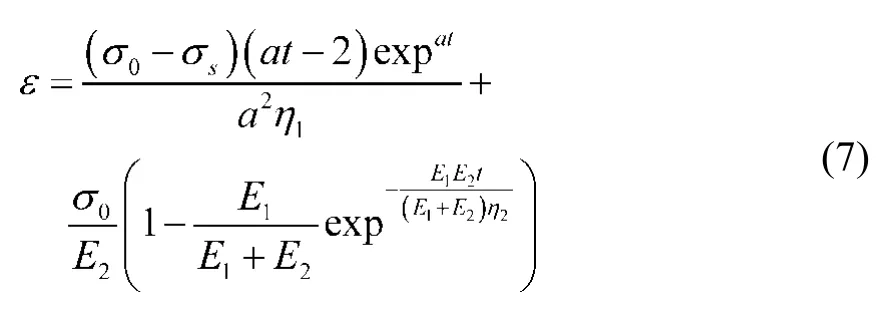
當σ0≤ σs時，上式模型的蠕變方程(6)對t求一階導數及二階導數，由此可得

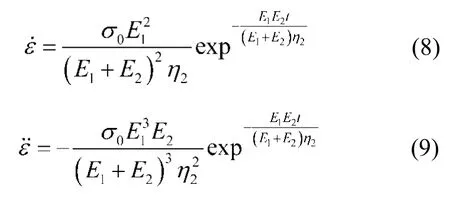
當σ0＞ σs時，上式模型的蠕變方程(7)對t求一階導數及二階導數，由此可得

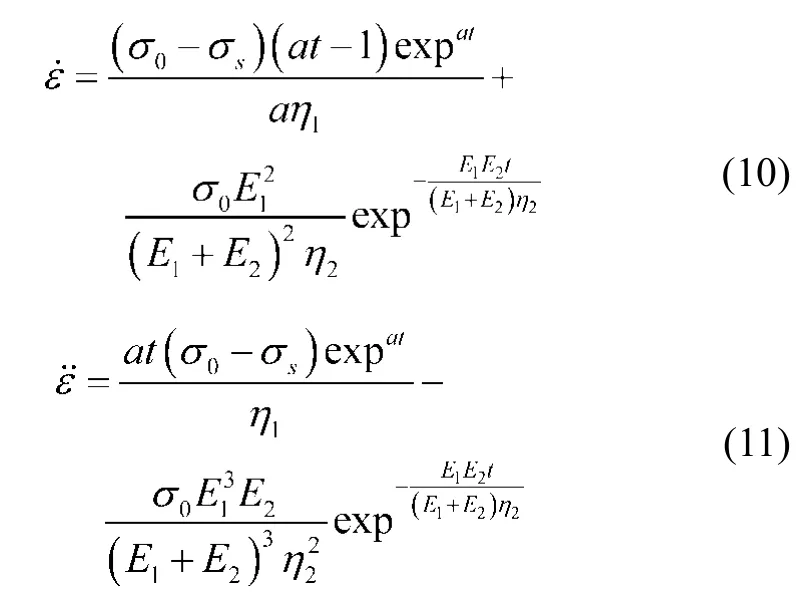
2 流變模型的試驗驗證

2.1 模型參數辨識方法

本文建立的非線性流變模型共有5個參數即E1、E2、η2、η1、a，這也是本文模型的一大優點。文中建立的流變模型可以按照有無加速蠕變階段的條件分為穩態蠕變（巖石蠕變只有前兩個階段）和不穩態蠕變（巖石應力超過σs，蠕變有三個階段），當模型為穩態蠕變時，采用最小二乘法進行參數擬合，參數擬合的效果往往較好。當巖石蠕變類型為不穩態蠕變時，直接用最小二乘法來參數擬合的效果往往不滿足要求。所以本文使用流變曲線分解法進行參數辨識，根據巖石試驗曲線的特點，辨識出加速蠕變的臨界時間tc，在tc之前，模型用最小二乘法求得模型中的E1、E2、η2、η1，然后用得到模型做出在tc之后的理論蠕變曲線，將巖石蠕變試驗曲線與得到的理論曲線做差得到差函數φ(t)，然后，將差函數φ(t)與時間t作冪指函數擬合，從而求得模型參數a，至此，模型中的全部參數均已求出。

2.2 模型驗證

本文是通過引用王偉等[12]砂巖流變試驗數據來驗證模型是否正確合理，該砂巖的分級加載流變試驗曲線見下圖3。

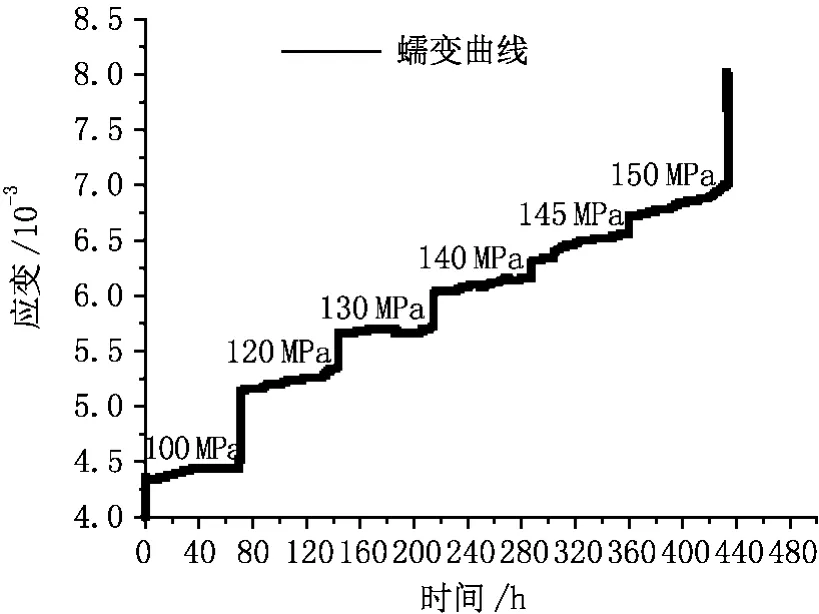
圖3 砂巖分級加載流變試驗曲線Fig.3 The rheological test curve in the conditon of sandstone graded load

根據圖3可知，當對砂巖施加第一級荷載時，砂巖產生了瞬時的彈性變形，在荷載小于150 MPa之前，在每一級荷載條件下，砂巖的應變率逐漸趨于一個大于零的定常值。當荷載大于150 MPa時，砂巖的應變率趨于無窮大，此時砂巖發生加速蠕變破壞。

在本文建立的非線性流變模型的基礎上，引進王偉等[13]砂巖流變試驗數據，當施加的荷載小于150 MPa時，利用最小二乘法進行模型參數辨識，當荷載大于等于150 MPa時，利用上節介紹的流變曲線分解法進行參數辨識。經過曲線擬合可得該模型在每級荷載條件下的參數，結果見表1。

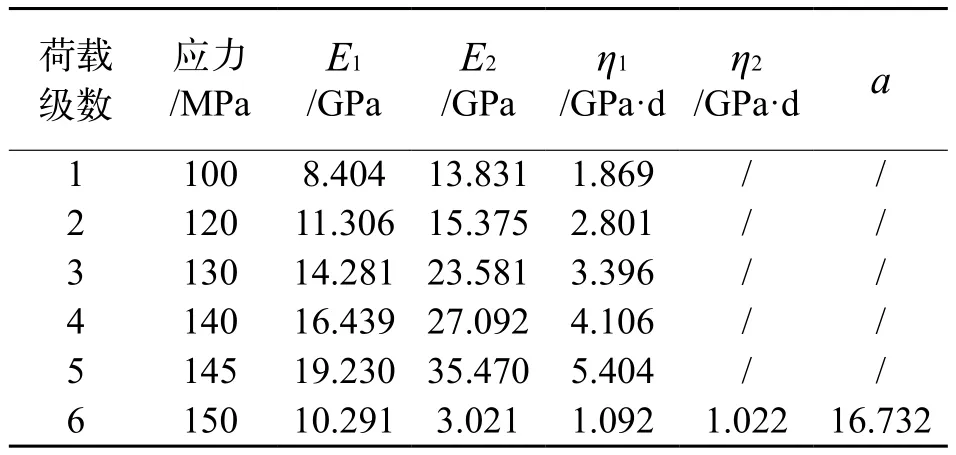
表1 流變模型參數擬合結果Tab.1 The parameter fi tting results for Rheological model

根據表1得到的模型參數，帶入到理論公式里，然后將理論流變曲線與砂巖流變試驗曲線進行對比分析，對比結果見下圖4。

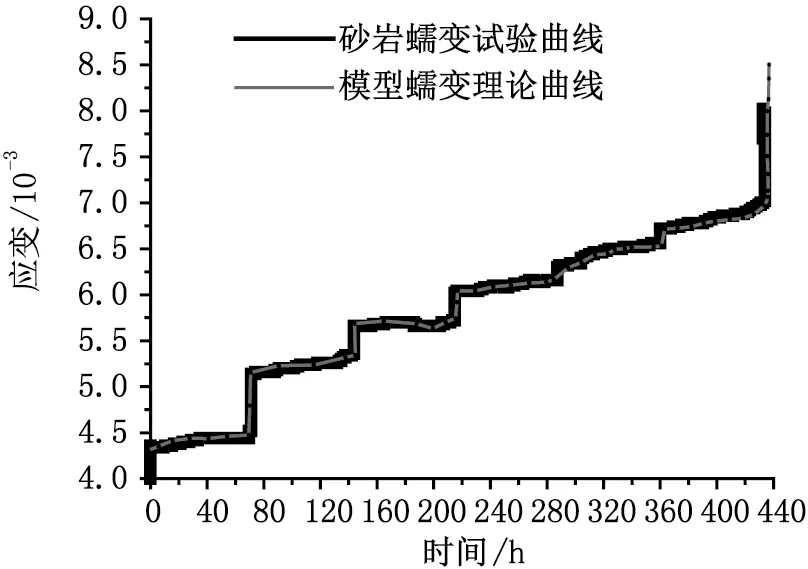
圖4 砂巖流變試驗曲線與模型理論曲線對比圖Fig.4 Comparison chart of rheological test curve and model theory curve of sandstone

根據圖4 的對比曲線可知本文建立的非線性流變模型不僅可以很好地反映巖石蠕變前兩個階段，也能夠較好地模擬巖石加速蠕變階段，從而證明了本文建立的非線性流變模型的正確性。

3 結論

1）使用改進的非線性流變元件，建立了新的飽依丁-湯姆遜模型，推導了其本構方程及蠕變方程，分析了流變模型的非線性流變特性，當σ0≤ σs時，本文建立的模型可以反映巖石蠕變的前兩個階段，當σ0＞σs時，非線性流變模型可以較好的模擬巖石蠕變全過程。

2）將模型得到的理論蠕變曲線與砂巖流變試驗曲線進行對比分析，兩者的曲線比較吻合，這表明了本文建立的非線性流變模型的正確性。

[1] 鄧榮貴，周德培，張倬元，等.一種新的巖石流變模型[J].巖石力學與工程學報，2001(6)：780-784.

[2] 康永剛，張秀娥.一種改進的巖石蠕變本構模型[J].巖土力學，2014(4)：1049-1055.

[3] 張樹光，王有濤，林曉楠.東梁煤礦非飽和砂巖黏彈塑性蠕變分析[J]. 遼寧工程技術大學學報：自然科學版，2017(2)：127-131.

[4] 曹樹剛，鮮學福.煤巖的廣義彈粘塑性模型分析[J].煤炭學報，2001(4)：364-369.

[5] 黃海峰，巨能攀，周 新，等.基于改進Burgers模型的片巖蠕變特性研究[J].水電能源科學，2017(3)：119-122.

[6] 胡 波，王宗林，梁 冰，等.巖石蠕變特性試驗研究[J].實驗力學，2015(4)：438-446.

[7] 劉東燕，趙寶云，朱可善，等.砂巖直接拉伸蠕變特性及Burgers模型的改進與應用[J].巖土工程學報，2011(11)：1740-1744.

[8] 蔣昱州，徐衛亞，王瑞紅.角閃斜長片麻巖流變力學特性研究[J].巖土力學，2011(Z1)：339-345.

[9] 韋立德，楊春和，徐衛亞.基于細觀力學的鹽巖蠕變損傷本構模型研究[J].巖石力學與工程學報，2005(23)：4253-4258.

[10] 蔡 煜，曹 平.基于Burgers模型考慮損傷的非定常巖石蠕變模型[J].巖土力學，2016，(Z2)：369-374.

[11] 張華賓，閔小東，張頃頃.基于Matlab的巖石蠕變模型參數辨識算法設計[J].河北工程大學學報：自然科學版，2016，33(3)：29-32.

[12] 熊良宵，楊林德，張 堯.巖石的非定常Burgers模型[J]. 中南大學學報：自然科學版，2010(2)：679-684.

[13] 王 偉，呂 軍，王海成，等.砂巖流變損傷模型研究及其工程應用[J].巖石力學與工程學報，2012(Z2)：3650-3658.

Study on nonlinear viscoelasto-plastic creep model of rock

YANG Guangyu1，2，WANG Wei1，2，XIONG Defa1，2，FENG Xiaowei1，2
(1.Key Laboratory of Ministry of Education For Geotechnical & embankment Engineering，Hohai University，Nanjing 210098，China；2.Geotechnical Research Institute，Hohai University，Nanjing 210098，China)

In this paper，a new rheological component with unsteady viscous coef fi cient is proposed，then connecting the proposed nonlinear rheological component with the Poyting-Thomson model，a new nonlinear viscoelastic-plastic rheological model is established. The model can not only simulate the three stages of rock creep，but also has less model parameters. In this paper，the constitutive equation and creep equation of the model are deduced，and the identi fi cation method of the model parameters is discussed. Finally，the theoretical curves obtained by the nonlinear rheological model established in this paper and the sandstone creep test curves is compared and analyzed. The results show that the nonlinear rheological model established in this paper has good accuracy and rationality.

rock rheology；nonlinear component；accelerative creep；Poyting-Thomson model

TU43

A

1673-9469（2017）04-0023-04

10.3969/j.issn.1673-9469.2017.04.006

2017-07-14

國家自然科學基金資助項目(11672343，51679069)；中央高校基本科研業務費專項資金資助項目(2016B20214)

楊廣雨(1993-)男，河南駐馬店人，碩士，從事巖石力學與工程方面的研究。